Octagram
| Regular octagram | |
|---|---|
 A regular octagram | |
| Type | Regular star polygon |
| Edges and vertices | 8 |
| Schläfli symbol | {8/3} t{4/3} |
| Coxeter–Dynkin diagrams | |
| Symmetry group | Dihedral (D8) |
| Internal angle (degrees) | 45° |
| Properties | star, cyclic, equilateral, isogonal, isotoxal |
| Dual polygon | self |
| Star polygons |
|---|
|
|
In geometry, an octagram is an eight-angled star polygon.
The name octagram combine a Greek numeral prefix, octa-, with the Greek suffix -gram. The -gram suffix derives from γραμμή (grammḗ) meaning "line".[1]
Detail[edit]

In general, an octagram is any self-intersecting octagon (8-sided polygon).
The regular octagram is labeled by the Schläfli symbol {8/3}, which means an 8-sided star, connected by every third point.
Variations[edit]
These variations have a lower dihedral, Dih4, symmetry:
 Narrow 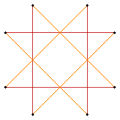 Wide (45 degree rotation) |
  Isotoxal |
 An old Flag of Chile contained this octagonal star geometry with edges removed (the Guñelve). |
 The regular octagonal star is very popular as a symbol of rowing clubs in the Cologne Lowland, as seen on the club flag of the Cologne Rowing Association. |
 The geometry can be adjusted so 3 edges cross at a single point, like the Auseklis symbol |
 An 8-point compass rose can be seen as an octagonal star, with 4 primary points, and 4 secondary points. |
The symbol Rub el Hizb is a Unicode glyph ۞ at U+06DE.
As a quasitruncated square[edit]
Deeper truncations of the square can produce isogonal (vertex-transitive) intermediate star polygon forms with equal spaced vertices and two edge lengths. A truncated square is an octagon, t{4}={8}. A quasitruncated square, inverted as {4/3}, is an octagram, t{4/3}={8/3}.[2]
The uniform star polyhedron stellated truncated hexahedron, t'{4,3}=t{4/3,3} has octagram faces constructed from the cube in this way. It may be considered for this reason as a three-dimensional analogue of the octagram.
| Regular | Quasiregular | Isogonal | Quasiregular |
|---|---|---|---|
 {4} |
 t{4}={8} |

|
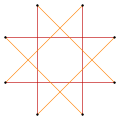 t'{4}=t{4/3}={8/3} |
| Regular | Uniform | Isogonal | Uniform |
 {4,3} |
 t{4,3} |

|
 t'{4,3}=t{4/3,3} |
Another three-dimensional version of the octagram is the nonconvex great rhombicuboctahedron (quasirhombicuboctahedron), which can be thought of as a quasicantellated (quasiexpanded) cube, t0,2{4/3,3}.
Star polygon compounds[edit]
There are two regular octagrammic star figures (compounds) of the form {8/k}, the first constructed as two squares {8/2}=2{4}, and second as four degenerate digons, {8/4}=4{2}. There are other isogonal and isotoxal compounds including rectangular and rhombic forms.
| Regular | Isogonal | Isotoxal | ||
|---|---|---|---|---|
 a{8}={8/2}=2{4} |
 {8/4}=4{2} |
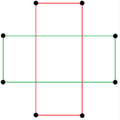
|
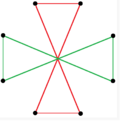
|
|
{8/2} or 2{4}, like Coxeter diagrams ![]()
![]()
![]() +
+ ![]()
![]()
![]() , can be seen as the 2D equivalent of the 3D compound of cube and octahedron,
, can be seen as the 2D equivalent of the 3D compound of cube and octahedron, ![]()
![]()
![]()
![]()
![]() +
+ ![]()
![]()
![]()
![]()
![]() , 4D compound of tesseract and 16-cell,
, 4D compound of tesseract and 16-cell, ![]()
![]()
![]()
![]()
![]()
![]()
![]() +
+ ![]()
![]()
![]()
![]()
![]()
![]()
![]() and 5D compound of 5-cube and 5-orthoplex; that is, the compound of a n-cube and cross-polytope in their respective dual positions.
and 5D compound of 5-cube and 5-orthoplex; that is, the compound of a n-cube and cross-polytope in their respective dual positions.
Other presentations of an octagonal star[edit]
An octagonal star can be seen as a concave hexadecagon, with internal intersecting geometry erased. It can also be dissected by radial lines.
| star polygon | Concave | Central dissections | ||
|---|---|---|---|---|
 Compound 2{4} |
 |8/2| |

|

|

|
 Regular {8/3} |
 |8/3| |

|

|

|
 Isogonal |

|

|

|

|
 Isotoxal |

|

|

|

|
Other uses[edit]

- The 8-pointed diffraction spikes of the star images from the James Webb Space Telescope are due to the diffraction caused by the hexagonal shape of the mirror sections and the struts holding the secondary mirror.[3]
- Used as a parol or star for the 2010 ABS-CBN Christmas Station ID Ngayong Pasko Magniningning Ang Pilipino (lit. 'This Christmas, the Filipinos will Shine') due to the usage of a sun from the Philippine flag, making it also a nationalism and patriotism-themed song aside from being a Christmas song.
See also[edit]
- Usage
- Rub el Hizb – Islamic character
- Star of Ishtar – symbol of the ancient Sumerian goddess Inanna and her East Semitic counterpart Ishtar and Roman Venus.
- Seshat – the hieroglyph of this ancient Egyptian goddess depicts a seven-petaled flower, forming an octagram with its stem.
- Star of Lakshmi – Indian character
- Surya Majapahit – usage during Majapahit times in Indonesia to represent the Hindu gods of the directions
- Compass rose – usage in compasses to represent the cardinal directions for the eight principal winds
- Auseklis – usage of regular octagram by Latvians
- Guñelve – representation of Venus in Mapuche iconography.
- Selburose – usage of regular octagram in Norwegian design
- Utu – ancient Mesopotamian god symbol and symbol of the Sun god
- Stars generally
- Others
References[edit]
- ^ γραμμή, Henry George Liddell, Robert Scott, A Greek-English Lexicon, on Perseus
- ^ The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History, (1994), Metamorphoses of polygons, Branko Grünbaum
- ^ Lawrence, Pete (13 September 2022). "Why do all the stars have 8 points in the James Webb images? An astronomer explains". BBC Science Focus Magazine. Retrieved 1 March 2023.
- Grünbaum, B. and G.C. Shephard; Tilings and patterns, New York: W. H. Freeman & Co., (1987), ISBN 0-7167-1193-1.
- Grünbaum, B.; Polyhedra with Hollow Faces, Proc of NATO-ASI Conference on Polytopes ... etc. (Toronto 1993), ed T. Bisztriczky et al., Kluwer Academic (1994) pp. 43–70.
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26. pp. 404: Regular star-polytopes Dimension 2)
