Function (mathematics): Difference between revisions
m →Developments prior to 1850: fix footnote error |
→Developments prior to 1850: vet, check what sources I have , split into "analysis" and "logic" , add De Morgan, split the analysis Boole out from the logical Boole |
||
| Line 222: | Line 222: | ||
The history of the function concept in mathematics is described by {{harvtxt|da Ponte|1992}} <ref> Another short but useful history is found in Eves 1990 pages 234-235 </ref>. The underlying idea of a function dates back to the [[Mathematics in medieval Islam|Persian mathematician]], [[Sharaf al-Dīn al-Tūsī]], in the 12th century. In his analysis of |
The history of the function concept in mathematics is described by {{harvtxt|da Ponte|1992}} <ref> Another short but useful history is found in Eves 1990 pages 234-235 </ref>. The underlying idea of a function dates back to the [[Mathematics in medieval Islam|Persian mathematician]], [[Sharaf al-Dīn al-Tūsī]], in the 12th century. In his analysis of |
||
the equation <math>x^3 + d = bx^2</math> for example, he begins by changing the equation's form to <math>x^2 (b - x) = d</math>. He then states that the question of whether the equation has a solution depends on whether or not the “function” on the left side reaches the value <math>d</math>. To determine this, he finds a [[Maxima and minima|maximum value]] for the function. Sharaf al-Din then states that if this value is less than <math>d</math>, there are no positive solutions; if it is equal to <math>d</math>, then there is one solution; and if it is greater than <math>d</math>, then there are two solutions.<ref>{{Citation|last=Victor J. Katz|first=Bill Barton|title=Stages in the History of Algebra with Implications for Teaching|journal=Educational Studies in Mathematics|publisher=[[Springer Science+Business Media|Springer Netherlands]]|volume=66|issue=2|date=October 2007|doi=10.1007/s10649-006-9023-7|pages=185–201 [192]}}</ref> |
the equation <math>x^3 + d = bx^2</math> for example, he begins by changing the equation's form to <math>x^2 (b - x) = d</math>. He then states that the question of whether the equation has a solution depends on whether or not the “function” on the left side reaches the value <math>d</math>. To determine this, he finds a [[Maxima and minima|maximum value]] for the function. Sharaf al-Din then states that if this value is less than <math>d</math>, there are no positive solutions; if it is equal to <math>d</math>, then there is one solution; and if it is greater than <math>d</math>, then there are two solutions.<ref>{{Citation|last=Victor J. Katz|first=Bill Barton|title=Stages in the History of Algebra with Implications for Teaching|journal=Educational Studies in Mathematics|publisher=[[Springer Science+Business Media|Springer Netherlands]]|volume=66|issue=2|date=October 2007|doi=10.1007/s10649-006-9023-7|pages=185–201 [192]}}</ref> |
||
==== The notion of "function" in analysis ==== |
|||
As a mathematical term, "'''function'''" was coined by [[Gottfried Leibniz]], in a 1673 letter, to describe a quantity related to a [[curve]], such as a curve's [[slope]] at a specific [[Point (geometry)|point]].<ref name="Thompson">Thompson, S.P; Gardner, M; ''Calculus Made Easy''. 1998. Page 10-11. ISBN 0312185480.</ref> <ref> Eves dates Leibniz's first use to the year 1694 and also similarly relates the usage to "as a term to denote any quantity connected with a curve, such as the coordinates of a point on the curve, the slope of the curve, and so on"(Eves 1990:234). </ref> The functions Leibniz considered are today called [[derivative|differentiable functions]]. For this type of function, one can talk about [[limit of a function|limit]]s and [[derivative]]s; both are measurements of the output or the change in the output as it depends on the input or the change in the input. Such functions are the basis of [[calculus]]. |
As a mathematical term, "'''function'''" was coined by [[Gottfried Leibniz]], in a 1673 letter, to describe a quantity related to a [[curve]], such as a curve's [[slope]] at a specific [[Point (geometry)|point]].<ref name="Thompson">Thompson, S.P; Gardner, M; ''Calculus Made Easy''. 1998. Page 10-11. ISBN 0312185480.</ref> <ref> Eves dates Leibniz's first use to the year 1694 and also similarly relates the usage to "as a term to denote any quantity connected with a curve, such as the coordinates of a point on the curve, the slope of the curve, and so on"(Eves 1990:234). </ref> The functions Leibniz considered are today called [[derivative|differentiable functions]]. For this type of function, one can talk about [[limit of a function|limit]]s and [[derivative]]s; both are measurements of the output or the change in the output as it depends on the input or the change in the input. Such functions are the basis of [[calculus]]. |
||
| Line 227: | Line 229: | ||
[[Johann Bernoulli]] had, "by 1718, had come to regard a function as any expression made up of a variable and some constants" <ref> Eves 1990:234</ref>, and [[Leonhard Euler]] during the mid-18th century used the word to describe an [[Expression (mathematics)|expression]] or [[formula]] involving variables and constants e.g. ''x''<sup>2</sup> + 3*''x'' + 2.<ref> Eves 1990:235 </ref> |
[[Johann Bernoulli]] had, "by 1718, had come to regard a function as any expression made up of a variable and some constants" <ref> Eves 1990:234</ref>, and [[Leonhard Euler]] during the mid-18th century used the word to describe an [[Expression (mathematics)|expression]] or [[formula]] involving variables and constants e.g. ''x''<sup>2</sup> + 3*''x'' + 2.<ref> Eves 1990:235 </ref> |
||
[[Alexis Claude Clairaut]] (in approximately 1734) and Euler introduced the familiar notation " f(x) ".<ref> Eves 1990:235 </ref> |
[[Alexis Claude Clairaut]] (in approximately 1734) and Euler introduced the familiar notation " f(x) ".<ref> Eves 1990:235 </ref> |
||
| ⚫ | |||
At first, the idea of a function was rather limited. [[Joseph Fourier]], for example, claimed that every function had a [[Fourier series]], something no mathematician would claim today. By broadening the definition of functions, mathematicians were able to study "strange" mathematical objects such as continuous functions that are [[nowhere differentiable]]. These functions were first thought to be only theoretical curiosities, and they were collectively called "monsters" as late as the turn of the 20th century. However, powerful techniques from [[functional analysis]] have shown that these functions are, in a precise sense, more common than differentiable functions. Such functions have since been applied to the modeling of physical phenomena such as [[Brownian motion]]. |
At first, the idea of a function was rather limited. [[Joseph Fourier]], for example, claimed that every function had a [[Fourier series]], something no mathematician would claim today. By broadening the definition of functions, mathematicians were able to study "strange" mathematical objects such as continuous functions that are [[nowhere differentiable]]. These functions were first thought to be only theoretical curiosities, and they were collectively called "monsters" as late as the turn of the 20th century. However, powerful techniques from [[functional analysis]] have shown that these functions are, in a precise sense, more common than differentiable functions. Such functions have since been applied to the modeling of physical phenomena such as [[Brownian motion]]. |
||
| ⚫ | |||
| ⚫ | |||
| ⚫ | :"That quantity whose variation is uniform . . . is called the independent variable. That quantity whose variation is referred to the variation of the former is said to be a ''function'' of it. The Differential calculus enables us in every case to pass from the function to the limit. This it does by a certain Operation. But in the very Idea of an Operation is . . . the idea of an inverse operation. To effect that inverse operation in the present instance is the business of the Int[egral] Calculus." |
||
[[Johann Peter Gustav Lejeune Dirichlet|Dirichlet]]<ref> Eves asserts that Dirichlet "arrived at the following formulation: "[The notion of] a ''variable'' |
[[Johann Peter Gustav Lejeune Dirichlet|Dirichlet]] and [[Nikolai Ivanovich Lobachevsky|Lobachevsky]] are traditionally credited with independently giving the modern "formal" definition of a function as a [[relation (mathematics)|relation]] in which every first element has a unique second element. Eves asserts that "the student of mathematics usually meets the Dirichlet definition of function in his introductory course in calculus<ref> Eves asserts that Dirichlet "arrived at the following formulation: "[The notion of] a ''variable'' is a symbol that represents any one of a set of numbers; if two variables ''x'' and ''y'' are so related that whenever a value is assigned to ''x'' there is automatically assigned, by some rule or correspondence, a value to ''y'', then we say ''y'' is a (single-valued) ''function'' of x. The variable ''x'' . . . is called the ''independent variable'' and the variable ''y'' is called the dependent variable. The permissible values that ''x'' may assume constitute the ''domain of definition'' of the function, and the values taken on by y constitute the ''range of values'' of the function . . . it stresses the basic idea of a relationship between two sets of numbers" Eves 1990:235.</ref>, but Dirichlet's claim to this formalization is disputed by [[Imre Lakatos]]: |
||
:There is no such definition in Dirichlet's works at all. But there is ample evidence that he had no idea of this concept. In his <nowiki>[1837]</nowiki>, for instance, when he discusses piecewise continuous functions, he says that at points of discontinuity the function ''has two values'': ... |
:There is no such definition in Dirichlet's works at all. But there is ample evidence that he had no idea of this concept. In his <nowiki>[1837]</nowiki>, for instance, when he discusses piecewise continuous functions, he says that at points of discontinuity the function ''has two values'': ... |
||
:(''Proofs and Refutations'', 151, Cambridge University Press 1976.) |
:(''Proofs and Refutations'', 151, Cambridge University Press 1976.) |
||
| ⚫ | |||
| ⚫ | :"That quantity whose variation is uniform . . . is called the independent variable. That quantity whose variation is referred to the variation of the former is said to be a ''function'' of it. The Differential calculus enables us in every case to pass from the function to the limit. This it does by a certain Operation. But in the very Idea of an Operation is . . . the idea of an inverse operation. To effect that inverse operation in the present instance is the business of the Int[egral] Calculus."<ref> Boole circa 1849 ''Elementary Treatise on Logic not mathematical including philosophy of mathematical reasoning'' in Grattan-Guiness and Bornet 1997:40</ref>. |
||
==== The logician's "function" ==== |
|||
[[Logician]]s of this time were primarily involved with analyzing [[syllogism]]s (the 2000 year-old Aristotelian forms and otherwise), or as [[Augustus De Morgan]] (1847) stated it: "the examination of that part of reafoning which depends upon the manner in which inferences are formed, |
|||
and the inveftigation of general maxims and rules for conftructing arguments [sic: archaic]"<ref>De Morgan 1847:1</ref>. At this time the notion of (logical) "function" is not explicit, but at least in the work of De Morgan and [[George Boole]] it is implied: we see abstraction of the argument forms, the introduction of variables, the introduction of a symbolic algebra, and some of the notions of set theory. |
|||
De Morgan's 1847 "FORMAL LOGIC OR, The Calculus of Inference, Neceffary [sic] and Probable" observes that "[a] logical truth depends upon the ''ftructure of the ftatement'', and not upon the particular matters fpoken of"; he wastes no time (preface page i) abstracting: "In the form of the propofition, the copula is made as abfract as the terms". He immediately (p. 1) casts what he calls "the proposition" (present-day propositonal ''function'') into a form such as "X is Y", where the symbols X, "is", and Y represent, respectively, the ''subject'', ''copula'', and ''predicate.'' While the word "function" does not appear, the abstraction is there, "variables" are there, the notion of inclusion in his symbolism “all of the Δ is in the О” (p. 9), and lastly a new symbolism for logical analysis, for example: |
|||
:" A<sub>1</sub> X)Y To take an X it is necessary to take a Y" [or To be an X it is necessary to be a Y] |
|||
:" A<sup>1</sup> Y)X To take an Y it is sufficient to take a X" [or To be a Y it is sufficient to be an X], etc. |
|||
In his 1848 ''The Nature of Logic'' Boole asserts that "logic . . . is in a more especial sense the science of reasoning by signs", and he briefly discusses the notions of "belonging to" and "class": "An individual may possess a great variety of attributes and thus belonging to a great variety of different classes" <ref> Boole 1848 in Grattan-Guiness and Bornet 1997:1, 2</ref>. Like De Morgan he uses the notion of "varible" drawn from analysis; he gives an example of "represent[ing] the class oxen by ''x'' and that of horses by ''y'' and the conjunction ''and'' by the sign + . . . we might represent the aggregate class oxen and horses by ''x + y''" |
|||
=== The logicist's "function": Development of the notion of "function" in logic 1850-1950 === |
=== The logicist's "function": Development of the notion of "function" in logic 1850-1950 === |
||
Revision as of 15:00, 12 August 2009
The mathematical concept of a function expresses the intuitive idea that one quantity (the argument of the function, also known as the input) completely determines another quantity (the value, or output). A function associates a unique value to each input of a specified type. The argument and value may be real numbers, but they can also be elements from any given sets: the domain and codomain of the function. In addition to elementary functions on numbers, functions include maps between algebraic structures such as groups, and maps between geometric objects such as manifolds.
There are many ways to represent or visualize functions: a function may be described by a formula, by a plot or graph, by an algorithm that computes it, or by a description of its properties. Sometimes, a function is described through its relationship to other functions (for example, inverse functions). In applied disciplines, functions are frequently specified by tables of values or by formulas. In pure mathematics, functions are defined using set theory, and there are theorems that show the existence of uncountably many different functions, most of which cannot be expressed with a formula or algorithm.
In a setting where outputs of functions are numbers, functions may be added and multiplied, yielding new functions. Collections of functions with certain properties, such as continuous functions and differentiable functions, usually closed under certain operations, are called function spaces and are studied as objects in their own right in real analysis. An important operation on functions, that distinguishes them from numbers, is composition of functions. The composite function is obtained by using the output of one function as the input of another. This operation provides the theory of functions with its most powerful structure.
Overview
Because functions are so widely used, many traditions have grown up around their use. The symbol for the input to a function is often called the independent variable or argument and is often represented by the letter x or, if the input is a particular time, by the letter t. The symbol for the output is called the dependent variable or value and is often represented by the letter y. The function itself is most often called f, and thus the notation y = f(x) indicates that a function named f has an input named x and an output named y.
The set of all permitted inputs to a given function is called the domain of the function. The set of all resulting outputs is called the image or range of the function. The range is often a subset of some larger set, called the codomain of a function. Thus, for example, the function f(x) = x2 could take as its domain the set of all real numbers, as its image the set of all non-negative real numbers, and as its codomain the set of all real numbers. In that case, we would describe f as a real-valued function of a real variable.
It is a usual practice in mathematics to introduce functions with temporary names like ƒ; we might define a function by ƒ(x) = 2x+1, which implies ƒ(3) = 7. When a name for the function is not needed, the form y = 2x+1 may be used.
If we use a function often, we may give it a more permanent name as, for example,
Functions need not act on numbers: the domain and codomain of a function may be arbitrary sets. One example of a function that acts on non-numeric inputs takes English words as inputs and returns the first letter of the input word as output. Furthermore, functions need not be described by any expression, rule or algorithm: indeed, in some cases it may be impossible to define such a rule. For example, the association between inputs and outputs in a choice function will often lack any fixed rule, although each input element is still associated to one and only one output.
A function of two or more variables is considered in formal mathematics as having a domain consisting of ordered pairs or tuples of the argument values. For example Sum(x,y) = x+y operating on integers is the function Sum with a domain consisting of pairs of integers. Sum then has a domain consisting of elements like (3,4), a codomain of integers, and an association between the two which can be described by a set of ordered pairs like ((3,4), 7). Evaluating Sum(3,4) then gives the value 7 associated with the pair (3,4).
Mathematical definition
One precise, mathematical definition of a function is that it consists of an ordered triple of sets, which may be written as . The first set is the domain of the function, the second set is the codomain of the function, and the third set is a set of ordered pairs. In each of these ordered pairs , the first element a in each ordered pair is from the domain, the second element b is from the codomain, and every element in the domain is the first element in one and only one ordered pair. The set of all second elements in the ordered pairs is known as the image of the function. Some authors use the term "range" to mean the image, others to mean the codomain.
For example, the function defined by f(x) = x2 is, to a mathematician, three sets. The domain is (usually) the real numbers, the codomain is also the real numbers, and the ordered pairs include such pairs as (3, 9).
The notation ƒ:X→Y indicates that ƒ is a function with domain X and codomain Y.
In most practical situations, the domain and range are understood from context, and only relationship between the input and output is given. Thus
is written simply as
The graph of a function is its set of ordered pairs. Such a set can be plotted on a pair of coordinate axes. The point (3, 9) can be plotted as a point three units to the right of the origin and nine units above the horizontal axis.
A function is a special case of a more general mathematical concept, a relation, for which the restriction that each element of the domain appear as the first element in one and only one ordered pair is removed. A relation is "single-valued" when for each element of the domain set, the graph contains at most one ordered pair (and possibly none) with it as a first element. A relation is called "total" when for each element of the domain, the graph contains at least one ordered pair with it as a first element (and possibly more than one). A relation which is both total and single-valued is a function.
In some parts of mathematics, including recursion theory and functional analysis, it is convenient to study partial functions in which some values of the domain have no association in the graph; i.e. single-valued relations. For example, the formula f(x) = 1/x does not define a value for x = 0, and so this formula only defines a partial function from the real line to the real line. The term total function, a synonym for function, can be used to stress the fact that every element of the domain does appear as the first element of an ordered pair in the graph. In other parts of mathematics, relations which are not single-valued are similarly conflated with functions: these are known as multivalued functions, with the corresponding term single-valued function for ordinary functions.
Some authors (especially in set theory) define a function as simply its graph f, with the restriction that the graph should not contain two distinct ordered pairs with the same first element. Indeed, given such a graph, one can construct a suitable triple by taking the set of all first elements as the domain and the set of all second elements as the codomain: this automatically causes the function to be total and surjective (see below). However, most authors in advanced mathematics outside of set theory prefer the greater power of expression afforded by the triple of sets (X,Y,f).
Many operations in set theory, for example the power set, have the class of all sets as their domain, therefore—although they are informally described as functions—they do not fit the above set-theoretical definition.
Vocabulary
A specific input in a function is called an argument of the function. For each argument value x, the corresponding unique y in the codomain is called the function value at x, output of ƒ for an argument x, or the image of x under ƒ. The image of x may be written as ƒ(x) or as y.
The graph of a function ƒ is the set of all ordered pairs (x, ƒ(x)), for all x in the domain X. If X and Y are subsets of R, the real numbers, then this definition coincides with the familiar sense of "graph" as a picture or plot of the function, with the ordered pairs being the Cartesian coordinates of points.
Notation
Formal description of a function typically involves the function's name, its domain, its codomain, and a rule of correspondence. Thus we frequently see a two-part notation, an example being
where the first part is read:
- "ƒ is a function from N to R" (one often writes informally "Let ƒ: X → Y" to mean "Let ƒ be a function from X to Y"), or
- "ƒ is a function on N into R", or
- "ƒ is an R-valued function of an N-valued variable",
and the second part is read:
- maps to
Here the function named "ƒ" has the natural numbers as domain, the real numbers as codomain, and maps n to itself divided by π. Less formally, this long form might be abbreviated
though with some loss of information; we no longer are explicitly given the domain and codomain. Even the long form here abbreviates the fact that the n on the right-hand side is silently treated as a real number using the standard embedding.
It is common to omit the parentheses around the argument when there is little chance of confusion, thus: sin x; this is known as prefix notation. Writing the function after its argument, as in x ƒ, is known as postfix notation; for example, the factorial function is customarily written n!, even though its generalization, the gamma function, is written Γ(n). Parentheses are still used to resolve ambiguities and denote precedence, though in some formal settings use of either prefix or postfix notation eliminates the need for any parentheses.
Functions with multiple inputs and outputs
The concept of function can be extended to an object that takes a combination of two (or more) argument values to a single result. This intuitive concept is formalized by a function whose domain is the Cartesian product of two or more sets.
For example, consider the multiplication function that associates two integers to their product: ƒ(x, y) = x·y. This function can be defined formally as having domain Z×Z , the set of all integer pairs; codomain Z; and, for graph, the set of all pairs ((x,y), x·y). Note that the first component of any such pair is itself a pair (of integers), while the second component is a single integer.
The function value of the pair (x,y) is ƒ((x,y)). However, it is customary to drop one set of parentheses and consider ƒ(x,y) a function of two variables (or with two arguments), x and y.
The concept can still further be extended by considering a function that also produces output that is expressed as several variables. For example consider the function swap(x, y) = (y, x) with domain R×R and codomain R×R as well. The pair (y, x) is a single value in the codomain seen as a cartesian product.
Currying
An alternative approach to handling functions with multiple arguments is to transform them into a chain of functions each of which takes a single argument. For instance one can interpret Add(3,5) as first produce a function that adds 3 to its argument, and then apply the 'Add 3' function to 5. This transformation is called currying, Add 3 is curry(Add) applied to 3. There is a bijection between the function spaces and . When working with curried functions it is customary to use prefix notation (with function application considered left-associative), since juxtaposition of multiple arguments—as in (ƒ x y)—naturally maps to evaluation of a curried function.
Binary operations
The familiar binary operations of arithmetic, addition and multiplication, can be viewed as functions from R×R to R. This view is generalized in abstract algebra, where n-ary functions are used to model the operations of arbitrary algebraic structures. For example, an abstract group is defined as a set X and a function ƒ from X×X to X that satisfies certain properties.
Traditionally, addition and multiplication are written in the infix notation: x+y and x×y instead of +(x, y) and ×(x, y).
Injective and surjective functions
Three important kinds of function are the injections (or one-to-one functions), which have the property that if ƒ(a) = ƒ(b) then a must equal b; the surjections (or onto functions), which have the property that for every y in the codomain there is an x in the domain such that ƒ(x) = y; and the bijections, which are both one-to-one and onto. This nomenclature was introduced by the Bourbaki group.
When the definition of a function by its graph only is used, since the codomain is not defined, the "surjection" must be accompanied with a statement about the set the function maps onto. For example, we might say ƒ maps onto the set of all real numbers.
Function composition

The function composition of two or more functions uses the output of one function as the input of another. The functions ƒ: X → Y and g: Y → Z can be composed by first applying ƒ to an argument x to obtain y = ƒ(x) and then applying g to y to obtain z = g(y). The composite function formed in this way from general ƒ and g may be written
This notation follows the form such that .
The function on the right acts first and the function on the left acts second, reversing English reading order. We remember the order by reading the notation as "g of ƒ". The order is important, because rarely do we get the same result both ways. For example, suppose ƒ(x) = x2 and g(x) = x+1. Then g(ƒ(x)) = x2+1, while ƒ(g(x)) = (x+1)2, which is x2+2x+1, a different function.
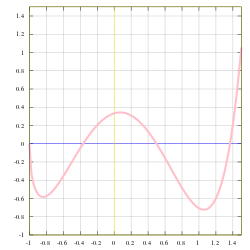
In a similar way, the function given above by the formula y = 5x−20x3+16x5 can be obtained by composing several functions, namely the addition, negation, and multiplication of real numbers.
An alternative to the colon notation, convenient when functions are being composed, writes the function name above the arrow. For example, if ƒ is followed by g, where g produces the complex number eix, we may write
A more elaborate form of this is the commutative diagram.
Identity function
The unique function over a set X that maps each element to itself is called the identity function for X, and typically denoted by idX. Each set has its own identity function, so the subscript cannot be omitted unless the set can be inferred from context. Under composition, an identity function is "neutral": if ƒ is any function from X to Y, then
Restrictions and extensions
Informally, a restriction of a function ƒ is the result of trimming its domain.
More precisely, if ƒ is a function from a X to Y, and S is any subset of X, the restriction of ƒ to S is the function ƒ|S from S to Y such that ƒ|S(s) = ƒ(s) for all s in S.
If g is any restriction of ƒ, we say that ƒ is an extension of g.
Inverse function
If ƒ is a function from X to Y then an inverse function for ƒ, denoted by ƒ−1, is a function in the opposite direction, from Y to X, with the property that a round trip (a composition) returns each element to itself. Not every function has an inverse; those that do are called invertible. The inverse function exists if and only if ƒ is a bijection.
As a simple example, if ƒ converts a temperature in degrees Celsius to degrees Fahrenheit, the function converting degrees Fahrenheit to degrees Celsius would be a suitable ƒ−1.
The notation for composition reminds us of multiplication; in fact, sometimes we denote it using juxtaposition, gƒ, without an intervening circle. Under this analogy, identity functions are like 1, and inverse functions are like reciprocals (hence the notation).
For functions which are injections or surjections, generalized inverse functions can be defined, called left and right inverses respectively. Left inverses map to the identity when composed to the left; right inverses when composed to the right.
Image of a set
The concept of the image can be extended from the image of a point to the image of a set. If A is any subset of the domain, then ƒ(A) is the subset of im ƒ consisting of all images of elements of A. We say the ƒ(A) is the image of A under f.
Use of ƒ(A) to denote the image of a subset A⊆X is consistent so long as no subset of the domain is also an element of the domain. In some fields (e.g. in set theory, where ordinals are also sets of ordinals) it is convenient or even necessary to distinguish the two concepts; the customary notation is ƒ[A] for the set { ƒ(x): x ∈ A }; some authors write ƒ`x instead of ƒ(x), and ƒ``A instead of ƒ[A].
Notice that the image of ƒ is the image ƒ(X) of its domain, and that the image of ƒ is a subset of its codomain.
Inverse image
The preimage (or inverse image, or more precisely, complete inverse image) of a subset B of the codomain Y under a function ƒ is the subset of the domain X defined by
So, for example, the preimage of {4, 9} under the squaring function is the set {−3,−2,2,3}.
In general, the preimage of a singleton set (a set with exactly one element) may contain any number of elements. For example, if ƒ(x) = 7, then the preimage of {5} is the empty set but the preimage of {7} is the entire domain. Thus the preimage of an element in the codomain is a subset of the domain. The usual convention about the preimage of an element is that ƒ−1(b) means ƒ−1({b}), i.e
In the same way as for the image, some authors use square brackets to avoid confusion between the inverse image and the inverse function. Thus they would write ƒ−1[B] and ƒ−1[b] for the preimage of a set and a singleton.
The preimage of a singeton set is sometimes called a fiber. The term kernel can refer to a number of related concepts.
Specifying a function
A function can be defined by any mathematical condition relating each argument to the corresponding output value. If the domain is finite, a function ƒ may be defined by simply tabulating all the arguments x and their corresponding function values ƒ(x). More commonly, a function is defined by a formula, or (more generally) an algorithm — a recipe that tells how to compute the value of ƒ(x) given any x in the domain.
There are many other ways of defining functions. Examples include piecewise definitions, induction or recursion, algebraic or analytic closure, limits, analytic continuation, infinite series, and as solutions to integral and differential equations. The lambda calculus provides a powerful and flexible syntax for defining and combining functions of several variables.
Computability
Functions that send integers to integers, or finite strings to finite strings, can sometimes be defined by an algorithm, which gives a precise description of a set of steps for computing the output of the function from its input. Functions definable by an algorithm are called computable functions. For example, the Euclidean algorithm gives a precise process to compute the greatest common divisor of two positive integers. Many of the functions studied in the context of number theory are computable.
Fundamental results of computability theory show that there are functions that can be precisely defined but are not computable. Moreover, in the sense of cardinality, almost all functions from the integers to integers are not computable. The number of computable functions from integers to integers is countable, because the number of possible algorithms is. The number of all functions from integers to integers is higher: the same as the cardinality of the real numbers. Thus most functions from integers to integers are not computable. Specific examples of uncomputable functions are known, including the busy beaver function and functions related to the halting problem and other undecidable problems.
Function spaces
The set of all functions from a set X to a set Y is denoted by X → Y, by [X → Y], or by YX.
The latter notation is motivated by the fact that, when X and Y are finite, of size |X| and |Y| respectively, then the number of functions X → Y is |YX| = |Y||X|. This is an example of the convention from enumerative combinatorics that provides notations for sets based on their cardinalities. Other examples are the multiplication sign X×Y used for the cartesian product where |X×Y| = |X|·|Y| , and the factorial sign X! used for the set of permutations where |X!| = |X|! , and the binomial coefficient sign used for the set of n-element subsets where
We may interpret ƒ: X → Y to mean ƒ ∈ [X → Y]; that is, "ƒ is a function from X to Y".
Pointwise operations
If ƒ: X → R and g: X → R are functions with common domain X and common codomain a ring R, then one can define the sum function ƒ + g: X → R and the product function ƒ ⋅ g: X → R as follows:
for all x in X.
This turns the set of all such functions into a ring. The binary operations in that ring have as domain ordered pairs of functions, and as codomain functions. This is an example of climbing up in abstraction, to functions of more complex types.
By taking some other algebraic structure A in the place of R, we can turn the set of all functions from X to A into an algebraic structure of the same type in an analogous way.
Other properties
There are many other special classes of functions that are important to particular branches of mathematics, or particular applications. Here is a partial list: Template:Multicol
- bijection, injection and surjection, or individually:
- continuous
- differentiable, integrable
History
Developments prior to 1850
The history of the function concept in mathematics is described by da Ponte (1992) [1]. The underlying idea of a function dates back to the Persian mathematician, Sharaf al-Dīn al-Tūsī, in the 12th century. In his analysis of the equation for example, he begins by changing the equation's form to . He then states that the question of whether the equation has a solution depends on whether or not the “function” on the left side reaches the value . To determine this, he finds a maximum value for the function. Sharaf al-Din then states that if this value is less than , there are no positive solutions; if it is equal to , then there is one solution; and if it is greater than , then there are two solutions.[2]
The notion of "function" in analysis
As a mathematical term, "function" was coined by Gottfried Leibniz, in a 1673 letter, to describe a quantity related to a curve, such as a curve's slope at a specific point.[3] [4] The functions Leibniz considered are today called differentiable functions. For this type of function, one can talk about limits and derivatives; both are measurements of the output or the change in the output as it depends on the input or the change in the input. Such functions are the basis of calculus.
Johann Bernoulli had, "by 1718, had come to regard a function as any expression made up of a variable and some constants" [5], and Leonhard Euler during the mid-18th century used the word to describe an expression or formula involving variables and constants e.g. x2 + 3*x + 2.[6]
Alexis Claude Clairaut (in approximately 1734) and Euler introduced the familiar notation " f(x) ".[7]
At first, the idea of a function was rather limited. Joseph Fourier, for example, claimed that every function had a Fourier series, something no mathematician would claim today. By broadening the definition of functions, mathematicians were able to study "strange" mathematical objects such as continuous functions that are nowhere differentiable. These functions were first thought to be only theoretical curiosities, and they were collectively called "monsters" as late as the turn of the 20th century. However, powerful techniques from functional analysis have shown that these functions are, in a precise sense, more common than differentiable functions. Such functions have since been applied to the modeling of physical phenomena such as Brownian motion.
During the 19th century, mathematicians started to formalize all the different branches of mathematics. Weierstrass advocated building calculus on arithmetic rather than on geometry, which favoured Euler's definition over Leibniz's (see arithmetization of analysis).
Dirichlet and Lobachevsky are traditionally credited with independently giving the modern "formal" definition of a function as a relation in which every first element has a unique second element. Eves asserts that "the student of mathematics usually meets the Dirichlet definition of function in his introductory course in calculus[8], but Dirichlet's claim to this formalization is disputed by Imre Lakatos:
- There is no such definition in Dirichlet's works at all. But there is ample evidence that he had no idea of this concept. In his [1837], for instance, when he discusses piecewise continuous functions, he says that at points of discontinuity the function has two values: ...
- (Proofs and Refutations, 151, Cambridge University Press 1976.)
In the context of "the Differential Calculus" George Boole defined (circa 1849) the notion of a function as follows:
- "That quantity whose variation is uniform . . . is called the independent variable. That quantity whose variation is referred to the variation of the former is said to be a function of it. The Differential calculus enables us in every case to pass from the function to the limit. This it does by a certain Operation. But in the very Idea of an Operation is . . . the idea of an inverse operation. To effect that inverse operation in the present instance is the business of the Int[egral] Calculus."[9].
The logician's "function"
Logicians of this time were primarily involved with analyzing syllogisms (the 2000 year-old Aristotelian forms and otherwise), or as Augustus De Morgan (1847) stated it: "the examination of that part of reafoning which depends upon the manner in which inferences are formed, and the inveftigation of general maxims and rules for conftructing arguments [sic: archaic]"[10]. At this time the notion of (logical) "function" is not explicit, but at least in the work of De Morgan and George Boole it is implied: we see abstraction of the argument forms, the introduction of variables, the introduction of a symbolic algebra, and some of the notions of set theory.
De Morgan's 1847 "FORMAL LOGIC OR, The Calculus of Inference, Neceffary [sic] and Probable" observes that "[a] logical truth depends upon the ftructure of the ftatement, and not upon the particular matters fpoken of"; he wastes no time (preface page i) abstracting: "In the form of the propofition, the copula is made as abfract as the terms". He immediately (p. 1) casts what he calls "the proposition" (present-day propositonal function) into a form such as "X is Y", where the symbols X, "is", and Y represent, respectively, the subject, copula, and predicate. While the word "function" does not appear, the abstraction is there, "variables" are there, the notion of inclusion in his symbolism “all of the Δ is in the О” (p. 9), and lastly a new symbolism for logical analysis, for example:
- " A1 X)Y To take an X it is necessary to take a Y" [or To be an X it is necessary to be a Y]
- " A1 Y)X To take an Y it is sufficient to take a X" [or To be a Y it is sufficient to be an X], etc.
In his 1848 The Nature of Logic Boole asserts that "logic . . . is in a more especial sense the science of reasoning by signs", and he briefly discusses the notions of "belonging to" and "class": "An individual may possess a great variety of attributes and thus belonging to a great variety of different classes" [11]. Like De Morgan he uses the notion of "varible" drawn from analysis; he gives an example of "represent[ing] the class oxen by x and that of horses by y and the conjunction and by the sign + . . . we might represent the aggregate class oxen and horses by x + y"
The logicist's "function": Development of the notion of "function" in logic 1850-1950
George Boole 1854; Venn 1881
In his An Investigation into the laws of thought Boole now defined a function in terms of a symbol x as follows:
- "8. Definition.-- Any algebraic expression involving symbol x is termed a function of x, and may be represented by the abbreviated form f(x)"[12]
As Boole used algebraic expressions to describe logical notions (e.g. 1−x is logical NOT(x), xy is the logical AND(x,y), etc), an algebraic function could represent a logical function as well.
By 1881 Venn in his Symbolic Logic was using the notions "function of propositions", "in extension", quantifying a variable, set inclusion etc. (Venn 1881:10). Indeed he equated unequivocally the notion of "logical function" with "class" [modern "set"]: "... on the view adopted in this book, f(x) never stands for anything but a logical class. It may be a compound class aggregated of many simple classes; it may be a class indicated by certain inverse logical operations [e.g. y=f-1(x)(Venn 1881:357)], it may be composed of two groups of classes equal to one another, or what is the same thing, their difference declared equal to zero, that is, a logical equation. But however composed or derived, f(x) with us will never be anything else than a general expression for such logical classes of things as may fairly find a place in ordinary Logic"[13].
Frege's Begriffsschrift 1879
Gottlob Frege (1879) preceded Guiseppe Peano (1889), but Peano had no knowledge of Frege 1879 until after he had published his 1889. Both works strongly influenced Bertrand Russell (1903). Russell in turn influenced much of twentieth-century mathematics through his Principia Mathematica (1913) jointly authored with Alfred North Whitehead.
Frege begins his discussion of "function" with an example: Begin with the expression[14] "Hydrogen is lighter than carbon dioxide". Now remove the sign for hydrogen (i.e. the word "hydrogen") and replace it with the sign for oxygen (i.e. the word "oxygen"); this makes a second statement. Do this again (using either statement) and substitute the sign for nitrogen (i.e. the word "nitrogen") and note that "This changes the meaning in such a way that "oxygen" or "nitrogen" enters into the relations in which "hydrogen" stood before"[15]. There are three statements:
- "Hydrogen is lighter than carbon dioxide."
- "Oxygen is lighter than carbon dioxide."
- "Nitrogen is lighter than carbon dioxide."
Now observe in all three a "stable component, representing the totality of [the] relations"[16]; call this the function, i.e.:
- "... is lighter than carbon dioxide", is the function.
Frege calls the argument of the function "[t]he sign [e.g. hydrogen, oxygen, or nitrogen], regarded as replaceable by others that denotes the object standing in these relations"[17]. He notes that we could have derived the function as "Hydrogen is lighter than . . .." as well, with an argument position on the right; the exact observation is made by Peano (see more below). Finally, Frege allows for the case of two (or more arguments). For example, remove "carbon dioxide" to yield the invariant part (the function) as:
- "... is lighter than ... "
The one-argument function Frege generalizes into the form Φ(A) where A is the argument and Φ( ) represents the function, whereas the two-argument function he symbolizes as Ψ(A, B) with A and B the arguments and Ψ( , ) the function and cautions that "in general Ψ(A, B) differs from Ψ(B, A)". Using his unique symbolism he translates for the reader the following symbolism:
- "We can read |--- Φ(A) as "A has the property Φ. |--- Ψ(A, B) can be translated by "B stands in the relation Ψ to A" or "B is a result of an application of the procedure Ψ to the object A"."[18]
Peano 1889 The Principles of Arithmetic
Peano became aware of Frege's work only after he had published his 1889[19]. Nevertheless he defined the notion of "function" in a manner somewhat similar to Frege, but without the precision[20]. First Peano defines s to be a class ("aggregate of objects")[21], the objects of which satisfy three simple equality-conditions: given "objects of the system s"[22], a = a, (a = b)=(b = a), IF ((a = b) AND (b = c)) THEN (a = c). He then introduces φ, "a sign or an aggregate of signs such that if x is an object of the class s, the expression φx denotes a new object". Peano adds two conditions on these new objects: First, that the three equality-conditions hold for the objects φx; secondly, that "if x and y are objects of class s and if x = y, we assume it is possible to deduce φx = φy"[23]. Given all these conditions are met, φ is a "function presign". Likewise he identifies a "function postsign". For example if φ is the function presign a+, then φx yields a+x, or if φ is the function postsign +a then xφ yields x+a[24].
Bertrand Russell 1903
The influence of Peano and Frege on Russell was profound. In his Appendix A "The Logical and Arithmetical Doctrines of Frege" Russell considers Frege's definition of function "very important, and [it] requires careful examination"[25]. As expressed by Russell "the process of transforming constants in a proposition into variables leads to what is called generalization, and gives us, as it were, the formal essence of a proposition ... So long as any term in our propostion can be turned into a variable, our proposition can be generalized; and so long as this is possible, it is the business of mathematics to do it"[26]; these generalizations Russell named propositional functions"[27]. Indeed he cites and quotes from Frege's Begriffsschrift (see previous section about Frege) and presents a vivid example from Frege's 1891 Function und Begriff: That "the essence of the arithmetical function 2*x3+x is what is left when the x is taken away, i.e. in the above instance 2*( )3 + ( ). The argument x does not belong to the function but the two taken together make the whole"[28].
For Russell the bedevilling notion is that of "variable": "6. Mathematical propositions are not only characterized by the fact that they assert implications, but also by the fact that they contain variables. The notion of the variable is one of the most difficult with which logic has to deal. For the present, I openly wish to make it plain that there are variables in all mathematical propositions, even where at first sight they might seem to be absent. . . . We shall find always, in all mathematical propositions, that the words any or some occur; and these words are the marks of a variable and a formal implication"[29].
He developed these definitions through his 1908 Mathematical logical as based on the theory of types and carried them into his and Whitehead's 1910-1913 Principia Mathematica.
Hardy 1908
Hardy 1908, pp. 26–28 defined a function as a relation between two variables x and y such that "to some values of x at any rate correspond values of y." He neither required the function to be defined for all values of x nor to associate each value of x to a single value of y. This broad definition of a function encompasses more relations than are ordinarily considered functions in contemporary mathematics.
The Formalist's "function": David Hilbert's axiomatization of mathematics (1904-1927), Kleene (1952)
David Hilbert's set himself the goal to "formalize" classical mathematics "as a formal axiomatic theory, and this theory shall be proved to be consistent, i.e. free from contradiction" [30]. In his 1927 The Foundations of Mathematics he frames the notion of function in terms of the existence of an "object":
- 13. A(a) --> A(ε(A)) Here ε(A) stands for an object of which the proposition A(a) certainly holds if it holds of any object at all; let us call ε the logical ε-function"[31].
Hilbert then illustrates the three ways how the ε-function is to be used, firstly as the "for all" and "there exists" notions, secondly to represent the "object of which [a proposition] holds", and lastly how to cast it into the choice function.
But the outcome of Hilbert's and his student Bernays's effort was unexpected; see Undecidability). In an effort to solve Hilbert's Entscheidungsproblem (1928), mathematicians set about to define what was meant by an "effective method" or "algorithm", that is, an explicit, step-by-step procedure that would succeed in computing a function. Various models for algorithms appeared, in rapid succession, including the lambda calculus, the μ-recursive functions and Turing machines. It was shown that all of these models could compute the same class of computable functions. Church's thesis holds that this class of functions exhausts all the number-theoretic functions that can be calculated by an algorithm.
Stephen Kleene in his 1952 Introduction to Metamathematics presented a definition of function that had evolved into a "correspondence" of elements, for example (he also offers a multi-valued version):
- "[A] (single-valued) function f or f(x) or y = f(x) of one variable x is a correspondence by which, to each element x of a set X there corresponds a single element y of a set Y"[32].
His usage of the words "independent variable", "domain", "range", "many-one", "argument", etc are in the now-conventional manner. He then goes further and notes that "what a many-one correspondence is to be, [is] according to the kind of theory one is working in. In set-theoretic terms, the correspondence can be identified with the set of all the ordered pairs (x,y) of corresponding elements of X and Y1. One may speak instead of the law or rule establishing the correspondence, at least in dealing with such functions that a law or rule in some understood sense can be given for each function. In the case that X is a finite set, a function can be given as a table[33].
Development of the set-theoretic definition
Set theory began with the work of the logicians with the notion of "class" (modern "set") for example de Morgan (1847), Jevons (1880), Venn 1881, Frege 1879 and Peano (1889). It was given a push by Georg Cantor's attempt to define the infinite (1870-1890) and a subsequent discovery of an antinomy (contradiction, paradox) in Cantor's treatment, by Russell's discovery (1902) of an antinomy in Frege's 1879, by the discovery of more antinomies in the early 1900's (e.g. the 1897 Burali-Forti paradox and the 1905 Richard paradox) and Russell's subsequent considerations of them, and by dislike of Russell's complex treatment of logic[34] and in particular his axiom of reducibility (1908, 1910-1913) that he proposed as a means to evade the antinomies.
Frege and Russell: Russell's paradox (1902)
In 1902 Russell sent a letter to Frege point out that Frege's 1879 Begriffsschrift allowed a function to be an argument of itself: "On the other hand, it may also be that the argument is determinate and the function indeterminate. In both cases [however] . . . the whole is decomposed into function and argument according to its content and not merely according to the point of view adopted"[35] From this loose situation Russell was able to form a paradox:
- "You state ... that a function, too, can act as the indeterminate element. This I formerly believed, but now this view seems doubtful to me because of the following contradiction. Let w be the predicate: to be a predicate that cannot be predicated of itself. Can w be predicated of itself?"[36]
Frege responded promptly that "... it has shaken the basis on which I intended to build arithmetic"[37].
From this point forward, for both the Logicists and the Formalists, development of the foundations of mathematics became an exercise in how to dodge "Russell's paradox", framed as it was in "the bare [set-theoretic] notions of set and element"[38]. van Heijenoort observed the subsequent split along the lines of Russell's "theory of types" and Zermelo's axiomatization of set theory; he observes that the "two responses are extremely different"[39]
Zermelo's set theory (1908)
The notion of "function" appears as axiom III -- the Axiom of separation (Axiom der Aussonderung). This axiom constrains one to "separate" a subset from a previously formed set. To do this one applies a "definite criterion" (property) to the pre-existing set via a " 'propositional function' F(x) in which the variable term x ranges over all individuals of a class K . . . [and the property] is definite for each single individual x of the class K[40]. But Zermelo's "definite criterion" is imprecise, and it will be fixed by Weyl, Fraenkel, Skolem and von Neumann into the contemporary form of e.g. Suppes 1960[41]
The notion of an "ordered pair"
The history of the notion of "ordered pair" is not clear. As noted above, Frege (1879) proposed an intuitive ordering in his definition of a two-argument function Ψ(A, B). Norbert Wiener in his 1914 (see below) observes that his own treatment essentially "revert(s) to Schröder's treatment of a relation as a class of ordered couples"[42]. Russell (1903) considered the definition of a relation (such as Ψ(A, B)) as a "class of couples" but rejected it:
- "There is a temptation to regard a relation as definable in extension as a class of couples. This is the formal advantage that it avoids the necessity for the primitive proposition asserting that every couple has a relation holding between no other pairs of terms. But it is necessary to give sense to the couple, to distingush the referent [domain] from the relatum [converse domain]: thus a couple becomes essentially distinct from a class of two terms, and must itself be introduced as a primitive idea. . . . It seems therefore more correct to take an intensional view of relations, and to identify them rather with class-concepts than with classes."[43]
By 1910-1913 and Principia Mathematica Russell had given up on the requirement for an intensional definition of a relation. But he ended up proposing his unpopular axiom of reducibility in its place. In response to the axiom of reducibility applied to relations Wiener would, in a few years, reduce a relation to a set of paired sets (i.e. ordered pair).
The Wiener-Hausdorff-Kuratowski definition of an ordered pair 1914-1921
An attempt to solve the problem of the antinomies led Russell to propose his "doctrine of types" in an appendix B of his 1903 The Principles of Mathematics[44]. In a few years he would refine this notion and propose in his 1908 The Theory of Types two axioms of reducibility, the purpose of which were to reduce impredicative antinomy-producing (single-variable) propositional functions and (dual-variable) relations into a predicative form; he and Alfred North Whitehead would carry this treatment over to their Principia Mathematica 1910-1913 with a further refinement called "a matrix"[45]. The first axiom is *12.1; the second is *12.11. To quote Wiener the second axiom *12.11 "is involved only in the theory of relations"[46]. Both axioms, however, were met with skepticism and resistance; see more at Axiom of reducibility. By 1914 Norbert Wiener, using Whitehead and Russell's symbolism, eliminated axiom *12.11 (the "two-variable" (relational) version of the axiom of reducibility) by expressing a relation as an ordered pair "using the null set. At appproximately the same time, Hausdorff (1914, p. 32) gave the definition of the ordered pair (a, b) as { {a,1}, {b, 2} }. A few years later Kuratowski (1921) offered a definition that has been widely useded ever since, namely { {a, b}, {a} }"[47]. As noted by Suppes (1960) "This definition . . . was historically important in reducing the theory of relations to the theory of sets[48].
von Neumann's set theory 1925
By 1925 Abraham Fraenkel (1922) and Thoralf Skolem (1922) had amended Zermelo's set theory of 1908. But von Neumann was not convinced that this axiomatization could not lead to the antinomies[49]. So he proposed his own theory, his 1925 An axiomatization of set theory. It explicitly contains a "contemporary", set-theoretic version of the notion of "function":
- "[Unlike Zermelo's set theory] [w]e prefer, however, to axiomatize not "set" but "function". The latter notion certainly includes the former. (More precisely, the two notions are completely equivalent, since a function can be regarded as a set of pairs, and a set as a function that can take two values.)"[50].
His axiomatization creates two "domains of objects" called "arguments" (I-objects) and "functions" (II-objects); where they overlap are the "argument functions" (I-II objects). He introduces two "universal two-variable operations" -- (i) the operation [x, y]: ". . . read 'the value of the function x for the argument y) and (ii) the operation (x, y): ". . . (read 'the ordered pair x, y'") whose variables x and y must both be arguments and which itself produces an argument (x,y)". To clarify the function pair he notes that "Instead of f(x) we write [f,x] to indicate that f, just like x, is to be regarded as a variable in this procedure". And to avoid the "antinomies of naive set theory, in Russell's first of all . . . we must forgo treating certain functions as arguments"[51]. He adopts a notion from Zermelo to restrict these "certain functions"[52]
Since 1950
The idea of structure-preserving functions, or homomorphisms, led to the abstract notion of morphism, the key concept of category theory. More recently, the concept of functor has been used as an analogue of a function in category theory.[53]
See also
References
Notes
- ^ Another short but useful history is found in Eves 1990 pages 234-235
- ^ Victor J. Katz, Bill Barton (October 2007), "Stages in the History of Algebra with Implications for Teaching", Educational Studies in Mathematics, 66 (2), Springer Netherlands: 185–201 [192], doi:10.1007/s10649-006-9023-7
- ^ Thompson, S.P; Gardner, M; Calculus Made Easy. 1998. Page 10-11. ISBN 0312185480.
- ^ Eves dates Leibniz's first use to the year 1694 and also similarly relates the usage to "as a term to denote any quantity connected with a curve, such as the coordinates of a point on the curve, the slope of the curve, and so on"(Eves 1990:234).
- ^ Eves 1990:234
- ^ Eves 1990:235
- ^ Eves 1990:235
- ^ Eves asserts that Dirichlet "arrived at the following formulation: "[The notion of] a variable is a symbol that represents any one of a set of numbers; if two variables x and y are so related that whenever a value is assigned to x there is automatically assigned, by some rule or correspondence, a value to y, then we say y is a (single-valued) function of x. The variable x . . . is called the independent variable and the variable y is called the dependent variable. The permissible values that x may assume constitute the domain of definition of the function, and the values taken on by y constitute the range of values of the function . . . it stresses the basic idea of a relationship between two sets of numbers" Eves 1990:235.
- ^ Boole circa 1849 Elementary Treatise on Logic not mathematical including philosophy of mathematical reasoning in Grattan-Guiness and Bornet 1997:40
- ^ De Morgan 1847:1
- ^ Boole 1848 in Grattan-Guiness and Bornet 1997:1, 2
- ^ Boole 1854:86
- ^ Venn 1881: 86-87
- ^ Frege's exact words are "expressed in our formula language" and "expression", cf Frege 1879 in van Heijenoort 1967:21-22.
- ^ This example is from Frege 1879 in van Heijenoort 1967:21-22
- ^ Frege 1879 in van Heijenoort 1967:21-22
- ^ Frege cautions that the function will have "argument places" where the argument should be placed as distinct from other places where the same sign might appear. For example, if the expression were "Hydrogen is lighter than the compound carbon plus two oxygen", with the substitution of "oxygen" for "hydrogen" in the position of the argument, a second expression would be "Oxygen is lighter than the compound carbon plus two oxygen". But he does not go deeper into how to signify these positions and Russell 1903 observes this.
- ^ Gottlob Frege (1879) in van Heijenoort 1967:21-24
- ^ For most of his logical symbolism and notions of propositions Frege credits "many writers, especially Boole". In footnote 1 he credits Boole 1847, 1848, 1854, Schröder 1877, Peirce 1880, Jevons 1883, MacColl 1877, 1878, 1878a, 1880 (Peano 1889 in van Heijenoort 1967:86).
- ^ "...Peano intends to conver much more ground than Frege does in his Begriffsschrif and his subsequent works, but he does not till that ground to any depth comparable to what Frege does in his self-alloted field" van Heijenoort 1967:85
- ^ Peano's exact words cf van Heijenoort 1967:89.
- ^ Peano's exact words cf van Heijenoort 1967:91.
- ^ All symbols used here are from VI. Functions in Peano 1889 in van Heijenoort 1967:91).
- ^ cf van Heijenoort 1967:93
- ^ Russell 1903:505
- ^ Russell 1903:7
- ^ Russell 1903:19
- ^ Russell 1903:505
- ^ Russell 1903:5-6
- ^ Kleene 1952:53
- ^ Hilbert in van Heijenoort 1967:466
- ^ Kleene 1952:32
- ^ Kleene 1952:34
- ^ cf Kleene 1952:45
- ^ Frege 1879 in van Heijenoort 1967:23
- ^ Russell (1902) Letter to Frege in van Heijenoort 1967:124
- ^ Frege (1902) Letter to Russell in van Heijenoort 1967:127
- ^ van Heijenoort's commentary to Russell's Letter to Frege in van Heijenoort 1967:124
- ^ cf van Heijenoort's commentary to Zermelo (1908) Investigations in the foundations of set theory I in van Heijenoort 1967:199. See also von Neumann's take on the split in his 1925 An axiomatization of set theory in van Heijenoort 1967:393; he throws the axiomatics of Formalists Hilbert and Bernays into the fray. Jourdain (1914) observed that a split occurred along Liebniz's calculus ratiocinator aspect of the logic of classes (via Boole, de Morgan, Jevons, Venn, C. S. Peirce, Schröder, Ladd-Franklin etc.) and the lingua characteristica aspect along the logicistic lines of Frege, Peano and Russell, cf the Preface by Philip Jourdain in Louis Couturat (1914) The Algebra of Logic, Open Court Publishing Company, Chicago and London.
- ^ Zermelo used antique German script rather than F and K; Zermelo 1908 in van Heijenoort 1967:201
- ^ cf van Heijenoort's commentary before Zermelo 1908 Investigations in the foundations of set theory I in van Heijenoort 1967:199
- ^ But Wiener offers no date or reference cf Wiener 1914 in van Heijenoort 1967:226
- ^ Russell 1903:99
- ^ Russell 1903:523-529
- ^ *12 The Hierarchy of Types and the axiom of Reducibility in Principia Mathematica 1913:161
- ^ Wiener 1914 in van Heijenoort 1967:224
- ^ commentary by van Heijenoort preceding Norbert Wiener's (1914) A simplification of the logic of relations in van Heijenoort 1967:224.
- ^ Suppes 1960:32. This same point appears in van Heijenoort's commentary before Wiener (1914) in van Heijenoort 1967:224.
- ^ von Neumann's critique of the history observes the split between the logicists (e.g. Russell et. al.) and the set-theorists (e.g. Zermelo et. al.) and the formalists (e.g. Hilbert), cf von Neumann 1925 in van Heijenoort 1967:394-396.
- ^ von Neumann 1925 in van Heijenoort 1967:396
- ^ All quotes from von Neumann 1925 in van Heijenoort 1967:397-398
- ^ This notion is not easy to summarize; see more at van Heijenoort 1967:397.
- ^ John C. Baez (1998). "Categorification".
{{cite journal}}: Cite journal requires|journal=(help); Unknown parameter|coauthors=ignored (|author=suggested) (help)
Sources
- Anton, Howard (1980), Calculus with Analytical Geometry, Wiley, ISBN 978-0-471-03248-9
- Bartle, Robert G. (1976), The Elements of Real Analysis (2nd ed.), Wiley, ISBN 978-0-471-05464-1
- Husch, Lawrence S. (2001), Visual Calculus, University of Tennessee, retrieved 2007-09-27
- Katz, Robert (1964), Axiomatic Analysis, D. C. Heath and Company.
- da Ponte, João Pedro (1992), "The history of the concept of function and some educational implications", The Mathematics Educator, 3 (2): 3–8, ISSN 1062-9017
- Thomas, George B.; Finney, Ross L. (1995), Calculus and Analytic Geometry (9th ed.), Addison-Wesley, ISBN 978-0-201-53174-9
- Youschkevitch, A. P. (1976), "The concept of function up to the middle of the 19th century", Archive for History of Exact Sciences, 16 (1): 37–85, doi:10.1007/BF00348305.
- Monna, A. F. (1972), "The concept of function in the 19th and 20th centuries, in particular with regard to the discussions between Baire, Borel and Lebesgue", Archive for History of Exact Sciences, 9 (1): 57–84, doi:10.1007/BF00348540.
- Kleiner, Israel (1989), "Evolution of the Function Concept: A Brief Survey", The College Mathematics Journal, 20 (4): 282–300, doi:10.2307/2686848.
- Ruthing, D. (1984), "Some definitions of the concept of function from Bernoulli, Joh. to Bourbaki, N.", Mathematical Intelligencer, 6 (4): 72–77.
- Dubinsky, Ed; Harel, Guershon (1992), The Concept of Function: Aspects of Epistemology and Pedagogy, Mathematical Association of America, ISBN 0883850818.
- Malik, M. A. (1980), "Historical and pedagogical aspects of the definition of function", International Journal of Mathematical Education in Science and Technology, 11 (4): 489–492, doi:10.1080/0020739800110404.
Sources for History section
- Boole, George (1854), An Investigation into the Laws of Thought on which are founded the Laws of Thought and Probabilies", Walton and Marberly, London UK; Macmillian and Company, Cambridge UK. Republished as a googlebook.
- Eves, Howard. (1990), Fundations and Fundamental Concepts of Mathematics: Third Edition, Dover Publications, Inc. Mineola, NY, ISBN 0-486-69609-X (pbk)
{{citation}}: Check|isbn=value: invalid character (help) - Frege, Gottlob. (1879), Begriffsschrift: eine der arithmetischen nachgebildete Formelsprache des reinen Denkens, Halle
- Grattan-Guinness, Ivor and Bornet, Gérard (1997), George Boole: Selected Manuscripts on Logic and its Philosophy, Springer-Verlag, Berlin, ISBN 3-7643-5456-9 (Berlin...)
{{citation}}: Check|isbn=value: invalid character (help)CS1 maint: multiple names: authors list (link) - Hardy, Godfrey Harold (1908), A Course of Pure Mathematics, Cambridge University Press (published 1993), ISBN 978-0-521-09227-2
- Russell, Bertrand (1903) The Principles of Mathematics: Vol. 1, Cambridge at the University Press, Cambridge, UK, republished as a googlebook.
- Suppes, Patrick (1960) Axiomatic Set Theory, Dover Publications, Inc, New York NY, ISBN 0-486-61630-4. cf his Chapter 1 Introduction.
- Venn, John (1881) Symbolic Logic, Macmillian and Co., London UK. Republished as a googlebook.
- van Heijenoort, Jean (1967, 3rd printing 1976), From Frege to Godel: A Source Book in Mathematical Logic, 1879-1931, Harvard University Press, Cambridge, MA, ISBN: 0-674-32449-8 (pbk)
- Gottlob Frege (1879) Begriffsschrift, a formula language, modeled upon that of arithmetic, for pure thought with commentary by van Heijenoort, pages 1-82
- Giuseppe Peano (1889) The principles of arithmetic, presented by a new method with commentary by van Heijenoort, pages 83-97
- Bertrand Russell (1902) Letter to Frege with commentary by van Heijenoort, pages 124-125. Wherein Russell announces his discovery of a "paradox" in Frege's work.
- Gottlob Frege (1902) Letter to Russell with commentary by van Heijenoort, pages 126-128.
- David Hilbert (1904) On the foundations of logic and arithmetic, with commentary by van Heijenoort, pages 129-138.
- Jules Richard (1905) The principles of mathematics and the problem of sets, with commentary by van Heijenoort, pages 142-144. The Richard paradox.
- Bertrand Russell (1908a) Mathematical logic as based on the theory of types, with commentary by Willard Quine, pages 150-182.
- Ernst Zermelo (1908) A new proof of the possibility of a well-ordering, with commentary by van Heijenoort, pages 183-198. Wherein Zermelo rales against Poincaré's (and therefore Russell's) notion of impredicative definition.
- Ernst Zermelo (1908a) Investigations in the foundations of set theory I, with commentary by van Heijenoort, pages 199-215. Wherein Zermelo attempts to solve Russell's paradox by structuring his axioms to restrict the universal domain B (from which objects and sets are pulled by definite properties) so that it itself cannot be a set, i.e. his axioms disallow a universal set.
- Norbert Wiener (1914) A simplification of the logic of relations, with commentary by van Heijenoort, pages 224-227
- John von Neumann (1925) An axiomatization of set theory, with commentary by van Heijenoort , pages 393-413. Wherein von Neumann creates "classes" as distinct from "sets" (the "classes" are Zermelo's "definite properties"), and now there is a universal set, etc.
- David Hilbert (1927) The foundations of mathematics by van Heijenoort, with commentary, pages 464-479.
- Whitehead, Alfred North and Russell, Bertrand (1913, 1962 edition), Principia Mathematica to *56, Cambridge at the University Press, London UK, no ISBN or US card catalog number.
External links
- The Wolfram Functions Site gives formulae and visualizations of many mathematical functions.
- Shodor: Function Flyer, interactive Java applet for graphing and exploring functions.
- xFunctions, a Java applet for exploring functions graphically.
- Draw Function Graphs, online drawing program for mathematical functions.
- Functions from cut-the-knot.
- Function at ProvenMath.
- Comprehensive web-based function graphing & evaluation tool

![{\displaystyle {\begin{aligned}&\scriptstyle f\colon [-1,1.5]\to [-1,1.5]\\&\textstyle x\mapsto {\frac {(4x^{3}-6x^{2}+1){\sqrt {x+1}}}{3-x}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/367545798d4c1d7748410deb9d03ea9faf400d6d)























