Parity of zero

Zero objects, divided into two equal groups

Zero is an even number. In other words, its parity—the quality of an integer being even or odd—is even. Zero fits the definition of "even number": it is an integer multiple of 2. As a result, zero exhibits the properties shared by all even numbers: 0 is divisible by 2, 0 is surrounded on both sides by odd integers, 0 is the sum of an integer with itself, and 0 objects can be split into two equal groups. Zero fits into the rules for sums and products of even numbers, such as even − even = even, so any alternate definition of "even number" would still need to include zero. Within the even numbers, zero plays a central role: it is the identity element of the group of even integers, and it is the starting case from which all other even natural numbers are recursively generated. Every integer divides 0, including each power of 2; in this sense, 0 is the most even number of all.

On the human level, the parity of 0 is less widely understood than the parity of 2 or 3. In reaction time experiments, most subjects are slower to identify 0 as even than other even numbers. Both students and teachers in primary education are prone to a misconception that the parity of zero is ambiguous, or simply that zero is odd. Several researchers in mathematics education have written that such misconceptions represent an opportunity for exploration. Reviewing sentences like 0 × 2 = 0 can expose students' apprehensions about calling 0 a number and using it in arithmetic. Discussing the parity of zero in class can spark vigorous debates as students encounter basic principles of mathematical reasoning, such as the importance of precise definitions. While understanding zero is a worthwhile goal in itself, evaluating the parity of this exceptional number is an early example of a pervasive theme in mathematics: the abstraction of a familiar concept to an unfamiliar and perhaps unexpected setting.

In education

A number is called even if it is an integer multiple of 2. Zero is an integer multiple of 2, namely 0 × 2, so zero is even.

Mathematically, no further proof is required, but more explanation is needed in the context of education. One issue concerns the foundations of the proof: the concise definition of "even" given above is not always appropriate. The subject of the parity of zero is often treated within the first two or three years of primary education, as the concept of even and odd numbers is introduced and developed. A student at this level may not yet have learned what "integer" or "multiple" means, much less how to multiply with 0. Additionally, stating a definition of parity for all integers can seem like an arbitrary conceptual shortcut if the only even numbers investigated so far are 2, 4, 6, 8, and higher. It can help to acknowledge that as the number concept is extended from positive integers to include zero and negative integers, so too number properties such as parity are extended in a nontrivial way.

Age-appropriate explanations that zero is even, then, return to the concrete interpretation of parity in terms of paired objects, or they emphasize the even-odd-alternation between numbers. Meanwhile a number of misconceptions about 0 must be combatted, such as the belief that 0 means nothing and has no properties.

Explanations

The box with 0 objects has no red object left over.

Early in elementary school, numbers are used to count the objects in a set. Parity may be introduced by making groups of two objects. If the objects in a set can be marked off into groups of two, with none left over, then the number of objects is even. Zero may be understood as the count of no objects; in more formal terms, it is the number of objects in the empty set. The empty set contains zero groups of two, and no object is left over from this grouping, so zero is even.

Although it is difficult to depict zero groups of two, or to draw attention to the nonexistence of a leftover object, this conception of the evenness of zero can be illustrated by comparing the empty set with other sets, as in the diagram on the right.

When the number line is introduced, if the even and odd numbers are distinguished visually, then their pattern becomes obvious:

The even and odd numbers alternate. Starting at any even number, counting up or down by twos reaches the other even numbers, and there is no reason to skip over zero.

Later, when students become familiar with more complex arithmetic expressions and operating on 0, evenness and oddness can be approached in terms of how numbers can be expressed. Every integer is either of the form (2 × ▢) + 0 or (2 × ▢) + 1; the former numbers are even and the latter are odd. For example, 1 is odd because 1 = (2 × 0) + 1, and 0 is even because 0 = (2 × 0) + 0. Making a table of these facts then reinforces the number line picture above.

Students' knowledge

% responses over time

The chart on the right depicts children's beliefs about the parity of zero, as they progress from Year 1 to Year 6. The data are from Len Frobisher, who conducted a pair of surveys of UK schoolchildren. Frobisher was interested in how knowledge of single-digit parity translates to knowledge of multiple-digit parity, and zero figures prominently in the results.

In a preliminary survey of nearly 400 seven-year-olds, 45% chose even over odd when asked the parity of zero. A follow-up investigation offered more choices: neither, both, and don't know. This time the number of children in the same age range identifying zero as even dropped to 32%. Success in deciding that zero is even initially shoots up and then levels off at around 50% in Years 3 to 6. For comparison, the easiest task, identifying the parity of a single digit, levels off at about 85% success.

In interviews, Frobisher elicited some of the students' reasoning. One fifth-year decided that 0 was even because it was found on the 2 times table. A couple fourth-years realized that zero can be split into equal parts: "no one gets owt if it's shared out." Another fourth-year reasoned "1 is odd and if I go down it's even." The interviews also revealed the misconceptions behind some incorrect responses. A second-year was "quite convinced" that zero was odd, on the basis that "it is the first number you count". A fourth-year referred to 0 as "none" and thought that it was neither odd nor even, since "it's not a number".

More in-depth investigations were conducted by Esther Levenson, Pessia Tsamir, and Dina Tirosh, who interviewed a pair of sixth-grade students who were performing highly in their mathematics class. One student preferred deductive explanations of mathematical claims, while the other preferred practical examples. Both students initially thought that 0 was neither even nor odd, for different reasons. Levenson et al.'s report in the Journal of Mathematical Behavior details the students' reasoning; one of the themes is that their beliefs about the parity of zero are consistent with their concepts of zero and division.

Group discussions

Often students will independently ask if zero is even; the Israel National Mathematics Curriculum reminds first grade teachers that zero is even, but advises that it is unnecessary to mention this unless the class brings it up. In one study, Annie Keith observed a class of 15 second grade students, who convinced each other that zero was an even number based on even-odd alternation and on the possibility of splitting a group of zero things in two equal groups.

Deborah Loewenberg Ball, a researcher specializing in mathematics instruction, has extensively analyzed an episode that occurred in her public school classroom of 22 third graders during the 1989–1990 school year. Ball asked the class for comments about even and odd numbers and zero, which they had just been discussing with a group of fourth-graders, and over the next six minutes the students made a variety of claims about the parity of zero, the rules for even numbers, and how mathematics is done. The claims about zero alone take many forms: Zero is not even or odd; Zero could be even; Zero is not odd; Zero has to be an even; Zero is not an even number; Zero is always going to be an even number; Zero is not always going to be an even number; Zero is even; Zero is special. Much of the discussion hinges around one student's comment that "even numbers make even numbers", but that zero is "special"; students seem to advance competing definitions of "even", all the while bringing up examples and counterexamples to each other's claims.

Ball later asked her students to reflect on this "particularly long and confusing discussion on even and odd numbers". One student commented that hearing other ideas had helped her understanding, and she now believed for the first time that zero was even. At the same time, another student had originally thought zero to be even but "got sort of mixed up" and wasn't sure whom to agree with. Ball finds it significant that the latter student expressed a desire to listen further to the discussion: in this sense, both students have learned something valuable about their own learning process. On another occasion, during a discussion on fractions, Ball asked the class whether voting is a good way to prove what is true in mathematics. One of the students returned to her experience of the discussion on zero, concluding that voting was ineffective in comparison to investigating patterns.

Teachers' knowledge

Researchers of mathematics education at the University of Michigan used the true-or-false prompt "0 is an even number", among many similar questions, in a 2000–2004 study of 700 primary teachers in the United States. For them the question exemplifies "common knowledge ... that any well-educated adult should have", and it is "ideologically neutral" in that the answer does not vary between traditional and reform mathematics. Overall performance in the study significantly predicted improvements in students' standardized test scores after taking the teachers' classes.

Many teachers harbor misconceptions about zero, although it is hard to quantify how many. The Michigan study did not publish data for individual questions. One report comes from Betty Lichtenberg, who wrote an article titled "Zero is an even number" in the journal The Arithmetic Teacher in 1972. Lichtenberg, an associate professor of mathematics education at the University of South Florida, draws on her experience with a course she and her colleagues taught on methods for teaching arithmetic. She reports that several sections of prospective elementary school teachers were given a true-or-false test including the item "Zero is an even number." They found it to be a "tricky question", and about two thirds answered "False".

The literature contains a couple data points concerning teachers' attitudes about students' attitudes. The National Council of Teachers of Mathematics's Principles and Standards for School Mathematics records a first grader's argument that zero is an even number: "If zero were odd, then 0 and 1 would be two odd numbers in a row. Even and odd numbers alternate. So 0 must be even..." In a survey of 10 college students preparing to teach mathematics, none of them thought that the argument sufficed as a mathematical proof. When they were told that it had been written by a first grader, most agreed that it was acceptable reasoning for that age level.

Numerical cognition

Scaling analysis of reaction times, showing separation of 0

Adults who do believe that zero is even can nevertheless feel unfamiliar or uncomfortable with the fact, enough to measurably slow them down in a reaction time experiment. For an experiment designed to investigate the task of parity determination, a numeral or a number word is flashed to the subject on a monitor, and a computer records the time it takes the subject to identify the number as odd or even by striking an appropriate button, such as a Morse key. Stanislas Dehaene, a pioneer in the field of numerical cognition, led a series of such experiments in the early 1990s. They showed that 0 was slower to process than other even numbers. Some variations of the experiment found delays as long as 60 milliseconds or about 10% of the average reaction time—a small difference but a significant one.

Dehaene's experiments were not designed specifically to investigate 0, but to compare competing models of how parity information is processed and extracted. The most specific extraction model, the mental calculation hypothesis, suggests that reactions to 0 should be fast: 0 is a small number, and it is easy to calculate 0 × 2 = 0. (Subjects are known to compute and name the result of multiplication by zero faster than multiplication of nonzero numbers, although they are slower to verify proposed results like 2 × 0 = 0.) The results of the experiments suggested that something quite different was happening: parity information was apparently being recalled from memory along with a cluster of related properties, such as being prime or a power of two. Both the sequence of powers of two and the sequence of positive evens 2, 4, 6, 8, ... are well-distinguished mental categories whose members are prototypically even. Zero belongs to neither list, hence the slower responses.

Repeated experiments have shown a delay at zero for subjects from a variety of national and linguistic backgrounds, representing both left to right and right to left writing systems; almost all right-handed; from 17–53 years of age; confronted with number names in numeral form, spelled out, and spelled in a mirror image. Dehaene's group did find one differentiating factor: mathematical expertise. In one of their experiments, students in the École Normale Supérieure were divided into two groups: those in literary studies and those studying mathematics, physics, or biology. The slowing at 0 was "essentially found in the [literary] group", and in fact, "before the experiment, some L subjects were unsure whether 0 was odd or even and had to be reminded of the mathematical definition".

This strong dependence on familiarity again undermines the mental calculation hypothesis. The effect also suggests that it is inappropriate to include zero in experiments where even and odd numbers are compared as a group. As one study puts it, "Most researchers seem to agree that zero is not a typical even number and should not be investigated as part of the mental number line."

History

It is difficult to say when in the history of mathematics the first person examined the parity of zero; there is no well-documented answer. What is certain is that even and odd numbers were known before the number zero was introduced. Indeed, this historical development parallels childrens' conceptual development. The algebraic properties of 0, such as the rule 0 × n = 0, were first systematically explored by Indian mathematicians such as Brahmagupta in the 7th century—relatively late in comparison to the early history of number theory.

Ancient Greek mathematicians generally considered 2 to be the first even number and 3 the first odd number, and some did not even recognize 2 as even. The number 1 was not a number at all, but a component of all other numbers; as such it had to be both even and odd, and therefore neither truly even nor truly odd. This dual role for 1 was a source of metaphysical discomfort; one historian asserts that the Greeks could have avoided the issue had they known about 0.

Motivating modern definitions

The precise definition of any mathematical term, such as "even" meaning "integer multiple of two", is ultimately a convention. Unlike "even", some mathematical terms are purposefully constructed to exclude especially trivial or degenerate cases. Prime numbers are a famous example. The definition of "prime number" has historically shifted from "positive integer with at most 2 factors" to "positive integer with exactly 2 factors", with the effect that 1 is no longer considered prime. Most authors rationalize this shift by observing that the modern definition more naturally suits mathematical theorems that concern the primes. For example, the fundamental theorem of arithmetic is easier to state when 1 is not considered prime.

It would be possible to similarly redefine the term "even" in a way that no longer includes zero. However, in this case, the new definition would make it more difficult to state theorems concerning the even numbers. Already the effect can be seen in the the algebraic rules governing even and odd numbers. The most relevant rules concern addition, subtraction, and multiplication:

• even ± even = even
• odd ± odd = even
• even × integer = even

Inserting appropriate values into the left sides of these rules, one can produce 0 on the right sides:

• 2 − 2 = 0
• −3 + 3 = 0
• 4 × 0 = 0

The above rules would therefore be incorrect if zero were not even; at best they would have to be modified in some way. For example, one test study guide asserts that even numbers are characterized as integer multiples of two, but zero is "neither even nor odd". Accordingly, the guide's rules for even and odd numbers contain some exceptions:

• even ± even = even (or zero)
• odd ± odd = even (or zero)
• even × nonzero integer = even

Making an exception for zero in the definition of evenness forces one to make such exceptions in the rules for even numbers. From another perspective, taking the rules obeyed by positive even numbers, and requiring that they continue to hold for all integers, forces the usual definition and the evenness of zero.

Countless results in number theory invoke the fundamental theorem of arithmetic and the algebraic properties of even numbers, so the above choices have far-reaching consequences. For example, the fact that numbers have unique factorizations means that one can determine whether a number has an even or odd number of distinct prime factors. Since 1 is not prime, nor does it have any other prime factors, it is a product of 0 distinct primes; since 0 is an even number, 1 has an even number of distinct prime factors. This implies that the Möbius function takes the value μ(1) = 1, which is necessary for it to be a multiplicative function and for the Möbius inversion formula to work, and affects the exact value of the Mertens function everywhere. Some other mathematical contexts, where the presence of 0 in the even numbers can be felt, follow.

Mathematical contexts

Most of the intuitive reasons why zero is even fall under a few themes:

• Zero is not odd.
• Zero must be even to preserve the alternation between even and odd numbers.
• Zero must be even to preserve algebraic relations among even numbers.
• Zero is even because the empty set can be split into corresponding halves.
• Zero is even because it is divisible by 2.

These themes then reappear in many broader, more abstract mathematical structures. Even and odd numbers have countless applications and generalizations in mathematics, in which the evenness of zero often has identifiable consequences and analogies. Some of these follow.

Not being odd

The observation that zero is not odd is sometimes directly applied in a mathematical argument. If an unknown number is proven to be odd, then it cannot be zero. This apparently trivial observation occasionally provides a convenient and revealing proof that a number is nonzero. In the following examples, a problem lends itself to determining that a number of interest is odd, and an investigation of its parity helps identify the underlying mechanism that forces the number to be nonzero.

A classic result of graph theory states that a graph of odd order always has at least one even vertex. (Already this statement requires zero to be even and not odd in two places: the empty graph cannot have odd order, and an isolated vertex must be even.) In order to prove the statement, it is actually easier to prove a stronger result: any odd-order graph has an odd number of even vertices. The appearance of this odd number is explained by a still more general result, known as the handshaking lemma: any graph has an even number of vertices of odd degree. Finally, the even number of odd vertices is naturally explained by the degree sum formula.

Sperner's lemma is a more advanced application of the same strategy. Rather than prove that there exists at least one completely labeled subsimplex by directly constructing it, it is more convenient to prove that there exist an odd number of such subsimplices through an induction argument. A still stronger statement of the lemma then explains why this number is odd: it naturally breaks down as (n + 1) + n when one segregates colorings by orientation.

Even-odd alternation

Recursive definition of natural number parity

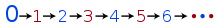
Zero is the starting point of the even natural numbers. The fact that zero is even, together with the fact that even and odd numbers alternate, is enough to determine the parity of every other natural number. This property can be formalized into a recursive definition of the set of even natural numbers:

• 0 is even.
• (n + 1) is even if and only if n is not even.

This definition has the conceptual advantage of relying only on the minimal foundations of the natural numbers: the existence of 0 and of successors. As such, it is useful for computer logic systems such as the Isabelle theorem prover. With this definition, the evenness of zero is not a theorem but an axiom. Indeed, "zero is an even number" may be interpreted as one of the Peano axioms, of which the even natural numbers are a model. A similar construction extends the definition of parity to transfinite ordinal numbers: every limit ordinal is even, including zero, and successors of even ordinals are odd.

Point in polygon test

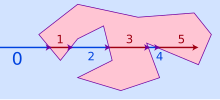
The classic point in polygon test from computational geometry applies the above ideas. To determine if a point lies within a polygon, one casts a ray from infinity to the point and counts the number of times the ray crosses the edge of polygon. The crossing number is even if and only if the point is outside the polygon. This algorithm works because if the ray never crosses the polygon, then its crossing number is zero, which is even, and the point is outside. Every time the ray does cross the polygon, the crossing number switches between even and odd, and the point at its tip switches between inside and outside.

Constructing a bipartition

Another application comes from the field of graph theory. A graph whose vertices are split into two groups, such that two vertices from the same group are never adjacent, is called a bipartite graph. If a (connected) graph has no odd cycles, then an explicit bipartition can be constructed by choosing a base vertex v and coloring every vertex black or white, depending on whether its distance from v is even or odd. Since the distance between v and itself is 0, and 0 is even, the base vertex is colored the opposite color as its neighbors, which lie at a distance of 1.

Algebra

2Z (blue) as subgroup of Z

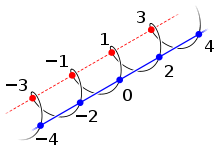
The evenness of zero appears in the structured context of abstract algebra. The fact that the additive identity (zero) is even, together with the evenness of sums and additive inverses of even numbers and the associativity of addition, means that the even integers form a group. Moreover, the group of even integers under addition is a subgroup of the group of all integers; this is an elementary example of the subgroup concept. The earlier observation that the rule "even − even = even" forces 0 to be even is part of a general pattern: any nonempty subset of an additive group that is closed under subtraction must be a subgroup, and in particular, must contain the identity.

Since the even integers form a subgroup of the integers, they partition the integers into cosets. These cosets may be described as the equivalence classes of the following equivalence relation: x ~ y if (x − y) is even. Here, the evenness of zero is directly manifested as the reflexivity of the binary relation ~. There are only two cosets of this subgroup—the even and odd numbers—and it can be used as a template for subgroups with index 2 in other groups as well. A well-known example is the alternating group as a subgroup of the symmetric group on n letters. The elements of the alternating group, called even permutations, can be completely characterized as products of even numbers of transpositions. The identity map, an empty product of no transpositions, is an even permutation since zero is even; it is the identity element of the group.

Adding in the rule "even × integer = even" means that the even numbers form an ideal in the ring of integers, and the above equivalence relation can be described as equivalence modulo this ideal. In particular, even integers are exactly those integers k where k ≡ 0 (mod 2). This formulation is useful for investigating integer zeroes of polynomials.

The empty set

A mirror partitions an empty collection of pencils; half (0) are real and half (0) are reflections.

One way of interpreting the evenness of zero is to say that a set with 0 elements can be partitioned into two subsets of equal size. The cardinality concept of size requires that there exists a bijection between these two subsets. In general, a set A has even cardinality if a partition of A into disjoint sets B and C exists where |B| = |C|, and thus |A| = 2|B| = 2|C|. The empty set can be partitioned trivially as Ø = Ø ∪ Ø, which immediately shows that 0 = |Ø| is even. This can also show that 0 is divisible by any integer n, since Ø = Ø ∪ Ø ∪ · · · ∪ Ø (n copies).

The essentials of the above structure can be specified in more compact language: a finite set has even cardinality iff it supports an involution without fixed points or, equivalently, a free action by Z/2. The empty set, having zero elements, does support such an involution, namely the empty function. Fixed-point-free involutions are mostly studied not on finite sets but on topological spaces, where the most important examples are the antipodal maps on n-dimensional spheres Sⁿ. The involution on the empty set is a base example: it is the antipodal map on S ⁻¹, the sphere of dimension negative one. In general, for a closed manifold to support a free involution, it must have an even Euler characteristic. The Euler characteristic of the empty set S ⁻¹ is the same as the Euler characteristic of any other odd-dimensional sphere, and it is an even number: zero.

Degrees of evenness

Some multiples of 2 are more even than others. The ancient Greeks already categorized the even numbers as singly and doubly even; 0 is doubly even because it is a multiple of 4, so it can be divided by 2 twice. More generally, 0 is divisible by any number, including any power of two, and this unique property of 0 has some interesting consequences.

One consequence appears in computer algorithms such as the Cooley–Tukey FFT, in which numbers appear in bit-reversed order. This ordering has the property that the farther to the left the first 1 occurs in a number's binary expansion, or the more times it is divisible by 2, the sooner it appears. Zero's bit reversal is still zero; it can be divided by 2 any number of times, and its binary expansion does not contain any 1s, so it always comes first. The illustration on the right depicts the evenness of the integers from +64 to −64.

The 2-adic integers (black points). Arrows point to 0 and powers of 2.

It is clear that 0 is divisible by 2 more times than any other number, but one runs into trouble when trying to quantify exactly how many times that is. For any nonzero integer (or rational number) n, one may define the 2-adic order of n, an integer which can be described as the number of times n is divisible by 2, or the exponent of the largest power of 2 that divides n, or the multiplicity of 2 in the prime factorization of n. But none of these descriptions works for 0; no matter how many times 0 is halved, it can still be halved again. Rather, the usual convention is to set the 2-order of 0 to be infinity as a special case. This convention is not peculiar to the 2-order; it is one of the axioms of an additive valuation in higher algebra.

The powers of two—1, 2, 4, 8, ...—form a simple sequence of increasingly even numbers. There are mathematically interesting ways to force such sequences to actually converge to zero, including the construction of the 2-adic numbers.

Everyday contexts

Some of the contexts where the parity of zero makes an appearance are purely rhetorical:

• It provides material for Internet message boards and ask-the-expert websites.
• Linguist Joseph Grimes muses that asking "Is zero an even number?" to married couples is a good way to get them to disagree.
• Social theorist Anthony Wilden proposes that all rules have exceptions, giving an example: "Whole numbers are either odd or even, but zero is neither one nor the other."
• Columnist Tony Snow once wrote, "Question: Name one thing beneath Bill Clinton's dignity. Answer: This is a trick question, like asking whether zero is odd or even. It has no known answer." The attack on Clinton was to be expected; a few readers who protested the comparison were more concerned with the mathematical error.
• Around the turn of the third millennium, several media outlets noted a pair of unusual milestones: "11/19/1999" was the last date composed of all odd digits that would occur for a very long time, and that "02/02/2000" was the first all-even date to occur in a very long time. Since these results make use of 0 being even, some readers were not entirely on board with the idea.

There are also some situations where calling zero even or not has consequences:

One third-party study guide for the GMAT states that 0 is not even, but the test's authors publish an official study guide that explicitly includes 0 in the even numbers. The correct answers to some of the GMAT's "data sufficiency" questions require that the usual rules for even numbers, such as n being even if (n + 2) is even, hold without exception for 0. Even on other standardized tests, if a question asks about the behavior of even numbers, it might be necessary to keep in mind that zero is even.

The nominal evenness of zero is relevant to odd-even rationing systems. Cars might be allowed to drive or to purchase gasoline on alternate days, according to the parity of the last digit in their license plates. Half of the numbers in a given range end in 0, 2, 4, 6, 8 and the other half in 1, 3, 5, 7, 9, so it makes sense to include 0 with the other even numbers. The relevant legislation sometimes stipulates that zero is even to avoid confusion. In fact, an odd-even restriction on driving in 1977 Paris did lead to confusion when the rules were unclear. On an odd-only day, the police avoided fining drivers whose plates ended in 0, because they did not know whether 0 was even.

In other situations, it can make sense to separate 0 from the other even numbers. On U.S. Navy vessels, even-numbered compartments are found on the port side, but zero is reserved for compartments that intersect the centerline. That is, the numbers read ...6420135... from port to starboard.

In the game of roulette, the casino has an interest in making sure that less than half of the numbers are counted as even. Thus the number 0 does not count as even or odd; a bet placed on either even or odd does not win if the ball falls on "0" or "00". The exact result depends on local rules, but the overall effect is to give the house an edge on "even money" bets. Similarly, the parity of zero can affect payoffs in prop bets when the outcome depends on whether some randomized number is odd or even, and it turns out to be zero. Bookmaker Stan James offers a "cricket roulette" in which a batsman who is dismissed for a duck wins for the bank.

The game odds and evens is also affected: if both players cast zero fingers, who wins? The strategy of the game varies with the agreed-upon answer; generally zero is counted as even. In fact, playing this game has been suggested as a way of introducing children to the concept that 0 is divisible by 2.

References

• Ball, Deborah Loewenberg (2003). "Using Content Knowledge in Teaching: What Do Teachers Have to Do, and Therefore Have to Learn?". Archive of the Third Annual Conference on Sustainability of Systemic Reform. Retrieved 2007-10-01. {{cite conference}}: Unknown parameter |booktitle= ignored (|book-title= suggested) (help)

  This talk includes a discussion on age-appropriate definitions for students. Ball has also written several articles on her classroom experience with students debating the evenness of zero; see the footnotes, further reading, and her website for more.

• Dehaene, Stanislas, Serge Bossini, and Pascal Giraux (1993). "The mental representation of parity and numerical magnitude" (PDF). Journal of Experimental Psychology: General. 122 (3): 371–396. doi:10.1037/0096-3445.122.3.371. Retrieved 2007-09-13.{{cite journal}}: CS1 maint: multiple names: authors list (link)

  This research report includes an overview of hypotheses in the field as well as a variety of experiments, with analysis of the SNARC effect and slowdowns at the numbers 0 and 6.

• Frobisher, Len (1999). "Primary School Children's Knowledge of Odd and Even Numbers". In Anthony Orton (ed.) (ed.). Pattern in the Teaching and Learning of Mathematics. London: Cassell. pp. 31–48. {{cite conference}}: |editor= has generic name (help); Unknown parameter |booktitle= ignored (|book-title= suggested) (help)

  An overview of history and teaching practices, with survey data; zero is treated on pages 40–41.

• Levenson, Esther, Pessia Tsamir, and Dina Tirosh (2007). "Neither even nor odd: Sixth grade students' dilemmas regarding the parity of zero". The Journal of Mathematical Behavior. 26 (2): 83–95. doi:10.1016/j.jmathb.2007.05.004.{{cite journal}}: CS1 maint: multiple names: authors list (link)

  This report starts with another solid overview of the problem, then focuses on two particular students in much greater depth than other articles. "In this study we investigate the extension of the natural numbers to include zero and the use of [mathematically based] and [practically based] explanations when integrating parity, the property of being even or odd, into this extended system."

• Lichtenberg, Betty Plunkett (1972). "Zero is an even number". The Arithmetic Teacher. 19 (7): 535–538. {{cite journal}}: Unknown parameter |month= ignored (help)

  This article covers a variety of age-appropriate explanations for why zero is even, with illustrations.

• Nuerk, Hans-Christoph, Wiebke Iversen, and Klaus Willmes (2004). "Notational modulation of the SNARC and the MARC (linguistic markedness of response codes) effect". The Quarterly Journal of Experimental Psychology A. 57 (5): 835–863. doi:10.1080/02724980343000512. {{cite journal}}: Unknown parameter |month= ignored (help)CS1 maint: multiple names: authors list (link)

  This more-recent survey of numerical cognition research touches at several points on the implications of zero's special status for the design and interpretation of experiments.

Further reading

• Ball, Deborah Loewenberg (1989). "Breaking with experience in learning to teach mathematics: the role of a preservice methods course". East Lansing, MI: National Center for Research on Teacher Education. {{cite journal}}: Cite journal requires |journal= (help)
• Ball, Deborah Loewenberg (1997). "What do students know? Facing challenges of distance, context, and desire in trying to hear children". In B. Biddle, T. Good, & I. Goodson (ed.). International handbook on teachers and teaching (PDF). Vol. 2. Dordrecht, Netherlands: Kluwer Press. pp. 679–718. Retrieved 23 August 2009.{{cite book}}: CS1 maint: multiple names: editors list (link)
• Ball, Deborah Loewenberg; Bass, Hyman (2000). "Interweaving content and pedagogy in teaching and learning to teach: Knowing and using mathematics". In J. Boaler (ed.). Multiple perspectives on the teaching and learning of mathematics (PDF). Westport, CT: Ablex. pp. 83–104. Retrieved 23 August 2009.
• Ball, Deborah Loewenberg; Bass, Hyman (2000). "Making believe: The collective construction of public mathematical knowledge in the elementary classroom". In D. Phillips (ed.). Yearbook of the National Society for the Study of Education, Constructivism in Education (PDF). Chicago: University of Chicago Press. pp. 193–224. Retrieved 23 August 2009.
• Barnett, S. (1990). Matrices: methods and applications. Oxford Applied Mathematics and Computing Science Series. p. 115.
• Cameron, Peter Jephson (1994). Combinatorics: topics, techniques, algorithms. p. 167.
• Dulski, Thomas R. (1999). Trace elemental analysis of metals: methods and techniques. p. 549.
• Evans, James Robert; Minieka, Edward (1992). Optimization algorithms for networks and graphs (2nd ed.). p. 283.
• Fias, Wim (2001). "Two routes for the processing of verbal numbers: evidence from the SNARC effect". Psychological Research. 65 (4): 250–259. doi:10.1007/s004260100065. PMID 11789429. {{cite journal}}: Unknown parameter |month= ignored (help)
• Golomb, Solomon Wolf (1994). Polyominoes: Puzzles, Patterns, Problems, and Packings. Princeton: Princeton University Press. p. 119. ISBN 0-691-02444-8.
• Kalsi, P S (2004). Spectroscopy of Organic Compounds (6th ed.). New Age International Publishers. p. 437.
• Koshy, Thomas (2004). Discrete mathematics with applications. Elsevier. p. 765.
• Leinhardt, Gaea; Steele, Michael D. (2005). "Seeing the Complexity of Standing to the Side: Instructional Dialogues". Cognition and Instruction. 23 (1). Lawrence Erlbaum: 87–163. doi:10.1207/s1532690xci2301_4. ERIC # EJ724916.
• Lengyel, Tamas (1994). "Characterizing the 2-adic order of the logarithm" (PDF). The Fibonacci Quarterly. 32: 397–401. Retrieved 23 August 2009.
• Merttens, Ruth; Vass, Jeff (1990). Sharing maths cultures: IMPACT, Inventing Maths for Parents and Children and Teachers. The Falmer Press. p. 70.
• Peterson, Penelope L. (1994). "Research Studies as Texts: Sites for Exploring the Beliefs and Learning of Researchers and Teachers". In Ruth Garner and Patricia A. Alexander (ed.). Beliefs about Text and Instruction with Text (1st ed.). pp. 93–120.
• Schoenfeld, Alan H. (2002). J. Brophy (ed.). "Social constructivist teaching: Its affordances and constraints" (PDF). Advances in Research on Teaching. 9. Elsevier. doi:10.1016/S1479-3687(02)80007-4. ISBN 0-7623-0873-7. Retrieved 23 August 2009. {{cite journal}}: |chapter= ignored (help); Cite journal requires |journal= (help)
• Stirling, David S. G. (1997). Mathematical analysis and proof. Albion Mathematics & Applications Series (1st ed.). p. 225.
• United States Senate Committee on Energy and Natural Resources, Subcommittee on Energy Conservation and Supply (1980). Energy Management Partnership Act of 1979: hearing before the Subcommittee on Energy Conservation and Supply of the Committee on Energy and Natural Resources, United States Senate, Ninety-sixth Congress, first session on S. 1280. Washington, D.C.: U.S. G.P.O. LCCN 80602009.