Doppler effect: Difference between revisions

Content deleted Content added

Inline

Revision as of 04:09, 26 February 2014

An animation illustrating how the Doppler effect causes a car engine or siren to sound higher in pitch when it is approaching than when it is receding. The pink circles are sound waves. When the car is moving to the left, each successive wave is emitted from a position further to the left than the previous wave. So for an observer in front (left) of the car, each wave takes slightly less time to reach him than the previous wave. The waves "bunch together", so the time between arrival of successive wavefronts is reduced, giving them a higher frequency. The waves "stretch apart", so the time between the arrival of successive wave-fronts is increased slightly, giving them a lower frequency.

The Doppler effect (or Doppler shift), named after the Austrian physicist Christian Doppler, who proposed it in 1842 in Prague, is the change in frequency of a wave (or other periodic event) for an observer moving relative to its source. It is commonly heard when a vehicle sounding a siren or horn approaches, passes, and recedes from an observer. Compared to the emitted frequency, the received frequency is higher during the approach, identical at the instant of passing by, and lower during the recession.

The relative changes in frequency can be best explained as follows. When the source of the waves is moving toward the observer, each successive wave crest is emitted from a position closer to the observer than the previous wave. Therefore each wave takes slightly less time to reach the observer than the previous wave. Therefore the time between the arrival of successive wave crests at the observer is reduced, causing an increase in the frequency. While they are travelling, the distance between successive wave fronts is reduced; so the waves "bunch together". Conversely, if the source of waves is moving away from the observer, each wave is emitted from a position farther from the observer than the previous wave, so the arrival time between successive waves is increased, reducing the frequency. The distance between successive wave fronts is increased, so the waves "spread out".

For waves that propagate in a medium, such as sound waves, the velocity of the observer and of the source are relative to the medium in which the waves are transmitted. The total Doppler effect may therefore result from motion of the source, motion of the observer, or motion of the medium. Each of these effects is analyzed separately. For waves which do not require a medium, such as light or gravity in general relativity, only the relative difference in velocity between the observer and the source needs to be considered.

Development

Doppler first proposed the effect in 1842 in his treatise "Über das farbige Licht der Doppelsterne und einiger anderer Gestirne des Himmels" (On the coloured light of the binary stars and some other stars of the heavens).^[1] The hypothesis was tested for sound waves by Buys Ballot in 1845.^[2] He confirmed that the sound's pitch was higher than the emitted frequency when the sound source approached him, and lower than the emitted frequency when the sound source receded from him. Hippolyte Fizeau discovered independently the same phenomenon on electromagnetic waves in 1848 (in France, the effect is sometimes called "effet Doppler-Fizeau" but that name was not adopted by the rest of the world as Fizeau's discovery was six years after Doppler's proposal).^[3] In Britain, John Scott Russell made an experimental study of the Doppler effect (1848).^[4]

General

Stationary sound source produces sound waves at a constant frequency $f$ , and the wave-fronts propagate symmetrically away from the source at a constant speed c. The distance between wave-fronts is the wavelength. All observers will hear the same frequency, which will be equal to the actual frequency of the source where $f = f 0$ .

The same sound source is radiating sound waves at a constant frequency in the same medium. However, now the sound source is moving with a speed $υ s = 0.7 c$ (Mach 0.7). Since the source is moving, the centre of each new wavefront is now slightly displaced to the right. As a result, the wave-fronts begin to bunch up on the right side (in front of) and spread further apart on the left side (behind) of the source. An observer in front of the source will hear a higher frequency $f = .mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}⁠c + 0/c - 0.7c⁠ f0 = 3.33 f0$ and an observer behind the source will hear a lower frequency $f = ⁠ c - 0 / c + 0.7 c ⁠ f 0 = 0.59 f 0$ .

Now the source is moving at the speed of sound in the medium ( $υ s = c$ , or Mach 1). The wave fronts in front of the source are now all bunched up at the same point. As a result, an observer in front of the source will detect nothing until the source arrives where $f = ⁠ c + 0 / c - c ⁠ f 0 = \infty$ and an observer behind the source will hear a lower frequency $f = ⁠ c - 0 / c + c ⁠ f 0 = 0.5 f 0$ .

The sound source has now broken through the sound speed barrier, and is traveling at 1.4 c (Mach 1.4). Since the source is moving faster than the sound waves it creates, it actually leads the advancing wavefront. The sound source will pass by a stationary observer before the observer hears the sound. As a result, an observer in front of the source will detect $f = ⁠ c + 0 / c - 1.4 c ⁠ f 0 = -2.5 f 0$ and an observer behind the source will hear a lower frequency $f = ⁠ c - 0 / c + 1.4 c ⁠ f 0 = 0.42 f 0$ .

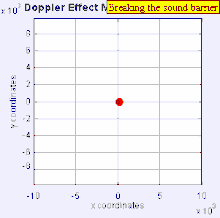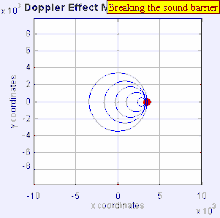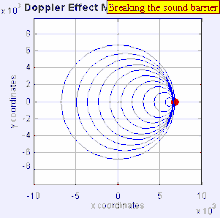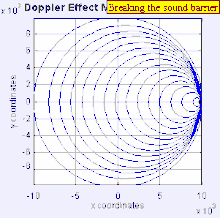
In classical physics, where the speeds of source and the receiver relative to the medium are lower than the velocity of waves in the medium, the relationship between observed frequency $f$ and emitted frequency $f_{\text{0}}$ is given by:^[5]

f=\left({\frac {c+v_{\text{r}}}{c+v_{\text{s}}}}\right)f_{0}\,

where

c\;

is the velocity of waves in the medium;

v_{\text{r}}\,

is the velocity of the receiver relative to the medium; positive if the receiver is moving towards the source (and negative in the other direction);

v_{\text{s}}\,

is the velocity of the source relative to the medium; positive if the source is moving away from the receiver (and negative in the other direction).

The frequency is decreased if either is moving away from the other.

The above formula assumes that the source is either directly approaching or receding from the observer. If the source approaches the observer at an angle (but still with a constant velocity), the observed frequency that is first heard is higher than the object's emitted frequency. Thereafter, there is a monotonic decrease in the observed frequency as it gets closer to the observer, through equality when it is coming from a direction perpendicular to the relative motion (and was emitted at the point of closest approach; but when the wave is received, the source and observer will no longer be at their closest), and a continued monotonic decrease as it recedes from the observer. When the observer is very close to the path of the object, the transition from high to low frequency is very abrupt. When the observer is far from the path of the object, the transition from high to low frequency is gradual.

If the speeds $v_{\text{s}}\,$ and $v_{\text{r}}\,$ are small compared to the speed of the wave, the relationship between observed frequency $f$ and emitted frequency $f_{\text{0}}$ is approximately^[5]

Observed frequency	Change in frequency
$f=\left(1+{\frac {\Delta v}{c}}\right)f_{0}$	$\Delta f={\frac {\Delta v}{c}}f_{0}$

where

\Delta f=f-f_{0}\,

\Delta v=v_{\text{r}}-v_{\text{s}}\,

is the velocity of the receiver relative to the source: it is positive when the source and the receiver are moving towards each other.

Proof

Given $f=\left({\frac {c+v_{\text{r}}}{c+v_{\text{s}}}}\right)f_{0}\,$

we divide for $c$

$f=\left({\frac {1+{\frac {v_{\text{r}}}{c}}}{1+{\frac {v_{\text{s}}}{c}}}}\right)f_{0}=\left(1+{\frac {v_{\text{r}}}{c}}\right)\left({\frac {1}{1+{\frac {v_{\text{s}}}{c}}}}\right)f_{0}\,$

Since ${\frac {v_{\text{s}}}{c}}\ll 1$ we can substitute the geometric expansion:

${\frac {1}{1+{\frac {v_{\text{s}}}{c}}}}\approx 1-{\frac {v_{\text{s}}}{c}}$

Analysis

The frequency of the sounds that the source emits does not actually change. To understand what happens, consider the following analogy. Someone throws one ball every second in a man's direction. Assume that balls travel with constant velocity. If the thrower is stationary, the man will receive one ball every second. However, if the thrower is moving towards the man, he will receive balls more frequently because the balls will be less spaced out. The inverse is true if the thrower is moving away from the man. So it is actually the wavelength which is affected; as a consequence, the received frequency is also affected. It may also be said that the velocity of the wave remains constant whereas wavelength changes; hence frequency also changes.

With an observer stationary relative to the medium, if a moving source is emitting waves with an actual frequency $f_{\text{0}}$ (in this case, the wavelength is changed, the transmission velocity of the wave keeps constant ${\text{--}}$ note that the transmission velocity of the wave does not depend on the velocity of the source), then the observer detects waves with a frequency $f$ given by

f=\left({\frac {c}{c+v_{\text{s}}}}\right)f_{0}

A similar analysis for a moving observer and a stationary source (in this case, the wavelength keeps constant, but due to the motion, the rate at which the observer receives waves ${\text{--}}$ and hence the transmission velocity of the wave [with respect to the observer] ${\text{--}}$ is changed) yields the observed frequency:

f=\left({\frac {c+v_{\text{r}}}{c}}\right)f_{0}

These can be generalized into the equation that was presented in the previous section.

f=\left({\frac {c+v_{\text{r}}}{c+v_{\text{s}}}}\right)f_{0}

An interesting effect was predicted by Lord Rayleigh in his classic book on sound: if the source is moving at twice the speed of sound, a musical piece emitted by that source would be heard in correct time and tune, but backwards.^[6]

Application

Sirens

The siren on a passing emergency vehicle will start out higher than its stationary pitch, slide down as it passes, and continue lower than its stationary pitch as it recedes from the observer. Astronomer John Dobson explained the effect thus:

"The reason the siren slides is because it doesn't hit you."

In other words, if the siren approached the observer directly, the pitch would remain constant until the vehicle hit him, and then immediately jump to a new lower pitch. Because the vehicle passes by the observer, the radial velocity does not remain constant, but instead varies as a function of the angle between his line of sight and the siren's velocity:

v_{\text{radial}}=v_{\text{s}}\cdot \cos {\theta }

where $\theta$ is the angle between the object's forward velocity and the line of sight from the object to the observer.

Astronomy

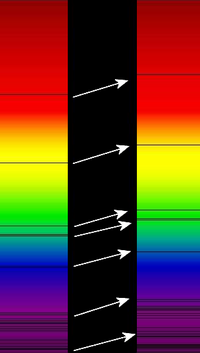
Redshift of spectral lines in the optical spectrum of a supercluster of distant galaxies (right), as compared to that of the Sun (left)

The Doppler effect for electromagnetic waves such as light is of great use in astronomy and results in either a so-called redshift or blueshift. It has been used to measure the speed at which stars and galaxies are approaching or receding from us, that is, the radial velocity. This is used to detect if an apparently single star is, in reality, a close binary and even to measure the rotational speed of stars and galaxies.

The use of the Doppler effect for light in astronomy depends on our knowledge that the spectra of stars are not homogeneous. They exhibit absorption lines at well defined frequencies that are correlated with the energies required to excite electrons in various elements from one level to another. The Doppler effect is recognizable in the fact that the absorption lines are not always at the frequencies that are obtained from the spectrum of a stationary light source. Since blue light has a higher frequency than red light, the spectral lines of an approaching astronomical light source exhibit a blueshift and those of a receding astronomical light source exhibit a redshift.

Among the nearby stars, the largest radial velocities with respect to the Sun are +308 km/s (BD-15°4041, also known as LHS 52, 81.7 light-years away) and -260 km/s (Woolley 9722, also known as Wolf 1106 and LHS 64, 78.2 light-years away). Positive radial velocity means the star is receding from the Sun, negative that it is approaching.

Temperature measurement

Another use of the Doppler effect, which is found mostly in plasma physics and astronomy, is the estimation of the temperature of a gas (or ion temperature in a plasma) which is emitting a spectral line. Due to the thermal motion of the emitters, the light emitted by each particle can be slightly red- or blue-shifted, and the net effect is a broadening of the line. This line shape is called a Doppler profile and the width of the line is proportional to the square root of the temperature of the emitting species, allowing a spectral line (with the width dominated by the Doppler broadening) to be used to infer the temperature.

Radar

The Doppler effect is used in some types of radar, to measure the velocity of detected objects. A radar beam is fired at a moving target — e.g. a motor car, as police use radar to detect speeding motorists — as it approaches or recedes from the radar source. Each successive radar wave has to travel farther to reach the car, before being reflected and re-detected near the source. As each wave has to move farther, the gap between each wave increases, increasing the wavelength. In some situations, the radar beam is fired at the moving car as it approaches, in which case each successive wave travels a lesser distance, decreasing the wavelength. In either situation, calculations from the Doppler effect accurately determine the car's velocity. Moreover, the proximity fuze, developed during World War II, relies upon Doppler radar to detonate explosives at the correct time, height, distance, etc.^{[citation needed]}

Medical imaging and blood flow measurement

Colour flow ultrasonography (Doppler) of a carotid artery - scanner and screen

An echocardiogram can, within certain limits, produce accurate assessment of the direction of blood flow and the velocity of blood and cardiac tissue at any arbitrary point using the Doppler effect. One of the limitations is that the ultrasound beam should be as parallel to the blood flow as possible. Velocity measurements allow assessment of cardiac valve areas and function, any abnormal communications between the left and right side of the heart, any leaking of blood through the valves (valvular regurgitation), and calculation of the cardiac output. Contrast-enhanced ultrasound using gas-filled microbubble contrast media can be used to improve velocity or other flow-related medical measurements.

Although "Doppler" has become synonymous with "velocity measurement" in medical imaging, in many cases it is not the frequency shift (Doppler shift) of the received signal that is measured, but the phase shift (when the received signal arrives).

Velocity measurements of blood flow are also used in other fields of medical ultrasonography, such as obstetric ultrasonography and neurology. Velocity measurement of blood flow in arteries and veins based on Doppler effect is an effective tool for diagnosis of vascular problems like stenosis.^[7]

Flow measurement

Instruments such as the laser Doppler velocimeter (LDV), and acoustic Doppler velocimeter (ADV) have been developed to measure velocities in a fluid flow. The LDV emits a light beam and the ADV emits an ultrasonic acoustic burst, and measure the Doppler shift in wavelengths of reflections from particles moving with the flow. The actual flow is computed as a function of the water velocity and phase. This technique allows non-intrusive flow measurements, at high precision and high frequency.

Velocity profile measurement

Developed originally for velocity measurements in medical applications (blood flow), Ultrasonic Doppler Velocimetry (UDV) can measure in real time complete velocity profile in almost any liquids containing particles in suspension such as dust, gas bubbles, emulsions. Flows can be pulsating, oscillating, laminar or turbulent, stationary or transient. This technique is fully non-invasive.

Satellite communication

Fast moving satellites can have a Doppler shift of dozens of kilohertz relative to a ground station. The speed, thus magnitude of Doppler effect, changes due to earth curvature. Dynamic Doppler compensation, where the frequency of a signal is changed multiple times during transmission, is used so the satellite receives a constant frequency signal.^[8]

Underwater acoustics

In military applications the Doppler shift of a target is used to ascertain the speed of a submarine using both passive and active sonar systems. As a submarine passes by a passive sonobuoy, the stable frequencies undergo a Doppler shift, and the speed and range from the sonobuoy can be calculated. If the sonar system is mounted on a moving ship or another submarine, then the relative velocity can be calculated.

Audio

The Leslie speaker, associated with and predominantly used with the Hammond B-3 organ, takes advantage of the Doppler Effect by using an electric motor to rotate an acoustic horn around a loudspeaker, sending its sound in a circle. This results at the listener's ear in rapidly fluctuating frequencies of a keyboard note.

Vibration measurement

A laser Doppler vibrometer (LDV) is a non-contact method for measuring vibration. The laser beam from the LDV is directed at the surface of interest, and the vibration amplitude and frequency are extracted from the Doppler shift of the laser beam frequency due to the motion of the surface.

Passing car horn

Problems playing this file? See media help.

References

Doppler, C. J. (1842). Über das farbige Licht der Doppelsterne und einiger anderer Gestirne des Himmels (About the coloured light of the binary stars and some other stars of the heavens). Publisher: Abhandlungen der Königl. Böhm. Gesellschaft der Wissenschaften (V. Folge, Bd. 2, S. 465-482) [Proceedings of the Royal Bohemian Society of Sciences (Part V, Vol 2)]; Prague: 1842 (Reissued 1903). Some sources mention 1843 as year of publication because in that year the article was published in the Proceedings of the Bohemian Society of Sciences. Doppler himself referred to the publication as "Prag 1842 bei Borrosch und André", because in 1842 he had a preliminary edition printed that he distributed independently.

^ Alec Eden The search for Christian Doppler,Springer-Verlag, Wien 1992. Contains a facsimile edition with an English translation.
^ Buys Ballot (1845). "Akustische Versuche auf der Niederländischen Eisenbahn, nebst gelegentlichen Bemerkungen zur Theorie des Hrn. Prof. Doppler (in German)". Annalen der Physik und Chemie. 11: 321–351.
^
Fizeau: "Acoustique et optique". Lecture, Société Philomathique de Paris, 29 December 1848. According to Becker(pg. 109), this was never published, but recounted by M. Moigno(1850): "Répertoire d'optique moderne" (in French), vol 3. pp 1165-1203 and later in full by Fizeau, "Des effets du mouvement sur le ton des vibrations sonores et sur la longeur d'onde des rayons de lumière"; [Paris, 1870]. Annales de Chimie et de Physique, 19, 211-221.
- Becker (2011). Barbara J. Becker, Unravelling Starlight: William and Margaret Huggins and the Rise of the New Astronomy, illustrated Edition, Cambridge University Press, 2011; ISBN 110700229X, 9781107002296.
^ Scott Russell, John (1848). "On certain effects produced on sound by the rapid motion of the observer". Report of the Eighteen Meeting of the British Association for the Advancement of Science. 18 (7). John Murray, London in 1849: 37–38. Retrieved 2008-07-08.
^ ^a ^b Rosen, Joe; Gothard, Lisa Quinn (2009). Encyclopedia of Physical Science. Infobase Publishing. p. 155. ISBN 0-8160-7011-3., Extract of page 155
^ Strutt (Lord Rayleigh), John William (1896). MacMillan & Co (ed.). The Theory of Sound. Vol. 2 (2 ed.). p. 154.
^ Evans, D. H.; McDicken, W. N. (2000). Doppler Ultrasound (Second ed.). New York: John Wiley and Sons. ISBN 0-471-97001-8.
^ Qingchong, Liu (1999), "Doppler measurement and compensation in mobile satellite communications systems", Military Communications Conference Proceedings / MILCOM, 1: 316–320

External links

Doppler Effect, [ScienceWorld]
Java simulation of Doppler effect
Doppler Shift for Sound and Light at MathPages
Flash simulation and game of Doppler effect of sound at Scratch (programming language)
The Doppler Effect and Sonic Booms (D.A. Russell, Kettering University)
Video Mashup with Doppler Effect videos
Wave Propagation from John de Pillis. An animation showing that the speed of a moving wave source does not affect the speed of the wave.
EM Wave Animation from John de Pillis. How an electromagnetic wave propagates through a vacuum
Doppler Shift Demo - Interactive flash simulation for demonstrating Doppler shift.
Interactive applets at Physics 2000

Template:Link FA

[AlecEden-1] Alec Eden The search for Christian Doppler,Springer-Verlag, Wien 1992. Contains a facsimile edition with an English translation.

[2] Buys Ballot (1845). "Akustische Versuche auf der Niederländischen Eisenbahn, nebst gelegentlichen Bemerkungen zur Theorie des Hrn. Prof. Doppler (in German)". Annalen der Physik und Chemie. 11: 321–351.

[3] Fizeau: "Acoustique et optique". Lecture, Société Philomathique de Paris, 29 December 1848. According to Becker(pg. 109), this was never published, but recounted by M. Moigno(1850): "Répertoire d'optique moderne" (in French), vol 3. pp 1165-1203 and later in full by Fizeau, "Des effets du mouvement sur le ton des vibrations sonores et sur la longeur d'onde des rayons de lumière"; [Paris, 1870]. Annales de Chimie et de Physique, 19, 211-221.
Becker (2011). Barbara J. Becker, Unravelling Starlight: William and Margaret Huggins and the Rise of the New Astronomy, illustrated Edition, Cambridge University Press, 2011; ISBN 110700229X, 9781107002296.

[4] Becker (2011). Barbara J. Becker, Unravelling Starlight: William and Margaret Huggins and the Rise of the New Astronomy, illustrated Edition, Cambridge University Press, 2011; ISBN 110700229X, 9781107002296.

[4] Scott Russell, John (1848). "On certain effects produced on sound by the rapid motion of the observer". Report of the Eighteen Meeting of the British Association for the Advancement of Science. 18 (7). John Murray, London in 1849: 37–38. Retrieved 2008-07-08.

[encphysci-5] Rosen, Joe; Gothard, Lisa Quinn (2009). Encyclopedia of Physical Science. Infobase Publishing. p. 155. ISBN 0-8160-7011-3., Extract of page 155

[6] Strutt (Lord Rayleigh), John William (1896). MacMillan & Co (ed.). The Theory of Sound. Vol. 2 (2 ed.). p. 154.

[7] Evans, D. H.; McDicken, W. N. (2000). Doppler Ultrasound (Second ed.). New York: John Wiley and Sons. ISBN 0-471-97001-8.

[8] Qingchong, Liu (1999), "Doppler measurement and compensation in mobile satellite communications systems", Military Communications Conference Proceedings / MILCOM, 1: 316–320

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

@@ Line 54: / Line 54: @@
 The above formula assumes that the source is either directly approaching or receding from the observer. If the source approaches the observer at an angle (but still with a constant velocity), the observed frequency that is first heard is higher than the object's emitted frequency. Thereafter, there is a [[monotonic]] decrease in the observed frequency as it gets closer to the observer, through equality when it is coming from a direction perpendicular to the relative motion (and was emitted at the point of closest approach; but when the wave is received, the source and observer will no longer be at their closest), and a continued monotonic decrease as it recedes from the observer. When the observer is very close to the path of the object, the transition from high to low frequency is very abrupt. When the observer is far from the path of the object, the transition from high to low frequency is gradual.
-If the speeds Vs and Vr are small compared to the speed of the wave, the relationship between observed frequency f and emitted frequency fo is approximately<ref name=encphysci />
+If the speeds <math>v_\text{s} \,</math> and <math>v_\text{r} \,</math> are small compared to the speed of the wave, the relationship between observed frequency <math>f</math> and emitted frequency <math>f_\text{0}</math> is approximately<ref name=encphysci />
 {|
 |-
@@ Line 78: / Line 78: @@
 {{Collapse bottom}}
+==Analysis==
+The frequency of the sounds that the source ''emits'' does not actually change. To understand what happens, consider the following analogy. Someone throws one ball every second in a man's direction. Assume that balls travel with constant velocity. If the thrower is stationary, the man will receive one ball every second. However, if the thrower is moving towards the man, he will receive balls more frequently because the balls will be less spaced out. The inverse is true if the thrower is moving away from the man. So it is actually the ''wavelength'' which is affected; as a consequence, the received frequency is also affected. It may also be said that the velocity of the wave remains constant whereas wavelength changes; hence frequency also changes.
+With an observer stationary relative to the medium, if a moving source is emitting waves with an actual frequency <math>f_\text{0}</math> (in this case, the wavelength is changed, the transmission velocity of the wave keeps constant <math>\text{--}</math> note that the ''transmission velocity'' of the wave does not depend on the ''velocity of the source''), then the observer detects waves with a frequency <math>f</math> given by
+:<math>f = \left ( \frac {c}{c + v_\text{s}} \right ) f_0</math>
-Analysis
+A similar analysis for a moving ''observer'' and a stationary source (in this case, the wavelength keeps constant, but due to the motion, the rate at which the observer receives waves <math>\text{--}</math> and hence the ''transmission velocity'' of the wave [with respect to the observer] <math>\text{--}</math> is changed) yields the observed frequency:
-The frequency of the sounds that the source emits does not actually change. To understand what happens, consider the following analogy. Someone throws one ball every second in a man's direction. Assume that balls travel with constant velocity. If the thrower is stationary, the man will receive one ball every second. However, if the thrower is moving towards the man, he will receive balls more frequently because the balls will be less spaced out. The inverse is true if the thrower is moving away from the man. So it is actually the wavelength which is affected; as a consequence, the received frequency is also affected. It may also be said that the velocity of the wave remains constant whereas wavelength changes; hence frequency also changes.
+:<math>f = \left ( \frac {c + v_\text{r}}{c} \right ) f_0</math>
-With an observer stationary relative to the medium, if a moving source is emitting waves with an actual frequency f_\text{0} (in this case, the wavelength is changed, the transmission velocity of the wave keeps constant \text{--} note that the transmission velocity of the wave does not depend on the velocity of the source), then the observer detects waves with a frequency f given by
-    f =(c/c+Vs) f_0
-A similar analysis for a moving observer and a stationary source (in this case, the wavelength keeps constant, but due to the motion, the rate at which the observer receives waves \text{--} and hence the transmission velocity of the wave [with respect to the observer] \text{--} is changed) yields the observed frequency:
-   f=(c+Vr/C)fo
 These can be generalized into the equation that was presented in the previous section.
-    f = \left ( \frac {c+v_\text{r}}{c + v_\text{s}} \right ) f_0
+:<math>f = \left ( \frac {c+v_\text{r}}{c + v_\text{s}} \right ) f_0</math><center>
-An interesting effect was predicted by Lord Rayleigh in his classic book on sound: if the source is moving at twice the speed of sound, a musical piece emitted by that source would be heard in correct time and tune, but backwards.[6]
+An interesting effect was predicted by Lord Rayleigh in his classic book on sound: if the source is moving at twice the speed of sound, a musical piece emitted by that source would be heard in correct time and tune, but ''backwards''.<ref>{{cite book|last=Strutt (Lord Rayleigh)|first=John William|title=The Theory of Sound|editor=MacMillan & Co|year=1896|edition=2|volume=2|pages=154|url=http://archive.org/stream/theorysound02raylgoog#page/n176/mode/2up}}</ref>
 ==Application==
@@ Line 154: / Line 152: @@
 {{Listen|filename=Speeding-car-horn_doppler_effect_sample.ogg|title=Passing car horn|format=[[Ogg]]}}
+==See also==
+* [[Relativistic Doppler effect]]
+* [[Dopplergraph]]
+* [[Fizeau experiment]]
+* [[Fading]]
+* [[Inverse Doppler effect]]
+* [[Photoacoustic Doppler effect]]
+* [[Differential Doppler effect]]
+* [[Rayleigh fading]]
+== References ==
+* Doppler, C. J. (1842). <small> [[Über das farbige Licht der Doppelsterne und einiger anderer Gestirne des Himmels|Über das farbige Licht der Doppelsterne und einiger anderer Gestirne des Himmels (About the coloured light of the binary stars and some other stars of the heavens)]]. Publisher: Abhandlungen der Königl. Böhm. Gesellschaft der Wissenschaften (V. Folge, Bd. 2, S. 465-482) [Proceedings of the Royal Bohemian Society of Sciences (Part V, Vol 2)]; Prague: 1842 (Reissued 1903). Some sources mention 1843 as year of publication because in that year the article was published in the Proceedings of the Bohemian Society of Sciences. Doppler himself referred to the publication as "Prag 1842 bei Borrosch und André", because in 1842 he had a preliminary edition printed that he distributed independently.</small>
+{{reflist}}
+==Further reading==
+* "Doppler and the Doppler effect", E. N. da C. Andrade, ''Endeavour'' Vol. XVIII No. 69, January 1959 (published by ICI London). Historical account of Doppler's original paper and subsequent developments.
+* {{cite web | url = http://archive.ncsa.uiuc.edu/Cyberia/Bima/doppler.html | title = Doppler Effect | first = Eleni | last = Adrian | publisher = [[National Center for Supercomputing Applications|NCSA]] | date = 24 June 1995 | accessdate = 2008-07-13 }}
+==External links==
+{{Commons}}
+* [http://scienceworld.wolfram.com/physics/DopplerEffect.html Doppler Effect], [ScienceWorld]
+* [http://www.falstad.com/ripple/ex-doppler.html Java simulation of Doppler effect]
+* [http://www.mathpages.com/rr/s2-04/2-04.htm Doppler Shift for Sound and Light] at MathPages
+* [http://scratch.mit.edu/projects/12532039/ Flash simulation and game of Doppler effect of sound] at [[Scratch (programming language)]]
+* [http://www.kettering.edu/~drussell/Demos/doppler/doppler.html The Doppler Effect and Sonic Booms (D.A. Russell, Kettering University)]
+* [http://beta.vtap.com/video/Doppler+Effect/CL0113709540_1d645df0e Video Mashup with Doppler Effect videos]
+* [http://math.ucr.edu/~jdp/Relativity/WaveDancer.html Wave Propagation] ''from John de Pillis.'' An animation showing that the speed of a moving wave source does not affect the speed of the wave.
+* [http://math.ucr.edu/~jdp/Relativity/EM_Propagation.html EM Wave Animation] ''from John de Pillis.'' How an electromagnetic wave propagates through a vacuum
+* [http://astro.unl.edu/classaction/animations/light/dopplershift.html Doppler Shift Demo] - Interactive flash simulation for demonstrating Doppler shift.
+*[http://www.colorado.edu/physics/2000/applets_New.html Interactive applets] at Physics 2000
+{{DEFAULTSORT:Doppler Effect}}
+[[Category:Doppler effects]]
+[[Category:Radio frequency propagation]]
+[[Category:Wave mechanics]]
+[[Category:Radar signal processing]]
+{{link FA|pl}}