Fourier series: Difference between revisions
←Replaced content with 'It's just maths.' Tag: blanking |
ClueBot NG (talk | contribs) m Reverting possible vandalism by 176.251.99.144 to version by WangPublic. False positive? Report it. Thanks, ClueBot NG. (1732475) (Bot) |
||
| Line 1: | Line 1: | ||
{{Fourier transforms}} |
|||
It's just maths. |
|||
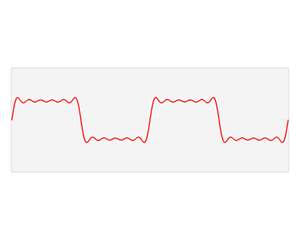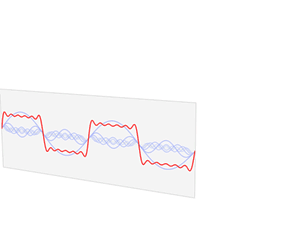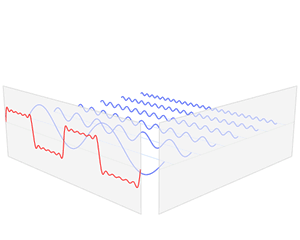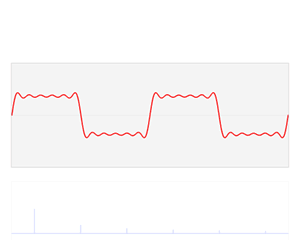
[[File:Fourier Series.svg|thumb|right|180px|The first four partial sums of the Fourier series for a [[square wave]]]] |
|||
In [[mathematics]], a '''Fourier series''' ({{IPAc-en|lang|pron|ˈ|f|ɔər|i|eɪ}}) decomposes [[periodic function]]s or periodic signals into the sum of a (possibly infinite) set of simple oscillating functions, namely [[sine wave|sines and cosines]] (or [[complex exponential]]s). The study of Fourier series is a branch of [[Fourier analysis]]. |
|||
__TOC__ |
|||
{{Clear}} |
|||
==History== |
|||
The Fourier series is named in honour of [[Jean-Baptiste Joseph Fourier]] (1768–1830), who made important contributions to the study of [[trigonometric series]], after preliminary investigations by [[Leonhard Euler]], [[Jean le Rond d'Alembert]], and [[Daniel Bernoulli]].<ref group="nb">These three did some [[wave equation#Notes|important early work on the wave equation]], especially D'Alembert. Euler's work in this area was mostly [[Euler-Bernoulli beam equation|comtemporaneous/ in collaboration with Bernoulli]], although the latter made some independent contributions to the theory of waves and vibrations ([http://books.google.co.uk/books?id=olMpStYOlnoC&pg=PA214&lpg=PA214&dq=bernoulli+solution+wave+equation&source=bl&ots=h8eN69CWRm&sig=lRq2-8FZvcXIjToXQI4k6AVfRqA&hl=en&sa=X&ei=RqOhUIHOIOa00QWZuIHgCw&ved=0CCEQ6AEwATg8#v=onepage&q=bernoulli%20solution%20wave%20equation&f=false see here, pg.s 209 & 210, ]).</ref> Fourier introduced the series for the purpose of solving the [[heat equation]] in a metal plate, publishing his initial results in his 1807 ''[[Mémoire sur la propagation de la chaleur dans les corps solides]]'' (''Treatise on the propagation of heat in solid bodies''), and publishing his ''Théorie analytique de la chaleur'' in 1822. Early ideas of decomposing a periodic function into the sum of simple oscillating functions date back to the 3rd century BC, when ancient astronomers proposed an empiric model of planetary motions, based on [[Deferent and epicycle|deferents and epicycles]]. |
|||
The heat equation is a [[partial differential equation]]. Prior to Fourier's work, no solution to the heat equation was known in the general case, although particular solutions were known if the heat source behaved in a simple way, in particular, if the heat source was a [[sine]] or [[cosine]] wave. These simple solutions are now sometimes called [[Eigenvalue, eigenvector and eigenspace|eigensolutions]]. Fourier's idea was to model a complicated heat source as a superposition (or [[linear combination]]) of simple sine and cosine waves, and to write the [[superposition principle|solution as a superposition]] of the corresponding [[eigenfunction|eigensolutions]]. This superposition or linear combination is called the Fourier series. |
|||
From a modern point of view, Fourier's results are somewhat informal, due to the lack of a precise notion of [[function (mathematics)|function]] and [[integral]] in the early nineteenth century. Later, [[Peter Gustav Lejeune Dirichlet]]<ref>Lejeune-Dirichlet, P. "[[List of important publications in mathematics#Sur la convergence des séries trigonométriques qui servent à représenter une fonction arbitraire entre des limites données|Sur la convergence des séries trigonométriques qui servent à représenter une fonction arbitraire entre des limites données]]". (In French), transl. "On the convergence of trigonometric series which serve to represent an arbitrary function between two given limits". Journal f¨ur die reine und angewandte Mathematik, Vol. 4 (1829) p. 157–169.</ref> and [[Bernhard Riemann]]<ref>{{cite web|url = http://www.maths.tcd.ie/pub/HistMath/People/Riemann/Trig/| title=Ueber die Darstellbarkeit einer Function durch eine trigonometrische Reihe |language=German|work=[[Habilitationschrift]], [[Göttingen]]; 1854. Abhandlungen der [[Göttingen Academy of Sciences|Königlichen Gesellschaft der Wissenschaften zu Göttingen]], vol. 13, 1867''. Published posthumously for Riemann by [[Richard Dedekind]]|trans_title=About the representability of a function by a trigonometric series|accessdate= 19 May 2008 <!--DASHBot-->| archiveurl= http://web.archive.org/web/20080520085248/http://www.maths.tcd.ie/pub/HistMath/People/Riemann/Trig/ | archivedate= 20 May 2008| deadurl= no}}</ref><ref>D. Mascre, Bernhard Riemann: Posthumous Thesis on the Representation of Functions by Triginometric Series (1867). [http://books.google.co.uk/books?id=UdGBy8iLpocC&printsec=frontcover#v=onepage&q&f=false Landmark Writings in Western Mathematics 1640–1940], Ivor Grattan-Guinness (ed.); pg. 492. Elsevier, 20 May 2005.Accessed 7 Dec 2012.</</ref><ref>[http://books.google.co.uk/books?id=uP8SF4jf7GEC&printsec=frontcover#v=onepage&q&f=false Theory of Complex Functions: Readings in Mathematics], by Reinhold Remmert; pg 29. Springer, 1991. Accessed 7 Dec 2012.</ref> expressed Fourier's results with greater precision and formality. |
|||
Although the original motivation was to solve the heat equation, it later became obvious that the same techniques could be applied to a wide array of mathematical and physical problems, and especially those involving linear differential equations with constant coefficients, for which the eigensolutions are [[Sine wave|sinusoid]]s. The Fourier series has many such applications in [[electrical engineering]], [[oscillation|vibration]] analysis, [[acoustics]], [[optics]], [[signal processing]], [[image processing]], [[quantum mechanics]], [[econometrics]],<ref>{{cite book |first=Marc |last=Nerlove |first2=David M. |last2=Grether |first3=Jose L. |last3=Carvalho |year=1995 |title=Analysis of Economic Time Series. Economic Theory, Econometrics, and Mathematical Economics |location= |publisher=Elsevier |isbn=0-12-515751-7 }}</ref> [[Thin-shell structure|thin-walled shell]] theory,<ref>{{cite book |first=Wilhelm |last=Flugge |year=1957 |title=Statik und Dynamik der Schalen |publisher=Springer-Verlag |location=Berlin }}</ref> etc. |
|||
==Definition== |
|||
In this section, ''s''(''x'') denotes a function of the real variable ''x'', and ''s'' is integrable on an interval [''x''<sub>0</sub>, ''x''<sub>0</sub> + ''P''], for real numbers ''x''<sub>0</sub> and ''P''. We will attempt to represent ''s'' in that interval as an infinite sum, or [[series (mathematics)|series]], of harmonically related sinusoidal functions. Outside the interval, the series is periodic with period ''P'' (frequency 1/''P''). It follows that if ''s'' also has that property, the approximation is valid on the entire real line. We can begin with a finite summation (or ''partial sum'')''':''' |
|||
:<math>s_N(x) = \frac{a_0}{2} + \sum_{n=1}^N A_n\cdot \sin(\tfrac{2\pi nx}{P}+\phi_n), \quad \scriptstyle \text{for integer}\ N\ \ge\ 1.</math> |
|||
<math>s_N(x)</math> is a periodic function with period '''P'''. Using the identities''':''' |
|||
:<math>\sin(\tfrac{2\pi nx}{P}+\phi_n) \equiv \sin(\phi_n) \cos(\tfrac{2\pi nx}{P}) + \cos(\phi_n) \sin(\tfrac{2\pi nx}{P})</math> |
|||
:<math>\sin(\tfrac{2\pi nx}{P}+\phi_n) \equiv \text{Re}\left\{\frac{1}{i}\cdot e^{i \left(\tfrac{2\pi nx}{P}+\phi_n\right)}\right\} = \frac{1}{2i}\cdot e^{i \left(\tfrac{2\pi nx}{P}+\phi_n\right)} +\left(\frac{1}{2i}\cdot e^{i \left(\tfrac{2\pi nx}{P}+\phi_n\right)}\right)^*,</math> |
|||
[[File:Fourier series and transform.gif|frame|right|Function ''s''(''x'') (in red) is a sum of six sine functions of different amplitudes and harmonically related frequencies. Their summation is called a Fourier series. The Fourier transform, ''S''(''f'') (in blue), which depicts amplitude vs frequency, reveals the 6 frequencies and their amplitudes.]] |
|||
we can also write the function in these equivalent forms''':''' |
|||
{| class="wikitable" style="text-align:left" |
|||
|<math> |
|||
\begin{align} |
|||
s_N(x) &= \frac{a_0}{2} + \sum_{n=1}^N \left(\overbrace{a_n}^{A_n \sin(\phi_n)} \cos(\tfrac{2\pi nx}{P}) + \overbrace{b_n}^{A_n \cos(\phi_n)} \sin(\tfrac{2\pi nx}{P})\right)\\ |
|||
&= \sum_{n=-N}^N c_n\cdot e^{i \tfrac{2\pi nx}{P}}, |
|||
\end{align} |
|||
</math> |
|||
|} |
|||
where''':''' |
|||
:<math> |
|||
c_n \ \stackrel{\mathrm{def}}{=} \ \begin{cases} |
|||
\frac{A_n}{2i} e^{i\phi_n} = \frac{1}{2}(a_n - i b_n) & \text{for } n > 0 \\ |
|||
\frac{1}{2}a_0 & \text{for }n = 0\\ |
|||
c_{|n|}^* & \text{for } n < 0. |
|||
\end{cases} |
|||
</math> |
|||
When the coefficients (known as '''Fourier coefficients''') are computed as follows''':'''<ref> |
|||
{{cite book |
|||
| last1 = Dorf| first1 = Richard C. |
|||
| first2 = Ronald J. | last2 = Tallarida |
|||
| title =Pocket Book of Electrical Engineering Formulas |
|||
| publisher =CRC Press |
|||
| edition =1 |
|||
| date =1993-07-15 |
|||
| location =Boca Raton,FL |
|||
| pages =171–174 |
|||
| isbn =0849344735 }}</ref> |
|||
:{| |
|||
|<math>a_n = \frac{2}{P}\int_{x_0}^{x_0+P} s(x)\cdot \cos(\tfrac{2\pi nx}{P})\ dx</math><br> |
|||
<math>b_n = \frac{2}{P}\int_{x_0}^{x_0+P} s(x)\cdot \sin(\tfrac{2\pi nx}{P})\ dx</math> |
|||
| <math>c_n = \frac{1}{P}\int_{x_0}^{x_0+P} s(x)\cdot e^{-i \tfrac{2\pi nx}{P}}\ dx,</math> |
|||
|} |
|||
<math>s_N(x)</math> approximates <math>\scriptstyle s(x)</math> on <math>\scriptstyle [x_0,\ x_0+P],</math> and the approximation improves as ''N'' → ∞. The [[Series (mathematics)#Formal definition|infinite sum]], <math>\scriptstyle s_{\infty}(x),</math> is called the '''Fourier series''' representation of <math>s.</math> In [[engineering]] applications, the Fourier series is generally presumed to converge everywhere except at discontinuities, since the functions encountered in engineering are more well behaved than the ones that mathematicians can provide as counter-examples to this presumption. In particular, the Fourier series converges absolutely and uniformly to ''s''(''x'') whenever the derivative of ''s''(''x'') (which may not exist everywhere) is square integrable.<ref>{{cite book | title = Fourier Series | author = Georgi P. Tolstov | publisher = Courier-Dover | year = 1976 | isbn = 0-486-63317-9 | url = http://books.google.com/?id=XqqNDQeLfAkC&pg=PA82&dq=fourier-series+converges+continuous-function }}</ref> If a function is [[Square-integrable function|square-integrable]] on the interval [x<sub>0</sub>, x<sub>0</sub>+P], then the Fourier series converges to the function at ''[[almost every]]'' point. See [[Convergence of Fourier series]]. It is possible to define Fourier coefficients for more general functions or distributions, in such cases convergence in norm or [[Weak convergence (Hilbert space)|weak convergence]] is usually of interest. |
|||
===Example 1: a simple Fourier series=== |
|||
[[File:sawtooth 2pi.gif|thumb|right|400px|Plot of a periodic identity function, a [[sawtooth wave]]]] |
|||
[[File:Periodic identity function.gif|thumb|right|400px|Animated plot of the first five successive partial Fourier series]] |
|||
We now use the formula above to give a Fourier series expansion of a very simple function. Consider a sawtooth wave |
|||
:<math>s(x) = \frac{x}{\pi}, \quad \mathrm{for } -\pi < x < \pi,</math> |
|||
:<math>s(x + 2\pi k) = s(x), \quad \mathrm{for } -\infty < x < \infty \text{ and } k \in \mathbb{Z} .</math> |
|||
In this case, the Fourier coefficients are given by |
|||
:<math>\begin{align} |
|||
a_n &{} = \frac{1}{\pi}\int_{-\pi}^{\pi}s(x) \cos(nx)\,dx = 0, \quad n \ge 0. \\ |
|||
b_n &{} = \frac{1}{\pi}\int_{-\pi}^{\pi}s(x) \sin(nx)\, dx\\ |
|||
&= -\frac{2}{\pi n}\cos(n\pi) + \frac{2}{\pi^2 n^2}\sin(n\pi)\\ |
|||
&= \frac{2\,(-1)^{n+1}}{\pi n}, \quad n \ge 1.\end{align}</math> |
|||
It can be proven that the Fourier series converges to ''s''(''x'') at every point ''x'' where ''s'' is differentiable, and therefore: |
|||
{{NumBlk|: |
|||
|<math>\begin{align} |
|||
s(x) &= \frac{a_0}{2} + \sum_{n=1}^\infty \left[a_n\cos\left(nx\right)+b_n\sin\left(nx\right)\right] \\ |
|||
&=\frac{2}{\pi}\sum_{n=1}^\infty \frac{(-1)^{n+1}}{n} \sin(nx), \quad \mathrm{for} \quad x - \pi \notin 2 \pi \mathbf{Z}. |
|||
\end{align}</math> |
|||
|{{EquationRef|Eq.1}}}} |
|||
When ''x'' = π, the Fourier series converges to 0, which is the half-sum of the left- and right-limit of ''s'' at ''x'' = π. This is a particular instance of the [[Convergence of Fourier series#Convergence at a given point|Dirichlet theorem]] for Fourier series. |
|||
[[File:Fourier heat in a plate.png|thumb|right|Heat distribution in a metal plate, using Fourier's method]] |
|||
===Example 2: Fourier's motivation=== |
|||
The Fourier series expansion of our function in example 1 looks much less simple than the formula ''s''(''x'') = ''x/π'', and so it is not immediately apparent why one would need this Fourier series. While there are many applications, we cite Fourier's motivation of solving the heat equation. For example, consider a metal plate in the shape of a square whose side measures ''π'' meters, with coordinates (''x'', ''y'') ∈ [0, ''π''] × [0, ''π'']. If there is no heat source within the plate, and if three of the four sides are held at 0 degrees Celsius, while the fourth side, given by ''y'' = π, is maintained at the temperature gradient ''T''(''x'', ''π'') = ''x'' degrees Celsius, for ''x'' in (0, ''π''), then one can show that the stationary heat distribution (or the heat distribution after a long period of time has elapsed) is given by |
|||
: <math>T(x,y) = 2\sum_{n=1}^\infty \frac{(-1)^{n+1}}{n} \sin(nx) {\sinh(ny) \over \sinh(n\pi)}.</math> |
|||
Here, sinh is the [[hyperbolic sine]] function. This solution of the heat equation is obtained by multiplying each term of {{EquationNote|Eq.1}} by sinh(''ny'')/sinh(''n''π). While our example function ''s''(''x'') seems to have a needlessly complicated Fourier series, the heat distribution ''T''(''x'', ''y'') is nontrivial. The function ''T'' cannot be written as a [[closed-form expression]]. This method of solving the heat problem was made possible by Fourier's work. |
|||
===Other applications=== |
|||
Another application of this Fourier series is to solve the [[Basel problem]] by using [[Parseval's theorem]]. The example generalizes and one may compute [[Riemann zeta function|ζ]](2''n''), for any positive integer ''n''. |
|||
===Other common notations=== |
|||
The notation ''c''<sub>''n''</sub> is inadequate for discussing the Fourier coefficients of several different functions. Therefore it is customarily replaced by a modified form of the function (''s'', in this case), such as <math>\scriptstyle\hat{s}</math> or ''S'', and functional notation often replaces subscripting: |
|||
:<math>\begin{align} |
|||
s_{\infty}(x) &= \sum_{n=-\infty}^\infty \hat{s}(n)\cdot e^{i\tfrac{2\pi nx}{P}} \\ |
|||
&= \sum_{n=-\infty}^\infty S[n]\cdot e^{j\tfrac{2\pi nx}{P}} &&\scriptstyle \text{common engineering notation} |
|||
\end{align}</math> |
|||
In engineering, particularly when the variable ''x'' represents time, the coefficient sequence is called a [[frequency domain]] representation. Square brackets are often used to emphasize that the domain of this function is a discrete set of frequencies. |
|||
Another commonly used frequency domain representation uses the Fourier series coefficients to modulate a [[Dirac comb]]: |
|||
:<math>S(f) \ \stackrel{\mathrm{def}}{=} \ \sum_{n=-\infty}^\infty S[n]\cdot \delta \left(f-\frac{n}{P}\right),</math> |
|||
where ''f'' represents a continuous frequency domain. When variable ''x'' has units of seconds, ''f'' has units of [[hertz]]. The "teeth" of the comb are spaced at multiples (i.e. [[harmonics]]) of 1/P, which is called the [[fundamental frequency]]. <math>\scriptstyle s_{\infty}(x)</math> can be recovered from this representation by an [[Fourier inversion theorem|inverse Fourier transform]]: |
|||
:<math>\begin{align} |
|||
\mathcal{F}^{-1}\{S(f)\} &= \int_{-\infty}^\infty \left( \sum_{n=-\infty}^\infty S[n]\cdot \delta \left(f-\frac{n}{P}\right)\right) e^{i 2 \pi f x}\,df, \\ |
|||
&= \sum_{n=-\infty}^\infty S[n]\cdot \int_{-\infty}^\infty \delta\left(f-\frac{n}{P}\right) e^{i 2 \pi f x}\,df, \\ |
|||
&= \sum_{n=-\infty}^\infty S[n]\cdot e^{i\tfrac{2\pi nx}{P}} \ \ \stackrel{\mathrm{def}}{=} \ s_{\infty}(x). |
|||
\end{align}</math> |
|||
The constructed function ''S''(''f'') is therefore commonly referred to as a '''Fourier transform''', even though the Fourier integral of a periodic function is not convergent at the harmonic frequencies.<ref group="nb">Since the integral defining the Fourier transform of a periodic function is not convergent, it is necessary to view the periodic function and its transform as [[Distribution (mathematics)|distributions]]. In this sense <math>\mathcal{F} \left\{ e^{i \frac{2\pi nx}{P} } \right\}</math> is a [[Dirac delta function]], which is an example of a distribution.</ref> |
|||
==Beginnings== |
|||
{{cquote|<math>\varphi(y)=a_0\cos\frac{\pi y}{2}+a_1\cos 3\frac{\pi y}{2}+a_2\cos5\frac{\pi y}{2}+\cdots.</math> |
|||
Multiplying both sides by <math>\cos(2k+1)\frac{\pi y}{2}</math>, and then integrating from <math>y=-1</math> to <math>y=+1</math> yields: |
|||
: <math>a_k=\int_{-1}^1\varphi(y)\cos(2k+1)\frac{\pi y}{2}\,dy.</math> |
|||
|30px|30px|Joseph Fourier|[[Mémoire sur la propagation de la chaleur dans les corps solides]]. (1807)<ref>[http://gallica.bnf.fr/ark:/12148/bpt6k33707.image.r=Oeuvres+de+Fourier.f223.pagination.langFR Gallica - Fourier, Jean-Baptiste-Joseph (1768–1830). Oeuvres de Fourier. 1888, pp. 218–219,<!-- Bot generated title -->]</ref><ref group="nb">These words are not strictly Fourier's. Whilst the cited article does list the author as Fourier, a footnote indicates that the article was actually written by Poisson (that it was not written by Fourier is also clear from the consistent use of the third person to refer to him) and that it is, "for reasons of historical interest", presented as though it were Fourier's original memoire.</ref>}} |
|||
This immediately gives any coefficient ''a<sub>k</sub>'' of the trigonometrical series for φ(''y'') for any function which has such an expansion. It works because if φ has such an expansion, then (under suitable convergence assumptions) the integral |
|||
:<math>\begin{align} |
|||
a_k&=\int_{-1}^1\varphi(y)\cos(2k+1)\frac{\pi y}{2}\,dy \\ |
|||
&= \int_{-1}^1\left(a\cos\frac{\pi y}{2}\cos(2k+1)\frac{\pi y}{2}+a'\cos 3\frac{\pi y}{2}\cos(2k+1)\frac{\pi y}{2}+\cdots\right)\,dy |
|||
\end{align}</math> |
|||
can be carried out term-by-term. But all terms involving <math>\cos(2j+1)\frac{\pi y}{2} \cos(2k+1)\frac{\pi y}{2}</math> for {{nowrap|''j'' ≠ ''k''}} vanish when integrated from −1 to 1, leaving only the ''k''th term. |
|||
In these few lines, which are close to the modern [[Formalism (mathematics)|formalism]] used in Fourier series, Fourier revolutionized both mathematics and physics. Although similar trigonometric series were previously used by [[Euler]], [[d'Alembert]], [[Daniel Bernoulli]] and [[Carl Friedrich Gauss|Gauss]], Fourier believed that such trigonometric series could represent any arbitrary function. In what sense that is actually true is a somewhat subtle issue and the attempts over many years to clarify this idea have led to important discoveries in the theories of [[Convergent series|convergence]], [[function space]]s, and [[harmonic analysis]]. |
|||
When Fourier submitted a later competition essay in 1811, the committee (which included [[Joseph Louis Lagrange|Lagrange]], [[Laplace]], [[Étienne-Louis Malus|Malus]] and [[Adrien-Marie Legendre|Legendre]], among others) concluded: ''...the manner in which the author arrives at these equations is not exempt of difficulties and...his analysis to integrate them still leaves something to be desired on the score of generality and even [[Mathematical rigour|rigour]]''.{{citation needed|date=November 2012}} |
|||
===Birth of harmonic analysis=== |
|||
Since Fourier's time, many different approaches to defining and understanding the concept of Fourier series have been discovered, all of which are consistent with one another, but each of which emphasizes different aspects of the topic. Some of the more powerful and elegant approaches are based on mathematical ideas and tools that were not available at the time Fourier completed his original work. Fourier originally defined the Fourier series for real-valued functions of real arguments, and using the sine and cosine functions as the [[basis (linear algebra)|basis set]] for the decomposition. |
|||
Many other [[List of Fourier-related transforms|Fourier-related transforms]] have since been defined, extending the initial idea to other applications. This general area of inquiry is now sometimes called [[harmonic analysis]]. A Fourier series, however, can be used only for periodic functions, or for functions on a bounded (compact) interval. |
|||
==Extensions== |
|||
=== Fourier series on a square === |
|||
We can also define the Fourier series for functions of two variables ''x'' and ''y'' in the square [−π, π]×[−π, π]: |
|||
:<math>f(x,y) = \sum_{j,k \in \mathbf{Z}\text{ (integers)}} c_{j,k}e^{ijx}e^{iky},</math> |
|||
:<math>c_{j,k} = {1 \over 4 \pi^2} \int_{-\pi}^\pi \int_{-\pi}^\pi f(x,y) e^{-ijx}e^{-iky}\, dx \, dy.</math> |
|||
Aside from being useful for solving partial differential equations such as the heat equation, one notable application of Fourier series on the square is in [[image compression]]. In particular, the [[jpeg]] image compression standard uses the two-dimensional [[discrete cosine transform]], which is a Fourier transform using the cosine basis functions. |
|||
=== Fourier series of Bravais-lattice-periodic-function === |
|||
The [[Bravais lattice]] is defined as the set of vectors of the form: |
|||
:<math>\mathbf{R} = n_{1}\mathbf{a}_{1} + n_{2}\mathbf{a}_{2} + n_{3}\mathbf{a}_{3}</math> |
|||
where ''n<sub>i</sub>'' are integers and '''a'''<sub>''i''</sub> are three linearly independent vectors. Assuming we have some function, ''f''('''r'''), such that it obeys the following condition for any Bravais lattice vector '''R''': ''f''('''r''') = ''f''('''r''' + '''R'''), we could make a Fourier series of it. This kind of function can be, for example, the effective potential that one electron "feels" inside a periodic crystal. It is useful to make a Fourier series of the potential then when applying [[Bloch's Theorem|Bloch's theorem]]. First, we may write any arbitrary vector '''r''' in the coordinate-system of the lattice: |
|||
: <math>\mathbf{r} = x_1\frac{\mathbf{a}_{1}}{a_1}+ x_2\frac{\mathbf{a}_{2}}{a_2}+ x_3\frac{\mathbf{a}_{3}}{a_3},</math> |
|||
where ''a''<sub>''i''</sub> = |'''a'''<sub>''i''</sub>|. |
|||
Thus we can define a new function, |
|||
: <math>g(x_1,x_2,x_3) := f(\mathbf{r}) = f \left (x_1\frac{\mathbf{a}_{1}}{a_1}+x_2\frac{\mathbf{a}_{2}}{a_2}+x_3\frac{\mathbf{a}_{3}}{a_3} \right ).</math> |
|||
This new function, <math>g(x_1,x_2,x_3)</math>, is now a function of three-variables, each of which has periodicity ''a''<sub>1</sub>, ''a''<sub>2</sub>, ''a''<sub>3</sub> respectively: <math>g(x_1,x_2,x_3) = g(x_1+a_1,x_2,x_3) = g(x_1,x_2+a_2,x_3) = g(x_1,x_2,x_3+a_3)</math>. |
|||
If we write a series for ''g'' on the interval [0, ''a''<sub>1</sub>] for ''x''<sub>1</sub>, we can define the following: |
|||
:<math>h^\mathrm{one}(m_1, x_2, x_3) := \frac{1}{a_1}\int_0^{a_1} g(x_1, x_2, x_3)\cdot e^{-i 2\pi \frac{m_1}{a_1} x_1}\, dx_1</math> |
|||
And then we can write: |
|||
:<math>g(x_1, x_2, x_3)=\sum_{m_1=-\infty}^\infty h^\mathrm{one}(m_1, x_2, x_3) \cdot e^{i 2\pi \frac{m_1}{a_1} x_1}</math> |
|||
Further defining: |
|||
:<math> |
|||
\begin{align} |
|||
h^\mathrm{two}(m_1, m_2, x_3) & := \frac{1}{a_2}\int_0^{a_2} h^\mathrm{one}(m_1, x_2, x_3)\cdot e^{-i 2\pi \frac{m_2}{a_2} x_2}\, dx_2 \\[12pt] |
|||
& = \frac{1}{a_2}\int_0^{a_2} dx_2 \frac{1}{a_1}\int_0^{a_1} dx_1 g(x_1, x_2, x_3)\cdot e^{-i 2\pi \left(\frac{m_1}{a_1} x_1+\frac{m_2}{a_2} x_2\right)} |
|||
\end{align} |
|||
</math> |
|||
We can write ''g'' once again as: |
|||
:<math>g(x_1, x_2, x_3)=\sum_{m_1=-\infty}^\infty \sum_{m_2=-\infty}^\infty h^\mathrm{two}(m_1, m_2, x_3) \cdot e^{i 2\pi \frac{m_1}{a_1} x_1} \cdot e^{i 2\pi \frac{m_2} |
|||
{a_2} x_2}</math> |
|||
Finally applying the same for the third coordinate, we define: |
|||
: <math> |
|||
\begin{align} |
|||
h^\mathrm{three}(m_1, m_2, m_3) & := \frac{1}{a_3}\int_0^{a_3} h^\mathrm{two}(m_1, m_2, x_3)\cdot e^{-i 2\pi \frac{m_3}{a_3} x_3}\, dx_3 \\[12pt] |
|||
& = \frac{1}{a_3}\int_0^{a_3} dx_3 \frac{1}{a_2}\int_0^{a_2} dx_2 \frac{1}{a_1}\int_0^{a_1} dx_1 g(x_1, x_2, x_3)\cdot e^{-i 2\pi \left(\frac{m_1}{a_1} x_1+\frac{m_2}{a_2} x_2 + \frac{m_3}{a_3} x_3\right)} |
|||
\end{align} |
|||
</math> |
|||
We write ''g'' as: |
|||
:<math>g(x_1, x_2, x_3)=\sum_{m_1=-\infty}^\infty \sum_{m_2=-\infty}^\infty \sum_{m_3=-\infty}^\infty h^\mathrm{three}(m_1, m_2, m_3) \cdot e^{i 2\pi \frac{m_1}{a_1} x_1} \cdot e^{i 2\pi \frac{m_2}{a_2} x_2}\cdot e^{i 2\pi \frac{m_3}{a_3} x_3}</math> |
|||
Re-arranging: |
|||
:<math>g(x_1, x_2, x_3)=\sum_{m_1, m_2, m_3 \in \Z } h^\mathrm{three}(m_1, m_2, m_3) \cdot e^{i 2\pi \left( \frac{m_1}{a_1} x_1+ \frac{m_2}{a_2} x_2 + \frac{m_3}{a_3} x_3\right)}. </math> |
|||
Now, every ''reciprocal'' lattice vector can be written as <math>\mathbf{K} = l_{1}\mathbf{g}_{1} + l_{2}\mathbf{g}_{2} + l_{3}\mathbf{g}_{3}</math>, where ''l<sub>i</sub>'' are integers and '''g'''<sub>''i''</sub> are the reciprocal lattice vectors, we can use the fact that <math>\mathbf{g_i} \cdot \mathbf{a_j}=2\pi\delta_{ij}</math> to calculate that for any arbitrary reciprocal lattice vector '''K''' and arbitrary vector in space '''r''', their scalar product is: |
|||
:<math>\mathbf{K} \cdot \mathbf{r} = \left ( l_{1}\mathbf{g}_{1} + l_{2}\mathbf{g}_{2} + l_{3}\mathbf{g}_{3} \right ) \cdot \left (x_1\frac{\mathbf{a}_{1}}{a_1}+ x_2\frac{\mathbf{a}_{2}}{a_2} +x_3\frac{\mathbf{a}_{3}}{a_3} \right ) = 2\pi \left( x_1\frac{l_1}{a_1}+x_2\frac{l_2}{a_2}+x_3\frac{l_3}{a_3} \right ).</math> |
|||
And so it is clear that in our expansion, the sum is actually over reciprocal lattice vectors: |
|||
:<math>f(\mathbf{r})=\sum_{\mathbf{K}} h(\mathbf{K}) \cdot e^{i \mathbf{K} \cdot \mathbf{r}}, </math> |
|||
where |
|||
: <math>h(\mathbf{K}) = \frac{1}{a_3}\int_0^{a_3} dx_3 \frac{1}{a_2}\int_0^{a_2} dx_2 \frac{1}{a_1}\int_0^{a_1} dx_1 f\left(x_1\frac{\mathbf{a}_{1}}{a_1}+x_2\frac{\mathbf{a}_{2}}{a_2}+x_3\frac{\mathbf{a}_{3}}{a_3} \right)\cdot e^{-i \mathbf{K} \cdot \mathbf{r}}. </math> |
|||
Assuming |
|||
:<math>\mathbf{r} = (x,y,z) = x_1\frac{\mathbf{a}_{1}}{a_1}+x_2\frac{\mathbf{a}_{2}}{a_2}+x_3\frac{\mathbf{a}_{3}}{a_3},</math> |
|||
we can solve this system of three linear equations for ''x'', ''y'', and ''z'' in terms of ''x''<sub>1</sub>, ''x''<sub>2</sub> and ''x''<sub>3</sub> in order to calculate the volume element in the original cartesian coordinate system. Once we have ''x'', ''y'', and ''z'' in terms of ''x''<sub>1</sub>, ''x''<sub>2</sub> and ''x''<sub>3</sub>, we can calculate [[Jacobian matrix and determinant|Jacobian determinant]]: |
|||
:<math>\begin{bmatrix} |
|||
\dfrac{\partial x_1}{\partial x} & \dfrac{\partial x_1}{\partial y} & \dfrac{\partial x_1}{\partial z} \\[3pt] |
|||
\dfrac{\partial x_2}{\partial x} & \dfrac{\partial x_2}{\partial y} & \dfrac{\partial x_2}{\partial z} \\[3pt] |
|||
\dfrac{\partial x_3}{\partial x} & \dfrac{\partial x_3}{\partial y} & \dfrac{\partial x_3}{\partial z} |
|||
\end{bmatrix}</math> |
|||
which after some calculation and applying some non-trivial cross-product identities can be shown to be equal to: |
|||
: <math>\frac{a_1 a_2 a_3}{\mathbf{a_1}\cdot(\mathbf{a_2} \times \mathbf{a_3})}</math> |
|||
(it may be advantageous for the sake of simplifying calculations, to work in such a cartesian coordinate system, in which it just so happens that '''a'''<sub>1</sub> is parallel to the x axis, '''a'''<sub>2</sub> lies in the ''x''-''y'' plane, and '''a'''<sub>3</sub> has components of all three axes). The denominator is exactly the volume of the primitive unit cell which is enclosed by the three primitive-vectors '''a'''<sub>1</sub>, '''a'''<sub>2</sub> and '''a'''<sub>3</sub>. In particular, we now know that |
|||
:<math>dx_1 \, dx_2 \, dx_3 = \frac{a_1 a_2 a_3}{\mathbf{a_1}\cdot(\mathbf{a_2} \times \mathbf{a_3})} \cdot dx \, dy \, dz. </math> |
|||
We can write now ''h''('''K''') as an integral with the traditional coordinate system over the volume of the primitive cell, instead of with the ''x''<sub>1</sub>, ''x''<sub>2</sub> and ''x''<sub>3</sub> variables: |
|||
:<math>h(\mathbf{K}) = \frac{1}{\mathbf{a_1}\cdot(\mathbf{a_2} \times \mathbf{a_3})}\int_{C} d\mathbf{r} f(\mathbf{r})\cdot e^{-i \mathbf{K} \cdot \mathbf{r}} </math> |
|||
And ''C'' is the primitive unit cell, thus, <math>\mathbf{a_1}\cdot(\mathbf{a_2} \times \mathbf{a_3})</math> is the volume of the primitive unit cell. |
|||
=== Hilbert space interpretation === |
|||
{{main|Hilbert space}} |
|||
In the language of [[Hilbert space]]s, the set of functions {''e<sub>n</sub>'' = ''e<sup>inx</sup>''; ''n'' ∈ '''Z'''} is an [[orthonormal basis]] for the space ''L''<sup>2</sup>([−π, π]) of square-integrable functions of [−π, π]. This space is actually a Hilbert space with an [[inner product]] given for any two elements ''f'' and ''g'' by |
|||
:<math>\langle f,\, g \rangle \;\stackrel{\mathrm{def}}{=} \; \frac{1}{2\pi}\int_{-\pi}^{\pi} f(x)\overline{g(x)}\,dx.</math> |
|||
The basic Fourier series result for Hilbert spaces can be written as |
|||
:<math>f=\sum_{n=-\infty}^\infty \langle f,e_n \rangle \, e_n.</math> |
|||
[[File:Fourier series integral identities.gif|thumb|400px|right|Sines and cosines form an orthonormal set, as illustrated above. The integral of sine, cosine and their product is zero (green and red areas are equal, and cancel out) when ''m'', ''n'' or the functions are different, and pi only if ''m'' and ''n'' are equal, and the function used is the same.]] |
|||
This corresponds exactly to the complex exponential formulation given above. The version with sines and cosines is also justified with the Hilbert space interpretation. Indeed, the sines and cosines form an [[orthonormal set|orthogonal set]]: |
|||
:<math>\int_{-\pi}^{\pi} \cos(mx)\, \cos(nx)\, dx = \pi \delta_{mn}, \quad m, n \ge 1, \, </math> |
|||
:<math>\int_{-\pi}^{\pi} \sin(mx)\, \sin(nx)\, dx = \pi \delta_{mn}, \quad m, n \ge 1</math> |
|||
(where δ<sub>''mn''</sub> is the [[Kronecker delta]]), and |
|||
:<math>\int_{-\pi}^{\pi} \cos(mx)\, \sin(nx)\, dx = 0;\,</math> |
|||
furthermore, the sines and cosines are orthogonal to the constant function '''1'''. An ''orthonormal basis'' for ''L''<sup>2</sup>([−π, π]) consisting of real functions is formed by the functions 1/{{sqrt|2π}} '''1''' and 1/{{sqrt|π}} cos(''nx''),  1/{{sqrt|π}} sin(''nx'') with ''n'' = 1, 2,... The density of their span is a consequence of the [[Stone–Weierstrass theorem]], but follows also from the properties of classical kernels like the [[Fejér kernel]]. |
|||
== Properties == |
|||
We say that ''f'' belongs to <math>C^k(\mathbb{T})</math> if ''f'' is a 2π-periodic function on '''R''' which is ''k'' times differentiable, and its ''k''th derivative is continuous. |
|||
* If ''f'' is a 2π-periodic [[odd function]], then ''a<sub>n</sub>'' = 0 for all ''n''. |
|||
* If ''f'' is a 2π-periodic [[even function]], then ''b<sub>n</sub>'' = 0 for all ''n''. |
|||
* If ''f'' is [[integrable]], <math>\lim_{|n|\rightarrow \infty}\hat{f}(n)=0</math>, <math>\lim_{n\rightarrow +\infty}a_n=0</math> and <math>\lim_{n\rightarrow +\infty}b_n=0.</math> This result is known as the [[Riemann–Lebesgue lemma]]. |
|||
* A [[doubly infinite]] sequence {''a<sub>n</sub>''} in ''c''<sub>0</sub>('''Z''') is the sequence of Fourier coefficients of a function in ''L''<sup>1</sup>([0, 2π]) if and only if it is a convolution of two sequences in <math>\ell^2(\mathbf{Z})</math>. See [http://mathoverflow.net/questions/46626/characterizations-of-a-linear-subspace-associated-with-fourier-series] |
|||
* If <math>f \in C^1(\mathbb{T})</math>, then the Fourier coefficients <math>\widehat{f'}(n)</math> of the derivative ''f′'' can be expressed in terms of the Fourier coefficients <math>\hat{f}(n)</math> of the function ''f'', via the formula <math>\widehat{f'}(n) = in \hat{f}(n)</math>. |
|||
* If <math>f \in C^k(\mathbb{T})</math>, then <math>\widehat{f^{(k)}}(n) = (in)^k \hat{f}(n)</math>. In particular, since <math>\widehat{f^{(k)}}(n)</math> tends to zero, we have that <math>|n|^k\hat{f}(n)</math> tends to zero, which means that the Fourier coefficients converge to zero faster than the ''k''th power of ''n''. |
|||
* [[Parseval's theorem]]. If ''f'' belongs to ''L''<sup>2</sup>([−π, π]), then <math>\sum_{n=-\infty}^\infty |\hat{f}(n)|^2 = \frac{1}{2\pi}\int_{-\pi}^{\pi} |f(x)|^2 \, dx</math>. |
|||
* [[Plancherel's theorem]]. If <math>c_0,\, c_{\pm 1},\, c_{\pm 2},\ldots</math> are coefficients and <math>\sum_{n=-\infty}^\infty |c_n|^2 < \infty</math> then there is a unique function <math>f\in L^2([-\pi,\pi])</math> such that <math>\hat{f}(n) = c_n</math> for every ''n''. |
|||
* The first convolution theorem states that if ''f'' and ''g'' are in ''L''<sup>1</sup>([−π, π]), the Fourier series coefficients of the 2π-periodic [[convolution]] of ''f'' and ''g'' are given by: |
|||
::<math>[\widehat{f*_{2\pi}g}](n) = 2\pi\cdot \hat{f}(n)\cdot\hat{g}(n),</math><ref group="nb">The scale factor is always equal to the period, 2π in this case.<!-- You can easily verify that the factor is necessary here, by choosing f and g to be constant 1. --></ref> |
|||
:where: |
|||
::<math>\begin{align} |
|||
\left[f*_{2\pi}g\right](x) \ &\stackrel{\mathrm{def}}{=} \int_{-\pi}^{\pi} f(u)\cdot g[\text{pv}(x-u)] du, && |
|||
\big(\text{and }\underbrace{\text{pv}(x) \ \stackrel{\mathrm{def}}{=} \text{Arg}\left(e^{ix}\right) |
|||
}_{\text{principal value}}\big)\\ |
|||
&= \int_{-\pi}^{\pi} f(u)\cdot g(x-u)\, du, &&\scriptstyle \text{when g(x) is 2}\pi\text{-periodic.}\\ |
|||
&= \int_{2\pi} f(u)\cdot g(x-u)\, du, &&\scriptstyle \text{when both functions are 2}\pi\text{-periodic, and the integral is over any 2}\pi\text{ interval.} |
|||
\end{align}</math> |
|||
* The second convolution theorem states that the Fourier series coefficients of the product of ''f'' and ''g'' are given by the [[Convolution#Discrete convolution|discrete convolution]] of the <math>\hat f</math> and <math>\hat g</math> sequences: |
|||
::<math>[\widehat{f\cdot g}](n) = [\hat{f}*\hat{g}](n).</math> |
|||
=== Compact groups === |
|||
{{main|Compact group|Lie group|Peter–Weyl theorem}} |
|||
One of the interesting properties of the Fourier transform which we have mentioned, is that it carries convolutions to pointwise products. If that is the property which we seek to preserve, one can produce Fourier series on any [[compact group]]. Typical examples include those [[classical group]]s that are compact. This generalizes the Fourier transform to all spaces of the form ''L''<sup>2</sup>(''G''), where ''G'' is a compact group, in such a way that the Fourier transform carries [[convolution]]s to pointwise products. The Fourier series exists and converges in similar ways to the [−π, π] case. |
|||
An alternative extension to compact groups is the [[Peter–Weyl theorem]], which proves results about representations of compact groups analogous to those about finite groups. |
|||
=== Riemannian manifolds === |
|||
[[File:AtomicOrbital n4 l2.png|thumb|right|The [[atomic orbital]]s of [[chemistry]] are [[spherical harmonic]]s and can be used to produce Fourier series on the [[sphere]].]] |
|||
{{main|Laplace operator|Riemannian manifold}} |
|||
If the domain is not a group, then there is no intrinsically defined convolution. However, if ''X'' is a [[Compact space|compact]] [[Riemannian manifold]], it has a [[Laplace–Beltrami operator]]. The Laplace–Beltrami operator is the differential operator that corresponds to [[Laplace operator]] for the Riemannian manifold ''X''. Then, by analogy, one can consider heat equations on ''X''. Since Fourier arrived at his basis by attempting to solve the heat equation, the natural generalization is to use the eigensolutions of the Laplace–Beltrami operator as a basis. This generalizes Fourier series to spaces of the type ''L''<sup>2</sup>(''X''), where ''X'' is a Riemannian manifold. The Fourier series converges in ways similar to the [−π, π] case. A typical example is to take ''X'' to be the sphere with the usual metric, in which case the Fourier basis consists of [[spherical harmonics]]. |
|||
=== Locally compact Abelian groups === |
|||
{{main|Pontryagin duality}} |
|||
The generalization to compact groups discussed above does not generalize to noncompact, nonabelian groups. However, there is a straightfoward generalization to Locally Compact Abelian (LCA) groups. |
|||
This generalizes the Fourier transform to ''L''<sup>1</sup>(''G'') or ''L''<sup>2</sup>(''G''), where ''G'' is an LCA group. If ''G'' is compact, one also obtains a Fourier series, which converges similarly to the [−π, π] case, but if ''G'' is noncompact, one obtains instead a [[Fourier integral]]. This generalization yields the usual [[Fourier transform]] when the underlying locally compact Abelian group is '''R'''. |
|||
==Approximation and convergence of Fourier series== |
|||
An important question for the theory as well as applications is that of convergence. In particular, it is often necessary in applications to replace the infinite series <math>\sum_{-\infty}^\infty</math>  by a finite one, |
|||
:<math>f_N(x) = \sum_{n=-N}^N \hat{f}(n) e^{inx}.</math> |
|||
This is called a ''partial sum''. We would like to know, in which sense does ''f''<sub>''N''</sub>(''x'') converge to ''f''(''x'') as ''N'' → ∞. |
|||
===Least squares property=== |
|||
We say that ''p'' is a [[trigonometric polynomial]] of degree ''N'' when it is of the form |
|||
:<math>p(x)=\sum_{n=-N}^N p_n e^{inx}.</math> |
|||
Note that ''f<sub>N</sub> is a trigonometric polynomial of degree ''N''. [[Parseval's theorem]] implies that |
|||
<blockquote>'''Theorem.''' The trigonometric polynomial ''f<sub>N</sub> is the unique best trigonometric polynomial of degree ''N'' approximating ''f''(''x''), in the sense that, for any trigonometric polynomial ''p'' ≠ ''f<sub>N</sub> of degree ''N'', we have |
|||
:<math>\|f_N - f\|_2 < \|p - f\|_2,</math> |
|||
where the Hilbert space norm is defined as: |
|||
:<math>\| g \|_2 = \sqrt{{1 \over 2\pi} \int_{-\pi}^{\pi} |g(x)|^2 \, dx}.</math> |
|||
</blockquote> |
|||
===Convergence=== |
|||
{{main|Convergence of Fourier series}} |
|||
{{See also|Gibbs phenomenon}} |
|||
Because of the least squares property, and because of the completeness of the Fourier basis, we obtain an elementary convergence result. |
|||
'''Theorem.''' If ''f'' belongs to ''L''<sup>2</sup>([−π, π]), then f<sub>∞</sub> converges to ''f'' in ''L''<sup>2</sup>([−π, π]), that is,  <math>\|f_N - f\|_2</math> converges to 0 as ''N'' → ∞. |
|||
We have already mentioned that if ''f'' is continuously differentiable, then <math>(i\cdot n) \hat{f}(n)</math> is the ''n''th Fourier coefficient of the derivative ''f''′. It follows, essentially from the [[Cauchy–Schwarz inequality]], that f<sub>∞</sub> is absolutely summable. The sum of this series is a continuous function, equal to ''f'', since the Fourier series converges in the mean to ''f'': |
|||
'''Theorem.''' If <math>f \in C^1(\mathbb{T})</math>, then f<sub>∞</sub> converges to ''f'' [[uniform convergence|uniformly]] (and hence also [[pointwise convergence|pointwise]].) |
|||
This result can be proven easily if ''f'' is further assumed to be ''C''<sup>2</sup>, since in that case <math>n^2\hat{f}(n)</math> tends to zero as ''n'' → ∞. More generally, the Fourier series is absolutely summable, thus converges uniformly to ''f'', provided that ''f'' satisfies a [[Hölder condition]] of order α > ½. In the absolutely summable case, the inequality <math>\sup_x |f(x) - f_N(x)| \le \sum_{|n| > N} |\hat{f}(n)|</math>  proves uniform convergence. |
|||
Many other results concerning the [[convergence of Fourier series]] are known, ranging from the moderately simple result that the series converges at ''x'' if ''f'' is differentiable at ''x'', to [[Lennart Carleson]]'s much more sophisticated result that the Fourier series of an ''L''<sup>2</sup> function actually converges [[almost everywhere]]. |
|||
These theorems, and informal variations of them that don't specify the convergence conditions, are sometimes referred to generically as "Fourier's theorem" or "the Fourier theorem".<ref>{{cite book |
|||
| title = Circuits, signals, and systems |
|||
| author = William McC. Siebert |
|||
| publisher = MIT Press |
|||
| year = 1985 |
|||
| isbn = 978-0-262-19229-3 |
|||
| page = 402 |
|||
| url = http://books.google.com/?id=zBTUiIrb2WIC&pg=PA402&dq=%22fourier%27s+theorem%22 |
|||
}}</ref><ref>{{cite book |
|||
| title = Advances in Electronics and Electron Physics |
|||
| author = L. Marton and Claire Marton |
|||
| publisher = Academic Press |
|||
| year = 1990 |
|||
| isbn = 978-0-12-014650-5 |
|||
| page = 369 |
|||
| url = http://books.google.com/?id=27c1WOjCBX4C&pg=PA369&dq=%22fourier+theorem%22 |
|||
}}</ref><ref>{{cite book |
|||
| title = Solid-state spectroscopy |
|||
| author = Hans Kuzmany |
|||
| publisher = Springer |
|||
| year = 1998 |
|||
| isbn = 978-3-540-63913-8 |
|||
| page = 14 |
|||
| url = http://books.google.com/?id=-laOoZitZS8C&pg=PA14&dq=%22fourier+theorem%22 |
|||
}}</ref><ref>{{cite book |
|||
| title = Brain and perception |
|||
| author = Karl H. Pribram, Kunio Yasue, and Mari Jibu |
|||
| publisher = Lawrence Erlbaum Associates |
|||
| year = 1991 |
|||
| isbn = 978-0-89859-995-4 |
|||
| page = 26 |
|||
| url = http://books.google.com/?id=nsD4L2zsK4kC&pg=PA26&dq=%22fourier+theorem%22 |
|||
}}</ref> |
|||
=== Divergence === |
|||
Since Fourier series have such good convergence properties, many are often surprised by some of the negative results. For example, the Fourier series of a continuous ''T''-periodic function need not converge pointwise. The [[uniform boundedness principle]] yields a simple non-constructive proof of this fact. |
|||
In 1922, [[Andrey Kolmogorov]] published an article entitled "[http://translate.google.com/#fr/en/Une%20s%C3%A9rie%20de%20Fourier-Lebesgue%20divergente%20presque%20partout Une série de Fourier-Lebesgue divergente presque partout]" in which he gave an example of a Lebesgue-integrable function whose Fourier series diverges almost everywhere. He later constructed an example of an integrable function whose Fourier series diverges everywhere {{harv|Katznelson|1976}}. |
|||
==See also== |
|||
* [[ATS theorem]] |
|||
* [[Dirichlet kernel]] |
|||
* [[Discrete Fourier transform]] |
|||
* [[Fast Fourier transform]] |
|||
* [[Fejér's theorem]] |
|||
* [[Fourier sine and cosine series]] |
|||
* [[Gibbs phenomenon]] |
|||
* [[Laurent series]] — the substitution ''q'' = ''e''<sup>''ix''</sup> transforms a Fourier series into a Laurent series, or conversely. This is used in the ''q''-series expansion of the [[j-invariant|''j''-invariant]]. |
|||
* [[Multidimensional transform]] |
|||
* [[Spectral theory]] |
|||
* [[Sturm–Liouville theory]] |
|||
== Notes == |
|||
<references group="nb" /> |
|||
==References== |
|||
{{Reflist|2}} |
|||
===Further reading=== |
|||
* {{cite book |author=William E. Boyce and Richard C. DiPrima |title=Elementary Differential Equations and Boundary Value Problems |edition=8th |publisher=John Wiley & Sons, Inc. |location=New Jersey |year=2005 |isbn=0-471-43338-1}} |
|||
* {{cite book | author = Joseph Fourier, translated by Alexander Freeman | title = The Analytical Theory of Heat | publisher = Dover Publications | year = published 1822, translated 1878, re-released 2003 | isbn = 0-486-49531-0 }} 2003 unabridged republication of the 1878 English translation by Alexander Freeman of Fourier's work ''Théorie Analytique de la Chaleur'', originally published in 1822. |
|||
* {{cite journal |author=Enrique A. Gonzalez-Velasco |title=Connections in Mathematical Analysis: The Case of Fourier Series |journal=American Mathematical Monthly |volume=99 |year=1992 |pages=427–441 |issue=5 |doi=10.2307/2325087}} |
|||
* {{Cite journal| last=Katznelson| first= Yitzhak| title=An introduction to harmonic analysis| edition = Second corrected | publisher = Dover Publications, Inc | year=1976 | location=New York | ref=harv | isbn=0-486-63331-4}} |
|||
* [[Felix Klein]], ''Development of mathematics in the 19th century''. Mathsci Press Brookline, Mass, 1979. Translated by M. Ackerman from ''Vorlesungen über die Entwicklung der Mathematik im 19 Jahrhundert'', Springer, Berlin, 1928. |
|||
* {{cite book |author=Walter Rudin |title=Principles of mathematical analysis |edition=3rd |publisher=McGraw-Hill, Inc. |location=New York |year=1976 |isbn=0-07-054235-X}} |
|||
* {{cite book | author=A. Zygmund | title=Trigonometric series | edition=third | publisher = Cambridge University Press | location=Cambridge | year=2002 | isbn=0-521-89053-5}} The first edition was published in 1935. |
|||
==External links== |
|||
* [http://www.thefouriertransform.com/series/fourier.php thefouriertransform.com] Fourier Series as a prelude to the Fourier Transform |
|||
* [http://mathoverflow.net/questions/46626/characterizations-of-a-linear-subspace-associated-with-fourier-series]-Characterizations of a linear subspace associated with Fourier series |
|||
* [http://www.fourier-series.com/fourierseries2/fourier_series_tutorial.html An interactive flash tutorial for the Fourier Series] |
|||
* [http://www.jhu.edu/~signals/phasorapplet2/phasorappletindex.htm Phasor Phactory] Allows custom control of the harmonic amplitudes for arbitrary terms |
|||
* [http://www.falstad.com/fourier/ Java applet] shows Fourier series expansion of an arbitrary function |
|||
* [http://www.exampleproblems.com/wiki/index.php/Fourier_Series Example problems] — Examples of computing Fourier Series |
|||
*{{springer|title=Fourier series|id=p/f041090}} |
|||
* {{MathWorld | urlname= FourierSeries | title= Fourier Series}} |
|||
* [http://math.fullerton.edu/mathews/c2003/FourierSeriesComplexMod.html Fourier Series Module by John H. Mathews] |
|||
* [http://www.shsu.edu/~icc_cmf/bio/fourier.html Joseph Fourier] — A site on Fourier's life which was used for the historical section of this article |
|||
* [http://www.sfu.ca/sonic-studio/handbook/Fourier_Theorem.html SFU.ca] — 'Fourier Theorem' |
|||
{{PlanetMath attribution|id=4718|title=example of Fourier series}} |
|||
{{DEFAULTSORT:Fourier Series}} |
|||
[[Category:Fourier series| ]] |
|||
[[Category:Joseph Fourier]] |
|||
Revision as of 19:52, 6 March 2014
| Fourier transforms |
|---|

In mathematics, a Fourier series (English: /ˈfɔːrieɪ/) decomposes periodic functions or periodic signals into the sum of a (possibly infinite) set of simple oscillating functions, namely sines and cosines (or complex exponentials). The study of Fourier series is a branch of Fourier analysis.
History
The Fourier series is named in honour of Jean-Baptiste Joseph Fourier (1768–1830), who made important contributions to the study of trigonometric series, after preliminary investigations by Leonhard Euler, Jean le Rond d'Alembert, and Daniel Bernoulli.[nb 1] Fourier introduced the series for the purpose of solving the heat equation in a metal plate, publishing his initial results in his 1807 Mémoire sur la propagation de la chaleur dans les corps solides (Treatise on the propagation of heat in solid bodies), and publishing his Théorie analytique de la chaleur in 1822. Early ideas of decomposing a periodic function into the sum of simple oscillating functions date back to the 3rd century BC, when ancient astronomers proposed an empiric model of planetary motions, based on deferents and epicycles.
The heat equation is a partial differential equation. Prior to Fourier's work, no solution to the heat equation was known in the general case, although particular solutions were known if the heat source behaved in a simple way, in particular, if the heat source was a sine or cosine wave. These simple solutions are now sometimes called eigensolutions. Fourier's idea was to model a complicated heat source as a superposition (or linear combination) of simple sine and cosine waves, and to write the solution as a superposition of the corresponding eigensolutions. This superposition or linear combination is called the Fourier series.
From a modern point of view, Fourier's results are somewhat informal, due to the lack of a precise notion of function and integral in the early nineteenth century. Later, Peter Gustav Lejeune Dirichlet[1] and Bernhard Riemann[2][3][4] expressed Fourier's results with greater precision and formality.
Although the original motivation was to solve the heat equation, it later became obvious that the same techniques could be applied to a wide array of mathematical and physical problems, and especially those involving linear differential equations with constant coefficients, for which the eigensolutions are sinusoids. The Fourier series has many such applications in electrical engineering, vibration analysis, acoustics, optics, signal processing, image processing, quantum mechanics, econometrics,[5] thin-walled shell theory,[6] etc.
Definition
In this section, s(x) denotes a function of the real variable x, and s is integrable on an interval [x0, x0 + P], for real numbers x0 and P. We will attempt to represent s in that interval as an infinite sum, or series, of harmonically related sinusoidal functions. Outside the interval, the series is periodic with period P (frequency 1/P). It follows that if s also has that property, the approximation is valid on the entire real line. We can begin with a finite summation (or partial sum):
is a periodic function with period P. Using the identities:
we can also write the function in these equivalent forms:
where:
When the coefficients (known as Fourier coefficients) are computed as follows:[7]
approximates on and the approximation improves as N → ∞. The infinite sum, is called the Fourier series representation of In engineering applications, the Fourier series is generally presumed to converge everywhere except at discontinuities, since the functions encountered in engineering are more well behaved than the ones that mathematicians can provide as counter-examples to this presumption. In particular, the Fourier series converges absolutely and uniformly to s(x) whenever the derivative of s(x) (which may not exist everywhere) is square integrable.[8] If a function is square-integrable on the interval [x0, x0+P], then the Fourier series converges to the function at almost every point. See Convergence of Fourier series. It is possible to define Fourier coefficients for more general functions or distributions, in such cases convergence in norm or weak convergence is usually of interest.
Example 1: a simple Fourier series

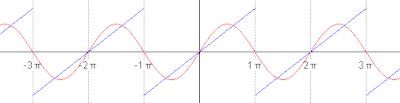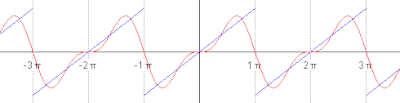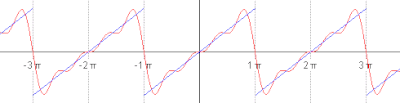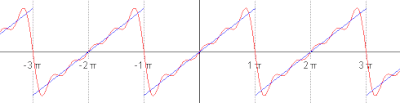
We now use the formula above to give a Fourier series expansion of a very simple function. Consider a sawtooth wave
In this case, the Fourier coefficients are given by
It can be proven that the Fourier series converges to s(x) at every point x where s is differentiable, and therefore:
| (Eq.1) |
When x = π, the Fourier series converges to 0, which is the half-sum of the left- and right-limit of s at x = π. This is a particular instance of the Dirichlet theorem for Fourier series.

Example 2: Fourier's motivation
The Fourier series expansion of our function in example 1 looks much less simple than the formula s(x) = x/π, and so it is not immediately apparent why one would need this Fourier series. While there are many applications, we cite Fourier's motivation of solving the heat equation. For example, consider a metal plate in the shape of a square whose side measures π meters, with coordinates (x, y) ∈ [0, π] × [0, π]. If there is no heat source within the plate, and if three of the four sides are held at 0 degrees Celsius, while the fourth side, given by y = π, is maintained at the temperature gradient T(x, π) = x degrees Celsius, for x in (0, π), then one can show that the stationary heat distribution (or the heat distribution after a long period of time has elapsed) is given by
Here, sinh is the hyperbolic sine function. This solution of the heat equation is obtained by multiplying each term of Eq.1 by sinh(ny)/sinh(nπ). While our example function s(x) seems to have a needlessly complicated Fourier series, the heat distribution T(x, y) is nontrivial. The function T cannot be written as a closed-form expression. This method of solving the heat problem was made possible by Fourier's work.
Other applications
Another application of this Fourier series is to solve the Basel problem by using Parseval's theorem. The example generalizes and one may compute ζ(2n), for any positive integer n.
Other common notations
The notation cn is inadequate for discussing the Fourier coefficients of several different functions. Therefore it is customarily replaced by a modified form of the function (s, in this case), such as or S, and functional notation often replaces subscripting:
In engineering, particularly when the variable x represents time, the coefficient sequence is called a frequency domain representation. Square brackets are often used to emphasize that the domain of this function is a discrete set of frequencies.
Another commonly used frequency domain representation uses the Fourier series coefficients to modulate a Dirac comb:
where f represents a continuous frequency domain. When variable x has units of seconds, f has units of hertz. The "teeth" of the comb are spaced at multiples (i.e. harmonics) of 1/P, which is called the fundamental frequency. can be recovered from this representation by an inverse Fourier transform:
The constructed function S(f) is therefore commonly referred to as a Fourier transform, even though the Fourier integral of a periodic function is not convergent at the harmonic frequencies.[nb 2]
Beginnings
Multiplying both sides by , and then integrating from to yields:
This immediately gives any coefficient ak of the trigonometrical series for φ(y) for any function which has such an expansion. It works because if φ has such an expansion, then (under suitable convergence assumptions) the integral
can be carried out term-by-term. But all terms involving for j ≠ k vanish when integrated from −1 to 1, leaving only the kth term.
In these few lines, which are close to the modern formalism used in Fourier series, Fourier revolutionized both mathematics and physics. Although similar trigonometric series were previously used by Euler, d'Alembert, Daniel Bernoulli and Gauss, Fourier believed that such trigonometric series could represent any arbitrary function. In what sense that is actually true is a somewhat subtle issue and the attempts over many years to clarify this idea have led to important discoveries in the theories of convergence, function spaces, and harmonic analysis.
When Fourier submitted a later competition essay in 1811, the committee (which included Lagrange, Laplace, Malus and Legendre, among others) concluded: ...the manner in which the author arrives at these equations is not exempt of difficulties and...his analysis to integrate them still leaves something to be desired on the score of generality and even rigour.[citation needed]
Birth of harmonic analysis
Since Fourier's time, many different approaches to defining and understanding the concept of Fourier series have been discovered, all of which are consistent with one another, but each of which emphasizes different aspects of the topic. Some of the more powerful and elegant approaches are based on mathematical ideas and tools that were not available at the time Fourier completed his original work. Fourier originally defined the Fourier series for real-valued functions of real arguments, and using the sine and cosine functions as the basis set for the decomposition.
Many other Fourier-related transforms have since been defined, extending the initial idea to other applications. This general area of inquiry is now sometimes called harmonic analysis. A Fourier series, however, can be used only for periodic functions, or for functions on a bounded (compact) interval.
Extensions
Fourier series on a square
We can also define the Fourier series for functions of two variables x and y in the square [−π, π]×[−π, π]:
Aside from being useful for solving partial differential equations such as the heat equation, one notable application of Fourier series on the square is in image compression. In particular, the jpeg image compression standard uses the two-dimensional discrete cosine transform, which is a Fourier transform using the cosine basis functions.
Fourier series of Bravais-lattice-periodic-function
The Bravais lattice is defined as the set of vectors of the form:
where ni are integers and ai are three linearly independent vectors. Assuming we have some function, f(r), such that it obeys the following condition for any Bravais lattice vector R: f(r) = f(r + R), we could make a Fourier series of it. This kind of function can be, for example, the effective potential that one electron "feels" inside a periodic crystal. It is useful to make a Fourier series of the potential then when applying Bloch's theorem. First, we may write any arbitrary vector r in the coordinate-system of the lattice:
where ai = |ai|.
Thus we can define a new function,
This new function, , is now a function of three-variables, each of which has periodicity a1, a2, a3 respectively: . If we write a series for g on the interval [0, a1] for x1, we can define the following:
And then we can write:
Further defining:
We can write g once again as:
Finally applying the same for the third coordinate, we define:
We write g as:
Re-arranging:
Now, every reciprocal lattice vector can be written as , where li are integers and gi are the reciprocal lattice vectors, we can use the fact that to calculate that for any arbitrary reciprocal lattice vector K and arbitrary vector in space r, their scalar product is:
And so it is clear that in our expansion, the sum is actually over reciprocal lattice vectors:
where
Assuming
we can solve this system of three linear equations for x, y, and z in terms of x1, x2 and x3 in order to calculate the volume element in the original cartesian coordinate system. Once we have x, y, and z in terms of x1, x2 and x3, we can calculate Jacobian determinant:
which after some calculation and applying some non-trivial cross-product identities can be shown to be equal to:
(it may be advantageous for the sake of simplifying calculations, to work in such a cartesian coordinate system, in which it just so happens that a1 is parallel to the x axis, a2 lies in the x-y plane, and a3 has components of all three axes). The denominator is exactly the volume of the primitive unit cell which is enclosed by the three primitive-vectors a1, a2 and a3. In particular, we now know that
We can write now h(K) as an integral with the traditional coordinate system over the volume of the primitive cell, instead of with the x1, x2 and x3 variables:
And C is the primitive unit cell, thus, is the volume of the primitive unit cell.
Hilbert space interpretation
In the language of Hilbert spaces, the set of functions {en = einx; n ∈ Z} is an orthonormal basis for the space L2([−π, π]) of square-integrable functions of [−π, π]. This space is actually a Hilbert space with an inner product given for any two elements f and g by
The basic Fourier series result for Hilbert spaces can be written as

This corresponds exactly to the complex exponential formulation given above. The version with sines and cosines is also justified with the Hilbert space interpretation. Indeed, the sines and cosines form an orthogonal set:
(where δmn is the Kronecker delta), and
furthermore, the sines and cosines are orthogonal to the constant function 1. An orthonormal basis for L2([−π, π]) consisting of real functions is formed by the functions 1/√2π 1 and 1/√π cos(nx), 1/√π sin(nx) with n = 1, 2,... The density of their span is a consequence of the Stone–Weierstrass theorem, but follows also from the properties of classical kernels like the Fejér kernel.
Properties
We say that f belongs to if f is a 2π-periodic function on R which is k times differentiable, and its kth derivative is continuous.
- If f is a 2π-periodic odd function, then an = 0 for all n.
- If f is a 2π-periodic even function, then bn = 0 for all n.
- If f is integrable, , and This result is known as the Riemann–Lebesgue lemma.
- A doubly infinite sequence {an} in c0(Z) is the sequence of Fourier coefficients of a function in L1([0, 2π]) if and only if it is a convolution of two sequences in . See [1]
- If , then the Fourier coefficients of the derivative f′ can be expressed in terms of the Fourier coefficients of the function f, via the formula .
- If , then . In particular, since tends to zero, we have that tends to zero, which means that the Fourier coefficients converge to zero faster than the kth power of n.
- Parseval's theorem. If f belongs to L2([−π, π]), then .
- Plancherel's theorem. If are coefficients and then there is a unique function such that for every n.
- The first convolution theorem states that if f and g are in L1([−π, π]), the Fourier series coefficients of the 2π-periodic convolution of f and g are given by:
- where:
- The second convolution theorem states that the Fourier series coefficients of the product of f and g are given by the discrete convolution of the and sequences:
Compact groups
One of the interesting properties of the Fourier transform which we have mentioned, is that it carries convolutions to pointwise products. If that is the property which we seek to preserve, one can produce Fourier series on any compact group. Typical examples include those classical groups that are compact. This generalizes the Fourier transform to all spaces of the form L2(G), where G is a compact group, in such a way that the Fourier transform carries convolutions to pointwise products. The Fourier series exists and converges in similar ways to the [−π, π] case.
An alternative extension to compact groups is the Peter–Weyl theorem, which proves results about representations of compact groups analogous to those about finite groups.
Riemannian manifolds

If the domain is not a group, then there is no intrinsically defined convolution. However, if X is a compact Riemannian manifold, it has a Laplace–Beltrami operator. The Laplace–Beltrami operator is the differential operator that corresponds to Laplace operator for the Riemannian manifold X. Then, by analogy, one can consider heat equations on X. Since Fourier arrived at his basis by attempting to solve the heat equation, the natural generalization is to use the eigensolutions of the Laplace–Beltrami operator as a basis. This generalizes Fourier series to spaces of the type L2(X), where X is a Riemannian manifold. The Fourier series converges in ways similar to the [−π, π] case. A typical example is to take X to be the sphere with the usual metric, in which case the Fourier basis consists of spherical harmonics.
Locally compact Abelian groups
The generalization to compact groups discussed above does not generalize to noncompact, nonabelian groups. However, there is a straightfoward generalization to Locally Compact Abelian (LCA) groups.
This generalizes the Fourier transform to L1(G) or L2(G), where G is an LCA group. If G is compact, one also obtains a Fourier series, which converges similarly to the [−π, π] case, but if G is noncompact, one obtains instead a Fourier integral. This generalization yields the usual Fourier transform when the underlying locally compact Abelian group is R.
Approximation and convergence of Fourier series
An important question for the theory as well as applications is that of convergence. In particular, it is often necessary in applications to replace the infinite series by a finite one,
This is called a partial sum. We would like to know, in which sense does fN(x) converge to f(x) as N → ∞.
Least squares property
We say that p is a trigonometric polynomial of degree N when it is of the form
Note that fN is a trigonometric polynomial of degree N. Parseval's theorem implies that
Theorem. The trigonometric polynomial fN is the unique best trigonometric polynomial of degree N approximating f(x), in the sense that, for any trigonometric polynomial p ≠ fN of degree N, we have
where the Hilbert space norm is defined as:
Convergence
Because of the least squares property, and because of the completeness of the Fourier basis, we obtain an elementary convergence result.
Theorem. If f belongs to L2([−π, π]), then f∞ converges to f in L2([−π, π]), that is, converges to 0 as N → ∞.
We have already mentioned that if f is continuously differentiable, then is the nth Fourier coefficient of the derivative f′. It follows, essentially from the Cauchy–Schwarz inequality, that f∞ is absolutely summable. The sum of this series is a continuous function, equal to f, since the Fourier series converges in the mean to f:
Theorem. If , then f∞ converges to f uniformly (and hence also pointwise.)
This result can be proven easily if f is further assumed to be C2, since in that case tends to zero as n → ∞. More generally, the Fourier series is absolutely summable, thus converges uniformly to f, provided that f satisfies a Hölder condition of order α > ½. In the absolutely summable case, the inequality proves uniform convergence.
Many other results concerning the convergence of Fourier series are known, ranging from the moderately simple result that the series converges at x if f is differentiable at x, to Lennart Carleson's much more sophisticated result that the Fourier series of an L2 function actually converges almost everywhere.
These theorems, and informal variations of them that don't specify the convergence conditions, are sometimes referred to generically as "Fourier's theorem" or "the Fourier theorem".[10][11][12][13]
Divergence
Since Fourier series have such good convergence properties, many are often surprised by some of the negative results. For example, the Fourier series of a continuous T-periodic function need not converge pointwise. The uniform boundedness principle yields a simple non-constructive proof of this fact.
In 1922, Andrey Kolmogorov published an article entitled "Une série de Fourier-Lebesgue divergente presque partout" in which he gave an example of a Lebesgue-integrable function whose Fourier series diverges almost everywhere. He later constructed an example of an integrable function whose Fourier series diverges everywhere (Katznelson 1976).
See also
- ATS theorem
- Dirichlet kernel
- Discrete Fourier transform
- Fast Fourier transform
- Fejér's theorem
- Fourier sine and cosine series
- Gibbs phenomenon
- Laurent series — the substitution q = eix transforms a Fourier series into a Laurent series, or conversely. This is used in the q-series expansion of the j-invariant.
- Multidimensional transform
- Spectral theory
- Sturm–Liouville theory
Notes
- ^ These three did some important early work on the wave equation, especially D'Alembert. Euler's work in this area was mostly comtemporaneous/ in collaboration with Bernoulli, although the latter made some independent contributions to the theory of waves and vibrations (see here, pg.s 209 & 210, ).
- ^ Since the integral defining the Fourier transform of a periodic function is not convergent, it is necessary to view the periodic function and its transform as distributions. In this sense is a Dirac delta function, which is an example of a distribution.
- ^ These words are not strictly Fourier's. Whilst the cited article does list the author as Fourier, a footnote indicates that the article was actually written by Poisson (that it was not written by Fourier is also clear from the consistent use of the third person to refer to him) and that it is, "for reasons of historical interest", presented as though it were Fourier's original memoire.
- ^ The scale factor is always equal to the period, 2π in this case.
References
- ^ Lejeune-Dirichlet, P. "Sur la convergence des séries trigonométriques qui servent à représenter une fonction arbitraire entre des limites données". (In French), transl. "On the convergence of trigonometric series which serve to represent an arbitrary function between two given limits". Journal f¨ur die reine und angewandte Mathematik, Vol. 4 (1829) p. 157–169.
- ^ "Ueber die Darstellbarkeit einer Function durch eine trigonometrische Reihe". Habilitationschrift, Göttingen; 1854. Abhandlungen der Königlichen Gesellschaft der Wissenschaften zu Göttingen, vol. 13, 1867. Published posthumously for Riemann by Richard Dedekind (in German). Archived from the original on 20 May 2008. Retrieved 19 May 2008.
{{cite web}}: Italic or bold markup not allowed in:|work=(help); Unknown parameter|deadurl=ignored (|url-status=suggested) (help); Unknown parameter|trans_title=ignored (|trans-title=suggested) (help) - ^ D. Mascre, Bernhard Riemann: Posthumous Thesis on the Representation of Functions by Triginometric Series (1867). Landmark Writings in Western Mathematics 1640–1940, Ivor Grattan-Guinness (ed.); pg. 492. Elsevier, 20 May 2005.Accessed 7 Dec 2012.</
- ^ Theory of Complex Functions: Readings in Mathematics, by Reinhold Remmert; pg 29. Springer, 1991. Accessed 7 Dec 2012.
- ^ Nerlove, Marc; Grether, David M.; Carvalho, Jose L. (1995). Analysis of Economic Time Series. Economic Theory, Econometrics, and Mathematical Economics. Elsevier. ISBN 0-12-515751-7.
- ^ Flugge, Wilhelm (1957). Statik und Dynamik der Schalen. Berlin: Springer-Verlag.
- ^ Dorf, Richard C.; Tallarida, Ronald J. (1993-07-15). Pocket Book of Electrical Engineering Formulas (1 ed.). Boca Raton,FL: CRC Press. pp. 171–174. ISBN 0849344735.
- ^ Georgi P. Tolstov (1976). Fourier Series. Courier-Dover. ISBN 0-486-63317-9.
- ^ Gallica - Fourier, Jean-Baptiste-Joseph (1768–1830). Oeuvres de Fourier. 1888, pp. 218–219,
- ^ William McC. Siebert (1985). Circuits, signals, and systems. MIT Press. p. 402. ISBN 978-0-262-19229-3.
- ^ L. Marton and Claire Marton (1990). Advances in Electronics and Electron Physics. Academic Press. p. 369. ISBN 978-0-12-014650-5.
- ^ Hans Kuzmany (1998). Solid-state spectroscopy. Springer. p. 14. ISBN 978-3-540-63913-8.
- ^ Karl H. Pribram, Kunio Yasue, and Mari Jibu (1991). Brain and perception. Lawrence Erlbaum Associates. p. 26. ISBN 978-0-89859-995-4.
{{cite book}}: CS1 maint: multiple names: authors list (link)
Further reading
- William E. Boyce and Richard C. DiPrima (2005). Elementary Differential Equations and Boundary Value Problems (8th ed.). New Jersey: John Wiley & Sons, Inc. ISBN 0-471-43338-1.
- Joseph Fourier, translated by Alexander Freeman (published 1822, translated 1878, re-released 2003). The Analytical Theory of Heat. Dover Publications. ISBN 0-486-49531-0.
{{cite book}}: Check date values in:|year=(help)CS1 maint: year (link) 2003 unabridged republication of the 1878 English translation by Alexander Freeman of Fourier's work Théorie Analytique de la Chaleur, originally published in 1822. - Enrique A. Gonzalez-Velasco (1992). "Connections in Mathematical Analysis: The Case of Fourier Series". American Mathematical Monthly. 99 (5): 427–441. doi:10.2307/2325087.
- Katznelson, Yitzhak (1976). "An introduction to harmonic analysis" (Second corrected ed.). New York: Dover Publications, Inc. ISBN 0-486-63331-4.
{{cite journal}}: Cite journal requires|journal=(help); Invalid|ref=harv(help) - Felix Klein, Development of mathematics in the 19th century. Mathsci Press Brookline, Mass, 1979. Translated by M. Ackerman from Vorlesungen über die Entwicklung der Mathematik im 19 Jahrhundert, Springer, Berlin, 1928.
- Walter Rudin (1976). Principles of mathematical analysis (3rd ed.). New York: McGraw-Hill, Inc. ISBN 0-07-054235-X.
- A. Zygmund (2002). Trigonometric series (third ed.). Cambridge: Cambridge University Press. ISBN 0-521-89053-5. The first edition was published in 1935.
External links
- thefouriertransform.com Fourier Series as a prelude to the Fourier Transform
- [2]-Characterizations of a linear subspace associated with Fourier series
- An interactive flash tutorial for the Fourier Series
- Phasor Phactory Allows custom control of the harmonic amplitudes for arbitrary terms
- Java applet shows Fourier series expansion of an arbitrary function
- Example problems — Examples of computing Fourier Series
- "Fourier series", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Weisstein, Eric W. "Fourier Series". MathWorld.
- Fourier Series Module by John H. Mathews
- Joseph Fourier — A site on Fourier's life which was used for the historical section of this article
- SFU.ca — 'Fourier Theorem'
This article incorporates material from example of Fourier series on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.











![{\displaystyle \scriptstyle [x_{0},\ x_{0}+P],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e15dd8a7d5176a8625325e2afb151fbdd825a142)





![{\displaystyle {\begin{aligned}s(x)&={\frac {a_{0}}{2}}+\sum _{n=1}^{\infty }\left[a_{n}\cos \left(nx\right)+b_{n}\sin \left(nx\right)\right]\\&={\frac {2}{\pi }}\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}\sin(nx),\quad \mathrm {for} \quad x-\pi \notin 2\pi \mathbf {Z} .\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e4f7723030e9a65dde2b59bdffde660c5ac6d1a4)


![{\displaystyle {\begin{aligned}s_{\infty }(x)&=\sum _{n=-\infty }^{\infty }{\hat {s}}(n)\cdot e^{i{\tfrac {2\pi nx}{P}}}\\&=\sum _{n=-\infty }^{\infty }S[n]\cdot e^{j{\tfrac {2\pi nx}{P}}}&&\scriptstyle {\text{common engineering notation}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1948743e8e50b99560a2e018c78b35e14e2111a1)
![{\displaystyle S(f)\ {\stackrel {\mathrm {def} }{=}}\ \sum _{n=-\infty }^{\infty }S[n]\cdot \delta \left(f-{\frac {n}{P}}\right),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/191fd9d4420479ce5300b692fbc43c0e5e703e89)

![{\displaystyle {\begin{aligned}{\mathcal {F}}^{-1}\{S(f)\}&=\int _{-\infty }^{\infty }\left(\sum _{n=-\infty }^{\infty }S[n]\cdot \delta \left(f-{\frac {n}{P}}\right)\right)e^{i2\pi fx}\,df,\\&=\sum _{n=-\infty }^{\infty }S[n]\cdot \int _{-\infty }^{\infty }\delta \left(f-{\frac {n}{P}}\right)e^{i2\pi fx}\,df,\\&=\sum _{n=-\infty }^{\infty }S[n]\cdot e^{i{\tfrac {2\pi nx}{P}}}\ \ {\stackrel {\mathrm {def} }{=}}\ s_{\infty }(x).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f87bc7f858006ce49e2b5c40d429076b92b96df)
















![{\displaystyle {\begin{aligned}h^{\mathrm {two} }(m_{1},m_{2},x_{3})&:={\frac {1}{a_{2}}}\int _{0}^{a_{2}}h^{\mathrm {one} }(m_{1},x_{2},x_{3})\cdot e^{-i2\pi {\frac {m_{2}}{a_{2}}}x_{2}}\,dx_{2}\\[12pt]&={\frac {1}{a_{2}}}\int _{0}^{a_{2}}dx_{2}{\frac {1}{a_{1}}}\int _{0}^{a_{1}}dx_{1}g(x_{1},x_{2},x_{3})\cdot e^{-i2\pi \left({\frac {m_{1}}{a_{1}}}x_{1}+{\frac {m_{2}}{a_{2}}}x_{2}\right)}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b375ad1bad97e4cee6cfa9c82d20582af5ba6b4)

![{\displaystyle {\begin{aligned}h^{\mathrm {three} }(m_{1},m_{2},m_{3})&:={\frac {1}{a_{3}}}\int _{0}^{a_{3}}h^{\mathrm {two} }(m_{1},m_{2},x_{3})\cdot e^{-i2\pi {\frac {m_{3}}{a_{3}}}x_{3}}\,dx_{3}\\[12pt]&={\frac {1}{a_{3}}}\int _{0}^{a_{3}}dx_{3}{\frac {1}{a_{2}}}\int _{0}^{a_{2}}dx_{2}{\frac {1}{a_{1}}}\int _{0}^{a_{1}}dx_{1}g(x_{1},x_{2},x_{3})\cdot e^{-i2\pi \left({\frac {m_{1}}{a_{1}}}x_{1}+{\frac {m_{2}}{a_{2}}}x_{2}+{\frac {m_{3}}{a_{3}}}x_{3}\right)}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bac3a4c30ff78f3abc70b6b65a6274b8899ca038)








![{\displaystyle {\begin{bmatrix}{\dfrac {\partial x_{1}}{\partial x}}&{\dfrac {\partial x_{1}}{\partial y}}&{\dfrac {\partial x_{1}}{\partial z}}\\[3pt]{\dfrac {\partial x_{2}}{\partial x}}&{\dfrac {\partial x_{2}}{\partial y}}&{\dfrac {\partial x_{2}}{\partial z}}\\[3pt]{\dfrac {\partial x_{3}}{\partial x}}&{\dfrac {\partial x_{3}}{\partial y}}&{\dfrac {\partial x_{3}}{\partial z}}\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5095a317a5c0975c5d1bdf27cd79d13b106a96a6)

























![{\displaystyle f\in L^{2}([-\pi ,\pi ])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/74d27747bf5e28fa54e94f218bd9296213ef25c5)

=2\pi \cdot {\hat {f}}(n)\cdot {\hat {g}}(n),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/956ea404aa998519c088c08c9a9e9f29c9bd38f0)
\ &{\stackrel {\mathrm {def} }{=}}\int _{-\pi }^{\pi }f(u)\cdot g[{\text{pv}}(x-u)]du,&&{\big (}{\text{and }}\underbrace {{\text{pv}}(x)\ {\stackrel {\mathrm {def} }{=}}{\text{Arg}}\left(e^{ix}\right)} _{\text{principal value}}{\big )}\\&=\int _{-\pi }^{\pi }f(u)\cdot g(x-u)\,du,&&\scriptstyle {\text{when g(x) is 2}}\pi {\text{-periodic.}}\\&=\int _{2\pi }f(u)\cdot g(x-u)\,du,&&\scriptstyle {\text{when both functions are 2}}\pi {\text{-periodic, and the integral is over any 2}}\pi {\text{ interval.}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1223be49e9c8285ec78e1a81ac52e7f983702eeb)


=[{\hat {f}}*{\hat {g}}](n).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a01ca431cbe51c2353a325265bb70204e5a1ae1)









