Faraday's law of induction: Difference between revisions
GliderMaven (talk | contribs) Revert to revision 598436290 dated 2014-03-06 18:59:19 by GliderMaven using popups |
Undid revision 598458707 by GliderMaven (talk)Please stop trying to impose your view in the consensus. |
||
| Line 1: | Line 1: | ||
#REDIRECT [[Electromagnetic induction#Faraday's law]] {{R from merge}} |
|||
{{R to section}} |
|||
{{For|the relationship between a time-varying magnetic field and an induced electric field|Maxwell's equations}} |
|||
{{electromagnetism|cTopic=Electrodynamics}} |
|||
'''Faraday's law of induction''' is a basic law of [[electromagnetism]] predicting how a [[magnetic field]] will interact with an [[electric circuit]] to produce an [[electromotive force|electromotive force (EMF)]]. It is the fundamental operating principle of [[transformer]]s, [[inductor]]s, and many types of [[electricity|electrical]] [[electric motor|motors]], [[electrical generator|generators]] and [[solenoid]]s.<ref name="Sadiku386">{{cite book|author=Sadiku, M. N. O.|title=Elements of Electromagnetics|year=2007|page=386|publisher=Oxford University Press|edition=fourth|location=New York (USA)/Oxford (UK)|url=http://books.google.com/?id=w2ITHQAACAAJ&dq=ISBN0-19-530048-3|isbn=0-19-530048-3}}</ref><ref>{{cite web|date=1999-07-22|title=Applications of electromagnetic induction|url=http://physics.bu.edu/~duffy/py106/Electricgenerators.html|publisher=[[Boston University]]}}</ref> |
|||
The '''Maxwell–Faraday equation''' is a generalisation of Faraday's law, and forms one of [[Maxwell's equations]]. |
|||
==History== |
|||
Faraday explained electromagnetic induction using a concept he called [[lines of force]]. However, scientists at the time widely rejected his theoretical ideas, mainly because they were not formulated mathematically.<ref name=Williams510>''Michael Faraday'', by L. Pearce Williams, p. 510</ref> An exception was [[James Clerk Maxwell|Maxwell]], who used Faraday's ideas as the basis of his quantitative electromagnetic theory.<ref name=Williams510/><ref>Maxwell, James Clerk (1904), ''A Treatise on Electricity and Magnetism'', Vol. II, Third Edition. Oxford University Press, pp. 178–9 and 189.</ref><ref name="IEEUK">[http://www.theiet.org/about/libarc/archives/biographies/faraday.cfm "Archives Biographies: Michael Faraday", The Institution of Engineering and Technology.]</ref> In Maxwell's papers, the time varying aspect of electromagnetic induction is expressed as a differential equation which [[Oliver Heaviside]] referred to as Faraday's law even though it is slightly different in form from the original version of Faraday's law, and does not describe [[#Faraday's law as two different phenomena|motional EMF]]. Heaviside's version (see [[#Maxwell–Faraday equation|Maxwell–Faraday equation below]]) is the form recognized today in the group of equations known as [[Maxwell's equations]]. |
|||
==Faraday's law== |
|||
===Qualitative statement=== |
|||
The most widespread version of Faraday's law states: |
|||
{{Quotation|The induced electromotive force in any closed circuit is equal to the negative of the time rate of change of the [[magnetic flux]] through the circuit.}} |
|||
This version of Faraday's law strictly holds only when the closed circuit is a loop of infinitely thin wire,<ref name=Feynman/> and is invalid in other circumstances as discussed [[#"Counterexamples" to Faraday's law|below]]. A different version, the [[Maxwell–Faraday equation]] (discussed [[#Maxwell–Faraday equation|below]]), is valid in all circumstances. |
|||
===Quantitative=== |
|||
[[Image:Surface integral illustration.png|right|thumb|The definition of surface integral relies on splitting the surface Σ into small surface elements. Each element is associated with a vector ''d'''''A''' of magnitude equal to the area of the element and with direction normal to the element and pointing “outward” (with respect to the orientation of the surface).]] |
|||
Faraday's law of induction makes use of the [[magnetic flux]] Φ<sub>''B''</sub> through a hypothetical surface Σ whose boundary is a wire loop. Since the wire loop may be moving, we write Σ(''t'') for the surface. The magnetic flux is defined by a [[surface integral]]: |
|||
::<math> \Phi_B = \iint\limits_{\Sigma(t)} \mathbf{B}(\mathbf{r}, t) \cdot d \mathbf{A}\ , </math> |
|||
where ''d'''''A''' is an element of surface area of the moving surface Σ(''t''), '''B''' is the magnetic field, and '''B'''·''d'''''A''' is a [[dot product|vector dot product]] (the infinitesimal amount of magnetic flux). In more visual terms, the magnetic flux through the wire loop is proportional to the number of [[field line|magnetic flux lines]] that pass through the loop. |
|||
When the flux changes—because '''B''' changes, or because the wire loop is moved or deformed, or both—Faraday's law of induction says that the wire loop acquires an [[electromotive force|EMF]], <math>\mathcal{E}</math>, defined as the energy available from a unit charge that has travelled once around the wire loop.<ref name=Feynman/><ref name=Griffiths2>{{cite book|author=Griffiths, David J.|title=Introduction to Electrodynamics|url=http://www.amazon.com/gp/reader/013805326X/ref=sib_dp_pt/104-2951702-6987112#reader-link|edition=Third|pages=301–303|publisher=Prentice Hall|year=1999|location=Upper Saddle River NJ|isbn=0-13-805326-X}}</ref><ref>Tipler and Mosca, ''Physics for Scientists and Engineers'', p795, [http://books.google.com/books?id=R2Nuh3Ux1AwC&pg=PA795 google books link]</ref><ref>Note that different textbooks may give different definitions. The set of equations used throughout the text was chosen to be compatible with the special relativity theory.</ref> Equivalently, it is the voltage that would be measured by cutting the wire to create an [[Electric circuit|open circuit]], and attaching a [[voltmeter]] to the leads. According to the [[Lorentz force law]] (in [[SI units]]), |
|||
:<math>\mathbf{F} = q \left(\mathbf{E} + \mathbf{v}\times\mathbf{B}\right) </math> |
|||
the EMF on a wire loop is: |
|||
:<math>\mathcal{E} = \frac{1}{q} \oint_{\mathrm{wire}}\mathbf{F}\cdot d\boldsymbol{\ell} = \oint_{\mathrm{wire}} \left(\mathbf{E} + \mathbf{v}\times\mathbf{B}\right)\cdot d\boldsymbol{\ell}</math> |
|||
where '''E''' is the [[electric field]], '''B''' is the [[magnetic field]] (aka magnetic flux density, magnetic induction), d'''ℓ''' is an infinitesimal [[arc length]] along the wire, and the [[line integral]] is evaluated along the wire (along the curve the conincident with the shape of the wire). |
|||
The EMF is also given by the [[time derivative|rate of change]] of the magnetic flux: |
|||
:<math>\mathcal{E} = -{{d\Phi_B} \over dt} \ </math>, |
|||
where <math>\mathcal{E}</math> is the [[electromotive force]] (EMF) in [[volt]]s and |
|||
Φ<sub>''B''</sub> is the [[magnetic flux]] in [[Weber (unit)|webers]]. The direction of the electromotive force is given by [[Lenz's law]]. |
|||
For a tightly wound [[inductor|coil of wire]], composed of ''N'' identical turns, each with the same Φ<sub>''B''</sub>, Faraday's law of induction states that<ref>Essential Principles of Physics, P.M. Whelan, M.J. Hodgeson, 2nd Edition, 1978, John Murray, ISBN 0-7195-3382-1</ref><ref>{{cite web|last=Nave|first=Carl R.|title=Faraday's Law|url=http://hyperphysics.phy-astr.gsu.edu/hbase/electric/farlaw.html|work=HyperPhysics|publisher=Georgia State University|accessdate=29 August 2011}}</ref> |
|||
:<math> \mathcal{E} = -N {{d\Phi_B} \over dt} </math> |
|||
where ''N'' is the number of turns of wire and Φ<sub>''B''</sub> is the magnetic flux in webers through a ''single'' loop. |
|||
===Maxwell–Faraday equation=== |
|||
[[Image:Stokes' Theorem.svg|thumb|right|An illustration of Kelvin-Stokes theorem with surface '''Σ''' its boundary '''∂Σ''' and orientation ''' ''n'' ''' set by the [[right-hand rule]].]] |
|||
The Maxwell–Faraday equation is a generalisation of Faraday's law that states that a time-varying magnetic field is always accompanied by a spatially-varying, non-[[Conservative vector field|conservative]] electric field, and vice-versa. The Maxwell–Faraday equation is |
|||
{{Equation box 1 |
|||
|indent =: |
|||
|equation = <math>\nabla \times \mathbf{E} = -\frac{\partial \mathbf{B}} {\partial t}</math> |
|||
|cellpadding |
|||
|border |
|||
|border colour = #50C878 |
|||
|background colour = #ECFCF4}} |
|||
(in [[SI units]]) where <math>\nabla\times</math> is the [[Curl (mathematics)|curl]] [[linear operator|operator]] and again '''E'''('''r''', ''t'') is the [[electric field]] and '''B'''('''r''', ''t'') is the [[magnetic field]]. These fields can generally be functions of position '''r''' and time ''t''. |
|||
The Maxwell–Faraday equation is one of the four [[Maxwell's equations]], and therefore plays a fundamental role in the theory of [[classical electromagnetism]]. It can also be written in an '''integral form''' by the [[Kelvin-Stokes theorem]]:<ref name=Harrington>{{cite book|author=Roger F Harrington|title=Introduction to electromagnetic engineering|year=2003|page=56|publisher=Dover Publications|location=Mineola, NY|isbn=0-486-43241-6|url=http://books.google.com/?id=ZlC2EV8zvX8C&pg=PA57&dq=%22faraday%27s+law+of+induction%22}}</ref> |
|||
{{Equation box 1 |
|||
|indent =: |
|||
|equation = <math> \oint_{\partial \Sigma} \mathbf{E} \cdot d\boldsymbol{\ell} = - \int_{\Sigma} \frac{\partial \mathbf{B}}{\partial t} \cdot d\mathbf{A} </math> |
|||
|cellpadding |
|||
|border |
|||
|border colour = #50C878 |
|||
|background colour = #ECFCF4}} |
|||
where, as indicated in the figure: |
|||
:'''Σ''' is a surface bounded by the closed contour '''∂Σ''', |
|||
:'''E''' is the electric field, '''B''' is the [[magnetic field]]. |
|||
:d'''ℓ''' is an [[infinitesimal]] vector element of the contour '''∂Σ''', |
|||
:d'''A''' is an infinitesimal vector element of surface '''Σ'''. If its direction is [[orthogonal]] to that surface patch, the magnitude is the area of an infinitesimal patch of surface. |
|||
Both d'''ℓ''' and d'''A''' have a sign ambiguity; to get the correct sign, the [[right-hand rule]] is used, as explained in the article [[Kelvin-Stokes theorem]]. For a planar surface Σ, a positive path element ''d'''''ℓ''' of curve ∂Σ is defined by the right-hand rule as one that points with the fingers of the right hand when the thumb points in the direction of the normal '''n''' to the surface Σ. |
|||
The integral around '''∂Σ''' is called a ''path integral'' or ''[[line integral]]''. |
|||
Notice that a nonzero [[Line integral|path integral]] for '''E''' is different from the behavior of the electric field generated by charges. A charge-generated '''E'''-field can be expressed as the gradient of a [[scalar field]] that is a solution to [[Poisson's equation]], and has a zero path integral. See [[gradient theorem]]. |
|||
The integral equation is true for ''any'' path '''∂Σ''' through space, and any surface '''Σ''' for which that path is a boundary. |
|||
If the path '''Σ''' is not changing in time, the equation can be rewritten: |
|||
:<math> \oint_{\partial \Sigma} \mathbf{E} \cdot d\boldsymbol{\ell} = - \frac{d}{dt} \int_{\Sigma} \mathbf{B} \cdot d\mathbf{A}. </math> |
|||
The [[surface integral]] at the right-hand side is the explicit expression for the [[magnetic flux]] Φ<sub>B</sub> through '''Σ'''. |
|||
==Proof of Faraday's law== |
|||
The four [[Maxwell's equations]] (including the Maxwell–Faraday equation), along with the [[Lorentz force law]], are a sufficient foundation to derive ''everything'' in [[classical electromagnetism]].<ref name=Feynman/><ref name=Griffiths2/> Therefore it is possible to "prove" Faraday's law starting with these equations.<ref name=Davison>{{cite doi|10.1119/1.1987339}}</ref><ref name=Krey>Basic Theoretical Physics: A Concise Overview by Krey and Owen, p155, [http://books.google.com/books?id=xZ_QelBmkxYC&pg=PA155 google books link]</ref> Click "show" in the box below for an outline of this proof. (In an alternative approach, not shown here but equally valid, Faraday's law could be taken as the starting point and used to "prove" the Maxwell–Faraday equation and/or other laws.) |
|||
:{| class="toccolours collapsible collapsed" width="80%" style="text-align:left" |
|||
!Outline of proof of Faraday's law from Maxwell's equations and the Lorentz force law. |
|||
|- |
|||
|Consider the time-derivative of flux through a possibly moving loop, with area <math>\Sigma(t)</math>: |
|||
:<math>\frac{d\Phi_B}{dt} = \frac{d}{dt}\int_{\Sigma(t)} \mathbf{B}(t)\cdot d\mathbf{A}</math> |
|||
The integral can change over time for two reasons: The integrand can change, or the integration region can change. These add linearly, therefore: |
|||
:<math>\left. \frac{d\Phi_B}{dt}\right|_{t=t_0} = \left( \int_{\Sigma(t_0)} \left. \frac{\partial\mathbf{B}}{\partial t}\right|_{t=t_0} \cdot d\mathbf{A}\right) + \left( \frac{d}{dt} \int_{\Sigma(t)} \mathbf{B}(t_0) \cdot d\mathbf{A} \right)</math> |
|||
where ''t''<sub>0</sub> is any given fixed time. We will show that the first term on the right-hand side corresponds to transformer EMF, the second to motional EMF (see above). The first term on the right-hand side can be rewritten using the integral form of the Maxwell–Faraday equation: |
|||
:<math> \int_{\Sigma(t_0)} \left. \frac{\partial \mathbf{B}}{\partial t}\right|_{t=t_0} \cdot d\mathbf{A} = - \oint_{\partial \Sigma(t_0)} \mathbf{E}(t_0) \cdot d\boldsymbol{\ell} </math> |
|||
[[Image:Faraday Area.PNG|thumbnail|300px|Area swept out by vector element ''d'''''ℓ''' of curve '''∂Σ''' in time ''dt'' when moving with velocity '''v'''.]] |
|||
Next, we analyze the second term on the right-hand side: |
|||
:<math>\frac{d}{dt} \int_{\Sigma(t)} \mathbf{B}(t_0) \cdot d\mathbf{A}</math> |
|||
This is the most difficult part of the proof; more details and alternate approaches can be found in references.<ref name=Davison/><ref name=Krey/><ref>K. Simonyi, Theoretische Elektrotechnik, 5th edition, VEB Deutscher Verlag der Wissenschaften, Berlin 1973, equation 20, page 47</ref> As the loop moves and/or deforms, it sweeps out a surface (see figure on right). The magnetic flux through this swept-out surface corresponds to the magnetic flux that is either entering or exiting the loop, and therefore this is the magnetic flux that contributes to the time-derivative. (This step implicitly uses [[Gauss's law for magnetism]]: Since the flux lines have no beginning or end, they can only get into the loop by getting cut through by the wire.) As a small part of the loop <math>d\boldsymbol{\ell}</math> moves with velocity '''v''' for a short time <math>dt</math>, it sweeps out a vector area vector <math>d\mathbf{A}=\mathbf{v} \, dt \times d\boldsymbol{\ell}</math>. Therefore, the change in magnetic flux through the loop here is |
|||
:<math>\mathbf{B} \cdot (\mathbf{v} \, dt \times d\boldsymbol{\ell}) = -dt \, d\boldsymbol{\ell} \cdot (\mathbf{v}\times\mathbf{B})</math> |
|||
Therefore: |
|||
:<math>\frac{d}{dt} \int_{\Sigma(t)} \mathbf{B}(t_0) \cdot d\mathbf{A} = -\oint_{\partial \Sigma(t_0)} (\mathbf{v}(t_0)\times \mathbf{B}(t_0))\cdot d\boldsymbol{\ell}</math> |
|||
where '''v''' is the velocity of a point on the loop <math>\partial \Sigma</math>. |
|||
Putting these together, |
|||
:<math>\left. \frac{d\Phi_B}{dt}\right|_{t=t_0} = \left(- \oint_{\partial \Sigma(t_0)} \mathbf{E}(t_0) \cdot d\boldsymbol{\ell}\right) + \left(- \oint_{\partial \Sigma(t_0)} (\mathbf{v}(t_0)\times \mathbf{B}(t_0))\cdot d\boldsymbol{\ell} \right)</math> |
|||
Meanwhile, EMF is defined as the energy available per unit charge that travels once around the wire loop. Therefore, by the [[Lorentz force law]], |
|||
:<math>EMF = \oint \left(\mathbf{E} + \mathbf{v}\times\mathbf{B}\right) \cdot \text{d}\boldsymbol{\ell}</math> |
|||
Combining these, |
|||
<math>\frac{d\Phi_B}{dt} = -EMF</math> |
|||
|} |
|||
=="Counterexamples" to Faraday's law== |
|||
<gallery widths="300px"> |
|||
Image:Faraday's disc.PNG|Faraday's disc electric generator. The disc rotates with angular rate ω, sweeping the conducting radius circularly in the static magnetic field '''B'''. The magnetic Lorentz force '''v <big>×</big> B''' drives the current along the conducting radius to the conducting rim, and from there the circuit completes through the lower brush and the axle supporting the disc. This device generates an EMF and a current, although the shape of the "circuit" is constant and thus the flux through the circuit does not change with time. |
|||
Image:FaradaysLawWithPlates.gif|A counterexample to Faraday's law when over-broadly interpreted. A wire (solid red lines) connects to two touching metal plates (silver) to form a circuit. The whole system sits in a uniform magnetic field, normal to the page. If the word "circuit" is interpreted as "primary path of current flow" (marked in red), then the magnetic flux through the "circuit" changes dramatically as the plates are rotated, yet the EMF is almost zero, which contradicts Faraday's law. After ''Feynman Lectures on Physics'' Vol. II page 17-3. |
|||
</gallery> |
|||
Although Faraday's law is always true for loops of thin wire, it can give the wrong result if naively extrapolated to other contexts.<ref name=Feynman/> One example is the [[homopolar generator]] (above left): A spinning circular metal disc in a homogeneous magnetic field generates a DC (constant in time) EMF. In Faraday's law, EMF is the time-derivative of flux, so a DC EMF is only possible if the magnetic flux is getting uniformly larger and larger perpetually. But in the generator, the magnetic field is constant and the disc stays in the same position, so no magnetic fluxes are growing larger and larger. So this example cannot be analyzed directly with Faraday's law. |
|||
Another example, due to Feynman,<ref name=Feynman/> has a dramatic change in flux through a circuit, even though the EMF is arbitrarily small. See figure and caption above right. |
|||
In both these examples, the changes in the current path are different from the motion of the material making up the circuit. The electrons in a material tend to follow the motion of the atoms that make up the material, due to [[scattering]] in the bulk and [[work function]] confinement at the edges. Therefore, motional EMF is generated when a material's atoms are moving through a magnetic field, dragging the electrons with them, thus subjecting the electrons to the [[Lorentz force]]. In the homopolar generator, the material's atoms are moving, even though the overall geometry of the circuit is staying the same. In the second example, the material's atoms are almost stationary, even though the overall geometry of the circuit is changing dramatically. On the other hand, Faraday's law always holds for thin wires, because there the geometry of the circuit always changes in a direct relationship to the motion of the material's atoms. |
|||
Although Faraday's law does not apply to all situations, the [[Maxwell–Faraday equation]] and [[Lorentz force law]] are always correct and can always be used directly.<ref name=Feynman/> |
|||
Both of the above examples can be correctly worked by choosing the appropriate path of integration for Faraday's law. Outside of context of thin wires, the path must never be chosen to go through the conductor in the shortest direct path. This is explained in detail in "The Electromagnetodynamics of Fluid" by W. F. Hughes and F. J. Young, John Wiley Inc. (1965). |
|||
==Faraday's law and relativity== |
|||
===Two phenomena=== |
|||
Some physicists have remarked that Faraday's law is a single equation describing two different phenomena: the ''motional EMF'' generated by a magnetic force on a moving wire (see [[Lorentz force#Force on a current-carrying wire|Lorentz force]]), and the ''transformer EMF'' generated by an electric force due to a changing magnetic field (due to the [[#Maxwell–Faraday equation|Maxwell–Faraday equation]]). |
|||
[[James Clerk Maxwell]] drew attention to this fact in his 1861 paper ''[[:File:On Physical Lines of Force.pdf|On Physical Lines of Force]]''. In the latter half of Part II of that paper, Maxwell gives a separate physical explanation for each of the two phenomena. |
|||
A reference to these two aspects of electromagnetic induction is made in some modern textbooks.<ref name=Griffiths1>{{cite book|author=Griffiths, David J.|title=Introduction to Electrodynamics|url=http://www.amazon.com/gp/reader/013805326X/ref=sib_dp_pt/104-2951702-6987112#reader-link|edition=Third|pages=301–3|publisher=Prentice Hall|year=1999|location=Upper Saddle River NJ|isbn=0-13-805326-X}} Note that the law relating flux to EMF, which this article calls "Faraday's law", is referred to in Griffiths' terminology as the "universal flux rule". Griffiths uses the term "Faraday's law" to refer to what article calls the "Maxwell–Faraday equation". |
|||
So in fact, in the textbook, Griffiths' statement is about the "universal flux rule".</ref> As Richard Feynman states:<ref name=Feynman>"The flux rule" is the terminology that Feynman uses to refer to the law relating magnetic flux to EMF.{{cite book|author=Richard Phillips Feynman, Leighton R B & Sands M L|title=The Feynman Lectures on Physics|year=2006|page=Vol. II, pp. 17-2|publisher=Pearson/Addison-Wesley|location=San Francisco|url=http://books.google.com/?id=zUt7AAAACAAJ&dq=intitle:Feynman+intitle:Lectures+intitle:on+intitle:Physics|isbn=0-8053-9049-9|nopp=true}}</ref> |
|||
{{Quotation|So the "flux rule" that the emf in a circuit is equal to the rate of change of the magnetic flux through the circuit applies whether the flux changes because the field changes or because the circuit moves (or both) ... |
|||
<br><br> |
|||
Yet in our explanation of the rule we have used two completely distinct laws for the two cases  –    <math>\stackrel{\mathbf{v\times B}}{}</math>  for "circuit moves" and   <math>\stackrel{\mathbf{\nabla \times E = - \part_t B}}{}</math>   for "field changes". |
|||
<br><br> |
|||
We know of no other place in physics where such a simple and accurate general principle requires for its real understanding an analysis in terms of ''two different phenomena''.|Richard P. Feynman, ''The Feynman Lectures on Physics''}} |
|||
===Einstein's view=== |
|||
Reflection on this apparent dichotomy was one of the principal paths that led [[Einstein]] to develop [[special relativity]]: |
|||
{{Quotation|It is known that Maxwell's electrodynamics—as usually understood at the present time—when applied to moving bodies, leads to asymmetries which do not appear to be inherent in the phenomena. Take, for example, the reciprocal electrodynamic action of a magnet and a conductor. |
|||
<br><br> |
|||
The observable phenomenon here depends only on the relative motion of the conductor and the magnet, whereas the customary view draws a sharp distinction between the two cases in which either the one or the other of these bodies is in motion. For if the magnet is in motion and the conductor at rest, there arises in the neighbourhood of the magnet an electric field with a certain definite energy, producing a current at the places where parts of the conductor are situated. |
|||
<br><br> |
|||
But if the magnet is stationary and the conductor in motion, no electric field arises in the neighbourhood of the magnet. In the conductor, however, we find an electromotive force, to which in itself there is no corresponding energy, but which gives rise—assuming equality of relative motion in the two cases discussed—to electric currents of the same path and intensity as those produced by the electric forces in the former case. |
|||
<br><br> |
|||
Examples of this sort, together with unsuccessful attempts to discover any motion of the earth relative to the "light medium," suggest that the phenomena of electrodynamics as well as of mechanics possess no properties corresponding to the idea of absolute rest. |
|||
| ''Albert Einstein'', ''On the Electrodynamics of Moving Bodies''<ref>A. Einstein, [http://www.fourmilab.ch/etexts/einstein/specrel/specrel.pdf On the Electrodynamics of Moving Bodies]</ref>}} |
|||
==See also== |
|||
{{Wikipedia books|Maxwell's equations}} |
|||
{{columns-list|3| |
|||
* [[Eddy current]] |
|||
* [[Inductance]] |
|||
* [[Maxwell's equations]] |
|||
* [[Moving magnet and conductor problem]] |
|||
* [[Alternator]] |
|||
* [[Crosstalk]] |
|||
* [[Faraday paradox]] |
|||
* [[Vector calculus]] |
|||
}} |
|||
==References== |
|||
{{Reflist|3}} |
|||
==Further reading== |
|||
* [http://books.google.com/books?id=vAsJAAAAIAAJ&printsec=frontcover&dq=intitle:a+intitle:treatise+intitle:on+intitle:electricity+intitle:an+intitle:magnetism&cad=0_1#v=onepage&q&f=false Maxwell, James Clerk (1881), ''A treatise on electricity and magnetism, Vol. II'', Chapter III, §530, p. 178.] Oxford, UK: Clarendon Press. ISBN 0-486-60637-6. |
|||
==External links== |
|||
* [http://www.magnet.fsu.edu/education/tutorials/java/electromagneticinduction/index.html A simple interactive Java tutorial on electromagnetic induction] National High Magnetic Field Laboratory |
|||
* [http://www.physics.smu.edu/~vega/em1304/lectures/lect13/lect13_f03.ppt R. Vega ''Induction: Faraday's law and Lenz's law'' - Highly animated lecture] |
|||
* [http://hyperphysics.phy-astr.gsu.edu/HBASE/hframe.html Notes from Physics and Astronomy HyperPhysics at Georgia State University] |
|||
* [http://www.learnemc.com/tutorials/Faraday/Faradays_Law.html Faraday's Law for EMC Engineers] |
|||
* [http://usna.edu/Users/physics/tank/Public/FaradaysLaw.pdf Tankersley and Mosca: ''Introducing Faraday's law''] |
|||
* [http://www.youtube.com/watch?v=nqMnDfNWlLM Lenz's Law at work]. |
|||
* [http://www.phy.hk/wiki/englishhtm/Induction.htm A free java simulation on motional EMF] |
|||
* [http://msdaif.googlepages.com/physics Two videos demonstrating Faraday's and Lenz's laws at EduMation] |
|||
{{DEFAULTSORT:Electromagnetic Induction}} |
|||
[[Category:Electrodynamics]] |
|||
[[Category:Concepts in physics]] |
|||
[[Category:Michael Faraday]] |
|||
[[Category:Maxwell's equations]] |
|||
Revision as of 23:14, 6 March 2014
| Articles about |
| Electromagnetism |
|---|
 |
Faraday's law of induction is a basic law of electromagnetism predicting how a magnetic field will interact with an electric circuit to produce an electromotive force (EMF). It is the fundamental operating principle of transformers, inductors, and many types of electrical motors, generators and solenoids.[1][2]
The Maxwell–Faraday equation is a generalisation of Faraday's law, and forms one of Maxwell's equations.
History
Faraday explained electromagnetic induction using a concept he called lines of force. However, scientists at the time widely rejected his theoretical ideas, mainly because they were not formulated mathematically.[3] An exception was Maxwell, who used Faraday's ideas as the basis of his quantitative electromagnetic theory.[3][4][5] In Maxwell's papers, the time varying aspect of electromagnetic induction is expressed as a differential equation which Oliver Heaviside referred to as Faraday's law even though it is slightly different in form from the original version of Faraday's law, and does not describe motional EMF. Heaviside's version (see Maxwell–Faraday equation below) is the form recognized today in the group of equations known as Maxwell's equations.
Faraday's law
Qualitative statement
The most widespread version of Faraday's law states:
The induced electromotive force in any closed circuit is equal to the negative of the time rate of change of the magnetic flux through the circuit.
This version of Faraday's law strictly holds only when the closed circuit is a loop of infinitely thin wire,[6] and is invalid in other circumstances as discussed below. A different version, the Maxwell–Faraday equation (discussed below), is valid in all circumstances.
Quantitative

Faraday's law of induction makes use of the magnetic flux ΦB through a hypothetical surface Σ whose boundary is a wire loop. Since the wire loop may be moving, we write Σ(t) for the surface. The magnetic flux is defined by a surface integral:
where dA is an element of surface area of the moving surface Σ(t), B is the magnetic field, and B·dA is a vector dot product (the infinitesimal amount of magnetic flux). In more visual terms, the magnetic flux through the wire loop is proportional to the number of magnetic flux lines that pass through the loop.
When the flux changes—because B changes, or because the wire loop is moved or deformed, or both—Faraday's law of induction says that the wire loop acquires an EMF, , defined as the energy available from a unit charge that has travelled once around the wire loop.[6][7][8][9] Equivalently, it is the voltage that would be measured by cutting the wire to create an open circuit, and attaching a voltmeter to the leads. According to the Lorentz force law (in SI units),
the EMF on a wire loop is:
where E is the electric field, B is the magnetic field (aka magnetic flux density, magnetic induction), dℓ is an infinitesimal arc length along the wire, and the line integral is evaluated along the wire (along the curve the conincident with the shape of the wire).
The EMF is also given by the rate of change of the magnetic flux:
- ,
where is the electromotive force (EMF) in volts and ΦB is the magnetic flux in webers. The direction of the electromotive force is given by Lenz's law.
For a tightly wound coil of wire, composed of N identical turns, each with the same ΦB, Faraday's law of induction states that[10][11]
where N is the number of turns of wire and ΦB is the magnetic flux in webers through a single loop.
Maxwell–Faraday equation

The Maxwell–Faraday equation is a generalisation of Faraday's law that states that a time-varying magnetic field is always accompanied by a spatially-varying, non-conservative electric field, and vice-versa. The Maxwell–Faraday equation is
(in SI units) where is the curl operator and again E(r, t) is the electric field and B(r, t) is the magnetic field. These fields can generally be functions of position r and time t.
The Maxwell–Faraday equation is one of the four Maxwell's equations, and therefore plays a fundamental role in the theory of classical electromagnetism. It can also be written in an integral form by the Kelvin-Stokes theorem:[12]
where, as indicated in the figure:
- Σ is a surface bounded by the closed contour ∂Σ,
- E is the electric field, B is the magnetic field.
- dℓ is an infinitesimal vector element of the contour ∂Σ,
- dA is an infinitesimal vector element of surface Σ. If its direction is orthogonal to that surface patch, the magnitude is the area of an infinitesimal patch of surface.
Both dℓ and dA have a sign ambiguity; to get the correct sign, the right-hand rule is used, as explained in the article Kelvin-Stokes theorem. For a planar surface Σ, a positive path element dℓ of curve ∂Σ is defined by the right-hand rule as one that points with the fingers of the right hand when the thumb points in the direction of the normal n to the surface Σ.
The integral around ∂Σ is called a path integral or line integral.
Notice that a nonzero path integral for E is different from the behavior of the electric field generated by charges. A charge-generated E-field can be expressed as the gradient of a scalar field that is a solution to Poisson's equation, and has a zero path integral. See gradient theorem.
The integral equation is true for any path ∂Σ through space, and any surface Σ for which that path is a boundary.
If the path Σ is not changing in time, the equation can be rewritten:
The surface integral at the right-hand side is the explicit expression for the magnetic flux ΦB through Σ.
Proof of Faraday's law
The four Maxwell's equations (including the Maxwell–Faraday equation), along with the Lorentz force law, are a sufficient foundation to derive everything in classical electromagnetism.[6][7] Therefore it is possible to "prove" Faraday's law starting with these equations.[13][14] Click "show" in the box below for an outline of this proof. (In an alternative approach, not shown here but equally valid, Faraday's law could be taken as the starting point and used to "prove" the Maxwell–Faraday equation and/or other laws.)
Outline of proof of Faraday's law from Maxwell's equations and the Lorentz force law. Consider the time-derivative of flux through a possibly moving loop, with area : The integral can change over time for two reasons: The integrand can change, or the integration region can change. These add linearly, therefore:
where t0 is any given fixed time. We will show that the first term on the right-hand side corresponds to transformer EMF, the second to motional EMF (see above). The first term on the right-hand side can be rewritten using the integral form of the Maxwell–Faraday equation:
Area swept out by vector element dℓ of curve ∂Σ in time dt when moving with velocity v. Next, we analyze the second term on the right-hand side:
This is the most difficult part of the proof; more details and alternate approaches can be found in references.[13][14][15] As the loop moves and/or deforms, it sweeps out a surface (see figure on right). The magnetic flux through this swept-out surface corresponds to the magnetic flux that is either entering or exiting the loop, and therefore this is the magnetic flux that contributes to the time-derivative. (This step implicitly uses Gauss's law for magnetism: Since the flux lines have no beginning or end, they can only get into the loop by getting cut through by the wire.) As a small part of the loop moves with velocity v for a short time , it sweeps out a vector area vector . Therefore, the change in magnetic flux through the loop here is
Therefore:
where v is the velocity of a point on the loop .
Putting these together,
Meanwhile, EMF is defined as the energy available per unit charge that travels once around the wire loop. Therefore, by the Lorentz force law,
Combining these,
"Counterexamples" to Faraday's law
-
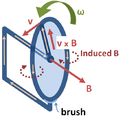
Faraday's disc electric generator. The disc rotates with angular rate ω, sweeping the conducting radius circularly in the static magnetic field B. The magnetic Lorentz force v × B drives the current along the conducting radius to the conducting rim, and from there the circuit completes through the lower brush and the axle supporting the disc. This device generates an EMF and a current, although the shape of the "circuit" is constant and thus the flux through the circuit does not change with time.
-
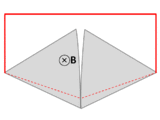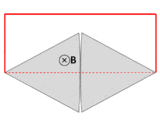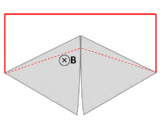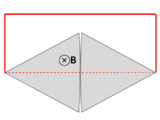
A counterexample to Faraday's law when over-broadly interpreted. A wire (solid red lines) connects to two touching metal plates (silver) to form a circuit. The whole system sits in a uniform magnetic field, normal to the page. If the word "circuit" is interpreted as "primary path of current flow" (marked in red), then the magnetic flux through the "circuit" changes dramatically as the plates are rotated, yet the EMF is almost zero, which contradicts Faraday's law. After Feynman Lectures on Physics Vol. II page 17-3.
Although Faraday's law is always true for loops of thin wire, it can give the wrong result if naively extrapolated to other contexts.[6] One example is the homopolar generator (above left): A spinning circular metal disc in a homogeneous magnetic field generates a DC (constant in time) EMF. In Faraday's law, EMF is the time-derivative of flux, so a DC EMF is only possible if the magnetic flux is getting uniformly larger and larger perpetually. But in the generator, the magnetic field is constant and the disc stays in the same position, so no magnetic fluxes are growing larger and larger. So this example cannot be analyzed directly with Faraday's law.
Another example, due to Feynman,[6] has a dramatic change in flux through a circuit, even though the EMF is arbitrarily small. See figure and caption above right.
In both these examples, the changes in the current path are different from the motion of the material making up the circuit. The electrons in a material tend to follow the motion of the atoms that make up the material, due to scattering in the bulk and work function confinement at the edges. Therefore, motional EMF is generated when a material's atoms are moving through a magnetic field, dragging the electrons with them, thus subjecting the electrons to the Lorentz force. In the homopolar generator, the material's atoms are moving, even though the overall geometry of the circuit is staying the same. In the second example, the material's atoms are almost stationary, even though the overall geometry of the circuit is changing dramatically. On the other hand, Faraday's law always holds for thin wires, because there the geometry of the circuit always changes in a direct relationship to the motion of the material's atoms.
Although Faraday's law does not apply to all situations, the Maxwell–Faraday equation and Lorentz force law are always correct and can always be used directly.[6]
Both of the above examples can be correctly worked by choosing the appropriate path of integration for Faraday's law. Outside of context of thin wires, the path must never be chosen to go through the conductor in the shortest direct path. This is explained in detail in "The Electromagnetodynamics of Fluid" by W. F. Hughes and F. J. Young, John Wiley Inc. (1965).
Faraday's law and relativity
Two phenomena
Some physicists have remarked that Faraday's law is a single equation describing two different phenomena: the motional EMF generated by a magnetic force on a moving wire (see Lorentz force), and the transformer EMF generated by an electric force due to a changing magnetic field (due to the Maxwell–Faraday equation).
James Clerk Maxwell drew attention to this fact in his 1861 paper On Physical Lines of Force. In the latter half of Part II of that paper, Maxwell gives a separate physical explanation for each of the two phenomena.
A reference to these two aspects of electromagnetic induction is made in some modern textbooks.[16] As Richard Feynman states:[6]
So the "flux rule" that the emf in a circuit is equal to the rate of change of the magnetic flux through the circuit applies whether the flux changes because the field changes or because the circuit moves (or both) ...
Yet in our explanation of the rule we have used two completely distinct laws for the two cases – for "circuit moves" and for "field changes".
We know of no other place in physics where such a simple and accurate general principle requires for its real understanding an analysis in terms of two different phenomena.
— Richard P. Feynman, The Feynman Lectures on Physics
Einstein's view
Reflection on this apparent dichotomy was one of the principal paths that led Einstein to develop special relativity:
It is known that Maxwell's electrodynamics—as usually understood at the present time—when applied to moving bodies, leads to asymmetries which do not appear to be inherent in the phenomena. Take, for example, the reciprocal electrodynamic action of a magnet and a conductor.
The observable phenomenon here depends only on the relative motion of the conductor and the magnet, whereas the customary view draws a sharp distinction between the two cases in which either the one or the other of these bodies is in motion. For if the magnet is in motion and the conductor at rest, there arises in the neighbourhood of the magnet an electric field with a certain definite energy, producing a current at the places where parts of the conductor are situated.
But if the magnet is stationary and the conductor in motion, no electric field arises in the neighbourhood of the magnet. In the conductor, however, we find an electromotive force, to which in itself there is no corresponding energy, but which gives rise—assuming equality of relative motion in the two cases discussed—to electric currents of the same path and intensity as those produced by the electric forces in the former case.
Examples of this sort, together with unsuccessful attempts to discover any motion of the earth relative to the "light medium," suggest that the phenomena of electrodynamics as well as of mechanics possess no properties corresponding to the idea of absolute rest.— Albert Einstein, On the Electrodynamics of Moving Bodies[17]
See also
References
- ^ Sadiku, M. N. O. (2007). Elements of Electromagnetics (fourth ed.). New York (USA)/Oxford (UK): Oxford University Press. p. 386. ISBN 0-19-530048-3.
- ^ "Applications of electromagnetic induction". Boston University. 1999-07-22.
- ^ a b Michael Faraday, by L. Pearce Williams, p. 510
- ^ Maxwell, James Clerk (1904), A Treatise on Electricity and Magnetism, Vol. II, Third Edition. Oxford University Press, pp. 178–9 and 189.
- ^ "Archives Biographies: Michael Faraday", The Institution of Engineering and Technology.
- ^ a b c d e f g "The flux rule" is the terminology that Feynman uses to refer to the law relating magnetic flux to EMF.Richard Phillips Feynman, Leighton R B & Sands M L (2006). The Feynman Lectures on Physics. San Francisco: Pearson/Addison-Wesley. Vol. II, pp. 17-2. ISBN 0-8053-9049-9.
{{cite book}}: Unknown parameter|nopp=ignored (|no-pp=suggested) (help) - ^ a b Griffiths, David J. (1999). Introduction to Electrodynamics (Third ed.). Upper Saddle River NJ: Prentice Hall. pp. 301–303. ISBN 0-13-805326-X.
- ^ Tipler and Mosca, Physics for Scientists and Engineers, p795, google books link
- ^ Note that different textbooks may give different definitions. The set of equations used throughout the text was chosen to be compatible with the special relativity theory.
- ^ Essential Principles of Physics, P.M. Whelan, M.J. Hodgeson, 2nd Edition, 1978, John Murray, ISBN 0-7195-3382-1
- ^ Nave, Carl R. "Faraday's Law". HyperPhysics. Georgia State University. Retrieved 29 August 2011.
- ^ Roger F Harrington (2003). Introduction to electromagnetic engineering. Mineola, NY: Dover Publications. p. 56. ISBN 0-486-43241-6.
- ^ a b Attention: This template ({{cite doi}}) is deprecated. To cite the publication identified by doi:10.1119/1.1987339, please use {{cite journal}} (if it was published in a bona fide academic journal, otherwise {{cite report}} with
|doi=10.1119/1.1987339instead. - ^ a b Basic Theoretical Physics: A Concise Overview by Krey and Owen, p155, google books link
- ^ K. Simonyi, Theoretische Elektrotechnik, 5th edition, VEB Deutscher Verlag der Wissenschaften, Berlin 1973, equation 20, page 47
- ^ Griffiths, David J. (1999). Introduction to Electrodynamics (Third ed.). Upper Saddle River NJ: Prentice Hall. pp. 301–3. ISBN 0-13-805326-X. Note that the law relating flux to EMF, which this article calls "Faraday's law", is referred to in Griffiths' terminology as the "universal flux rule". Griffiths uses the term "Faraday's law" to refer to what article calls the "Maxwell–Faraday equation". So in fact, in the textbook, Griffiths' statement is about the "universal flux rule".
- ^ A. Einstein, On the Electrodynamics of Moving Bodies
Further reading
- Maxwell, James Clerk (1881), A treatise on electricity and magnetism, Vol. II, Chapter III, §530, p. 178. Oxford, UK: Clarendon Press. ISBN 0-486-60637-6.
External links
- A simple interactive Java tutorial on electromagnetic induction National High Magnetic Field Laboratory
- R. Vega Induction: Faraday's law and Lenz's law - Highly animated lecture
- Notes from Physics and Astronomy HyperPhysics at Georgia State University
- Faraday's Law for EMC Engineers
- Tankersley and Mosca: Introducing Faraday's law
- Lenz's Law at work.
- A free java simulation on motional EMF
- Two videos demonstrating Faraday's and Lenz's laws at EduMation