Talk:Dispersion (optics): Difference between revisions
GVD |
|||
| Line 117: | Line 117: | ||
== GVD == |
== GVD == |
||
Hi Stevej, Your recent edits to the lead could be read as meaning that ''dispersion'' and ''group velocity dispersion'' are the same thing. They are of course interdependent, but if you quantify them, then in general they'll be different numbers. If the dispersion relation was something like <math>\omega = \omega_0 + A \beta</math> (over a limited band obviously), then there would be "''phase velocity dispersion''", but no ''group velocity dispersion''. Regarding periodic structures; each space-harmonic of a given mode has the same group velocity, and a different phase velocity (but it still has a well-defined phase velocity).--[[User:Catslash|catslash]] ([[User talk:Catslash|talk]]) 00:17, 9 April 2009 (UTC) |
Hi Stevej, Your recent edits to the lead could be read as meaning that ''dispersion'' and ''group velocity dispersion'' are the same thing. They are of course interdependent, but if you quantify them, then in general they'll be different numbers. If the dispersion relation was something like <math>\omega = \omega_0 + A \beta</math> (over a limited band obviously), then there would be "''phase velocity dispersion''", but no ''group velocity dispersion''. Regarding periodic structures; each space-harmonic of a given mode has the same group velocity, and a different phase velocity (but it still has a well-defined phase velocity).--[[User:Catslash|catslash]] ([[User talk:Catslash|talk]]) 00:17, 9 April 2009 (UTC) |
||
== Ultrashort Optical pulses == |
|||
Something is missing to this article, namely a sub-section of travelling [[ultrashort pulse|ultrashort pulses]] and the partial differential equation that governs the carrier envelope of these pulses subject to dispersion. Such a presentation is essential. I found this out because the [[ultrashort pulse]] section has a link to this site on dispersion but the material is not sufficient. |
|||
== References == |
== References == |
||
Revision as of 02:02, 3 August 2009
| Physics C‑class High‑importance | ||||||||||
| ||||||||||
| Glass C‑class High‑importance | ||||||||||
| ||||||||||
Material dispersion in optics
Is this correct:
"that is, refractive index n decreases with increasing wavelength λ. In this case, the medium is said to have normal dispersion. Whereas, if the index increases with decreasing wavelength the medium has anomalous dispersion."
Group velocity formula
I recently added what I thought was the more general formula for the group velocity:
which user:Stevenj has removed saying it's not generally true, only in the case of low dispersion. I though this came from the definition of the phase and group velocities:
and
hence:
and from , giving:
- .
So, what am I missing? Are my velocity definitions wrong? (I accept that none of the equations are valid for inhomogeneous media.) -- Bob Mellish 17:58, 5 October 2005 (UTC)
- Ah, now I see what you meant. My problem is with the . Ordinarily, in equations like this (or in most of optics for that matter) λ means the vacuum wavelength, i.e. . Using the wavelength in the material is problematic — not only for inhomogeneous media, but also for anisotropic homogeneous media — but mainly I think people don't use the medium-dependent λ because it is just more convenient to talk in terms of conserved quantities. (I wish this article would start with the general definitions and then give the specific formulas for special cases like homogeneous media, but I don't have time to do major re-working myself right now.) —Steven G. Johnson 04:59, 6 October 2005 (UTC)
- It looks like essentially every usage of λ in the article means vacuum wavelength, but it never says that explicitly. Sigh. —Steven G. Johnson 05:02, 6 October 2005 (UTC)
- Hrrm, I didn't think of k being wrong. Yes, vacuum wavelength makes more sense to use. Unfortunately I've forgotten most of the derviation of this stuff, if you've got a good modern reference I could look it up and try to improve the article, if you're too busy. Personally I'd prefer it to start with the simple cases and move to the most complex ones, but then I've never worked with photonic crystals or the like. -- Bob Mellish 16:35, 7 October 2005 (UTC)
The classic reference on all of this stuff is:
- Léon Brillouin, Wave Propagation and Group Velocity (Academic: New York, 1960).
You can also find some discussion in Jackson (Classical Electrodynamics) etc. However, even so most of this discussion is limited to homogeneous media. In general, the group velocity is defined as dω/dk, where k is the Bloch wavevector in a periodic system (of which a homogeneous system is a special case). In a periodic system, on the other hand, there is no perfectly satisfactory definition of phase velocity, since k is only defined up to a reciprocal lattice vector. A proof that dω/dk is equal to the energy velocity for dispersionless, lossless systems (including periodic systems and also including waveguides) can be found in Sakoda, Optical Properties of Photonic Crystals (Springer: Berlin, 2001). This can be extended to systems with material dispersion (using the proper definition of energy density in a dispersive medium, as can be found in Jackson), but I'm not aware of any single reference that contains the complete derivation for all cases (arbitrary inhomogeneity and dispersion). Once you include loss, of course, or when you are looking at evanescent modes (complex k), then the group velocity is no longer the energy velocity; this is described in the Brillouin reference, which also describes the front velocity and other concepts. A good description (without too much math) of the phenomena and consequences of dispersion (both material and waveguide, but not in general periodic media) in communications systems can be found in Ramaswami and Sivarajan, Optical Networks: A Practical Perspective (Academic Press, 1998); this is an excellent introductory textbook overall (although a little specialized to fibers, in which things simplify because the inhomogeneity is weak). In particular, Ramaswami also gives a more general definition of the dispersion parameter D, which is especially pertinent to this article. —Steven G. Johnson 18:49, 7 October 2005 (UTC)
- Heh, I actually have the Brillouin book right here; I grabbed that equation from page 3 (eqn. 9b). I've been reading it with aim to improving the front velocity and signal velocity articles. I'll try seeing if the library has the other works you mention. -- Bob Mellish 18:59, 7 October 2005 (UTC)
- To Steve/Bob: So is the equation v(group) = v(phase) - lambda*[d(v(phase))/d(lambda)] , true always? If yes, the correct expression for v(group) in terms of the refractive index is : v(group) = c*[(1/n) + (lambda)*(d(n)/d(lambda))/n^2], which is only approximately equal (upto first order term) to the formula typed out in the article currently i.e. v(group) = c*[n - (lambda)*(d(n)/d(lambda))]^(-1). So which one is the correct formula and which one is the approximate one? -- Mvpranav —Preceding unsigned comment added by Mvpranav (talk • contribs) 23:28, 10 December 2008 (UTC)
How to solve a problem of light dispersion in Optics?
waveguide dispersion vs. modal dispersion
what's the difference? Pfalstad 15:47, 4 January 2006 (UTC)
- Modal dispersion comes because the waveguide supports multiple modes at the same frequency that travel at different speeds. Waveguide dispersion refers to the fact that for a single mode the speed depends on the relative size of the wavelength and the waveguide geometry, which causes the solution's field pattern to change. —Steven G. Johnson 17:37, 4 January 2006 (UTC)
Dark Side of the Moon
Anyone agree with a mention or even a photo of Pink Floyd's album Dark Side of the Moon, which of course featured dispersion on the cover? Wwwhhh 02:37, 27 July 2006 (UTC)
Conceptual animation
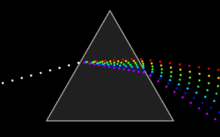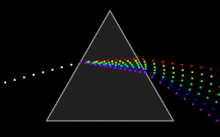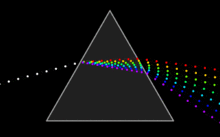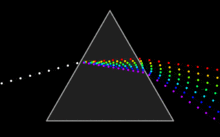
I thought we could use something more visually appealing to explain dispersion, so I came up with this little animation. Maybe it's too conceptual to the point of being entirely misleading, so I'm putting it here first so you can be the judge. Oh, and if I screwed up with anything, keep in mind I've been awake for 30 hours. :P — Kieff 21:05, 20 January 2007 (UTC)
- Nice animation, but has a couple of issues. (1) the refraction angles at the left and right surfaces don't match. The green component (3rd from above) travels through the glass horizontally, which means that it should come out at the same angle as how it went in. (2) The ratios of the velocities inside/outside the prism don't seem to match the refraction angles, although i didn't check very carefully. If you draw the light as wavefronts rather than dots - or as two rows of dots - , both (1) and (2) should be satisfied. I think this type of properties should be visualised correctly. Although it would require the GIF animation to be an enormous number of frames, which would be a disadvantage. (3) Using a prism for visualisation actually demonstrates two effects at the same time: temporal dispersion and refraction. It might actually be more to the point to only have a beam traveling through a slab or rod of glass rather than a prism. Han-Kwang 21:04, 19 March 2007 (UTC)
Posted this earlier onver on the image page 65.202.227.114 (talk)mjd 2008-03-14 09:14EDT I think the "refracting dots" model is more intuitive, but there are some issues that I think should be considered. Your white dots entering the left side of the prism could be considered light "packets" and as such have a wavefront associated with them. They may or may not be coherent - which is unimportant - but they have a definite phase relationship associate with the wavefront, which is also approximately a plane wave. The chromatic dots leaving the prism have a curved wavefront which is exactly correct, and both the curvature and overall tilt of the wavefront are very instructive. What happens inside the prism is quite a bit more problematic. An inquisitive student would notice that the various wavefronts entering the prism are segregated and recombined into new wavefronts before exiting the prism, which is of cource incorrect. It is precisely that the wavefront itself is refracted according to wavelength or frequency in the material that is the take-home message for this sub-topic, and one that great pains should be taken to illustrate correctly. Wonderful graphical work, in any event. 65.202.227.91 (talk) 18:22, 6 March 2008 (UTC)mjd 2008-03-06 13:21EST
Retrieved from "http://en.wikipedia.org/wiki/Image_talk:Light_dispersion_conceptual.gif"

A version with waves is now available. — Kieff | Talk 04:16, 24 December 2007 (UTC)
The version with waves is flawed and should not be used. The red rays are clearly moving faster than the purple ones outside the prism. Unless the space outside the prism is supposed to be some odd medium with very high dispersion, this is incorrect. The version of the image with little balls had this detail correct.--Srleffler (talk) 00:11, 17 February 2008 (UTC)- This is now fixed. — Kieff | Talk 03:36, 27 February 2008 (UTC)
Measuring Dispersion
Hi, I wanted to add a part about measuring waveguide dispersion. do you think it should be a new page or a part of this page? Sr903 20:28, 19 March 2007 (UTC)
- I'd say Waveguide is a better place to discuss dispersion in waveguides. I actually think the waveguide discussion should not be so prominent at the top of this page, but rather in a section, but I might be biased by my background in spectroscopy rather than telecom. Han-Kwang 21:04, 19 March 2007 (UTC)
- I see your point but as someone from more of a telecom background. How about a page named Waveguide Dispersion? We could then redirect Fiber Optic Dispersion. In the Telecom world Dispersion is a big thing and I would expect to see the amount of content on this subject growing.Sr903 14:19, 20 March 2007 (UTC)
- Any comprehensive discussion of dispersion has to include both material dispersion and structural (a.k.a. waveguide) dispersion. One problem with the current page, however, is that the discussion of waveguide dispersion is misleading. "Waveguide dispersion" isn't just any dispersion that happens to take place in a waveguide. It's dispersion that occurs because you have a waveguide, which breaks the scale-invariance with respect to the wavelength, and it happens in addition to material dispersion (although they aren't literally additive except in low-contrast media such as doped-core fibers...the combination is more complicated in general). More generally, you get structural dispersion in any inhomogeneous medium that is periodic or uniform along the direction of propagation (which is necessary to get a well-defined group velocity).
- There are other problems with the current page as well, for example it pointlessly specializes the equations of group velocity and the dispersion parameter to homogeneous media, rather than starting with the general definitions.
- Group-velocity dispersion is a very general phenomenon. An encyclopedia article on such a general phenomenon should describe its general features, definitions, and sources first, and then give more detailed equations for specialized cases like homogeneous materials, doped-core optical fibers, etcetera, possibly in sub-articles. The top-level article should most certainly not be written from a narrow perspective, but this is unfortunately the present situation.
Is it just me, or doesn't the page specify what are the units of dispresion? (Ran Shenhar 2 May 2007)
- I added the general definition of the dispersion parameter D, including waveguide and material dispersion, and the physical interpretation as pulse spreading per unit distance per unit bandwidth, and the typical units (for optical fibers) of ps / nm km. —Steven G. Johnson (talk) 04:51, 17 February 2008 (UTC)
Merge to Refraction?
Much of this article is about what I understand to be refraction. Refraction concepts are included, such as refractive index, without explanation except by way of link. Even if the articles are not merged, there should at least be some discussion of the relation between dispersion and refraction; how they are the same and how they are different. Robert P. O'Shea (talk) 14:43, 20 March 2008 (UTC)
- I'd say there isn't much connection between dispersion and refraction; you can have either without the other. The Material dispersion in optics section explains the effect of dispersion on refraction (i.e. it gives rise to angular dispersion). The other sections don't relate to refraction at all, except for the very small Dispersion in gemology and Dispersion in imaging sections. Maybe these should be sub-sections of Material dispersion in optics? Perhaps the prism picture in the lead is suggestive of a stronger connection with refraction than is apparent from reading the whole article. --catslash (talk) 15:25, 20 March 2008 (UTC)
- I agree, they are independent concepts. One can have refraction in a non-dispersive medium. One can also have dispersion without refraction (e.g. we talk about material dispersion and pulse spreading in a homogeneous medium, where there are no interfaces to refract through; another example would be waveguide dispersion in a hollow metallic waveguide, where there is reflection but no refraction). —Steven G. Johnson (talk) 15:39, 20 March 2008 (UTC)
- Thanks for clarifying the difference. But my point stands. Essentially all of the introductory paragraphs of the article describe what most people would understand as refraction. There needs to be some reconciliation in the article of the two concepts, rather than simply confining it to the discussion. I've put back the mergeto note as a bookmark to people who know that the two concepts are different to explain how in the article and as a bookmark to people who don't know that the two concepts are different to see some deficiencies in this article. Robert P. O'Shea (talk) 09:39, 2 April 2008 (UTC)
- I've modified the introduction to make it clear that prisms/rainbows are just one familiar example of a dispersion phenomenon, and are by no means the only example. (Still, even for the original version of the intro, your comment was hyperbole—exactly two sentences referred to prisms/refractions, and both sentences gave them as examples; the rest of the intro did not mention refraction at all.) —Steven G. Johnson (talk) 04:13, 3 April 2008 (UTC)
Group velocity dispersion formula wrong
The equation
looks wrong, like a mixup between two correct versions:
- where is frequency
I'd prefer the latter, which is found at page 962 in the book "Fundamentals of Photonics" by B.E.A. Saleh & M.C Teich (Wiley-interscience 2007). and are the values in vacuum. Assuming --ErikM (talk) 10:54, 8 January 2009 (UTC)
Maybe there are two different conventions, depending on if you use the sign from a frequency derivative of a wavelength derivative. The article now says If D is less than zero, the medium is said to have positive dispersion. If D is greater than zero, the medium has negative dispersion. but with the formula from Saleh & Teich[1] (actually for what they call ) the naming seems more reasonable: If D is less than zero, the medium is said to have negative dispersion. If D is greater than zero, the medium has positive dispersion. —Preceding unsigned comment added by ErikM (talk • contribs) 11:10, 8 January 2009 (UTC)
- The formula in the article is correct. Your formula is also correct. They correspond to different definitions of the dispersion parameter D. Both definitions are given in Saleh and Teich. I think you have a different edition of Saleh than mine because our page numbers don't match up. Saleh calls the definition you are using (equation 5.6-20 in my edition) and the definition the Wikipedia article uses (equation 5.6-21 in my edition). The latter definition is more widely used in the fiber/telecom industry. Also, the latter definition corresponds to the more general definition given in the Wikipedia article (generalized to inhomogeneous media, i.e. including both material and waveguide dispersion):[2]
- To get the homogeneous-medium equation in the article, substitute and recall via the chain rule that . The definition you are using corresponds more generally to:
- (equation 5.6-9 in my edition of Saleh). The difference is whether one wants to describe pulse spreading per unit frequency bandwidth () or per unit wavelength bandwidth (), as explained in Saleh. —Steven G. Johnson (talk) 19:13, 8 January 2009 (UTC)
GVD
Hi Stevej, Your recent edits to the lead could be read as meaning that dispersion and group velocity dispersion are the same thing. They are of course interdependent, but if you quantify them, then in general they'll be different numbers. If the dispersion relation was something like (over a limited band obviously), then there would be "phase velocity dispersion", but no group velocity dispersion. Regarding periodic structures; each space-harmonic of a given mode has the same group velocity, and a different phase velocity (but it still has a well-defined phase velocity).--catslash (talk) 00:17, 9 April 2009 (UTC)
Ultrashort Optical pulses
Something is missing to this article, namely a sub-section of travelling ultrashort pulses and the partial differential equation that governs the carrier envelope of these pulses subject to dispersion. Such a presentation is essential. I found this out because the ultrashort pulse section has a link to this site on dispersion but the material is not sufficient.
References
(--ErikM (talk) 11:14, 8 January 2009 (UTC)) The Wikipedia article on Kramers-Kronig relations links to this article and that article back to this one. But other than that, there is no reference to Kramers-Kronig on this page. What gives? This is not a useful reference. Nor do I see any formula on this page that even remotely looks like a Kramer-Kronig Formula. 67.95.202.34 (talk) 04:33, 7 February 2009 (UTC)




















