Fuzzy logic: Difference between revisions

Content deleted Content added

Inline

Revision as of 09:00, 25 April 2010

Fuzzy logic is a form of multi-valued logic derived from fuzzy set theory to deal with reasoning that is approximate rather than precise. In contrast with "crisp logic", where binary sets have binary logic, fuzzy logic variables may have a truth value that ranges between 0 and 1 and is not constrained to the two truth values of classic propositional logic.^[1] Furthermore, when linguistic variables are used, these degrees may be managed by specific functions.

Fuzzy logic emerged as a consequence of the 1965 proposal of fuzzy set theory by Lotfi Zadeh.^[2]^[3] Though fuzzy logic has been applied to many fields, from control theory to artificial intelligence, it still remains controversial among most statisticians, who prefer Bayesian logic, and some control engineers, who prefer traditional two-valued logic.

Degrees of truth

Fuzzy logic and probabilistic logic are mathematically similar – both have truth values ranging between 0 and 1 – but conceptually distinct, due to different interpretations -- see interpretations of probability theory. Fuzzy logic corresponds to "degrees of truth", while probabilistic logic corresponds to "probability, likelihood"; as these differ, fuzzy logic and probabilistic logic yield different models of the same real-world situations.

Both degrees of truth and probabilities range between 0 and 1 and hence may seem similar at first. For example, let a 100 ml glass contain 30 ml of water. Then we may consider two concepts: Empty and Full. The meaning of each of them can be represented by a certain fuzzy set. Then one might define the glass as being 0.7 empty and 0.3 full. Note that the concept of emptiness would be subjective and thus would depend on the observer or designer. Another designer might equally well design a set membership function where the glass would be considered full for all values down to 50 ml. It is essential to realize that fuzzy logic uses truth degrees as a mathematical model of the vagueness phenomenon while probability is a mathematical model of randomness. A probabilistic setting would first define a scalar variable for the fullness of the glass, and second, conditional distributions describing the probability that someone would call the glass full given a specific fullness level. This model, however, has no sense without accepting occurrence of some event, e.g. that after a few minutes, the glass will be half empty. Note that the conditioning can be achieved by having a specific observer that randomly selects the level for the glass, a distribution over deterministic observers, or both. Consequently, probability has nothing in common with fuzziness, these are simply different concepts which superficially seem similar because of using the same unit interval of real numbers [0,1]. Still, since theorems such as De Morgan's have dual applicability and properties of random variables are analogous to properties of binary logic states, one can see where the confusion might arise.

Applying truth values

A basic application might characterize subranges of a continuous variable. For instance, a temperature measurement for anti-lock brakes might have several separate membership functions defining particular temperature ranges needed to control the brakes properly. Each function maps the same temperature value to a truth value in the 0 to 1 range. These truth values can then be used to determine how the brakes should be controlled.

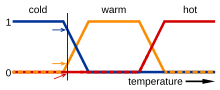
In this image, the meaning of the expressions cold, warm, and hot is represented by functions mapping a temperature scale. A point on that scale has three "truth values" — one for each of the three functions. The vertical line in the image represents a particular temperature that the three arrows (truth values) gauge. Since the red arrow points to zero, this temperature may be interpreted as "not hot". The orange arrow (pointing at 0.2) may describe it as "slightly warm" and the blue arrow (pointing at 0.8) "fairly cold".

Linguistic variables

While variables in mathematics usually take numerical values, in fuzzy logic applications, the non-numeric linguistic variables are often used to facilitate the expression of rules and facts.^[4]

A linguistic variable such as age may have a value such as young or its antonym old. However, the great utility of linguistic variables is that they can be modified via linguistic hedges applied to primary terms. The linguistic hedges can be associated with certain functions. For example, L. A. Zadeh proposed to take the square of the membership function. This model, however, does not work properly. For more details, see the references.

Example

Fuzzy set theory defines fuzzy operators on fuzzy sets. The problem in applying this is that the appropriate fuzzy operator may not be known. For this reason, fuzzy logic usually uses IF-THEN rules, or constructs that are equivalent, such as fuzzy associative matrices.

Rules are usually expressed in the form:
IF variable IS property THEN action

For example, a simple temperature regulator that uses a fan might look like this:

IF temperature IS very cold THEN stop fan
IF temperature IS cold THEN turn down fan
IF temperature IS normal THEN maintain level
IF temperature IS hot THEN speed up fan

There is no "ELSE" – all of the rules are evaluated, because the temperature might be "cold" and "normal" at the same time to different degrees.

The AND, OR, and NOT operators of boolean logic exist in fuzzy logic, usually defined as the minimum, maximum, and complement; when they are defined this way, they are called the Zadeh operators. So for the fuzzy variables x and y:

NOT x = (1 - truth(x))
x AND y = minimum(truth(x), truth(y))
x OR y = maximum(truth(x), truth(y))

There are also other operators, more linguistic in nature, called hedges that can be applied. These are generally adverbs such as "very", or "somewhat", which modify the meaning of a set using a mathematical formula.

Logical analysis

In mathematical logic, there are several formal systems of "fuzzy logic"; most of them belong among so-called t-norm fuzzy logics.

Propositional fuzzy logics

The most important propositional fuzzy logics are:

Monoidal t-norm-based propositional fuzzy logic MTL is an axiomatization of logic where conjunction is defined by a left continuous t-norm, and implication is defined as the residuum of the t-norm. Its models correspond to MTL-algebras that are prelinear commutative bounded integral residuated lattices.
Basic propositional fuzzy logic BL is an extension of MTL logic where conjunction is defined by a continuous t-norm, and implication is also defined as the residuum of the t-norm. Its models correspond to BL-algebras.
Łukasiewicz fuzzy logic is the extension of basic fuzzy logic BL where standard conjunction is the Łukasiewicz t-norm. It has the axioms of basic fuzzy logic plus an axiom of double negation, and its models correspond to MV-algebras.
Gödel fuzzy logic is the extension of basic fuzzy logic BL where conjunction is Gödel t-norm. It has the axioms of BL plus an axiom of idempotence of conjunction, and its models are called G-algebras.
Product fuzzy logic is the extension of basic fuzzy logic BL where conjunction is product t-norm. It has the axioms of BL plus another axiom for cancellativity of conjunction, and its models are called product algebras.
Fuzzy logic with evaluated syntax (sometimes also called Pavelka's logic), denoted by EVŁ, is a further generalization of mathematical fuzzy logic. While the above kinds of fuzzy logic have traditional syntax and many-valued semantics, in EVŁ is evaluated also syntax. This means that each formula has an evaluation. Axiomatization of EVŁ stems from Łukasziewicz fuzzy logic. A generalization of classical Gödel completeness theorem is provable in EVŁ.

Predicate fuzzy logics

These extend the above-mentioned fuzzy logics by adding universal and existential quantifiers in a manner similar to the way that predicate logic is created from propositional logic. The semantics of the universal (resp. existential) quantifier in t-norm fuzzy logics is the infimum (resp. supremum) of the truth degrees of the instances of the quantified subformula.

Decidability issues for fuzzy logic

The notions of a "decidable subset" and "recursively enumerable subset" are basic ones for classical mathematics and classical logic. Then, the question of a suitable extension of such concepts to fuzzy set theory arises. A first proposal in such a direction was made by E.S. Santos by the notions of fuzzy Turing machine, Markov normal fuzzy algorithm and fuzzy program (see Santos 1970). Successively, L. Biacino and G. Gerla showed that such a definition is not adequate and therefore proposed the following one. Ü denotes the set of rational numbers in [0,1]. A fuzzy subset s : S $\rightarrow$ [0,1] of a set S is recursively enumerable if a recursive map h : S×N $\rightarrow$ Ü exists such that, for every x in S, the function h(x,n) is increasing with respect to n and s(x) = lim h(x,n). We say that s is decidable if both s and its complement –s are recursively enumerable. An extension of such a theory to the general case of the L-subsets is proposed in Gerla 2006. The proposed definitions are well related with fuzzy logic. Indeed, the following theorem holds true (provided that the deduction apparatus of the fuzzy logic satisfies some obvious effectiveness property).

Theorem. Any axiomatizable fuzzy theory is recursively enumerable. In particular, the fuzzy set of logically true formulas is recursively enumerable in spite of the fact that the crisp set of valid formulas is not recursively enumerable, in general. Moreover, any axiomatizable and complete theory is decidable.

It is an open question to give supports for a Church thesis for fuzzy logic claiming that the proposed notion of recursive enumerability for fuzzy subsets is the adequate one. To this aim, further investigations on the notions of fuzzy grammar and fuzzy Turing machine should be necessary (see for example Wiedermann's paper). Another open question is to start from this notion to find an extension of Gödel’s theorems to fuzzy logic.

Fuzzy databases

Once fuzzy relations are defined, it is possible to develop fuzzy relational databases. The first fuzzy relational database, FRDB, appeared in Maria Zemankova's dissertation. Later, some other models arose like the Buckles-Petry model, the Prade-Testemale Model, the Umano-Fukami model or the GEFRED model by J.M. Medina, M.A. Vila et al. In the context of fuzzy databases, some fuzzy querying languages have been defined, highlighting the SQLf by P. Bosc et al. and the FSQL by J. Galindo et al. These languages define some structures in order to include fuzzy aspects in the SQL statements, like fuzzy conditions, fuzzy comparators, fuzzy constants, fuzzy constraints, fuzzy thresholds, linguistic labels and so on.

Application areas

Fuzzy logic is used in the operation or programming of:

Air conditioners
Automobile and such vehicle subsystems as automatic transmissions, ABS and cruise control
Tokyo monorail
Cameras
Digital image processing, such as edge detection
Dishwashers
Elevators
Some microcontrollers and microprocessors (e.g. Freescale 68HC12)
Hydrometeor classification algorithms for polarimetric weather radar
Language filters on message boards and chat rooms for filtering out offensive text
The Massive engine used in the Lord of the Rings films, which allowed large-scale armies to enact random yet orderly movements
Mineral Deposit estimation
Pattern recognition in Remote Sensing
Rice cookers
Video game artificial intelligence
Home appliances (e.g. washing machine)

Comparison to probability

Fuzzy logic and probability are different ways of expressing uncertainty. While both fuzzy logic and probability theory can be used to represent subjective belief, fuzzy set theory uses the concept of fuzzy set membership (i.e., how much a variable is in a set), probability theory uses the concept of subjective probability (i.e., how probable do I think that a variable is in a set). While this distinction is mostly philosophical, the fuzzy-logic-derived possibility measure is inherently different from the probability measure, hence they are not directly equivalent. However, many statisticians are persuaded by the work of Bruno de Finetti that only one kind of mathematical uncertainty is needed and thus fuzzy logic is unnecessary. On the other hand, Bart Kosko argues that probability is a subtheory of fuzzy logic, as probability only handles one kind of uncertainty. He also claims to have proven a derivation of Bayes' theorem from the concept of fuzzy subsethood. Lotfi Zadeh argues that fuzzy logic is different in character from probability, and is not a replacement for it. He fuzzified probability to fuzzy probability and also generalized it to what is called possibility theory. (cf.^[5])

Notes

^ Novák, V., Perfilieva, I. and Močkoř, J. (1999) Mathematical principles of fuzzy logic Dodrecht: Kluwer Academic. ISBN 0-7923-8595-0
^ "Fuzzy Logic". Stanford Encyclopedia of Philosophy. Stanford University. 2006-07-23. Retrieved 2008-09-29.
^ Zadeh, L.A. (1965). "Fuzzy sets", Information and Control 8 (3): 338–353.
^ Zadeh, L. A. et al. 1996 Fuzzy Sets, Fuzzy Logic, Fuzzy Systems, World Scientific Press, ISBN 9810224214
^ Novák, V. Are fuzzy sets a reasonable tool for modeling vague phenomena?, Fuzzy Sets and Systems 156 (2005) 341—348.

Bibliography

Von Altrock, Constantin (1995). Fuzzy logic and NeuroFuzzy applications explained. Upper Saddle River, NJ: Prentice Hall PTR. ISBN 0-13-368465-2.
Biacino, L. (2002). "Fuzzy logic, continuity and effectiveness". Archive for Mathematical Logic. 41 (7): 643–667. doi:10.1007/s001530100128. ISSN 0933-5846. {{cite journal}}: Unknown parameter |coauthors= ignored (|author= suggested) (help)
Cox, Earl (1994). The fuzzy systems handbook: a practitioner's guide to building, using, maintaining fuzzy systems. Boston: AP Professional. ISBN 0-12-194270-8.
Gerla, Giangiacomo (2006). "Effectiveness and Multivalued Logics". Journal of Symbolic Logic. 71 (1): 137–162. doi:10.2178/jsl/1140641166. ISSN 0022-4812. {{cite journal}}: Cite has empty unknown parameter: |coauthors= (help)
Hájek, Petr (1998). Metamathematics of fuzzy logic. Dordrecht: Kluwer. ISBN 0792352386.
Hájek, Petr (1995). "Fuzzy logic and arithmetical hierarchy". Fuzzy Sets and Systems. 3 (8): 359–363. doi:10.1016/0165-0114(94)00299-M. ISSN 0165-0114. {{cite journal}}: Cite has empty unknown parameter: |coauthors= (help)
Halpern, Joseph Y. (2003). Reasoning about uncertainty. Cambridge, Mass: MIT Press. ISBN 0-262-08320-5.
Höppner, Frank (1999). Fuzzy cluster analysis: methods for classification, data analysis and image recognition. New York: John Wiley. ISBN 0-471-98864-2. {{cite book}}: Unknown parameter |coauthors= ignored (|author= suggested) (help)
Ibrahim, Ahmad M. (1997). Introduction to Applied Fuzzy Electronics. Englewood Cliffs, N.J: Prentice Hall. ISBN 0-13-206400-6. {{cite book}}: Cite has empty unknown parameter: |coauthors= (help)
Klir, George J. (1988). Fuzzy sets, uncertainty, and information. Englewood Cliffs, N.J: Prentice Hall. ISBN 0-13-345984-5. {{cite book}}: Unknown parameter |coauthors= ignored (|author= suggested) (help)
Klir, George J. (1997). Fuzzy set theory: foundations and applications. Englewood Cliffs, NJ: Prentice Hall. ISBN 0133410587. {{cite book}}: Unknown parameter |coauthors= ignored (|author= suggested) (help)
Klir, George J. (1995). Fuzzy sets and fuzzy logic: theory and applications. Upper Saddle River, NJ: Prentice Hall PTR. ISBN 0-13-101171-5. {{cite book}}: Unknown parameter |coauthors= ignored (|author= suggested) (help)
Kosko, Bart (1993). Fuzzy thinking: the new science of fuzzy logic. New York: Hyperion. ISBN 0-7868-8021-X.
Kosko, Bart (1993). "Fuzzy Logic". Scientific American. 269 (1): 76–81. {{cite journal}}: Unknown parameter |month= ignored (help)
Montagna, F. (2001). "Three complexity problems in quantified fuzzy logic". Studia Logica. 68 (1): 143–152. doi:10.1023/A:1011958407631. ISSN 0039-3215. {{cite journal}}: Cite has empty unknown parameter: |coauthors= (help)
Mundici, Daniele (1999). Algebraic foundations of many-valued reasoning. Dodrecht: Kluwer Academic. ISBN 0-7923-6009-5. {{cite book}}: Unknown parameter |coauthors= ignored (|author= suggested) (help)
Novák, Vilém (1989). Fuzzy Sets and Their Applications. Bristol: Adam Hilger. ISBN 0-85274-583-4.
Novák, Vilém (2005). "On fuzzy type theory". Fuzzy Sets and Systems. 149: 235–273. doi:10.1016/j.fss.2004.03.027.
Novák, Vilém (1999). Mathematical principles of fuzzy logic. Dodrecht: Kluwer Academic. ISBN 0-7923-8595-0. {{cite book}}: Unknown parameter |coauthors= ignored (|author= suggested) (help)
Passino, Kevin M. (1998). Fuzzy control. Boston: Addison-Wesley. ISBN 020118074X. {{cite book}}: Unknown parameter |coauthors= ignored (|author= suggested) (help)
Pu, Pao Ming; Liu, Ying Ming (1980), "Fuzzy topology. I. Neighborhood structure of a fuzzy point and Moore-Smith convergence", Journal of Mathematical Analysis and Applications, 76 (2): 571–599, doi:10.1016/0022-247X(80)90048-7, ISSN 0022-247X
Santos, Eugene S. (1970). "Fuzzy Algorithms". Information and Control. 17 (4): 326–339. {{cite journal}}: Cite has empty unknown parameter: |coauthors= (help)
Scarpellini, Bruno (1962). "Die Nichaxiomatisierbarkeit des unendlichwertigen Prädikatenkalküls von Łukasiewicz". Journal of Symbolic Logic. 27 (2): 159–170. doi:10.2307/2964111. ISSN 0022-4812. {{cite journal}}: Cite has empty unknown parameter: |coauthors= (help)
Steeb, Willi-Hans (2008). The Nonlinear Workbook: Chaos, Fractals, Cellular Automata, Neural Networks, Genetic Algorithms, Gene Expression Programming, Support Vector Machine, Wavelets, Hidden Markov Models, Fuzzy Logic with C++, Java and SymbolicC++ Programs: 4edition. World Scientific. ISBN 981-281-852-9.
Wiedermann, J. (2004). "Characterizing the super-Turing computing power and efficiency of classical fuzzy Turing machines". Theor. Comput. Sci. 317: 61–69. doi:10.1016/j.tcs.2003.12.004. {{cite journal}}: Cite has empty unknown parameter: |coauthors= (help)
Yager, Ronald R. (1994). Essentials of fuzzy modeling and control. New York: Wiley. ISBN 0-471-01761-2. {{cite book}}: Unknown parameter |coauthors= ignored (|author= suggested) (help)
Van Pelt, Miles (2008). Fuzzy Logic Applied to Daily Life. Seattle, WA: No No No No Press. ISBN 0-252-16341-9.
Wilkinson, R.H. (1963). "A method of generating functions of several variables using analog diode logic". IEEE Transactions on Electronic Computers. 12: 112–129. doi:10.1109/PGEC.1963.263419. {{cite journal}}: Cite has empty unknown parameter: |coauthors= (help)
Zadeh, L.A. (1968). "Fuzzy algorithms". Information and Control. 12 (2): 94–102. doi:10.1016/S0019-9958(68)90211-8. ISSN 0019-9958. {{cite journal}}: Cite has empty unknown parameter: |coauthors= (help)
Zadeh, L.A. (1965). "Fuzzy sets". Information and Control. 8 (3): 338–353. doi:10.1016/S0019-9958(65)90241-X. ISSN 0019-9958. {{cite journal}}: Cite has empty unknown parameter: |coauthors= (help)
Zemankova-Leech, M. (1983). "Fuzzy Relational Data Bases". Ph. D. Dissertation. Florida State University. {{cite journal}}: Cite journal requires |journal= (help)
Zimmermann, H. (2001). Fuzzy set theory and its applications. Boston: Kluwer Academic Publishers. ISBN 0-7923-7435-5.

External links

Additional articles

Formal fuzzy logic - article at Citizendium
Fuzzy Logic - article at Scholarpedia
Modeling With Words - article at Scholarpedia
Fuzzy logic - article at Stanford Encyclopedia of Philosophy
Fuzzy Math - Beginner level introduction to Fuzzy Logic.
Fuzzy Logic and the Internet of Things: I-o-T

Links pages

Web page about FSQL: References and links about FSQL

Software & tools

Tutorials

Fuzzy Logic Tutorial
Another Fuzzy Logic Tutorial with MATLAB/Simulink Tutorial
Fuzzy logic in your game - tutorial aimed towards game programming.
Simple test to check how well you understand it

Applications

Research Centres

[1] Novák, V., Perfilieva, I. and Močkoř, J. (1999) Mathematical principles of fuzzy logic Dodrecht: Kluwer Academic. ISBN 0-7923-8595-0

[2] "Fuzzy Logic". Stanford Encyclopedia of Philosophy. Stanford University. 2006-07-23. Retrieved 2008-09-29.

[3] Zadeh, L.A. (1965). "Fuzzy sets", Information and Control 8 (3): 338–353.

[4] Zadeh, L. A. et al. 1996 Fuzzy Sets, Fuzzy Logic, Fuzzy Systems, World Scientific Press, ISBN 9810224214

[5] Novák, V. Are fuzzy sets a reasonable tool for modeling vague phenomena?, Fuzzy Sets and Systems 156 (2005) 341—348.

[1]

[2]

[3]

[4]

[5]

@@ Line 2: / Line 2: @@
 {{Textbook|date=January 2010}}
-{{About|the form of logic theory|the album by the Super Furry Animals|Fuzzy Logic (album)|the Powerpuff Girls episode|Fuzzy Logic (Powerpuff Girls episode)|the Grime/rock band|Fuzzy Logic (Band)}}
+{{About|the form of logic theory|the album by the Super Furry Animals|Fuzzy Logic (album)|the Powerpuff Girls episode|Fuzzy Logic (Powerpuff Girls episode)|the Grime/rock band|Fuzzy Logic (band)}}
 {{Wiktionary|fuzzy logic}}
 '''Fuzzy logic''' is a form of [[multi-valued logic]] derived from [[fuzzy set| fuzzy set theory]] to deal with [[reasoning]] that is approximate rather than precise. In contrast with "crisp logic", where [[wiktionary:binary|binary]] sets have [[binary logic]], fuzzy logic variables may have a [[truth value]] that ranges between 0 and 1 and is not constrained to the two [[truth value]]s of classic [[propositional logic]].<ref>Novák, V., Perfilieva, I. and Močkoř, J. (1999) ''Mathematical principles of fuzzy logic'' Dodrecht: Kluwer Academic. [[ISBN]] 0-7923-8595-0</ref> Furthermore, when [[linguist]]ic variables are used, these degrees may be managed by specific functions.