Refractive index

Refraction of light at the interface between two media.

The refractive index or index of refraction of a substance is a measure of the speed of light in that substance. It is expressed as a ratio of the speed of light in vacuum relative to that in the considered medium. The velocity at which light travels in vacuum is a physical constant, and the fastest speed at which energy or information can be transferred. However, light travels slower through any given material, or medium, that is not vacuum. (See: light in a medium).

A simple mathematical description of the refractive index is as follows:

n = velocity of light in a vacuum / velocity of light in medium

For example, the refractive index of water is 1.33, meaning that light travels 1.33 times faster in a vacuum as it does in water.

As light exits a medium, such as air, water, or glass, it may also change its propagation direction in proportion to the refractive index (see Snell's law). By measuring the angle of incidence and angle of refraction of the light beam, the refractive index n can be determined. Refractive index of materials varies with the frequency of radiated light. This results in a slightly different refractive index for each color. The cited values of refractive indices, such as 1.33 for water, are taken for yellow light of a sodium source which has the wavelength of 589.29 nanometers.

Definitions

The refractive index, n, of a medium is defined as the ratio of the speed, c, of a wave phenomenon such as light or sound in a reference medium to the phase speed, v_p, of the wave in the medium in question:

$n={\frac {c}{v_{\mathrm {p} }}}.$

It is most commonly used in the context of light with vacuum as a reference medium, although historically other reference media (e.g. air at a standardized pressure and temperature) have been common. It is usually given the symbol n. In the case of light, it equals

$n={\sqrt {\epsilon _{r}\mu _{r}}},$

where $\epsilon _{r}\;$ is the material's relative permittivity, and μ_r is its relative permeability. For most naturally occurring materials, μ_r is very close to 1 at optical frequencies, therefore n is approximately ${\sqrt {\epsilon _{r}}}$. Contrary to a widespread misconception, the real part of a complex n may be less than one, depending upon the material and wavelength (see dispersion (optics)). This has practical technical applications, such as effective mirrors for X-rays based on total external reflection. Another example is that the n of electromagnetic waves in plasmas is less than 1.

The phase speed is defined as the rate at which the crests of the waveform propagate; that is, the rate at which the phase of the waveform is moving. The group speed is the rate at which the envelope of the waveform is propagating; that is, the rate of variation of the amplitude of the waveform. Provided the waveform is not distorted significantly during propagation, it is the group speed that represents the rate at which information (and energy) may be transmitted by the wave (for example, the speed at which a pulse of light travels down an optical fiber). For the analytic properties constraining the unequal phase and group speeds in dispersive media, refer to dispersion (optics).

A closely related quantity is refractivity, which in atmospheric applications is denoted N and defined as N = 10⁶(n - 1). The 10⁶ factor is used because for air, n deviates from unity at most a few parts per thousand.

Speed of light

Refraction of light at the interface between two media of different refractive indices, with n₂ > n₁. Since the phase speed is lower in the second medium (v₂ < v₁), the angle of refraction θ₂ is less than the angle of incidence θ₁; that is, the ray in the higher-index medium is closer to the normal.

The speed of all electromagnetic radiation in vacuum is the same: approximately 3×10⁸ meters/second, and is denoted by c. Therefore, if v is the phase speed of radiation of a specific frequency in a specific material, the refractive index is given by

$n={\frac {c}{v}}$

or inversely

$v={\frac {c}{n}}.$

The number n is typically greater than one. However, at certain frequencies (e.g. near absorption resonances, and for X-rays), n will actually be smaller than one (see also Cherenkov radiation). This does not contradict the theory of relativity, which holds that no information-carrying signal can ever propagate faster than c, because the phase speed is not the same as the group speed or the signal speed.

Sometimes, a "group speed refractive index", usually called the group index is defined:

$n_{g}={\frac {c}{v_{g}}}$

where v_g is the group speed. This value should not be confused with n, which is always defined with respect to the phase speed. When the dispersion is small, the group velocity can be linked to the phase velocity by the relation

$v_{g}=v-\lambda {\frac {dv}{d\lambda }}.$

In this case the group index can thus be written in terms of the wavelength dependence of the refractive index as

$n_{g}={\frac {n}{1+{\frac {\lambda }{n}}{\frac {dn}{d\lambda }}}},$

where $\lambda$ is the wavelength in the medium. When the refractive index of a medium is known as a function of the vacuum wavelength (instead of the wavelength in the medium), the corresponding expression for the group index is

$n_{g}=n-\lambda _{0}{\frac {dn}{d\lambda _{0}}},$

where $\lambda _{0}$ is the wavelength in vacuum.

At the microscale, an electromagnetic wave's phase speed is slowed in a material because the electric field creates a disturbance in the charges of each atom (primarily the electrons) proportional to the permittivity of the medium. The charges will, in general, oscillate slightly out of phase with respect to the driving electric field. The charges thus radiate their own electromagnetic wave that is at the same frequency but with a phase delay. The macroscopic sum of all such contributions in the material is a wave with the same frequency but shorter wavelength than the original, leading to a slowing of the wave's phase speed. Most of the radiation from oscillating material charges will modify the incoming wave, changing its velocity. However, some net energy will be radiated in other directions (see scattering).

If in a given region the values of refractive indices n or n_g are found to differ from unity (whether homogeneously, or isotropically, or not), then this region is distinct from vacuum in the above sense for lacking Poincaré symmetry.

Interaction of light and the medium

Whereas light can be considered as particles or waves, it is treated as waves in optics. Waves travel at different speeds in different media. An example would be the difference in the speed of sound through water as opposed to its speed through air. As light crosses from one medium into another, the same wave will travel at different speeds. This process can be understood as follows: A light wave enters a transparent material and excites an electron of an atom that makes up that material. The excited electron now emits a light wave of its own, which in turn excites another electron of another atom. Between atoms, light is traveling at light speed (c = 3×10⁸ m/s). However, the time it takes to excite and emit contributes to the average time it takes for a light wave to "travel" through the medium. In glass, the apparent light speed is about 2×10⁸ m/s.

The index of refraction characterizes not only the light propagation speed, but also the bending angle and the amount of radiation transmitted and reflected by a material. It also defines the Brewster angle, the slant angle at which one polarization is totally absorbed.

The amount of light reflected from the material under normal incidence is proportional to the square of the index change at the face:

R = [(n₁-n₂)/(n₁+n₂)]²

For common glass in air, n₁ = 1 and n₂ = 1.5; thus about = 4% of light is reflected.

Negative refractive index

See also: Negative index metamaterials

Recent research has also demonstrated the existence of the negative refractive index, which can occur if permittivity and permeability have simultaneous negative values. This can be achieved with periodically constructed negative index metamaterials. The resulting negative refractive index (i.e., a reversal of Snell's law) offers the possibility of the superlens and other exotic phenomena.

Dispersion and absorption

See also: Dispersion (optics)

The variation of refractive index with wavelength for various glasses.

In real materials, the polarization does not respond instantaneously to an applied field. This causes dielectric loss, which can be expressed by a permittivity that is both complex and frequency dependent. Real materials are not perfect insulators either, i.e., they have non-zero direct current conductivity. Taking both aspects into consideration, a complex index of refraction can be defined:

${\tilde {n}}=n+i\kappa .$

Here, the real part of the refractive index n indicates the phase speed, while the imaginary part κ indicates the amount of absorption loss when the electromagnetic wave propagates through the material. (See Mathematical descriptions of opacity.) κ is often called the extinction coefficient in physics. ("Extinction coefficient" has a different definition within chemistry.) Both n and κ are dependent on the frequency (wavelength). In most circumstances $\kappa >0$ (light is absorbed) or $\kappa =0$ (light travels forever without loss). In special situations, especially lasers, it is also possible that $\kappa <0$ (light is amplified).

An alternative convention uses ${\tilde {n}}=n-i\kappa$ instead of ${\tilde {n}}=n+i\kappa$, but where $\kappa >0$ still corresponds to loss. Therefore these two conventions are inconsistent and should not be confused. The difference is related to defining sinusoidal time dependence as $\mathrm {Re} (e^{-i\omega t})$ versus $\mathrm {Re} (e^{+i\omega t})$. See Mathematical descriptions of opacity.

The effect that n varies with frequency (except in vacuum, where all frequencies travel at the same speed, c) is known as dispersion, and it is what causes a prism to divide white light into its constituent spectral colors, explains rainbows, and is the cause of chromatic aberration in lenses. In regions of the spectrum where the material does not absorb, the real part of the refractive index tends to increase with frequency. Near absorption peaks, the curve of the refractive index is a complex form given by the Kramers–Kronig relations, and can decrease with frequency.

Since the refractive index of a material varies with the frequency (and thus wavelength) of light, it is usual to specify the corresponding vacuum wavelength at which the refractive index is measured. Typically, this is done at various well-defined spectral emission lines; for example, n_D is the refractive index at the Fraunhofer "D" line, the centre of the yellow sodium double emission at 589.29 nm wavelength.

The Sellmeier equation is an empirical formula that works well in describing dispersion, and Sellmeier coefficients are often quoted instead of the refractive index in tables. For some representative refractive indices at different wavelengths, see list of indices of refraction.

As shown above, dielectric loss and non-zero DC conductivity in materials cause absorption. Good dielectric materials such as glass have extremely low DC conductivity, and at low frequencies the dielectric loss is also negligible, resulting in almost no absorption (κ ≈ 0). However, at higher frequencies (such as visible light), dielectric loss may increase absorption significantly, reducing the material's transparency to these frequencies.

The real and imaginary parts of the complex refractive index are related through use of the Kramers–Kronig relations. For example, one can determine a material's full complex refractive index as a function of wavelength from an absorption spectrum of the material.

Relation to dielectric constant

The dielectric constant (which is often dependent on wavelength) is simply the square of the (complex) refractive index in a non-magnetic medium (one with a relative permeability of unity). The refractive index is used for optics in Fresnel equations and Snell's law; while the dielectric constant is used in Maxwell's equations and electronics.

Where ${\tilde {\epsilon }}$, $\ \epsilon _{1}$, $\ \epsilon _{2}$, $n$, and $\ \kappa$ are functions of wavelength:

${\tilde {\epsilon }}=\epsilon _{1}+i\epsilon _{2}=(n+i\kappa )^{2}.$

Conversion between refractive index and dielectric constant is done by:

$\ \epsilon _{1}=n^{2}-\kappa ^{2}$

$\ \epsilon _{2}=2n\kappa$

$\ n={\sqrt {\frac {{\sqrt {\epsilon _{1}^{2}+\epsilon _{2}^{2}}}+\epsilon _{1}}{2}}}$

$\kappa ={\sqrt {\frac {{\sqrt {\epsilon _{1}^{2}+\epsilon _{2}^{2}}}-\epsilon _{1}}{2}}}.$

Anisotropy

A calcite crystal laid upon a paper with some letters showing birefringence

The refractive index of certain media may be different depending on the polarization and direction of propagation of the light through the medium. This is known as birefringence or anisotropy and is described by the field of crystal optics. In the most general case, the dielectric constant is a rank-2 tensor (a 3 by 3 matrix), which cannot simply be described by refractive indices except for polarizations along principal axes.

In magneto-optic (gyro-magnetic) and optically active materials, the principal axes are complex (corresponding to elliptical polarizations), and the dielectric tensor is complex-Hermitian (for lossless media); such materials break time-reversal symmetry and are used e.g. to construct Faraday isolators.

In crystalline calcium carbonate (calcite), the birefringent (uniaxial) optics depend on directional differences in the structure. The index of refraction also depends on composition, and can be calculated using the Gladstone–Dale relation.

Nonlinearity

The strong electric field of high intensity light (such as output of a laser) may cause a medium's refractive index to vary as the light passes through it, giving rise to nonlinear optics. If the index varies quadratically with the field (linearly with the intensity), it is called the optical Kerr effect and causes phenomena such as self-focusing and self-phase modulation. If the index varies linearly with the field (which is only possible in materials that do not possess inversion symmetry), it is known as the Pockels effect.

Inhomogeneity

A gradient-index lens with a parabolic variation of refractive index (n) with radial distance (x). The lens focuses light in the same way as a conventional lens.

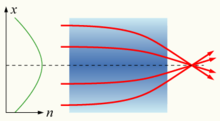
If the refractive index of a medium is not constant, but varies gradually with position, the material is known as a gradient-index medium and is described by gradient index optics. Light traveling through such a medium can be bent or focused, and this effect can be exploited to produce lenses, some optical fibers and other devices. Some common mirages are caused by a spatially-varying refractive index of air.

Relation to density

Relation between the refractive index and the density of silicate and borosilicate glasses.

In general, the refractive index of a glass increases with its density. However, there does not exist an overall linear relation between the refractive index and the density for all silicate and borosilicate glasses. A relatively high refractive index and low density can be obtained with glasses containing light metal oxides such as Li₂O and MgO, while the opposite trend is observed with glasses containing PbO and BaO as seen in the diagram at the right.

Abraham–Minkowski controversy

Main article: Abraham–Minkowski controversy

In 1908, Hermann Minkowski calculated the momentum of a refracted ray, p, where E is energy of the photon, c is the speed of light in vacuum and n is the refractive index of the medium as follows:

$p={\frac {nE}{c}}.$

In 1909, Max Abraham proposed the following formula for this calculation:

$p={\frac {E}{nc}}.$

A 2010 study suggested that both equations are correct, with the Abraham version being the kinetic momentum and the Minkowski version being the canonical momentum, and claims to explain the contradicting experimental results using this interpretation.

Applications

Wavefronts from a point source in the context of Snell's law. The region below the gray line has a higher index of refraction, and so light traveling through it has a proportionally lower phase speed than in the region above it.

The refractive index of a material is the most important property of any optical system that uses refraction. It is used to calculate the focusing power of lenses, and the dispersive power of prisms. It can also be used as a useful tool to differentiate between different types of gemstone, due to the unique chatoyance each individual stone displays.

Since refractive index is a fundamental physical property of a substance, it is often used to identify a particular substance, confirm its purity, or measure its concentration. Refractive index is used to measure solids (glasses and gemstones), liquids, and gases. Most commonly it is used to measure the concentration of a solute in an aqueous solution. A refractometer is the instrument used to measure refractive index. For a solution of sugar, the refractive index can be used to determine the sugar content (see Brix).

In GPS, the index of refraction is utilized in ray-tracing to account for the radio propagation delay due to the Earth's electrically neutral atmosphere. It is also used in Satellite link design for the Computation of radiowave attenuation in the atmosphere

See also

• List of refractive indices
• Optical properties of water and ice
• Sellmeier equation
• Total internal reflection
• Negative refractive index or Negative refraction
• Index-matching material
• Birefringence
• Calculation of glass properties
• Ellipsometry
• Metamaterial
• Negative index metamaterials
• Lorentz–Lorenz equation
• Index ellipsoid

External links

• Dielectric materials
• Negative Refractive Index
• Science World
• Filmetric's online database Free database of refractive index and absorption coefficient information
• RefractiveIndex.INFO Refractive index database featuring online plotting and parameterisation of data
• sopra-sa.com Refractive index database as text files (sign-up required)
• Simple home-made experiment which allows to determine refractive index of water
• version of the first commercial refractometer, designed by Ernst Abbe made by Carl Zeiss since 1869, here an example of 1904