User:Greek Fellows/sandbox: Difference between revisions
No edit summary |
No edit summary |
||
| Line 48: | Line 48: | ||
There are several possible stories behind this equation. A major one is that money wages are set by ''bilateral negotiations'' under partial [[bilateral monopoly]]: as the unemployment rate rises, ''all else constant'' worker bargaining power falls, so that workers are less able to increase their wages in the face of employer resistance. |
There are several possible stories behind this equation. A major one is that money wages are set by ''bilateral negotiations'' under partial [[bilateral monopoly]]: as the unemployment rate rises, ''all else constant'' worker bargaining power falls, so that workers are less able to increase their wages in the face of employer resistance. |
||
During the 1970s, this story had to be modified, because (as the late [[Abba Lerner]] had suggested in the 1940s) workers try to keep up with inflation. Since the 1970s, the equation has been changed to introduce the role of inflationary expectations (or the expected inflation rate, <math>gP^{ex}</math>). This produces the expectations-augmented wage Phillips curve: |
During the 1970s, this story had to be modified, because (as the late [[Abba Lerner]] had suggested in the 1940s) workers try to keep up with inflation. Since the 1970s, the equation has been changed to introduce the role of inflationary expectations (or the expected inflation rate, <math>gP^{\mathrm{ex}}</math>). This produces the expectations-augmented wage Phillips curve: |
||
: <math>gW = gW^T - f(U) + \lambda gP^{ex}</math> |
: <math>gW = gW^T - f(U) + \lambda \cdot gP^{\mathrm{ex}}</math> |
||
The introduction of inflationary expectations into the equation implies that actual inflation can ''feed back'' into inflationary expectations and thus cause further inflation. The late economist [[James Tobin]] dubbed the last term "inflationary inertia," because in the current period, inflation exists which represents an inflationary impulse left over from the past. |
The introduction of inflationary expectations into the equation implies that actual inflation can ''feed back'' into inflationary expectations and thus cause further inflation. The late economist [[James Tobin]] dubbed the last term "inflationary inertia," because in the current period, inflation exists which represents an inflationary impulse left over from the past. |
||
| Line 59: | Line 59: | ||
In addition, the function <math>f()</math> was modified to introduce the idea of the [[Non-Accelerating Inflation Rate of Unemployment]] (NAIRU) or what's sometimes called the "natural" rate of unemployment or the inflation-threshold unemployment rate: |
In addition, the function <math>f()</math> was modified to introduce the idea of the [[Non-Accelerating Inflation Rate of Unemployment]] (NAIRU) or what's sometimes called the "natural" rate of unemployment or the inflation-threshold unemployment rate: |
||
: <math>[1]\qquad gW = gW^T - f(U - U^*) + \lambda gP^{ex}</math> |
: <math>[1]\qquad gW = gW^T - f(U - U^*) + \lambda \cdot gP^{\mathrm{ex}}</math> |
||
Here, <math>U*</math> is the NAIRU. As discussed below, if <math>U < U^*</math>, inflation tends to accelerate. Similarly, if <math>U > U^*</math>, inflation tends to slow. It is assumed that <math>f(0) = 0</math>, so that when <math>U = U^*</math>, the <math>f</math> term drops out of the equation. |
Here, <math>U^*</math> is the NAIRU. As discussed below, if <math>U < U^*</math>, inflation tends to accelerate. Similarly, if <math>U > U^*</math>, inflation tends to slow. It is assumed that <math>f(0) = 0</math>, so that when <math>U = U^*</math>, the <math>f</math> term drops out of the equation. |
||
In equation <math>[1]</math>, the roles of <math>gW^T</math> and <math>gP^{ex}</math> seem to be redundant, playing much the same role. However, assuming that <math>\lambda</math> is equal to unity, it can be seen that they are not. If the trend rate of growth of money wages equals zero, then the case where <math>U = U^*</math> implies that <math>gW</math> equals expected inflation. That is, expected real wages are constant. |
In equation <math>[1]</math>, the roles of <math>gW^T</math> and <math>gP^{\mathrm{ex}}</math> seem to be redundant, playing much the same role. However, assuming that <math>\lambda</math> is equal to unity, it can be seen that they are not. If the trend rate of growth of money wages equals zero, then the case where <math>U = U^*</math> implies that <math>gW</math> equals expected inflation. That is, expected real wages are constant. |
||
In any reasonable economy, however, having constant expected real wages could only be consistent with actual real wages that are constant over the long haul. This does not fit with economic experience in the U.S. or any other major industrial country. Even though real wages have not risen much in recent years, there have been important increases over the decades. |
In any reasonable economy, however, having constant expected real wages could only be consistent with actual real wages that are constant over the long haul. This does not fit with economic experience in the U.S. or any other major industrial country. Even though real wages have not risen much in recent years, there have been important increases over the decades. |
||
| Line 69: | Line 69: | ||
: <math>[2]\qquad gW^T = gZ^T.</math> |
: <math>[2]\qquad gW^T = gZ^T.</math> |
||
Under assumption <math>[2]</math>, when <math>U = U*</math> and <math>\lambda</math> equals unity, expected real wages would increase with labor productivity. This would be consistent with an economy in which actual real wages increase with labor productivity. Deviations of real-wage trends from those of labor productivity might be explained by reference to other variables in the model. |
Under assumption <math>[2]</math>, when <math>U = U^*</math> and <math>\lambda</math> equals unity, expected real wages would increase with labor productivity. This would be consistent with an economy in which actual real wages increase with labor productivity. Deviations of real-wage trends from those of labor productivity might be explained by reference to other variables in the model. |
||
====Pricing decisions==== |
====Pricing decisions==== |
||
| Line 89: | Line 89: | ||
: <math>P = M \times \frac{\mathrm{average\: money\: wage}}{\mathrm{production\: labor\: productivity}} + UMC</math> |
: <math>P = M \times \frac{\mathrm{average\: money\: wage}}{\mathrm{production\: labor\: productivity}} + UMC</math> |
||
: <math>\phantom{P} = M \times W |
: <math>\phantom{P} = \frac{M \times W}{Z} + UMC</math> |
||
Now, assume that both the average price/cost mark-up (<math>M</math>) and <math>UMC</math> are constant. On the other hand, labor productivity grows, as before. Thus, an equation determining the price inflation rate (<math>gP</math>) is: |
Now, assume that both the average price/cost mark-up (<math>M</math>) and <math>UMC</math> are constant. On the other hand, labor productivity grows, as before. Thus, an equation determining the price inflation rate (<math>gP</math>) is: |
||
| Line 96: | Line 96: | ||
Then, combined with the wage Phillips curve [equation 1] and the assumption made above about the trend behavior of money wages [equation 2], this price-inflation equation gives us a simple expectations-augmented price Phillips curve: |
Then, combined with the wage Phillips curve [equation 1] and the assumption made above about the trend behavior of money wages [equation 2], this price-inflation equation gives us a simple expectations-augmented price Phillips curve: |
||
: <math>gP = -f(U - U^*) + \lambda \cdot gP^{ex}</math> |
: <math>gP = -f(U - U^*) + \lambda \cdot gP^{\mathrm{ex}}</math> |
||
Some assume that we can simply add in <math>gUMC</math>, the rate of growth of <math>UMC</math>, in order to represent the role of supply shocks (of the sort that plagued the U.S. during the 1970s). This produces a standard short-term Phillips curve: |
Some assume that we can simply add in <math>gUMC</math>, the rate of growth of <math>UMC</math>, in order to represent the role of supply shocks (of the sort that plagued the U.S. during the 1970s). This produces a standard short-term Phillips curve: |
||
: <math>gP = -f(U - U^*) + \lambda \cdot gP^{ |
: <math>gP = -f(U - U^*) + \lambda \cdot gP^{\mathrm{ex}} + gUMC</math> |
||
Economist [[Robert J. Gordon]] has called this the "Triangle Model" because it explains short-run inflationary behavior by three factors: demand inflation (due to low unemployment), supply-shock inflation (<math>gUMC</math>), and inflationary expectations or inertial inflation. |
Economist [[Robert J. Gordon]] has called this the "Triangle Model" because it explains short-run inflationary behavior by three factors: demand inflation (due to low unemployment), supply-shock inflation (<math>gUMC</math>), and inflationary expectations or inertial inflation. |
||
In the ''long run'', it is assumed, inflationary expectations catch up with and equal actual inflation so that <math>gP = gP^{ex}</math>. This represents the long-term equilibrium of expectations adjustment. Part of this adjustment may involve the adaptation of expectations to the experience with actual inflation. Another might involve guesses made by people in the economy based on other evidence. (The latter idea gave us the notion of so-called [[rational expectations]].) |
In the ''long run'', it is assumed, inflationary expectations catch up with and equal actual inflation so that <math>gP = gP^{\mathrm{ex}}</math>. This represents the long-term equilibrium of expectations adjustment. Part of this adjustment may involve the adaptation of expectations to the experience with actual inflation. Another might involve guesses made by people in the economy based on other evidence. (The latter idea gave us the notion of so-called [[rational expectations]].) |
||
Expectational equilibrium gives us the long-term Phillips curve. First, with <math>\lambda</math> less than unity: |
Expectational equilibrium gives us the long-term Phillips curve. First, with <math>\lambda</math> less than unity: |
||
| Line 112: | Line 112: | ||
This logic goes further if <math>\lambda</math> is equal to unity, i.e., if workers are able to protect their wages ''completely'' from expected inflation, even in the short run. Now, the Triangle Model equation becomes: |
This logic goes further if <math>\lambda</math> is equal to unity, i.e., if workers are able to protect their wages ''completely'' from expected inflation, even in the short run. Now, the Triangle Model equation becomes: |
||
: <math>-f(U - U^*) = gUMC<math> |
: <math>-f(U - U^*) = gUMC</math> |
||
If we further assume (as seems reasonable) that there are no long-term supply shocks, this can be simplified to become: |
If we further assume (as seems reasonable) that there are no long-term supply shocks, this can be simplified to become: |
||
: <math> |
: <math>-f(U - U^*) = 0</math> which implies that <math>U = U^*</math>. |
||
All of the assumptions imply that in the long run, there is only one possible unemployment rate, <math>U^*</math> at any one time. This uniqueness explains why some call this unemployment rate "natural." |
All of the assumptions imply that in the long run, there is only one possible unemployment rate, <math>U^*</math> at any one time. This uniqueness explains why some call this unemployment rate "natural." |
||
| Line 125: | Line 125: | ||
Start with the [[aggregate supply]] function: |
Start with the [[aggregate supply]] function: |
||
:<math>Y = Y_n + a (P-P_e) |
:<math>Y = Y_n + a (P - P_e)</math> |
||
where <math>Y</math> is log value of the actual [[output (economics)|output]], <math>Y_n</math> is log value of the "natural" level of output, <math>a</math> is a positive constant, <math>P</math> is log value of the actual [[price level]], and <math>P_e</math> is log value of the expected [[price level]]. Lucas assumes that <math>Y_n</math> has a unique value. |
where <math>Y</math> is log value of the actual [[output (economics)|output]], <math>Y_n</math> is log value of the "natural" level of output, <math>a</math> is a positive constant, <math>P</math> is log value of the actual [[price level]], and <math>P_e</math> is log value of the expected [[price level]]. Lucas assumes that <math>Y_n</math> has a unique value. |
||
| Line 134: | Line 134: | ||
We re-arrange the equation into: |
We re-arrange the equation into: |
||
: <math>P = P_e + \frac{Y - Y_n}{a} |
: <math>P = P_e + \frac{Y - Y_n}{a}</math> |
||
Next we add unexpected exogenous shocks to the world supply |
Next we add unexpected exogenous shocks to the world supply <math>v</math>: |
||
: <math>P = P_e + \frac{Y - Y_n}{a} + v |
: <math>P = P_e + \frac{Y - Y_n}{a} + v</math> |
||
Subtracting last year's price levels |
Subtracting last year's price levels <math>P_{-1}</math> will give us inflation rates, because |
||
: <math>P - P_{-1}\ \approx \pi </math> |
: <math>P - P_{-1}\ \approx \pi </math> |
||
| Line 151: | Line 151: | ||
where <math>b</math> is a positive constant, <math>U</math> is unemployment, and <math>U_n</math> is the [[natural rate of unemployment]] or [[NAIRU]], we arrive at the final form of the short-run Phillips curve: |
where <math>b</math> is a positive constant, <math>U</math> is unemployment, and <math>U_n</math> is the [[natural rate of unemployment]] or [[NAIRU]], we arrive at the final form of the short-run Phillips curve: |
||
: <math>\pi = \pi_e - b(U - U_n) + v |
: <math>\pi = \pi_e - b(U - U_n) + v</math> |
||
This equation, plotting inflation rate <math>\pi</math> against unemployment <math>U</math> gives the downward-sloping curve in the diagram that characterises the Phillips curve. |
This equation, plotting inflation rate <math>\pi</math> against unemployment <math>U</math> gives the downward-sloping curve in the diagram that characterises the Phillips curve. |
||
Revision as of 12:33, 22 December 2014
This article needs additional citations for verification. (October 2011) |
In economics, the Phillips curve is a historical inverse relationship between rates of unemployment and corresponding rates of inflation that result in an economy. Stated simply, decreased unemployment, (i.e., increased levels of employment) in an economy will correlate with higher rates of inflation.
While there is a short run tradeoff between unemployment and inflation, it has not been observed in the long run.[1] In 1968, Milton Friedman asserted that the Phillips Curve was only applicable in the short-run and that in the long-run, inflationary policies will not decrease unemployment.[2] Friedman then correctly predicted that, in the upcoming years after 1968, both inflation and unemployment would increase.[2] The long-run Phillips Curve is now seen as a vertical line at the natural rate of unemployment, where the rate of inflation has no effect on unemployment. [3] Accordingly, the Phillips curve is now seen as too simplistic, with the unemployment rate supplanted by more accurate predictors of inflation based on velocity of money supply measures such as the MZM ("money zero maturity") velocity,[4] which is affected by unemployment in the short but not the long term.[5]
History
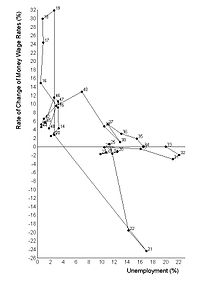
William Phillips, a New Zealand born economist, wrote a paper in 1958 titled The Relation between Unemployment and the Rate of Change of Money Wage Rates in the United Kingdom, 1861-1957, which was published in the quarterly journal Economica. In the paper Phillips describes how he observed an inverse relationship between money wage changes and unemployment in the British economy over the period examined. Similar patterns were found in other countries and in 1960 Paul Samuelson and Robert Solow took Phillips' work and made explicit the link between inflation and unemployment: when inflation was high, unemployment was low, and vice-versa.
In the 1920s an American economist Irving Fisher noted this kind of Phillips curve relationship. However, Phillips' original curve described the behavior of money wages.[6]
In the years following Phillips' 1958 paper, many economists in the advanced industrial countries believed that his results showed that there was a permanently stable relationship between inflation and unemployment.[citation needed] One implication of this for government policy was that governments could control unemployment and inflation with a Keynesian policy. They could tolerate a reasonably high rate of inflation as this would lead to lower unemployment – there would be a trade-off between inflation and unemployment. For example, monetary policy and/or fiscal policy (i.e., deficit spending) could be used to stimulate the economy, raising gross domestic product and lowering the unemployment rate. Moving along the Phillips curve, this would lead to a higher inflation rate, the cost of enjoying lower unemployment rates.[citation needed] Economist James Forder argues that this view is historically false and that neither economists nor governments took that view and that the 'Phillips curve myth' was an invention of the 1970s.[7]
Since 1974 seven Nobel Prizes have been given for work critical of the Phillips curve. Some of this criticism is based on the United States' experience during the 1970s, which had periods of high unemployment and high inflation at the same time. The authors receiving those prizes include Thomas Sargent, Christopher Sims, Edmund Phelps, Edward Prescott, Robert A. Mundell, Robert E. Lucas, Milton Friedman, and F.A. Hayek.[8]
Stagflation
In the 1970s, many countries experienced high levels of both inflation and unemployment also known as stagflation. Theories based on the Phillips curve suggested that this could not happen, and the curve came under a concerted attack from a group of economists headed by Milton Friedman.[citation needed] Friedman argued that the Phillips curve relationship was only a short-run phenomenon. In this he followed 8 years after Samuelson and Solow [1960] who wrote " All of our discussion has been phrased in short-run terms, dealing with what might happen in the next few years. It would be wrong, though, to think that our Figure 2 menu that related obtainable price and unemployment behavior will maintain its same shape in the longer run. What we do in a policy way during the next few years might cause it to shift in a definite way. "[9] As Samuelson and Solow had argued 8 years earlier, he argued that in the long run, workers and employers will take inflation into account, resulting in employment contracts that increase pay at rates near anticipated inflation. Unemployment would then begin to rise back to its previous level, but now with higher inflation rates. This result implies that over the longer-run there is no trade-off between inflation and unemployment. This implication is significant for practical reasons because it implies that central banks should not set employment targets above the natural rate.[1]
More recent research has shown that there is a moderate trade-off between low-levels of inflation and unemployment. Work by George Akerlof, William Dickens, and George Perry,[10] implies that if inflation is reduced from two to zero percent, unemployment will be permanently increased by 1.5 percent. This is because workers generally have a higher tolerance for real wage cuts than nominal ones. For example, a worker will more likely accept a wage increase of two percent when inflation is three percent, than a wage cut of one percent when the inflation rate is zero.
The Phillips curve today

Most economists no longer use the Phillips curve in its original form because it was shown to be too simplistic.[5] This can be seen in a cursory analysis of US inflation and unemployment data from 1953-92. There is no single curve that will fit the data, but there are three rough aggregations—1955–71, 1974–84, and 1985–92—each of which shows a general, downwards slope, but at three very different levels with the shifts occurring abruptly. The data for 1953-54 and 1972-73 do not group easily, and a more formal analysis posits up to five groups/curves over the period.[1]
But still today, modified forms of the Phillips Curve that take inflationary expectations into account remain influential. The theory goes under several names, with some variation in its details, but all modern versions distinguish between short-run and long-run effects on unemployment. The "short-run Phillips curve" is also called the "expectations-augmented Phillips curve", since it shifts up when inflationary expectations rise, Edmund Phelps and Milton Friedman argued. In the long run, this implies that monetary policy cannot affect unemployment, which adjusts back to its "natural rate", also called the "NAIRU" or "long-run Phillips curve". However, this long-run "neutrality" of monetary policy does allow for short run fluctuations and the ability of the monetary authority to temporarily decrease unemployment by increasing permanent inflation, and vice versa. Blanchard (2000, chapter 8) gives a textbook presentation of the expectations-augmented Phillips curve.
An equation like the expectations-augmented Phillips curve also appears in many recent New Keynesian dynamic stochastic general equilibrium models. In these macroeconomic models with sticky prices, there is a positive relation between the rate of inflation and the level of demand, and therefore a negative relation between the rate of inflation and the rate of unemployment. This relationship is often called the "New Keynesian Phillips curve." Like the expectations-augmented Phillips curve, the New Keynesian Phillips curve implies that increased inflation can lower unemployment temporarily, but cannot lower it permanently. Two influential papers that incorporate a New Keynesian Phillips curve are Clarida, Galí, and Gertler (1999) and Blanchard and Galí (2007).
Mathematics and the Phillips curve
There are at least two different mathematical derivations of the Phillips curve. First, there is the traditional or Keynesian version. Then, there is the new Classical version associated with Robert E. Lucas, Jr.
The traditional Phillips curve
The original Phillips curve literature was not based on the unaided application of economic theory. Instead, it was based on empirical generalizations. After that, economists tried to develop theories that fit the data.
Money wage determination
The traditional Phillips curve story starts with a wage Phillips Curve, of the sort described by A.W. Phillips himself. This describes the rate of growth of money wages (). Here and below, the operator is the equivalent of "the percentage rate of growth of" the variable that follows.
The "money wage rate" () is shorthand for total money wage costs per production employee, including benefits and payroll taxes. The focus is on only production workers' money wages, because (as discussed below) these costs are crucial to pricing decisions by the firms.
This equation tells us that the growth of money wages rises with the trend rate of growth of money wages (indicated by the superscript ) and falls with the unemployment rate (). The function is assumed to be monotonically increasing with so that the dampening of money-wage increases by unemployment is shown by the negative sign in the equation above.
There are several possible stories behind this equation. A major one is that money wages are set by bilateral negotiations under partial bilateral monopoly: as the unemployment rate rises, all else constant worker bargaining power falls, so that workers are less able to increase their wages in the face of employer resistance.
During the 1970s, this story had to be modified, because (as the late Abba Lerner had suggested in the 1940s) workers try to keep up with inflation. Since the 1970s, the equation has been changed to introduce the role of inflationary expectations (or the expected inflation rate, ). This produces the expectations-augmented wage Phillips curve:
The introduction of inflationary expectations into the equation implies that actual inflation can feed back into inflationary expectations and thus cause further inflation. The late economist James Tobin dubbed the last term "inflationary inertia," because in the current period, inflation exists which represents an inflationary impulse left over from the past.
It also involved much more than expectations, including the price-wage spiral. In this spiral, employers try to protect profits by raising their prices and employees try to keep up with inflation to protect their real wages. This process can feed on itself, becoming a self-fulfilling prophecy.
The parameter (which is presumed constant during any time period) represents the degree to which employees can gain money wage increases to keep up with expected inflation, preventing a fall in expected real wages. It is usually assumed that this parameter equals unity in the long run.
In addition, the function was modified to introduce the idea of the Non-Accelerating Inflation Rate of Unemployment (NAIRU) or what's sometimes called the "natural" rate of unemployment or the inflation-threshold unemployment rate:
Here, is the NAIRU. As discussed below, if , inflation tends to accelerate. Similarly, if , inflation tends to slow. It is assumed that , so that when , the term drops out of the equation.
In equation , the roles of and seem to be redundant, playing much the same role. However, assuming that is equal to unity, it can be seen that they are not. If the trend rate of growth of money wages equals zero, then the case where implies that equals expected inflation. That is, expected real wages are constant.
In any reasonable economy, however, having constant expected real wages could only be consistent with actual real wages that are constant over the long haul. This does not fit with economic experience in the U.S. or any other major industrial country. Even though real wages have not risen much in recent years, there have been important increases over the decades.
An alternative is to assume that the trend rate of growth of money wages equals the trend rate of growth of average labor productivity (). That is:
Under assumption , when and equals unity, expected real wages would increase with labor productivity. This would be consistent with an economy in which actual real wages increase with labor productivity. Deviations of real-wage trends from those of labor productivity might be explained by reference to other variables in the model.
Pricing decisions
Next, there is price behavior. The standard assumption is that markets are imperfectly competitive, where most businesses have some power to set prices. So the model assumes that the average business sets prices as a mark-up () over unit labor costs in production measured at a standard rate of capacity utilization (say, at 90 percent use of plant and equipment) and then add in unit material costs.
The standardization involves later ignoring deviations from the trend in labor productivity. For example, assume that the growth of labor productivity is the same as that in the trend and that current productivity equals its trend value:
- and
The markup reflects both the firm's degree of market power and the extent to which overhead costs have to be paid. Put another way, all else equal, rises with the firm's power to set prices or with a rise of overhead costs relative to total costs.
So pricing follows this equation:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:6011/en.wikipedia.org/v1/":): {\displaystyle P = M \times \mathrm{unit\: labor\: costs} + \mathrm{unit\: materials\: cost}}
- Failed to parse (syntax error): {\displaystyle \phantom{P} = M \times \frac{\mathrm{total\: production\: employment\: cost}}{\mathrm{quantity\: of\: output}} + UMC}
is unit raw materials cost (total raw materials costs divided by total output). So the equation can be restated as:
- Failed to parse (syntax error): {\displaystyle P = M \times \frac{\mathrm{production\: employment\: cost\: per\: worker}}{\mathrm{output\: per\: production\: employee}} + UMC}
This equation can again be stated as:
- Failed to parse (syntax error): {\displaystyle P = M \times \frac{\mathrm{average\: money\: wage}}{\mathrm{production\: labor\: productivity}} + UMC}
Now, assume that both the average price/cost mark-up () and are constant. On the other hand, labor productivity grows, as before. Thus, an equation determining the price inflation rate () is:
The price Phillips curves
Then, combined with the wage Phillips curve [equation 1] and the assumption made above about the trend behavior of money wages [equation 2], this price-inflation equation gives us a simple expectations-augmented price Phillips curve:
Some assume that we can simply add in , the rate of growth of , in order to represent the role of supply shocks (of the sort that plagued the U.S. during the 1970s). This produces a standard short-term Phillips curve:
Economist Robert J. Gordon has called this the "Triangle Model" because it explains short-run inflationary behavior by three factors: demand inflation (due to low unemployment), supply-shock inflation (), and inflationary expectations or inertial inflation.
In the long run, it is assumed, inflationary expectations catch up with and equal actual inflation so that . This represents the long-term equilibrium of expectations adjustment. Part of this adjustment may involve the adaptation of expectations to the experience with actual inflation. Another might involve guesses made by people in the economy based on other evidence. (The latter idea gave us the notion of so-called rational expectations.)
Expectational equilibrium gives us the long-term Phillips curve. First, with less than unity:
This is nothing but a steeper version of the short-run Phillips curve above. Inflation rises as unemployment falls, while this connection is stronger. That is, a low unemployment rate (less than ) will be associated with a higher inflation rate in the long run than in the short run. This occurs because the actual higher-inflation situation seen in the short run feeds back to raise inflationary expectations, which in turn raises the inflation rate further. Similarly, at high unemployment rates (greater than ) lead to low inflation rates. These in turn encourage lower inflationary expectations, so that inflation itself drops again.
This logic goes further if is equal to unity, i.e., if workers are able to protect their wages completely from expected inflation, even in the short run. Now, the Triangle Model equation becomes:
If we further assume (as seems reasonable) that there are no long-term supply shocks, this can be simplified to become:
- which implies that .
All of the assumptions imply that in the long run, there is only one possible unemployment rate, at any one time. This uniqueness explains why some call this unemployment rate "natural."
To truly understand and criticize the uniqueness of , a more sophisticated and realistic model is needed. For example, we might introduce the idea that workers in different sectors push for money wage increases that are similar to those in other sectors. Or we might make the model even more realistic. One important place to look is at the determination of the mark-up, .
New classical version
The Phillips curve equation can be derived from the (short-run) Lucas aggregate supply function. The Lucas approach is very different from that the traditional view. Instead of starting with empirical data, he started with a classical economic model following very simple economic principles.
Start with the aggregate supply function:
where is log value of the actual output, is log value of the "natural" level of output, is a positive constant, is log value of the actual price level, and is log value of the expected price level. Lucas assumes that has a unique value.
Note that this equation indicates that when expectations of future inflation (or, more correctly, the future price level) are totally accurate, the last term drops out, so that actual output equals the so-called "natural" level of real GDP. This means that in the Lucas aggregate supply curve, the only reason why actual real GDP should deviate from potential—and the actual unemployment rate should deviate from the "natural" rate—is because of incorrect expectations of what is going to happen with prices in the future. (The idea has been expressed first by Keynes, "General Theory," Chapter 20 section III paragraph 4).
This differs from other views of the Phillips curve, in which the failure to attain the "natural" level of output can be due to the imperfection or incompleteness of markets, the stickiness of prices, and the like. In the non-Lucas view, incorrect expectations can contribute to aggregate demand failure, but they are not the only cause. To the "new Classical" followers of Lucas, markets are presumed to be perfect and always attain equilibrium (given inflationary expectations).
We re-arrange the equation into:
Next we add unexpected exogenous shocks to the world supply :
Subtracting last year's price levels will give us inflation rates, because
and
where and are the inflation and expected inflation respectively.
There is also a negative relationship between output and unemployment (as expressed by Okun's law). Therefore using
where is a positive constant, is unemployment, and is the natural rate of unemployment or NAIRU, we arrive at the final form of the short-run Phillips curve:
This equation, plotting inflation rate against unemployment gives the downward-sloping curve in the diagram that characterises the Phillips curve.
New Keynesian version
The New Keynesian Phillips curve was originally derived by Roberts in 1995,[11] and since been used in most state-of-the-art New Keynesian DSGE models like the one of Clarida, Galí, and Gertler (2000).[12][13]
where . The current expectations of next period's inflation are incorporated as
NAIRU and rational expectations

In the 1970s, new theories, such as rational expectations and the NAIRU (non-accelerating inflation rate of unemployment) arose to explain how stagflation could occur. The latter theory, also known as the "natural rate of unemployment", distinguished between the "short-term" Phillips curve and the "long-term" one. The short-term Phillips Curve looked like a normal Phillips Curve, but shifted in the long run as expectations changed. In the long run, only a single rate of unemployment (the NAIRU or "natural" rate) was consistent with a stable inflation rate. The long-run Phillips Curve was thus vertical, so there was no trade-off between inflation and unemployment. Edmund Phelps won the Nobel Prize in Economics in 2006 in part for this. However, the expectations argument was in fact very widely understood before his work on it.[14]
In the diagram, the long-run Phillips curve is the vertical red line. The NAIRU theory says that when unemployment is at the rate defined by this line, inflation will be stable. However, in the short-run policymakers will face an inflation-unemployment rate tradeoff marked by the "Initial Short-Run Phillips Curve" in the graph. Policymakers can therefore reduce the unemployment rate temporarily, moving from point A to point B through expansionary policy. However, according to the NAIRU, exploiting this short-run tradeoff will raise inflation expectations, shifting the short-run curve rightward to the "New Short-Run Phillips Curve" and moving the point of equilibrium from B to C. Thus the reduction in unemployment below the "Natural Rate" will be temporary, and lead only to higher inflation in the long run.
Since the short-run curve shifts outward due to the attempt to reduce unemployment, the expansionary policy ultimately worsens the exploitable tradeoff between unemployment and inflation. That is, it results in more inflation at each short-run unemployment rate. The name "NAIRU" arises because with actual unemployment below it, inflation accelerates, while with unemployment above it, inflation decelerates. With the actual rate equal to it, inflation is stable, neither accelerating nor decelerating. One practical use of this model was to provide an explanation for stagflation, which confounded the traditional Phillips curve.
The rational expectations theory said that expectations of inflation were equal to what actually happened, with some minor and temporary errors. This in turn suggested that the short-run period was so short that it was non-existent: any effort to reduce unemployment below the NAIRU, for example, would immediately cause inflationary expectations to rise and thus imply that the policy would fail. Unemployment would never deviate from the NAIRU except due to random and transitory mistakes in developing expectations about future inflation rates. In this perspective, any deviation of the actual unemployment rate from the NAIRU was an illusion.
However, in the 1990s in the U.S., it became increasingly clear that the NAIRU did not have a unique equilibrium and could change in unpredictable ways. In the late 1990s, the actual unemployment rate fell below 4% of the labor force, much lower than almost all estimates of the NAIRU. But inflation stayed very moderate rather than accelerating. So, just as the Phillips curve had become a subject of debate, so did the NAIRU.
Furthermore, the concept of rational expectations had become subject to much doubt when it became clear that the main assumption of models based on it was that there exists a single (unique) equilibrium in the economy that is set ahead of time, determined independently of demand conditions. The experience of the 1990s suggests that this assumption cannot be sustained.
Theoretical questions
The Phillips curve started as an empirical observation in search of a theoretical explanation. Specifically, the Phillips curve tried to determine whether the inflation-unemployment link was causal or simply correlational. There are several major explanations of the short-term Phillips Curve regularity.
To Milton Friedman there is a short-term correlation between inflation shocks and employment. When an inflationary surprise occurs, workers are fooled into accepting lower pay because they do not see the fall in real wages right away. Firms hire them because they see the inflation as allowing higher profits for given nominal wages. This is a movement along the Phillips curve as with change A. Eventually, workers discover that real wages have fallen, so they push for higher money wages. This causes the Phillips curve to shift upward and to the right, as with B.
Economists such as Milton Friedman and Edmund Phelps reject this theory because it implies that workers suffer from money illusion. According to them, rational workers would only react to real wages, that is, inflation adjusted wages. However, one of the characteristics of a modern industrial economy is that workers do not encounter their employers in an atomized and perfect market. They operate in a complex combination of imperfect markets, monopolies, monopsonies, labor unions, and other institutions. In many cases, they may lack the bargaining power to act on their expectations, no matter how rational they are, or their perceptions, no matter how free of money illusion they are. It is not that high inflation causes low unemployment (as in Milton Friedman's theory) as much as vice-versa: Low unemployment raises worker bargaining power, allowing them to successfully push for higher nominal wages. To protect profits, employers raise prices.
Similarly, built-in inflation is not simply a matter of subjective "inflationary expectations" but also reflects the fact that high inflation can gather momentum and continue beyond the time when it was started, due to the objective price/wage spiral.
However, other economists, like Jeffrey Herbener, argue that price is market-determined and competitive firms cannot simply raise prices.[citation needed] They reject the Phillips curve entirely, concluding that unemployment's influence is only a small portion of a much larger inflation picture that includes prices of raw materials, intermediate goods, cost of raising capital, worker productivity, land, and other factors.
Gordon's triangle model
Robert J. Gordon of Northwestern University has analyzed the Phillips curve to produce what he calls the triangle model, in which the actual inflation rate is determined by the sum of
- demand pull or short-term Phillips curve inflation,
- cost push or supply shocks, and
- built-in inflation.
The last reflects inflationary expectations and the price/wage spiral. Supply shocks and changes in built-in inflation are the main factors shifting the short-run Phillips Curve and changing the trade-off. In this theory, it is not only inflationary expectations that can cause stagflation. For example, the steep climb of oil prices during the 1970s could have this result.
Changes in built-in inflation follow the partial-adjustment logic behind most theories of the NAIRU:
- Low unemployment encourages high inflation, as with the simple Phillips curve. But if unemployment stays low and inflation stays high for a long time, as in the late 1960s in the U.S., both inflationary expectations and the price/wage spiral accelerate. This shifts the short-run Phillips curve upward and rightward, so that more inflation is seen at any given unemployment rate. (This is with shift B in the diagram.)
- High unemployment encourages low inflation, again as with a simple Phillips curve. But if unemployment stays high and inflation stays low for a long time, as in the early 1980s in the U.S., both inflationary expectations and the price/wage spiral slow. This shifts the short-run Phillips curve downward and leftward, so that less inflation is seen at each unemployment rate.
In between these two lies the NAIRU, where the Phillips curve does not have any inherent tendency to shift, so that the inflation rate is stable. However, there seems to be a range in the middle between "high" and "low" where built-in inflation stays stable. The ends of this "non-accelerating inflation range of unemployment rates" change over time.
See also
Notes
- ^ a b c Chang, R. (1997) "Is Low Unemployment Inflationary?" Federal Reserve Bank of Atlanta Economic Review 1Q97:4-13
- ^ a b Phelan, John (23 October 2012). "Milton Friedman and the rise and fall of the Phillips Curve". thecommentator.com. Retrieved September 29, 2014.
- ^ http://www.econlib.org/library/Enc/PhillipsCurve.html#lfHendersonCEE2-126_figure_036
- ^ MZM velocity
- ^ a b Oliver Hossfeld (2010) "US Money Demand, Monetary Overhang, and Inflation Prediction" International Network for Economic Research working paper no. 2010.4
- ^ I Discovered the Phillips Curve: "A Statistical Relation between Unemployment and Price Changes" Irving Fisher. The Journal of Political Economy, Vol. 81, No. 2, Part 1 (Mar. - Apr., 1973), pp. 496-502. Reprint of 1926 article by Irving Fisher.
- ^ Forder, James (2014). Macroeconomics and the Phillips curve myth. Oxford University Press.
- ^ Domitrovic, Brain (10 October 2011). "The Economics Nobel Goes to Sargent & Sims: Attackers of the Phillips Curve". Forbes.com. Retrieved 12 October 2011.
- ^ "Analytical Aspects of Anti-Inflation Policy" Paul H. Samuelson; Robert M. Solow American Economic Reivew Vol. 50, No. 2, Papers and Procedings of the Seventy-second Annual Meeting of the American Economic Association (May, 1960), 177-194.
- ^ George A. Akerlof, William T. Dickens, and George L. Perry, "Near-Rational Wage and Price Setting and the Long-Run Phillips Curve," Brookings Papers on Economic Activity , Vol. 2000, No. 1 (2000), pp. 1-60
- ^ Roberts, John M. (1995). "New Keynesian Economics and the Phillips Curve". Journal of Money, Credit and Banking. 27 (4): 975–984. JSTOR 2077783.
- ^ Clarida, Richard; Galí, Jordi; Gertler, Mark (2000). "Monetary Policy Rules and Macroeconomic Stability: Evidence and Some Theory". The Quarterly Journal of Economics. 115 (1): 147–180. doi:10.1162/003355300554692.
- ^ Romer, David (2012). "Dynamic Stochastic General Equilibrium Models of Fluctuation". Advanced Macroeconomics. New York: McGraw-Hill Irwin. pp. 312–364. ISBN 978-0-07-351137-5.
- ^ Forder, James (2010). "The historical place of the 'Friedman-Phelps' expectations critique". European Journal of the History of Economic Thought. 17 (3): 493-511.
References
- Blanchard, Olivier (2000). Macroeconomics (Second ed.). Prentice Hall. ISBN 0-13-013306-X.
- Blanchard, Olivier; Galí, Jordi (2007). "Real Wage Rigidities and the New Keynesian Model". Journal of Money, Credit, and Banking. 39 (s1): 35–65. doi:10.1111/j.1538-4616.2007.00015.x.
- Clarida, Richard; Galí, Jordi; Gertler, Mark (1999). "The science of monetary policy: a New-Keynesian perspective". Journal of Economic Literature. 37 (4). American Economic Association: 1661–1707. doi:10.1257/jel.37.4.1661. JSTOR 2565488.
- Fisher, Irving (1973). "I discovered the Phillips curve: 'A statistical relation between unemployment and price changes'". Journal of Political Economy. 81 (2). The University of Chicago Press: 496–502. doi:10.1086/260048. JSTOR 1830534. Reprinted from 1926 edition of International Labour Review.
- Friedman, Milton (1968). "The role of monetary policy". American Economic Review. 68 (1): 1–17. JSTOR 1831652.
- Keynes, John Maynard (1936) The General Theory of Employment, Interest and Money
- Phillips, A. W. (1958). "The Relationship between Unemployment and the Rate of Change of Money Wages in the United Kingdom 1861-1957". Economica. 25 (100): 283–299. doi:10.1111/j.1468-0335.1958.tb00003.x.
- Salsman, Richard M. (1997). "The Cross and the Curve". The Intellectual Activist. 11 (3): 9–20. ISSN 0730-2355.
Further reading
- Federal Reserve Bank of Boston, "Understanding Inflation and the Implications for Monetary Policy: A Phillips Curve Retrospective", FRBB Conference Series 53, June 9–11, 2008, Chatham, Massachusetts.
- Gordon, Robert J. (2011). "The History of the Phillips Curve: Consensus and Bifurcation". Economica. 78 (309): 10–50. doi:10.1111/j.1468-0335.2009.00815.x.
- Hoover, Kevin D. (2008). "Phillips Curve". In David R. Henderson (ed.) (ed.). Concise Encyclopedia of Economics (2nd ed.). Indianapolis: Library of Economics and Liberty. ISBN 978-0865976658. OCLC 237794267.
{{cite encyclopedia}}:|editor=has generic name (help) - Qin, Duo (2011). "The Phillips Curve from the Perspective of the History of Econometrics". History of Political Economy. 43 (Suppl. 1): 283–308. doi:10.1215/00182702-1158763.
External links
- Left critique of Phillips Curve from Dollars & Sense magazine
- A Critique of the Phillips Curve by Charles Oliver, Ludwig von Mises Institute, February 9, 1999 (includes the article "Who's Afraid Of A Red-Hot Economy?", Investor's Business Daily, February 9, 1999)
- Audio speech by Jeffery Herbener at the Ludwig Von Mises Institute.












![{\displaystyle [1]\qquad gW=gW^{T}-f(U-U^{*})+\lambda \cdot gP^{\mathrm {ex} }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d406b4473d2a2de6b2bf5957b320df0d5fc40197)






![{\displaystyle [1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/83021ecdd7307a04dbb7873affcaac031e7e935a)


![{\displaystyle [2]\qquad gW^{T}=gZ^{T}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3e86bb3e393f9b3606cd43df49fc3422d26f1db)
![{\displaystyle [2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa32363c093f4cfd50ecba68068bcfd396ea8bff)
































![{\displaystyle \pi _{t}=\beta E_{t}[\pi _{t+1}]+\kappa y_{t}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ef7dd57c38352c58215d6a0a3e102a4218956f6)
![{\displaystyle \kappa ={\frac {\alpha [1-(1-\alpha )\beta ]\phi }{1-\alpha }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/72581a708ec3cd91521edd09339480edf729cf7d)
![{\displaystyle \beta E_{t}[\pi _{t+1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/665311ff5571a987a4e48a2435270b77aa595d37)