Jump to content

Capsid: Difference between revisions

From Wikipedia, the free encyclopedia
Browse history interactively
← Previous editNext edit →
Content deleted Content added
VisualWikitext
Dexbot (talk | contribs)
Bots
192,481 edits
m Removing Link GA template (handled by wikidata)
Sxoa (talk | contribs)
163 edits
→Helical: I citation needed as opposed to failed verification as the article linked to has nothing to with influenza or even viruses.
Line 25: Line 25:
===Helical===
===Helical===
[[Image:Helical capsid.jpg|thumb|left|3D model of Helical capsid structure]]
[[Image:Helical capsid.jpg|thumb|left|3D model of Helical capsid structure]]
Many rod-shaped and filamentous plant viruses have capsids with helical symmetry.<ref>{{cite journal |author=Yamada S, Matsuzawa T, Yamada K, Yoshioka S, Ono S, Hishinuma T |title=Modified inversion recovery method for nuclear magnetic resonance imaging |journal=Sci Rep Res Inst Tohoku Univ Med |volume=33 |issue=1-4 |pages=9–15 |date=December 1986 |pmid=3629216 |doi= |url=}}</ref> The helical structure can be described as a set of n 1-D molecular helices related by an n-fold axial symmetry.<ref> {{cite journal |author=Aldrich RA |title=Children in cities--Seattle's KidsPlace program |journal=Acta Paediatr Jpn |volume=29 |issue=1 |pages=84–90 |date=February 1987 |pmid=3144854 |doi= |url=}}</ref> The helical transformation are classified into two categories: one-dimensional and two-dimensional helical systems.<ref>{{cite journal |author=Aldrich RA |title=Children in cities--Seattle's KidsPlace program |journal=Acta Paediatr Jpn |volume=29 |issue=1 |pages=84–90 |date=February 1987 |pmid=3144854 |doi= |url=}}</ref> Creating an entire helical structure relies on a set of translational and rotational matrices which are coded in the protein data bank.<ref>{{cite journal |author=Aldrich RA |title=Children in cities--Seattle's KidsPlace program |journal=Acta Paediatr Jpn |volume=29 |issue=1 |pages=84–90 |date=February 1987 |pmid=3144854 |doi= |url=}}</ref> Helical symmetry is given by the formula P=μ x ρ, where μ is the number of structural units per turn of the helix, ρ is the axial rise per unit and P is the pitch of the helix. The structure is said to be open due to the characteristic that any volume can be enclosed by varying the length of the helix.<ref name="virology">{{cite book |author=Racaniello, Vincent R.; Enquist, L. W. |title=Principles of Virology, Vol. 1: Molecular Biology |publisher=ASM Press |location=Washington, D.C |year=2008 |pages= |isbn=1-55581-479-4 |oclc= |doi= |accessdate=}}</ref> The most understood helical virus is the tobacco mosaic virus.<ref>{{cite journal |author=Yamada S, Matsuzawa T, Yamada K, Yoshioka S, Ono S, Hishinuma T |title=Modified inversion recovery method for nuclear magnetic resonance imaging |journal=Sci Rep Res Inst Tohoku Univ Med |volume=33 |issue=1-4 |pages=9–15 |date=December 1986 |pmid=3629216 |doi= |url=}}</ref>The virus is a single molecule of (+) strand RNA. Each coat protein on the interior of the helix bind three nucleotides of the RNA genome. Influenza A viruses differ by comprising multiple ribonucleoproteins, the viral NP protein organizes the RNA into a helical structure. The size is also different the tobacco mosaic virus has a 16.33 protein subunits per helical turn,<ref>{{cite journal |author=Yamada S, Matsuzawa T, Yamada K, Yoshioka S, Ono S, Hishinuma T |title=Modified inversion recovery method for nuclear magnetic resonance imaging |journal=Sci Rep Res Inst Tohoku Univ Med |volume=33 |issue=1-4 |pages=9–15 |date=December 1986 |pmid=3629216 |doi= |url=}}</ref> while the influenza A virus has a 28 amino acid tail loop.<ref>{{cite journal |author=Mitchell T, Sariban E, Kufe D |title=Effects of 1-beta-D-arabinofuranosylcytosine on proto-oncogene expression in human U-937 cells |journal=Mol. Pharmacol. |volume=30 |issue=4 |pages=398–402 |date=October 1986 |pmid=3531806 |doi= |url=}}</ref>
Many rod-shaped and filamentous plant viruses have capsids with helical symmetry.<ref>{{cite journal |author=Yamada S, Matsuzawa T, Yamada K, Yoshioka S, Ono S, Hishinuma T |title=Modified inversion recovery method for nuclear magnetic resonance imaging |journal=Sci Rep Res Inst Tohoku Univ Med |volume=33 |issue=1-4 |pages=9–15 |date=December 1986 |pmid=3629216 |doi= |url=}}</ref> The helical structure can be described as a set of n 1-D molecular helices related by an n-fold axial symmetry.<ref> {{cite journal |author=Aldrich RA |title=Children in cities--Seattle's KidsPlace program |journal=Acta Paediatr Jpn |volume=29 |issue=1 |pages=84–90 |date=February 1987 |pmid=3144854 |doi= |url=}}</ref> The helical transformation are classified into two categories: one-dimensional and two-dimensional helical systems.<ref>{{cite journal |author=Aldrich RA |title=Children in cities--Seattle's KidsPlace program |journal=Acta Paediatr Jpn |volume=29 |issue=1 |pages=84–90 |date=February 1987 |pmid=3144854 |doi= |url=}}</ref> Creating an entire helical structure relies on a set of translational and rotational matrices which are coded in the protein data bank.<ref>{{cite journal |author=Aldrich RA |title=Children in cities--Seattle's KidsPlace program |journal=Acta Paediatr Jpn |volume=29 |issue=1 |pages=84–90 |date=February 1987 |pmid=3144854 |doi= |url=}}</ref> Helical symmetry is given by the formula P=μ x ρ, where μ is the number of structural units per turn of the helix, ρ is the axial rise per unit and P is the pitch of the helix. The structure is said to be open due to the characteristic that any volume can be enclosed by varying the length of the helix.<ref name="virology">{{cite book |author=Racaniello, Vincent R.; Enquist, L. W. |title=Principles of Virology, Vol. 1: Molecular Biology |publisher=ASM Press |location=Washington, D.C |year=2008 |pages= |isbn=1-55581-479-4 |oclc= |doi= |accessdate=}}</ref> The most understood helical virus is the tobacco mosaic virus.<ref>{{cite journal |author=Yamada S, Matsuzawa T, Yamada K, Yoshioka S, Ono S, Hishinuma T |title=Modified inversion recovery method for nuclear magnetic resonance imaging |journal=Sci Rep Res Inst Tohoku Univ Med |volume=33 |issue=1-4 |pages=9–15 |date=December 1986 |pmid=3629216 |doi= |url=}}</ref>The virus is a single molecule of (+) strand RNA. Each coat protein on the interior of the helix bind three nucleotides of the RNA genome. Influenza A viruses differ by comprising multiple ribonucleoproteins, the viral NP protein organizes the RNA into a helical structure. The size is also different the tobacco mosaic virus has a 16.33 protein subunits per helical turn,<ref>{{cite journal |author=Yamada S, Matsuzawa T, Yamada K, Yoshioka S, Ono S, Hishinuma T |title=Modified inversion recovery method for nuclear magnetic resonance imaging |journal=Sci Rep Res Inst Tohoku Univ Med |volume=33 |issue=1-4 |pages=9–15 |date=December 1986 |pmid=3629216 |doi= |url=}}</ref> while the influenza A virus has a 28 amino acid tail loop.{{Citation needed}}


==Triangulation number==
==Triangulation number==

Revision as of 21:14, 25 February 2015

Schematic of a Cytomegalovirus
For the leaf bug, see Miridae.

A capsid is the protein shell of a virus. It consists of several oligomeric structural subunits made of protein called protomers. The observable 3-dimensional morphological subunits, which may or may not correspond to individual proteins, are called capsomeres. The capsid encloses the genetic material of the virus.

Capsids are broadly classified according to their structure. The majority of viruses have capsids with either helical or icosahedral[1][2] structure. Some viruses, such as bacteriophages, have developed more complicated structures due to constraints of elasticity and electrostatics.[3] The icosahedral shape, which has 20 equilateral triangular faces, approximates a sphere, while the helical shape is cylindrical.[4] The capsid faces may consist of one or more proteins. For example, the foot-and-mouth disease virus capsid has faces consisting of three proteins named VP1–3.[5]

Some viruses are enveloped, meaning that the capsid is coated with a lipid membrane known as the viral envelope. The envelope is acquired by the capsid from an intracellular membrane in the virus' host; examples include the inner nuclear membrane, the golgi membrane, and the cell's outer membrane.[6]

Once the virus has infected the cell, it will start replicating itself, using the mechanisms of the infected host cell. During this process, new capsid subunits are synthesized according to the genetic material of the virus, using the protein biosynthesis mechanism of the cell. During the assembly process, a portal subunit is assembled at one vertex of the capsid. Through this portal, viral DNA or RNA is transported into the capsid.[7]

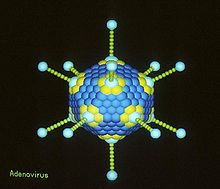
Structural analyses of major capsid protein (MCP) architectures have been used to categorise viruses into families. For example, the bacteriophage PRD1, Paramecium bursaria Chlorella algal virus, and mammalian adenovirus have been placed in the same family.[8]

Specific shapes

Icosahedral

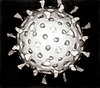
Icosahedral capsid of an Adenovirus

Although the icosahedral structure is extremely common among viruses, size differences and slight variations exist between virions. Given an asymmetric subunit on a triangular face of a regular icosahedron, with three subunits per face 60 such subunits can be placed in an equivalent manner. Most virions, because of their size, have more than 60 subunits. These variations have been classified on the basis of the quasi-equivalence principle proposed by Donald Caspar and Aaron Klug.[9]

An icosahedral structure can be regarded as being constructed from 12 pentamers. The number of pentamers is fixed but the number of hexamers can vary.[10] These shells can be constructed from pentamers and hexamers by minimizing the number T (triangulation number) of nonequivalent locations that subunits occupy, with the T-number adopting the particular integer values 1, 3, 4, 7, 12, 13,...(T = h2 + k2 + hk, with h, k equal to nonnegative integers). These shells always contain 12 pentamers plus 10 (T-1) hexamers. Although this classification can be applied to the majority of known viruses exceptions are known including the retroviruses where point mutations disrupt the symmetry.[10]

Prolate

This is an icosahedron elongated along the fivefold axis and is a common arrangement of the heads of bacteriophages. Such a structure is composed of a cylinder with a cap at either end. The cylinder is composed of 10 triangles. The Q number, which can be any positive integer, specifies the number of triangles, composed of asymmetric subunits, that make up the 10 triangles of the cylinder. The caps are classified by the T number.[11]

Helical

3D model of Helical capsid structure

Many rod-shaped and filamentous plant viruses have capsids with helical symmetry.[12] The helical structure can be described as a set of n 1-D molecular helices related by an n-fold axial symmetry.[13] The helical transformation are classified into two categories: one-dimensional and two-dimensional helical systems.[14] Creating an entire helical structure relies on a set of translational and rotational matrices which are coded in the protein data bank.[15] Helical symmetry is given by the formula P=μ x ρ, where μ is the number of structural units per turn of the helix, ρ is the axial rise per unit and P is the pitch of the helix. The structure is said to be open due to the characteristic that any volume can be enclosed by varying the length of the helix.[16] The most understood helical virus is the tobacco mosaic virus.[17]The virus is a single molecule of (+) strand RNA. Each coat protein on the interior of the helix bind three nucleotides of the RNA genome. Influenza A viruses differ by comprising multiple ribonucleoproteins, the viral NP protein organizes the RNA into a helical structure. The size is also different the tobacco mosaic virus has a 16.33 protein subunits per helical turn,[18] while the influenza A virus has a 28 amino acid tail loop.[citation needed]

Triangulation number

Virus capsid T-numbers

Icosahedral virus capsids are typically assigned a triangulation number (T-number) to describe the relation between the number of pentagons and hexagons i.e. their quasi-symmetry in the capsid shell. The T-number idea was originally developed to explain the quasi-symmetry by Caspar and Klug in 1962.[19]

For example, a purely dodecahedral virus has a T-number of 1 (usually written, T=1) and a truncated icosahedron is assigned T=3. The T-number is calculated by (1) applying a grid to the surface of the virus with coordinates h and k, (2) counting the number of steps between successive pentagons on the virus surface, (3) applying the formula:

=

where and h and k are the distances between the successive pentagons on the virus surface for each axis (see figure on right). The larger the T-number the more hexagons are present relative to the pentagons.[20][21]

For the hexagonal system, the polyhedra have 20T vertices, 30T edges, 10T+2 faces (12 pentagons and 10(T-1) hexagons). For the dual triangular, the vertex and face counts are flipped.

Representation of Viral Capsid T-numbers up to (6,6)
capsid parameters hexagon/pentagon system triangle system
(h,k) T # hex Conway notation image geometric name # tri Conway notation image geometric name
(1,0) 1 0 D Dodecahedron Dodecahedron 20 I Icosahedron Icosahedron
(1,1) 3 20 tI
dkD		 Truncated icosahedron Truncated icosahedron 60 kD Pentakis dodecahedron Pentakis dodecahedron
(2,0) 4 30 cD=t5daD Truncated rhombic triacontahedron Truncated rhombic triacontahedron 80 k5aD 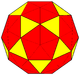Pentakis icosidodecahedron Pentakis icosidodecahedron
(2,1) 7 60 dk5sD Truncated pentagonal hexecontahedron 140 k5sD Pentakis snub dodecahedron
(3,0) 9 80 dktI Hexapentatruncated pentakis dodecahedron 180 ktI Hexapentakis truncated icosahedron
(2,2) 12 110 dkt5daD 240 kt5daD Hexapentakis truncated rhombic triacontahedron
(3,1) 13 120 260
(4,0) 16 150 ccD 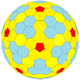320 dccD
(3,2) 19 180 380
(4,1) 21 200 dk5k6stI
tk5sD		 420 k5k6stI
kdk5sD		 Hexapentakis snub truncated icosahedron
(5,0) 25 240 500
(3,3) 27 260 tktI 540 kdktI
(4,2) 28
(5,1) 31
(6,0) 36 350 tkt5daD 720 kdkt5daD
(4,3) 37
(5,2) 39
(6,1) 43
(4,4) 48 470 dadkt5daD 960 k5k6akdk5aD
(6,2) 48
(5,3) 49
(5,4) 61
(6,3) 64
(5,5) 75
(6,4) 76
(6,5) 91
(6,6) 108
...

T-numbers can be represented in different ways, for example T=1 can only be represented as an icosahedron or a dodecahedron and, depending on the type of quasi-symmetry, T= 3 can be presented as a truncated dodecahedron, an icosidodecahedron, or a truncated icosahedron and their respective duals a triakis icosahedron, a rhombic triacontahedron, or a pentakis dodecahedron. [22]

Functions

The functions of the virion are to protect the genome, deliver the genome and interact with the host. The virion must assemble a stable, protective protein shell to protect the genome from lethal chemical and physical agents. These include forms of natural radiation, extremes of pH or temperature and proteolytic and nucleolytic enzymes. Delivery of the genome is also important by specific binding to external receptors of the host cell, transmission of specific signals that induce uncoating of the genome, and induction of fusion with host cell membranes.[16]

Chemical properties

The viral particle must be metastable so that interactions can be reversed readily when entering and uncoating a new host cell. If it attains the minimum free energy state conformation will be irreversible associated with attachment and entry. Each subunit of the capsid has identical bonding contacts with its neighbors, and the two binding contacts are usually noncovalent. The non-covalent bonding holds the structural unit together. The reversible formation of non-covalent bonds between properly folded subunits leads to error-free assembly and minimizes free energy.[16]

See also

References

Wikimedia Commons has media related to Capsid.
  1. ^ Lidmar J, Mirny L, Nelson, DR (2003). "Virus shapes and buckling transitions in spherical shells". Phys. Rev. E. 68 (5): 051910. doi:10.1103/PhysRevE.68.051910.{{cite journal}}: CS1 maint: multiple names: authors list (link)
  2. ^ Vernizzi G, Olvera de la Cruz M (2007). "Faceting ionic shells into icosahedra via electrostatics". Proc. Natl. Acad. Sci. USA. 104 (47): 18382–18386. doi:10.1073/pnas.0703431104.
  3. ^ Vernizzi G, Sknepnek R, Olvera de la Cruz M (2011). "Platonic and Archimedean geometries in multicomponent elastic membranes". Proc. Natl. Acad. Sci. USA. 108 (11): 4292–4296. doi:10.1073/pnas.1012872108. PMC 3060260. PMID 21368184.{{cite journal}}: CS1 maint: multiple names: authors list (link)
  4. ^ Branden, Carl and Tooze, John (1991). Introduction to Protein Structure. New York: Garland. pp. 161–162. ISBN 0-8153-0270-3.{{cite book}}: CS1 maint: multiple names: authors list (link)
  5. ^ "Virus Structure (web-books.com)".
  6. ^ Alberts, Bruce; Bray, Dennis; Lewis, Julian; Raff, Martin; Roberts, Keith; Watson, James D. (1994). Molecular Biology of the Cell (4 ed.). p. 280.{{cite book}}: CS1 maint: multiple names: authors list (link)
  7. ^ Newcomb WW, Homa FL, Brown JC (August 2005). "Involvement of the Portal at an Early Step in Herpes Simplex Virus Capsid Assembly". Journal of Virology. 79 (16): 10540–6. doi:10.1128/JVI.79.16.10540-10546.2005. PMC 1182615. PMID 16051846.{{cite journal}}: CS1 maint: multiple names: authors list (link)
  8. ^ Khayat et al. classified Sulfolobus turreted icosahedral virus (STIV) and Laurinmäki et al. classified bacteriophage Bam35 – Proc. Natl. Acad. Sci. U.S.A. 103, 3669 (2006); 102, 18944 (2005); Structure 13, 1819 (2005)
  9. ^ Caspar DLD, Klug A (1962) Q. Biol. 27, 1–24.
  10. ^ a b Johnson, J. E. and Speir, J.A. (2009). Desk Encyclopedia of General Virology. Boston: Academic Press. pp. 115–123. ISBN 0-12-375146-2.{{cite book}}: CS1 maint: multiple names: authors list (link)
  11. ^ Casens, S. (2009). Desk Encyclopedia of General Virology. Boston: Academic Press. pp. 167–174. ISBN 0-12-375146-2.
  12. ^ Yamada S, Matsuzawa T, Yamada K, Yoshioka S, Ono S, Hishinuma T (December 1986). "Modified inversion recovery method for nuclear magnetic resonance imaging". Sci Rep Res Inst Tohoku Univ Med. 33 (1–4): 9–15. PMID 3629216.{{cite journal}}: CS1 maint: multiple names: authors list (link)
  13. ^ Aldrich RA (February 1987). "Children in cities--Seattle's KidsPlace program". Acta Paediatr Jpn. 29 (1): 84–90. PMID 3144854.
  14. ^ Aldrich RA (February 1987). "Children in cities--Seattle's KidsPlace program". Acta Paediatr Jpn. 29 (1): 84–90. PMID 3144854.
  15. ^ Aldrich RA (February 1987). "Children in cities--Seattle's KidsPlace program". Acta Paediatr Jpn. 29 (1): 84–90. PMID 3144854.
  16. ^ a b c Racaniello, Vincent R.; Enquist, L. W. (2008). Principles of Virology, Vol. 1: Molecular Biology. Washington, D.C: ASM Press. ISBN 1-55581-479-4.{{cite book}}: CS1 maint: multiple names: authors list (link)
  17. ^ Yamada S, Matsuzawa T, Yamada K, Yoshioka S, Ono S, Hishinuma T (December 1986). "Modified inversion recovery method for nuclear magnetic resonance imaging". Sci Rep Res Inst Tohoku Univ Med. 33 (1–4): 9–15. PMID 3629216.{{cite journal}}: CS1 maint: multiple names: authors list (link)
  18. ^ Yamada S, Matsuzawa T, Yamada K, Yoshioka S, Ono S, Hishinuma T (December 1986). "Modified inversion recovery method for nuclear magnetic resonance imaging". Sci Rep Res Inst Tohoku Univ Med. 33 (1–4): 9–15. PMID 3629216.{{cite journal}}: CS1 maint: multiple names: authors list (link)
  19. ^ Caspar, D. L. D. and Klug, A. (1962). "Physical Principles in the Construction of Regular Viruses". Cold Spring Harbor Symp. Quant. Biol. 27: 1–24. PMID 14019094.{{cite journal}}: CS1 maint: multiple names: authors list (link)
  20. ^ Mannige RV, Brooks CL III (2010). "Periodic Table of Virus Capsids: Implications for Natural Selection and Design". PLoS ONE. 5 (3): e9423. doi:10.1371/journal.pone.0009423. PMC 2831995. PMID 20209096.{{cite journal}}: CS1 maint: unflagged free DOI (link)
  21. ^ "T-number index". VIPERdb. La Jolla, CA: The Scripps Research Institute. doi:10.1093/nar/gkn840. Retrieved March 17, 2011. {{cite web}}: External link in |work= (help)
  22. ^ K. V. Damodaran, Vijay S. Reddy, John E. Johnson and Charles L. Brooks III (2002). "A General Method to Quantify Quasi-equivalence in Icosahedral Viruses". J. Mol. Biol. 324 (4): 723–737. doi:10.1016/S0022-2836(02)01138-5. PMID 12460573.{{cite journal}}: CS1 maint: multiple names: authors list (link)
Retrieved from "https://en.wikipedia.org/w/index.php?title=Capsid&oldid=648843382"