Talk:Monty Hall problem
| This is the talk page for discussing changes to the Monty Hall problem article itself. Please place discussions on the underlying mathematical issues on the Arguments page. If you just have a question, try Wikipedia:Reference desk/Mathematics instead. |
| This article is of interest to the following WikiProjects: | |||||||||||||||||||||||||||
| |||||||||||||||||||||||||||
 | Monty Hall problem is a featured article; it (or a previous version of it) has been identified as one of the best articles produced by the Wikipedia community. Even so, if you can update or improve it, please do so. | |||||||||||||||||||||
| This article appeared on Wikipedia's Main Page as Today's featured article on July 23, 2005. | ||||||||||||||||||||||
| ||||||||||||||||||||||
| This is the talk page for discussing improvements to the Monty Hall problem article. This is not a forum for general discussion of the article's subject. |
Article policies
|
| Find sources: Google (books · news · scholar · free images · WP refs) · FENS · JSTOR · TWL |
| Archives: Index, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39Auto-archiving period: 15 days |
 Archives |
|---|
|
Proposed Edit To The Popular solution
I'd like to make this the first solution offered. Attributed to Selvin's 2nd letter; Chun 1991; Grinstead and Snell 2006:137-138),
- Your initial chance of selecting the car is 1/3. This is unchanged by the host revealing a goat. Therefore, when offered, switching doubles your chance of winning the car from 1/3 to 2/3. Glkanter (talk) 13:14, 21 January 2010 (UTC)
- I think the concept is good but the reason why the unchanged chance of having originally chosen the car mean that the chances of winning by switching are 2/3 is afar from obvious to most people. The solution needs further explanation, maybe along the lines of you always get the opposite of your original choice if you swap. Martin Hogbin (talk) 14:31, 21 January 2010 (UTC)
- Actually, my proposal is just a re-write of what's already in there. But, let's flesh out your idea while sticking with reliable sources. There's already 3 sources for the current more-complicated statement in the article. Selvin agrees with Monty Hall that it remains at 1/3 in his 2nd letter to The American Statistician. In his 1st letter, he has a table of all 9 possible outcomes, 3 locations for the car * 3 contestant choices. He lumps each of the the two-goats choice as 1 line item. This chart, which shows all possible outcomes, could accurately be summarized as 'you get the opposite'. (Chun's and Grinstead & Snell's table also shows this 'opposite' result by switching.) Chun and Grinstead & Snell demonstrate the 1/3 in their chart in the Probabilistic section. I guess we could add the chart to the Popular solution. I think it would demonstrate the equivalency of the differing approaches if they both used the same sources. All they do in the chart is divide the original 1/3 contestant door by 2. Then all the contestant does is add the 1/6 & 1/6 back together. And, there are 2 other solutions already provided in the section. Glkanter (talk) 15:11, 21 January 2010 (UTC)
- "This is unchanged by the host revealing a goat." is not what Grinstead and Snell say. I can't find my copy of the Chun reference, but I highly doubt this is what he says either (do you have a copy of this reference, or are you interpreting this from the tree diagram?). What Grinstead and Snell actually say is: "Using the “stay” strategy [deciding beforehand to stay with the initial choice whatever the host does], a contestant will win the car with probability 1/3, since 1/3 of the time the door he picks will have the car behind it. On the other hand, if a contestant plays the “switch” strategy, then he will win whenever the door he originally picked does not have the car behind it, which happens 2/3 of the time." Selvin doesn't say this either - he's quoting Monty Hall. If you want to include the full quote that's fine, but from a sourcing perspective it would be much better to have a secondary source for this.
- And, you're completely missing the point of the table and the tree. The host only opens one door, not both. Before the host opens a door the player's chance is 1/3 (in the tree this is the 1/3 for Door 1 on the left). After the host opens either, but only one, of the doors the player's chance is 1/6 and the other door's chance is 1/3. Viewed as a conditional probability this means the player's chance, in this case, is 1/3 and the other door's chance is 2/3. You don't add the 1/6 and 1/6 to get "the player's chance". You divide 1/6 by the probability of being in this case (which is 1/2). -- Rick Block (talk) 15:45, 21 January 2010 (UTC)
Yes, I am using them as a source based on the diagram showing the Total Probability is 1/6 + 1/6 = 1/3.
Selvin says of Monty Hall's quote, 'I could not have said it better myself'. That means he agrees.
I can use that table any way that is mathematically sound. The column heading is 'Total Probability'. It's really nothing more than Selvin's original table from his first letter reduced to just 1 of 3 random contestant picks, plus the 2-goat options are split out. That I choose to add 1/6 + 1/6 rather than do the unfamiliar division is certainly a valid use of the figures. Just not what the authors expected. Glkanter (talk) 15:56, 21 January 2010 (UTC)
- If you are interpreting the table the words should reflect that. As stated it sounds like you're saying these sources state this in words. To make it clear you're interpreting the table (which is a valid thing to do) I'd suggest you say what it is in the table that you're referring to.
- My point about adding 1/6 plus 1/6 is that by doing this you're determining the player's chance of initially selecting the car (before the host has opened a door). This is the exact point we've been talking about for over year. It is NOT mathematically sound to add these together and call it the chance of the player's door hiding the car after the host has opened a door. This is not what the table shows. It's the chance of initially selecting the car. It is also the chance of winning the car if you ignore what the host does and stick with your original choice. But this 1/3 (=1/6+1/6) is not the chance in effect after the host has opened a door (say Door 3) where the opened door's chance is now 0. If you're saying the player's door's chance is 1/3 because it's 1/6+1/6, the chance of either of the other doors (by the same logic) is 0+1/3. The opened door's chance is 0 only conditionally, i.e. 0 divided by 1/2. Its total probability (considering all cases) is STILL 1/3! Look at the table. The other door's chance is 2/3 only conditionally, i.e. 1/3 divided by 1/2 - but its total probability is also still 1/3. Similarly, the original door's chance after the host has opened a door is also only the conditional chance, i.e. 1/6 divided by 1/2. The numeric answer is 1/3 which is the same number as its total probability considering all cases, but where this number comes from (according to the table) is not 1/6+1/6 "unchanged" by the host opening a door. It's the original 1/3, divided into two pieces (reflecting the cases where the host opens door 2 and door 3), and then divided by the probability of these cases (which is 1/2). The result is the numeric probability doesn't change, but the reason for this, as shown by the table or the tree, is that it splits it into 1/6 and 1/6 and then becomes 1/3 only as a conditional probability (i.e. by dividing by 1/2). -- Rick Block (talk) 18:03, 21 January 2010 (UTC)
- The tables in the Probabilist solution section are derived from Selvin's first letter. He lists 9 cases and determines 3 lose when switching, for 1/3. The Probabilistic section's table shows only 1 of the 3 random contestant choices (door #1) and splits out the 1/3 for 2 goats by dividing by 2 for 1/6 and 1/6. This gives 2 cases at 1/3 each and 2 cases at 1/6 each in the Total Probability column of Chun's and Grinstead and Snell's table.
- 1. It looks like you can't solve the conditional problem without also solving the unconditional problem. That's what the 1/6 + 1/6 gives us. From the Total Probability column of the same table they use to solve the conditional problem. I have now solved the problem unconditionally.
- 2. To get to 1/6, they divided Selvin's 1/3 by 2. To solve this conditionally, you're telling me I need to divide by 1/2. OK. To determine my door's probability of having a car, I will divide by 1/2. Which is the same as multiplying by 2. So, (1/3)/2 = 1/6. 1/6 * 2 = 1/3 probability I have chosen a car. I have now solved the problem conditionally.
- 3. Boris suggested "The coexistence of the conditional and the unconditional can be more peaceful." What could be more peaceful than both solution sections referencing the same table of outcomes? Glkanter (talk) 18:48, 21 January 2010 (UTC)
- I'm not sure I'm understanding what you're saying - I'm not arguing here but would like to echo back what I think you're saying.
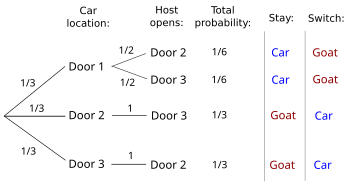
- By the tables in the Probabilistic solution you mean this tree diagram (which is Chun's, not Grinstead and Snell's) and the large table with the images at the end of the section. The diagram and table show only one of the 3 possible initial player picks (i.e. using player picks door 1 as an example). [just a note - these don't derive from Selvin's table. Chun published the tree diagram, and the large table is simply another view of Chun's diagram. Grinstead and Snell's diagram is larger and shows all possibilities, not just the ones involving the player picking door 1]
- 1. The diagram and the table shows the probability across all cases, so you can solve either the conditional or unconditional problem. Unconditionally, if you don't switch you win the car with probability 1/6+1/6 (top two lines of the diagram - middle column in the table) and if you do switch with probability 1/3+1/3 (bottom two lines of the diagram, outer two columns in the table).
- 2. Where the 1/6 comes from is the original 1/3 (the chance of a player who has picked door 1 selecting the car before the host opens a door) divided by 2 (because the host can open either door). To make this the conditional probability you divide by the probability of the case of interest (e.g. host opens door 3) which is 1/2 (from the diagram this is one of the 1/6 lines plus one of the 1/3 lines, from the table it's either the right half or the left half). [just a note - perhaps a little more intuitively, what this is saying is the door you've picked has a 1/6 out of 1/2 chance of hiding the car in the case the host opens door 3] This is the conditional solution.
- 3. Boris suggested peaceful coexistence of the conditional and unconditional - what could be more peaceful than showing both in the same diagram and table?
- You don't explicitly say it, but it sounds like you're suggesting you're OK with using these two figures (Chun's diagram and the table) in both the "Popular" and "Probabilistic" solution sections. Do I have this right? -- Rick Block (talk) 19:33, 21 January 2010 (UTC)
As a component of all the edits I suggested, yes, the 1 table (I already suggested removing the 2nd one) could be added to the Popular solution section. While the 2 1/6 lines are more detailed than necessary, I think we would be OK. Once the reader got to the symmetrical Probabilistic section and saw the same table, he might just grasp the coexistence we're trying to show.
I don't know what you mean by 'outer column'. All the values I referenced come from the 'Total probability' column.
I'm using the conditional method to derive the probability of my door being the car (1/6)/(1/2) which is the same as 1/6 *2. It's a much less complicated formula than door 3's. And it's a more consistent approach to always solve for my door.
I'd like to see some changes in the FAQs, too. Glkanter (talk)
- I'm losing track of all the proposals. And already some time ago I made aa suggestion on this page: Talk:Monty Hall problem/Construction. There you find my proposal for the beginning of the article. Nijdam (talk) 22:16, 22 January 2010 (UTC)
Nijdam, do you intend to unconditionally revert any edits that I make? Do you agree with the reasoning I'm using to propose these changes? Glkanter (talk) 22:50, 21 January 2010 (UTC)
Let's carry on
As I read this discussion between Rick and the guy from the Mediation Committee, we shouldn't do anything different as we wait for the formal mediation.
Accordingly, I will continue proposing, and when appropriate, making changes to the article. Glkanter (talk) 17:07, 22 January 2010 (UTC)
What happens now?
I've shown that Morgan overlooked Selvins' 'the host acts randomly when faced with 2 goats (boxes)'.
Nijdam has been uncommunicative about his intentions and reasons.
I edited the article and Nijdam reverted me. I reverted him back. What's next? Glkanter (talk) 12:33, 23 January 2010 (UTC)
- I've undone it. Your change to the popular solution is not good, because you make an unexplained jump, which is clearly explained in the original. Your changes to the probabilistic solution cannot be done by the argument that you proved Morgan wrong, or similar, which is POV. Morgan did not criticize Selvin anyway. It might me easier for you to make several logical subchanges, with less chance to be undone all. Heptalogos (talk) 13:18, 23 January 2010 (UTC)
- Yes, had Morgan, et al even the vaguest knowledge of the puzzle's history, a simple letter to vos Savant referencing Selvin's 2nd letter would have allowed her, as Selvin also found it necessary, to clarify that the host chose randomly when faced with 2 goats. Glkanter (talk) 14:12, 23 January 2010 (UTC)
- She did not even need to clarify, because it's perfectly reasonable to assume no host bias. But this discussion doesn't make any sense in discussing an encyclopedian article. Heptalogos (talk) 14:19, 23 January 2010 (UTC)
- I think it is best to leave any editing until we get an input from the mediator. So long as this happens within a reasonable time. Martin Hogbin (talk) 13:28, 23 January 2010 (UTC)
- You changed Sources of confusion into 3 parts: 50/50 paradox, assumptions, and (un)conditional. But the last one is hardly explaining the discussions concerning the number of the door. Also, the second one starts with "selvin", out of the sky. Heptalogos (talk) 13:55, 23 January 2010 (UTC)
'Increasing the number of doors' and 'N doors'
'Increasing the number of doors' is in the 'Aids to Understanding' section. 'N doors' is in the variants.
It seems confusing to me that the same idea would be appropriate for both sections. Glkanter (talk) 13:16, 23 January 2010 (UTC)
Sources of confusion
Most of the article's content is about confusion. I see three sources:
1. Incomplete information: we assume worlds outside and/or within the stated problem.
- How is the setup? What is the behavior? What is the knowledge?
2. Surplus information: we decide which information to use and which not.
- Game show, door numbers, host knowledge, talking host.
3. Paradox: the presentation of the information leads to wrong assumptions and decisions.
- A door is not just randomly opened out of three or two, which is the missing key for many.
Source 3 is the basic reason for the problem.
Source 1 is the basic reason for the paradox.
Source 2 is the basic reason for the afterparty disagreements.
The article uses the same order: paradox first, then the assumptions explained, and then the discussion about the details included in or exluded from the conditions. I propose to setup the article using these headers, or similar:
- Problem statement: the usual and the correct answers
- Paradox: simply explained
- Assumptions: reasonableness and explicitness
- Conditions: possibilities and variations
- History: (conflicting) perspectives
- Bayesian analysis
- etc. Heptalogos (talk) 20:13, 23 January 2010 (UTC)
Your section 'Paradox:simply explained' needs to convince people of the right solution. I may not normally be the purpose of an encyclopedia to convince people but, unless readers believe the solution, the rest of the article is wasted. As most people get the answer wrong and many do not believe the answer even when explained to them, this point is of primary importance.
- Split the article into 2 articles: The MHP Problem and Solution, and The MHP's Conflicting Perspectives. Because nobody, other than you guys, gives a shit. Glkanter (talk) 16:58, 24 January 2010 (UTC)
Where will you put the conditional solution? Martin Hogbin (talk) 16:08, 24 January 2010 (UTC)
- I think the article should indeed not be basically explanatory, but that's already done now in the current article, e.g. in the popular solution section. This may be in the Paradox section. We need to end it with the explicit assumptions needed for this simple explanation(s) to be correct, which is then an inroduction to the next chapter. Is it an option to link to this, which is about the best primary source available? This will also provide an opportunity for people to understand it better. Marilyn offers some examples, like the sea shells. If people still don't understand, they should maybe visit an internet forum to discuss.
- The assumptions section will be the introduction to the Conditions section. This seems to be the best section for those sources that go into detail, like Morgan. But Morgan may already be mentioned as a source in the assumptions section, or even in the last part of the Paradox section where the necessary assumptions are given. We'll need a source for that statement anyway. This setup might also be in line with the combined solutions idea of Rick. Heptalogos (talk) 18:48, 24 January 2010 (UTC)
- I'm not seeing a significant difference between what you're suggesting and the current structure. You're missing the WP:LEAD (which needs to summarize the entire article - or is this what you mean by "Problem statement"?), but other than that it seems extremely similar. I think it would be helpful if you mapped out where the existing content (by section) would go in this structure and if you're suggesting deleting anything explicitly mentioning that. Without this, it's a little difficult to understand what you're really talking about. For example, where would the content currently in "Aids to understanding" go? -- Rick Block (talk) 20:32, 24 January 2010 (UTC)
- Roger. I think I need to shuffle this into a new article on my personal page. Nothing needs to be deleted principly. Heptalogos (talk) 20:46, 24 January 2010 (UTC)
For those who don't give a s...
Glkanter: How about near the beginning of the article we state, For a simpler and less comprehensive summary see this version or some such? hydnjo (talk) 20:40, 24 January 2010 (UTC)
- Interesting link from that page. A reliable online source that treats the problem simply. Monty Hall Problem Martin Hogbin (talk) 20:51, 24 January 2010 (UTC)
Is Selvin's Unconditional Solution 'False'
Morgan, without any acknowledgment of Selvin, including his 'equal goat door constraint', calls all unconditional solutions 'false'.
Selvin used a 9 row table (3 car locations * 3 contestant choices) to solve the puzzle he created. Glkanter (talk) 15:02, 25 January 2010 (UTC)
- And, in his initial solution, he didn't make all his assumptions explicit. In his second letter, he said "The basis to my solution is that Monty Hall knows which box contains the keys and when he can open either of two boxes without exposing the keys, he chooses between them at random." [emphasis added] With these qualifications, his initial solution is fine. Without them, not so much. Let's review. Selvin poses the problem and solves it unconditionally. When questioned, he says what the critical assumptions are behind his solution. 16 years later, vos Savant publishes the problem. When questioned, she omits one of the critical assumptions. Morgan et al. (and others) follow through the consequences of omitting this assumption, concluding the probability of winning by switching (without this assumption) is not 2/3 but 1/(1+p) and, if we take p to be 1/2 (which is what the omitted assumption does) the answer is 2/3. If not, we don't exactly know the probability of winning by switching but since it's in the range of 1/2 to 1 it makes sense to switch anyway. The analysis that leads to the 2/3 solution does so regardless of what we assume p is. What Morgan et al. (and others) consider the "proper analysis" doesn't. Does that roughly match your understanding? -- Rick Block (talk) 02:54, 26 January 2010 (UTC)
- You seem to be accepting that in the symmetrical case, a solution that does not distinguish between legal doors opened by the host is acceptable. I agree.
- I also agree that vos Savant failed to make the assumption of symmetry explicit in her explanation, but as I have demonstrated, however you treat the problem the only logical and consistent assumption is that the host chooses a legal door randomly. Martin Hogbin (talk) 09:39, 26 January 2010 (UTC)
Let's review, Rick.
- Selvin introduces his puzzle in The American Statistician
- He solves it unconditionally, with the 9 line table of all possible outcomes
- A few months later he clarifies that Monty Hall knows where the car is, and that Monty Hall chooses randomly when faced with 2 goats
- 15 years later vos Savant answers a reader letter and leaves some of Selvin's premises unstated
- 1 year after vos Savant, while never mentioning Selvin, Morgan claims all unconditional solutions are false. This is also published in The American Statistician, in a piece called 'Let's Make A Deal: The Player's Dilemma', not 'A Critique Of vos Savant's Parade Column'
Selvin's puzzle and solution leave no ambiguities as to the premises, or insistence that it 'must be conditional' or room for 'without certain assumption'. Glkanter (talk) 11:46, 26 January 2010 (UTC)
- I never noticed this. I will add it to my Morgan criticism page. The 'certain assumptions' had already been answered, and in the same journal as the Morgan paper! It makes Morgan's attack on vos Savant even less justified. Unless you assume that Whitaker was asking about one of the many other game shows with one car and two goats ;-) Martin Hogbin (talk) 12:49, 26 January 2010 (UTC)
- Selvin corresponded with Monty Hall himself. Morgan calls their paper, 'Let's Make A Deal: The Player's Dilemma'. There's only 1 game show that these two parties can be talking about. Although Morgan was apparently oblivious to Selvin's letters, and it shows. Glkanter (talk) 14:16, 26 January 2010 (UTC)
- Yes, I was joking. Obviously Morgan are talking about the same show as Selvin. Odd that they did not spot his letters, but that would have spoiled their fun. Martin Hogbin (talk) 17:03, 26 January 2010 (UTC)
- Selvin corresponded with Monty Hall himself. Morgan calls their paper, 'Let's Make A Deal: The Player's Dilemma'. There's only 1 game show that these two parties can be talking about. Although Morgan was apparently oblivious to Selvin's letters, and it shows. Glkanter (talk) 14:16, 26 January 2010 (UTC)
- A few months later he clarifies that Monty Hall knows where the car is, and that Monty Hall chooses randomly when faced with 2 goats
- He solves it as a conditional probability that does not depend in any way on specific door numbers and/or box letters. No mention is made of the possibility that the host might prefer one door/box over another, or that placement might be similarly biased. So it did not address "the conditional problem" as Morgan poses it, and would be lumped in with their "false solutions." JeffJor (talk) 17:39, 26 January 2010 (UTC)
- 15 years later vos Savant answers a reader letter and leaves some of Selvin's premises unstated
- It states the same premises as Selvin's original letter did, and her answer was intentionally worded so as to imply the same premises Selvin clarified. Whether or not you agree she succeeded, she has stated that was her intention.
- 1 year after vos Savant, while never mentioning Selvin, Morgan claims all unconditional solutions are false. This is also published in The American Statistician, in a piece called 'Let's Make A Deal: The Player's Dilemma', not 'A Critique Of vos Savant's Parade Column'
- And conspicuously omitted a dependency that is more important to their solution technique than q, the bias toward opening a specific door. Allowing for placement bias is just as necessary. So they did not address the full "conditional problem," and their solution is just as "false" as those they criticize. We can't use that, I know; but we can acknowledge it in how we use their work.
- Later, the assertion that the MHP is "a conditional problem" that depends on door numbers is reiterated in three other works: Gillman, Grinstead & Snell, and Krauss & Wang. Interstingly, the first two do not justify this assertion, whcih clearly is interpreted by others differently. And the third says it is not true but, that people do use door numbers in the same way that Selvin did, which is not the "conditional problem" Morgan raised.
- The problem continues to appear in popular literature, most publically in the NY Times, and most recently in Leonard Mlodinow's book A Drunkard's Walk: How Randomness Rules Our Lives. None of these treat it as "the conditional problem" as Morgan did; and in fact, their solutions are among what Morgan calls "false." And even when sources acknowledge Morgan's assertion (i.e., Rosenhaus), no discussion of why the problem is important or controversial mentions "the conditional problem" at all. Rosenhaus even says Morgan's issue "was hardly the point at issue between vos Savant and her angry letter-writers," and that "what vos Savant discussed was surely what was intended," thus allowing Morgan's assertion to be discounted, officially, in Wikipedia. JeffJor (talk) 17:39, 26 January 2010 (UTC)
- It is not clear at all that Whitiker's letter - which uses doors, cars, goats, a proffered switch - derived from Selvin - which uses boxes with keys, empty boxes, and an offer to buy the box back for cash (the contestant raises the possibility of a switch). Selvin's game, despite his mispelling "Monte Hall," is true to the game show he mentions, while Whitaker's is not. Vos Savant has even disavowed any connection to it. (It's possible she edited that out.) Morgan treats it the same way, except in their title. Which may be as much a reference to the vernacular usage that led to naming the show "Let's Make A Deal", as to the game show itself. JeffJor (talk) 18:00, 26 January 2010 (UTC)
- That seems a remarkable coincidence to me. Are you seriously suggesting that there is no connection between the two problems?Martin Hogbin (talk) 18:27, 26 January 2010 (UTC)
- It is not clear at all that Whitiker's letter - which uses doors, cars, goats, a proffered switch - derived from Selvin - which uses boxes with keys, empty boxes, and an offer to buy the box back for cash (the contestant raises the possibility of a switch). Selvin's game, despite his mispelling "Monte Hall," is true to the game show he mentions, while Whitaker's is not. Vos Savant has even disavowed any connection to it. (It's possible she edited that out.) Morgan treats it the same way, except in their title. Which may be as much a reference to the vernacular usage that led to naming the show "Let's Make A Deal", as to the game show itself. JeffJor (talk) 18:00, 26 January 2010 (UTC)
- That's what I also raised in "relations between sources". Who thought it to be the same problem? The same question applies to the game theory source mentioned, which is about curtains. I think we only have Vos Savant and all sources explicitly linked to that. All other problems are related, similar, variants, whatever, including three prisoners. Heptalogos (talk) 20:35, 26 January 2010 (UTC)
- Which means that it should be called the "Game Show Problem", which is indeed better. In fact, MHP is not correct at all. Heptalogos (talk) 20:44, 26 January 2010 (UTC)
- Should I put a "citation needed" to "A well-known statement of the problem was published in Parade magazine"? Where's the Monty Hall connection? This seems to have been editor's consensus in the past. In the Dutch article it is even named after a Dutch show host! I don't even care so much about the name, but the quoted phrase above is not in line with "puzzle based on the American television game show". Wiki-rules-Rick, what's your reaction? Heptalogos (talk) 21:54, 28 January 2010 (UTC)
- My statements:
- It's unknown whether the puzzle is based on a specific show.
- There are many puzzles which may be similar to many persons, but for the article we should let the sources decide which are similar and should therefore be mentioned.
- The main source that most sources use is Parade, after which the problem should be named. (Game Show Problem)
- Heptalogos (talk) 22:32, 28 January 2010 (UTC)
- My statements:
- Very interesting this all (See also Keller.), especially for the historic part. What nowadays is called the MHP, is mainly the K&W version, a well defined probability puzzle. And of course one studies weaker versions, like Morgan did. Nijdam (talk) 01:20, 29 January 2010 (UTC)
- That's from a maths perspective, which is quite narrow. Heptalogos (talk) 08:44, 29 January 2010 (UTC)
- There is a long tradition in mathematical and logical puzzles that they should be framed in a way that makes the solution simple and as intended by the originator. Even if there are minor loopholes on the puzzle statement it is usual to overlook these. Martin Hogbin (talk) 10:14, 29 January 2010 (UTC)
The history section of the article mentions Nalebuff's version, which appeared three years before the initial Parade column. Here's his version (reference is in the article):
- The TV game show "Let's Make a Deal" provides Bayesian viewers with a chance to test their ability to form posteriors. Host Monty Hall asks contestants to choose the prize behind one of three curtains. Behind one curtain lies the grand prize; the other two curtains conceal only small gifts. Once the costumed contestant has made a choice, Monty Hall reveals what is behind one of the two curtains that was not chosen. Now, Monty must know what lies behind all three curtains, because never in the history of the show has he ever opened up an unchosen curtain to reveal the grand prize. Having been shown one of the lesser prizes, the contestant is offered a chance to switch curtains. If you were on stage, would you accept that offer and change your original choice?
As far as I know, no one has claimed that this is where Whitaker's version came from or that this version is a restatement of Selvin's, although the similarities in both directions are striking. Dozens of sources refer to the Parade version as the "Monty Hall problem". Since these earlier sources also mention Monty Hall and the problems are obviously isomorphic, saying these are different problems seems like a fairly absurd stance. -- Rick Block (talk) 15:17, 29 January 2010 (UTC)
- What seems absurd to me is that you kept saying that it doesn't matter a bit what we all think is very obvious, because only reliable sources matter. And now you're talking about 'striking similarities' and 'obvious isomorphic problems'. These dozens of sources are very welcome to provide the missing link here, that's all I'm saying. Heptalogos (talk) 21:45, 29 January 2010 (UTC)
- Wait a minute. What I've said all along is that what we all think about whether the problem must be addressed conditionally doesn't matter a bit because only reliable sources matter. What I'm saying here is that reliable sources call "vos Savant's problem" the Monty Hall problem which is the same thing Selvin calls his problem, and that Nalebuff uses the same host (and same problem set up). If this is not enough, I'm perfectly willing to provide more sources. How about Barbeau's literature survey (referenced in the article): "The problem, known variously as Marilyn's Problem, The Monty Hall Problem, and The Car-and-Goats Problem reads as follows ..." BTW, if you're interested in Barbeau's statement of the problem it's this:
- A contestant in a game show is given a choice of three doors. Behind one is a car; ehind each of the other two, a goat. She selects Door A. However, before the door is opened, the host opens Door C and reveals a goat. He then asks the contestant: "Do you want to switch your choice to Door B?" Is it to the advantage of the contestant (who wants the car) to switch?
- And, Barbeau lists as references for this problem Selvin's two letters, vos Savant's Parade columns, Morgan et al., Gillman, Falk, ... (about 40 altogether). -- Rick Block (talk) 02:34, 30 January 2010 (UTC)
- I don't need more sources, I need any source! You did not yet mention one that connects all, but now you mentioned Barbeau. A few others would be welcome indeed, thank you. I am willing to draw the picture, to see how everything is connected. I think this should be part of the article in any way, because otherwise it's not clear what is the scope of the article anyway, and what the scope is based on. Heptalogos (talk) 15:28, 30 January 2010 (UTC)
- Question: Will Rick answer the question directly asked by the section header: Is Selvin's Unconditional Solution 'False'? Glkanter (talk) 03:37, 30 January 2010 (UTC)
- Would Morgan et al. consider this solution a "false" solution? I believe the answer is yes.
- Does Rick believe this solution is "false"? We could talk about this on the/Arguments page if you'd like, however just like I believe for the purposes of this page it does not matter in the least what you think about this, I believe for the purposes of this page it doesn't matter in the least what I think about this. What editors believe (as opposed to what reliable sources say) is completely irrelevant as far as editing is concerned. Will you ever understand this? -- Rick Block (talk) 05:32, 30 January 2010 (UTC)
What editors believe is important, Rick. It says so right here
- "Likewise, exceptional claims in Wikipedia require high-quality reliable sources, and, with clear editorial consensus, unreliable sources for exceptional claims may be rejected due to a lack of quality (see WP:REDFLAG)." Glkanter (talk) 13:31, 30 January 2010 (UTC)
- OK, fine. I'll amend my statement. If something is said by multiple high-quality reliable sources, whether editors agree with it or not is irrelevant. Also see below. -- Rick Block (talk) 02:41, 31 January 2010 (UTC)
FYI
Hate to spoil the conversation but thought y'all might be interested in this. hydnjo (talk) 04:16, 30 January 2010 (UTC)
Yet another source supporting Morgan's POV
See Lucas, Rosenhouse, and Schepler Lucas, Rosenhouse, and Schepler (it's the same Rosenhouse as the recent book). Published in Math. Magazine, 82(5) 332-342 (Dec 2009) - another refereed journal (this is targeted at the undergraduate level, see http://www.maa.org/pubs/mm-guide.html). Some selected quotes:
- "The general principle here is that anything affecting Monty’s decision-making process is relevant to updating our probabilities after Monty opens his door."
- "This [the "high numbered Monty" variant - Monty picks opens the highest numbered door without revealing the car] shows that any proposed solution to the MHP failing to pay close attention to Monty’s selection procedure is incomplete."
They reference vos Savant and Selvin, but not Morgan et al. -- Rick Block (talk) 06:04, 30 January 2010 (UTC)
- I saw nothing in the Lucas and Rosenhouse paper that remotely supports Morgan. In fact, their problem description uses no door #s. I couldn't find those quotes, or references to Selvin or vos Savant. Is that the right link? Glkanter (talk) 10:44, 30 January 2010 (UTC)
- The paper mainly addresses a more general form of the problem including variants where the host is known to pick non-randomly. Obviously in that case 'any proposed solution to the MHP failing to pay close attention to Monty’s selection procedure is incomplete'. The paper has little to do with this article. Martin Hogbin (talk) 12:20, 30 January 2010 (UTC)
- Sorry, it was the wrong link (I've corrected it above). Like Morgan et al., this paper addresses 'Classic Monty" conditionally, even though their problem statement does not use door numbers (!), and addresses variants (including both "High-Numbered Monty" and "Random Monty") to draw attention to the fact that "any proposed solution to the MHP failing to pay close attention to Monty’s selection procedure is incomplete". And, to be clear, the way I read it this quote pertains to ANY version of the MHP - not just variants where the host is known to pick non-randomly. Again, like Morgan et al., they use these variants to show the truth of this statement. -- Rick Block (talk) 14:48, 30 January 2010 (UTC)
- Fine, but you cannot use a variant to prove that a solution relating to the standard problem only is wrong. That would be exactly like using a non-right-angled triangle to prove Pythagoras wrong. Martin Hogbin (talk) 16:52, 30 January 2010 (UTC)
- Sorry, it was the wrong link (I've corrected it above). Like Morgan et al., this paper addresses 'Classic Monty" conditionally, even though their problem statement does not use door numbers (!), and addresses variants (including both "High-Numbered Monty" and "Random Monty") to draw attention to the fact that "any proposed solution to the MHP failing to pay close attention to Monty’s selection procedure is incomplete". And, to be clear, the way I read it this quote pertains to ANY version of the MHP - not just variants where the host is known to pick non-randomly. Again, like Morgan et al., they use these variants to show the truth of this statement. -- Rick Block (talk) 14:48, 30 January 2010 (UTC)
- Yes, but if Pythagoras's logic never used the fact that the triangle is a right triangle, his proof would presumably apply to all triangles not just right triangles. We've been here before and it's really not a very productive argument. Rather than argue about this, I'll pose a question to you (and Glkanter). What is your suggestion for how, in an NPOV manner, to include the POV expressed by multiple reliable sources that unconditional solutions are missing something? In particular, I'm talking about the following (bold added):
- Morgan et al.: Ms. vos Savant went on to defend her original claim with a false proof and also suggested a false simulation ...
- Morgan et al.: Solution F1: If, regardless of the host's action, the player's strategy is to never switch, she will obviously will the car 1/3 of the time. Hence, the probability that she wins if she does switch is 2/3. ... F1's beauty as a false solution is that it is a true statement! It just does not solve the problem at hand.
- Morgan et al.: Solution F2: The sample space is {AGG, GAG, GGA}, each point having probability 1/3, where the triple AGG, for instance, means the auto behind door 1, goat behind door 2, and goat behind door 3. The player choosing door 1 will win in two of these cases if she switches, hence the probability that she wins by switching is 2/3. ... That it [F2] is not a solution to the stated conditional problem is apparent in that the outcome GGA is not in the conditional sample space, since door 3 has been revealed as hiding a goat.
- Gillman: Marilyn's solution goes like this. The chance is 1/3 that the car is actually at #1, and in that case you lose when you switch. The chance is 2/3 that the car is either at #2 (in which case the host perforce opens #3) or at #3 (in which case he perforce opens #2)-and in these cases, the host's revelation of a goat shows you how to switch and win. This is an elegant proof, but it does not address the problem posed, in which the host has shown you a goat at #3.
- Grinstead and Snell: This very simple analysis [as a preselected strategy, staying wins with probability 1/3 while switching wins with probability 2/3], though correct, does not quite solve the problem that Craig posed. Craig asked for the conditional probability that you win if you switch, given that you have chosen door 1 and that Monty has chosen door 3. To solve this problem, we set up the problem before getting this information and then compute the conditional probability given this information.
- Lucas, Rosenhouse, and Schepler: This [the "high numbered Monty" variant - Monty opens the highest numbered door without revealing the car] shows that any proposed solution to the MHP failing to pay close attention to Monty’s selection procedure is incomplete.
- Rosenthal Monty Hall, Monty Fall, Monty Crawl: This solution [what he calls "Shaky Solution" which basically says your original chance of selecting the car is 1/3 and this doesn't change since you knew the host would open a door revealing a goat] is actually correct, but I consider it "shaky" because it fails for slight variants of the problem.
- Let's see. So far we have 2 peer reviewed academic papers (Morgan et al., and Lucas, Rosenhouse and Schepler), a textbook (Grinstead and Snell), an article appearing in American Mathematical Monthly by a past president of the Mathematical Association of America (Gillman), and an article in Math Horizons (another publication of the Mathematical Association of America). All these sources are basically saying the same thing, which is that solutions that don't address the conditional probability of winning by switching are shaky, or incomplete, or don't quite address the problem, or are (most bluntly) false solutions. If these sources aren't sufficient for you, I could find more (but, really, 5 impeccably reliable sources ought to be enough for anyone).
- To repeat, my question is how would you like, in an NPOV manner, to include the POV expressed by these sources that unconditional solutions are missing something? -- Rick Block (talk) 02:31, 31 January 2010 (UTC)
Rick, in the 15 months we have been discussing this, I find that my conclusions upon reading the identical material, Wikipedia policies or MHP sources, are almost never the same as the conclusions you reach. Nothing you cited above causes me to think those sources are capable of telling either Selvin or vos Savant (as proxy for Whitaker) what they 'really' meant, when they both made it so clear in so many ways. In Selvin's MHP, the contestant's original 1/3 can never change, and no outcomes get removed. Only with a different problem, with different premises, can Monty reveal the car, causing the contestant's 1/3 to go to 0, which he cannot do in Selvin's or vos Savant's problem. And the combining doors solution does show an open door #3 with a goat. I could go on extensively, but for what purpose? Glkanter (talk) 05:36, 31 January 2010 (UTC)
- Let's take this one step at a time.
- Do you agree the 5 sources I've cited above are reliable sources by Wikipedia's standards? If not, why not? -- Rick Block (talk) 05:56, 31 January 2010 (UTC)
- Rather than repeat myself here my comprehensive criticism of the Morgan paper can be found here. The paper also has its own criticism published in the same journal in the form of a commentary by Seymann, and many editors here think that it is unreliable. It was, however, published in a peer-reviewed journal so we are obliged to have some reference to it in the article. It is essentially an academic diversion.
- Gillman and G&S just seem to be repeating Morgan with adding anything. They should be included as references to the academic diversion that is described by Morgan.
- Lucas, Rosenhouse, and Schepler show that a different problem requires a different solution. This should be in the variant section.
- Rosenhouse says the simple solution is actually correct, but he considers it shaky because it fails for slight variants of the problem. This is a useful reference as it goes some way to settling some of the debate here. For the symmetrical problem an unconditional solution is correct. Once we add possible variations, such as the host is known to choose a legal door non-randomly, the unconditional solution fails. This might form the basis of a link section between two sections of the article. Martin Hogbin (talk) 12:48, 31 January 2010 (UTC)
- Lucas, Rosenhouse, and Schepler start off by formulating what they consider to be the Monty Hall problem. They are teachers of elmentary university mathematics, and they are anxious to show the power of probability theory. The question they pose is not "would you switch?" but "what would you do to maximize your chances of winning the car?". They make the explicit assumption that when Monty has a choice "he chooses his door randomly". Later it becomes clear that by "randomly" they mean "completely randomly" or "at random, with equal probabilities". They later give the doors equal probabilities 1/3 to be hiding the car, with no reasoning why, except at some point for a side remark "since the doors are identical..." In my opinion these are defects to the paper. They have a tool, probability theory, and they (re)formulate the MHP in order to show off their tool. True, the paper contains a lot of useful references, history, and variants. It takes a long time to discover that they are writing about the conditional version of Monty Hall, even though initially they don't mention any door numbers. It's clear to me why they choose the conditional version: otherwise there wouldn't be much to write! They don't discuss why they have formulated the problem this way; they just make lazy and conventional choices, many of them only implicitly; so they add a whole lot more restrictions to the formulation of the problem as it became famous (in Parade magazine). I don't think the existence of their paper changes the fact that there are several points of view as to "what" the MHP is. Gill110951 (talk) 16:13, 31 January 2010 (UTC)
- Agreed. Many here think the Monty Hall problem is a mathematical puzzle and as such should be formulated in a way that keeps it simple, just like the Three Prisoners Problem is. Martin Hogbin (talk) 16:37, 31 January 2010 (UTC)
- Lucas, Rosenhouse, and Schepler start off by formulating what they consider to be the Monty Hall problem. They are teachers of elmentary university mathematics, and they are anxious to show the power of probability theory. The question they pose is not "would you switch?" but "what would you do to maximize your chances of winning the car?". They make the explicit assumption that when Monty has a choice "he chooses his door randomly". Later it becomes clear that by "randomly" they mean "completely randomly" or "at random, with equal probabilities". They later give the doors equal probabilities 1/3 to be hiding the car, with no reasoning why, except at some point for a side remark "since the doors are identical..." In my opinion these are defects to the paper. They have a tool, probability theory, and they (re)formulate the MHP in order to show off their tool. True, the paper contains a lot of useful references, history, and variants. It takes a long time to discover that they are writing about the conditional version of Monty Hall, even though initially they don't mention any door numbers. It's clear to me why they choose the conditional version: otherwise there wouldn't be much to write! They don't discuss why they have formulated the problem this way; they just make lazy and conventional choices, many of them only implicitly; so they add a whole lot more restrictions to the formulation of the problem as it became famous (in Parade magazine). I don't think the existence of their paper changes the fact that there are several points of view as to "what" the MHP is. Gill110951 (talk) 16:13, 31 January 2010 (UTC)
- I'm now reading Rosenhouse's book. It's nice, in fact much deeper than the Lucas, Rosenhouse, and Schepler (LRS) paper, but still has some strange features. On page 35, at the beginning of Chapter 2: "Classical Monty" he writes down what he calls the canonical version of the problem. As in LRS he doesn't name any doors. His first sentence is "you are shown three identical doors". A lot of pages later, after having discussed many informal solutions and talking a bit about elementary probability, he turns to presenting "the solution". At this point he numbers the doors. We are now 12 pages further on and he wants us to write down probabilities for all the possible initial configurations of (door chosen by, you, door opened by Monty, door hiding the car). For simplicity he focusses on those situations in which you have chosen door 1, so there are only four possibilities (1,2,1),(1,2,3),(1,3,2),(1,3,1). In two of those four, the car is behind door 1. At about this point point he says "it is built into the statement of the problem that the car is equally likely to be behind any of the three doors". Together with the assumption that when the quizmaster has a choice, he chooses with equal probabilities, this forces the four probabilities to be 1/6,1/3,1/3,1/6. Rosenhouse finally computes the probability that switching will give the car, given that you initially chose door 1. Thus he neither solves the unconditional problem, nor the conditional problem (he has not conditioned on the door opened by the quizmaster). Only in the penultimate chapter does he consider explicitly the unconditional problem. BTW he also acknowledges wikipedia for some of his alternative solutions. It seems to me that the authoritative literature shows that there are a lot of different opinions out there, and that it is the charm of the MHP that it allows so many formulations. BTW he has some rude things to say about the Morgan et al paper, in particular, their dogmatic style. Gill110951 (talk) 17:04, 31 January 2010 (UTC)
- @Martin, where does Rosenhouse say the unconditional solution is correct, but shaky? In the situation of total symmetry (all permissable choices by all parties uniform random) it is clear that the conditional and unconditional probabilities must be the same. Prob(switching will give you the car)=Prob(switching will give you the car|Your initial choice)=Prob(switching will give you the car|Your initial choice and door opened by quizmaster; moreover (in the case of total symmetry) Prob(switching gives you car)=1-Prob(not switching gives you car)=1-1/3=2/3. (This symmetry argument was Boris Tsirelson's genial observation). There is absolutely nothing shaky about all this. Without symmetry, conditional probabilities can vary, and we can't know much about them; it is only in pedagogical articles (for students and teachers of elementary probability) by pedantic mathematicians who choose dogmatically to fill in the missing details in such a way that the pretty answer remains true, that we are told dogmatically that everything is "random" or "identical". My POV is that a sensible player chooses her initial door uniformly at random; on being asked whether or not to switch, she'll certainly switch. It doesn't matter which door she happened to choose first, and which door Monty happened to open. Her behaviour is the same. In her situation, it helps not one d*** s*** to answer the question "what is the probability the car is behind the other door, given my initial choice and the door opened by Monty?". The value of this probability depends on a load of things which she doesn't know. And her (or our) "ignorance" does not mean that suddenly various probabilities get fixed at 1/3, 1/2 etc etc. No: her ignorance means that she cannot use her conditional probability (since she has no way of knowing it) as a guide to her choice. Gill110951 (talk) 18:43, 31 January 2010 (UTC)
- Martin meant Rosenthal, not Rosenhouse. A reference above he presumably accidentally deleted that I just restored. -- Rick Block (talk) 19:00, 31 January 2010 (UTC)
- You are quite right Rick. Sorry for the accidental deletion. Martin Hogbin (talk) 20:02, 31 January 2010 (UTC)
Rick, I see none of those sources state that an 'unconditional solution' cannot solve the problem. That is your interpretation. They state that they don't solve the exact problem, e.g. because they don't use the right condition, or don't make the right assumptions. That's what they all say. Heptalogos (talk) 21:36, 31 January 2010 (UTC)
- Right, they state unconditional solutions don't solve the exact problem. Glkanter has brought up the version as of the last FARC (claiming it is full of POV and has been improved since then). Re-reading this I'm actually not seeing the problem. In this version there are two paragraphs between an initial unconditional solution and a conditional solution that say:
- The reasoning above applies to all players at the start of the game without regard to which door the host opens, specifically before the host opens a particular door and gives the player the option to switch doors (Morgan et al. 1991). This means if a large number of players randomly choose whether to stay or switch, then approximately 1/3 of those choosing to stay with the initial selection and 2/3 of those choosing to switch would win the car. This result has been verified experimentally using computer and other simulation techniques (see Simulation below).
- A subtly different question is which strategy is best for an individual player after being shown a particular open door. Answering this question requires determining the conditional probability of winning by switching, given which door the host opens. This probability may differ from the overall probability of winning depending on the exact formulation of the problem (see Sources of confusion, below).
- This structure is very close to how Grinstead and Snell handle this issue (they present an unconditional solution first and then say how this addresses a slightly different question). I assume these are the paragraphs that Glkanter most objects to. Is there any way we can work on these two paragraphs to satisfy everyone's goal of making the article NPOV? -- Rick Block (talk) 22:09, 31 January 2010 (UTC)
- Well, I'm not sure what you mean by 'unconditional solution', but it's good to see your pragmatism by bringing in some article text. I think the first paragraph is POV. The Morgan link probably refers to solution F3, which they call wrong because it does not use the number of the door. However, if the equal goat assumption would have been made, I think Morgan would not have called this wrong. And in the article, this assumption is actually made. That's why it is IMO not correct, but a specific interpretation of Morgan. Heptalogos (talk) 22:34, 31 January 2010 (UTC)
Proposal to complete the popular solution
I only just realized that the "popular solution" just needs the one word "symmetry" added in order to turn it into a mathematically complete and rigorous solution of what we call here the conditional problem, under the further assumptions that many people (but not me) consider the canonical extra conditions. I wrote:
In order to convert this popular story into a mathematically rigorous solution, one has to argue why the probability that the car is behind door 1 does not change on opening door 2 or 3. This can be answered by an appeal to symmetry: under the complete assumptions made above, nothing is changed in the problem if we renumber the doors arbitrarily, and in particular, if we switch numbers 2 and 3. Therefore, the conditional probability that the car is behind door 1, given the player chose 1 and Monty opened 2, is the same as the conditional probability that the car is behind door 1, given the player chose 1 and Monty opened 3. The average of these two (equal) probabilities is 1/3, hence each of them separately is 1/3, too.
Is the missing word "symmetry" the reason that Rosenthal found the unconditional argument "shaky"? If you just say "opening door 3 doesn't change the chance the car is behind door 1" you are certainly being shaky. *Why* doesn't it change the probability? Intuition can so easily be wrong in probability puzzles! So let's make this step in the argument rigorous, rock-solid. Symmetry does that for you.
Mathematicians love using symmetry, since they love to make results obvious, they hate calculations; they are looking for beauty (two important sources of beauty are chance, and symmetry). I notice that non-mathematicians are often not entirely convinced by the symmetry argument. They feel tricked, suspicious. Of course, they are not used to it. Using symmetry is using a meta-mathematical argument, ie, a mathematical argument about mathematical arguments. And such arguing can be tricky, think of Gödel! Gill110951 (talk) 10:31, 1 February 2010 (UTC)
- Looks good to me. I have been arguing here for years that symmetry is a valid reason to accept the unconditional solution, using much the same argument as you. It is also worth noting why Rosenthal found the unconditional solution shaky, this was only because it did not apply to slight variants (such as host chooses non-randomly). Nobody finds Pythatgoras' theorem shaky because it applies only to right angled triangles.
- There is also the argument that random information is no information. That is a standard point of information theory. Again, this argument needs to be carefully made. Martin Hogbin (talk) 13:17, 1 February 2010 (UTC)
- The issue is what source would you use for this? -- Rick Block (talk) 13:34, 1 February 2010 (UTC)
- I won't object the symmetry argument on the ground of lacking source. And to Martin: Gill solves the CONDITIONAL problem! Nijdam (talk) 13:58, 1 February 2010 (UTC)
- I am not the one who is hung up on the conditional/unconditional issue. If you just want to use the word 'conditional' that is fine with me, so long as you do not try to complicate the problem and solution by insisting that it matters which door the host opens, or say that the solution does not address the exact problem 'as asked'. Martin Hogbin (talk) 23:17, 1 February 2010 (UTC)
- I am not the one who is hung up on the use of the word conditional. Never said so. But I do insist that the simple solution, and equivalently the combined doors solution, is not addressing the exact problem 'as asked'. And I want the article to make this clear to the reader. Nijdam (talk) 23:43, 1 February 2010 (UTC)
- Is that not what this thread is all about? If the host chooses randomly then the simple solution does exactly answer the question as asked (after the host has opened a door). The reason - symmetry. Martin Hogbin (talk) 23:49, 1 February 2010 (UTC)
- I am not the one who is hung up on the use of the word conditional. Never said so. But I do insist that the simple solution, and equivalently the combined doors solution, is not addressing the exact problem 'as asked'. And I want the article to make this clear to the reader. Nijdam (talk) 23:43, 1 February 2010 (UTC)
- I am not the one who is hung up on the conditional/unconditional issue. If you just want to use the word 'conditional' that is fine with me, so long as you do not try to complicate the problem and solution by insisting that it matters which door the host opens, or say that the solution does not address the exact problem 'as asked'. Martin Hogbin (talk) 23:17, 1 February 2010 (UTC)
- I won't object the symmetry argument on the ground of lacking source. And to Martin: Gill solves the CONDITIONAL problem! Nijdam (talk) 13:58, 1 February 2010 (UTC)
- No, it doesn't.!Nijdam (talk) 17:33, 2 February 2010 (UTC)
- If i understand that correctly defining symmetry in such a way basically forces the host to pick between 2 goat doors at random with p=1/2 (it seems to be an equivalent assumption). I don't mind to modify the article in such way, but i agree with Rick to the regard that we would need a source for that.--Kmhkmh (talk) 18:00, 1 February 2010 (UTC)
- @Kmhkmh. It's the other way round. Suppose we want to solve the conditional problem. IF the host chooses *uniformly* at random when he has a choice, and IF the car is initially equally likely behind every door, then all the conditional probabilities Prob(car is behind door x| You chose x, Monty Hall opened y), where x,y are any two different door numbers, are the same. In particular,
- Prob(car is behind 1| you chose 1, MH opened 3)
- =Prob(car is behind 1| you chose 1, MH opened 2).
- Prob(car is behind 1| you chose 1, MH opened 3)
- We have been told already that
- Prob(car is behind 1|you chose 1)=1/3.
- But by the law of total probability,
- 1/3 = Prob(car is behind 1|you chose 1) =
- Prob(MH opened 2|you chose 1) x Prob(car is behind 1| you chose 1, MH opened 2)
- + Prob(MH opened 3|you chose 1) x Prob(car is behind 1| you chose 1, MH opened 3)
- 1/3 = Prob(car is behind 1|you chose 1) =
- Denoting the unknown probability by p, we have
- 1/3 = Prob(MH opened 2|you chose 1) x p + Prob(MH opened 3|you chose 1) x p = p
- Gill110951 (talk) 09:35, 2 February 2010 (UTC)
- @Kmhkmh. It's the other way round. Suppose we want to solve the conditional problem. IF the host chooses *uniformly* at random when he has a choice, and IF the car is initially equally likely behind every door, then all the conditional probabilities Prob(car is behind door x| You chose x, Monty Hall opened y), where x,y are any two different door numbers, are the same. In particular,
- If i understand that correctly defining symmetry in such a way basically forces the host to pick between 2 goat doors at random with p=1/2 (it seems to be an equivalent assumption). I don't mind to modify the article in such way, but i agree with Rick to the regard that we would need a source for that.--Kmhkmh (talk) 18:00, 1 February 2010 (UTC)
- Would Selvin's letters satisfy the requirement? Where he says this:
- "The basis to my solution is that Monty Hall knows which box contains the keys and when he can open either of two boxes without exposing the keys, he chooses between them at random." Glkanter (talk) 19:08, 1 February 2010 (UTC)
- Strictly speaking "choosing at random" is not enough, since that does not define the distribution (i.e. you need p=1/2 for each goat door). However "choosing at random" is often meant to implicitly assume a uniform distribution, which is how i would read Selvin's description. Conclusion : If you are picky, there some ambiguity in Selvin's description as well.--Kmhkmh (talk) 20:39, 1 February 2010 (UTC)
- That is getting overly picky. I am sure Selvin meant that the box choice was 'uniform at random'. Martin Hogbin (talk) 23:09, 1 February 2010 (UTC)
- Strictly speaking "choosing at random" is not enough, since that does not define the distribution (i.e. you need p=1/2 for each goat door). However "choosing at random" is often meant to implicitly assume a uniform distribution, which is how i would read Selvin's description. Conclusion : If you are picky, there some ambiguity in Selvin's description as well.--Kmhkmh (talk) 20:39, 1 February 2010 (UTC)
- "The basis to my solution is that Monty Hall knows which box contains the keys and when he can open either of two boxes without exposing the keys, he chooses between them at random." Glkanter (talk) 19:08, 1 February 2010 (UTC)
- Would Selvin's letters satisfy the requirement? Where he says this:
How about the following. I'm not exactly happy with the wording and somebody will have to find appropriate references, but I think this more or less captures what folks are saying.
- <unconditional solution here>
- The reasoning above directly addresses the average probability across all possible combinations of initial player choice and door the host opens (some reference). This means if a large number of players randomly choose whether to stay or switch, then approximately 1/3 of those choosing to stay with the initial selection and 2/3 of those choosing to switch would win the car. This result has been verified experimentally using computer and other simulation techniques (see Simulation below).
- A subtly different question is which strategy is best in a specific case such as that of a player who has picked Door 1 and has then seen the host open Door 3. This difference can also be expressed as whether the player must decide to switch before the host opens a door or is allowed to decide after seeing which door the host opens (Gillman 1992). Because of the symmetry of the problem, the average probability as determined above applies to any specific case as well (this must have a reference). The probability of winning by switching in a specific case can also be determined as a conditional probability, given which doors the player picks and the host opens. Although this is the same as the average probability of winning by switching for the unambiguous problem statement as presented above, in some variations of the problem the conditional probability and average probability may be different, see Variants below.
- <symmetric conditional solution here>
The idea would be to have ONE solution section, sort of like the version as of the last FARC [1] but with these two paragraphs between the unconditional and conditional solutions. -- Rick Block (talk) 04:32, 2 February 2010 (UTC)
- The simple symmetrical solution does address the question 'which strategy is best in a specific case such as that of a player who has picked Door 1 and has then seen the host open Door 3?'. If the host action is random, it does not matter that the host has opened a specific door, because we know that the door opened makes no difference, by reason of symmetry. Can any one else explain this better? Martin Hogbin (talk) 09:15, 2 February 2010 (UTC)
- I have tried Martin, above Gill110951 (talk) 09:35, 2 February 2010 (UTC)
- To be specific: "The (simple) symmetrical solution" is just a way of calculating the CONDITIONAL probability, without using Bayes' formula. I put simple between brackets, because it is not simpler than the solution using Bayes'.Nijdam (talk) 17:33, 2 February 2010 (UTC)
- On the other hand if, between the two solutions we had something like, If it is considered that the host might not choose between the two available doors randomly, the door actually opened by the host may give information which changes the probability that the player has originally chosen the car and thus it becomes important whether the player must decide to switch before the host opens a door or is allowed to decide after seeing which door the host opens (Gillman 1992) I would be happy. Martin Hogbin (talk) 09:37, 2 February 2010 (UTC)
Sources present three different kinds of solutions
Does anyone disagree that most solutions presented in sources are one of the following three types:
1) Completely unconditional, i.e chance of initially picking the car is 1/3 and a goat 2/3, and if you switch these flip.
2) Assuming the player has picked (for example) door 1, i.e. vos Savant's table:
| Door 1 | Door 2 | Door 3 | result if switching |
|---|---|---|---|
| Car | Goat | Goat | Goat |
| Goat | Car | Goat | Car |
| Goat | Goat | Car | Car |
3) Assuming the player has picked (for example) door 1, conditional given the host has opened (for example) door 3, e.g. any of the "conditionalists". These end up as (1/3) / (1/3 + 1/6) = 2/3.
There is clearly conflict among sources about these solutions and clearly conflict among editors about these solutions, so how about a single solution section somewhat like this:
- Solution
- Different sources present solutions to the problem
that directly address slightly different mathematical questionsusing a variety of approaches.
The average probability of winning by switchingSimplest approach
This is the simplest kind of solution.The player initially has a 1/3 chance of picking the car. The host always opens a door revealing a goat, so if the playerignores what the host does anddoesn't switch the player has a 1/3 chance of winning the car. Similarly, the player has a 2/3 chance of initially picking a goat and if the player switches after the host has revealed the other goat the player has a 2/3 chance of winning the car. (some appropriate reference, perhaps Grinstead and Snell)
- What this solution is saying is that if 900 contestants all switch, regardless of which door they initially pick and which door the host opens about 600 would win the car.
The probability of winning by switching givenEnumeration of all cases where the player picks Door 1
- If the player has picked, say, Door 1, there are three equally likely cases.
| Door 1 | Door 2 | Door 3 | result if switching |
|---|---|---|---|
| Car | Goat | Goat | Goat |
| Goat | Car | Goat | Car |
| Goat | Goat | Car | Car |
- A player who switches ends up with a goat in only one of these cases but ends up with the car in two, so the probability of winning the car by switching is 2/3. (some appropriate reference, perhaps vos Savant)
- What this solution is saying is that if 900 contestants are on the show and roughly 1/3 pick Door 1 and they all switch, of these 300 players about 200 would win the car.
- The probability of winning by switching given the player picks Door 1 and the host opens Door 3

- This is a more complicated type of solution involving conditional probability. The difference between this approach and the previous one can be expressed as whether the player must decide to switch before the host opens a door or is allowed to decide after seeing which door the host opens (Gillman 1992).
- The probabilities in all cases where the player has initially picked Door 1 can be determined by referring to the figure below or to an equivalent decision tree as shown to the right (Chun 1991; Grinstead and Snell 2006:137-138 presents an expanded tree showing all initial player picks). Given the player has picked Door 1, the player has a 1/3 chance of having selected the car. Referring to either the figure or the tree, if the host then opens Door 3, switching wins with probability 1/3 if the car is behind Door 2 but loses only with probability 1/6 if the car is behind Door 1. The sum of these probabilities is 1/2, meaning the host opens Door 3 only 1/2 of the time. The conditional probability of winning by switching for players who pick Door 1 and see the host open Door 3 is computed by dividing the total probability (1/3) by the probability of the case of interest (host opens Door 3), therefore this probability is (1/3)/(1/2)=2/3.
- Although this is the same answer as the simpler solutions for the unambiguous problem statement as presented above, in some variations of the problem the conditional probability may differ from the average probability and the probability given only that the player initially picks Door 1, see Variants below. Some proponents of solutions using conditional probability consider the simpler solutions to be incomplete, since the simpler solutions do not explicitly use the constraint in the problem statement that the host must choose which door to open randomly if both hide goats (multiple references, e.g. Morgan et al., Gillman, ...).
- What this type of solution is saying is that if 900 contestants are on the show and roughly 1/3 pick Door 1, of these 300 players about 150 will see the host open Door 3. If they all switch, about 100 would win the car.
- A formal proof that the conditional probability of winning by switching is 2/3 is presented below, see Bayesian analysis.
I'm not overly attached to any of the specific wording used, but I think presenting these as three different types of solutions and including with the last one the essence of the controversy is an NPOV approach. -- Rick Block (talk) 15:41, 2 February 2010 (UTC)
Responses
It is just the same old thing again. Nobody is interested in the average probability of winning by switching. The only question to be answered is the probability after the player has chosen a door (say door 1) and the host has opened another door to reveal a goat (say door 3). If the host chooses randomly which legal door to open then this probability is always exactly 2/3 and, by reason of symmetry, the simple table at the top of this section is a mathematically valid solution. The, so called, condition, that the host has opened a specific door is irrelevant because it can be shown that the probability of interest is independent of the door opened in the symmetrical case.
- That's not quite true for 2 reasons in particular:
- 1.) the average probability provides a reasonable heuristic (in particular if no exact knowledge regarding the influence of the conditions is given). Generally due to the lack of better information people assume the total probability (average) to hold for subsets as well (=being approximately identically with the true conditional probability) unless you have specific data for a subset telling you so or you have some very good reason to believe that this subset differs from the total set regarding a property influencing the probability.
- 2.) Many (probably even most or all) unconditional approaches in reputable literature do make an argument based on the average (total) probability (this includes in particular vos Savant, Devlin, Henze, Behrens). and we need to summarize what the sources do and not how we might improve or extend on them as the latter would be WP:OR.
- --Kmhkmh (talk) 14:09, 4 February 2010 (UTC)
- That's not quite true for 2 reasons in particular:
- If he host chooses a legal door randomly, the probability of winning by switching given the host has opened door 3 is 2/3, given the host has opened door 2 it is 2/3, and the average is also 2/3. There is no condition. Martin Hogbin (talk) 22:41, 5 February 2010 (UTC)
- I don't quite see what this has to do with the 2 points above.--Kmhkmh (talk) 01:18, 6 February 2010 (UTC)
- If he host chooses a legal door randomly, the probability of winning by switching given the host has opened door 3 is 2/3, given the host has opened door 2 it is 2/3, and the average is also 2/3. There is no condition. Martin Hogbin (talk) 22:41, 5 February 2010 (UTC)
- Somehow it looks as if you, like others, desperately are seeking a way of reasoning, to avoid conditioning. But there is none! Try to formulate your above reasoning in formulas, and you will see. BTW. what do you mean with: "the probability of interest is independent of the door opened in the symmetrical case". Nijdam (talk) 23:25, 2 February 2010 (UTC)
- Is this not the same discussion that we are having elsewhere? If the host chooses a legal door uniformly at random then you agree that the probability of interest (probability of winning by switching) is exactly 2/3 whichever door the host opens. In other words the probability of interest is independent of the door number opened by the host. I can show this more formally if you like.
- Since the probability of interest is independent of the door number opened by the host, the door number opened by the host need not be a condition of the problem, by your own argument. Martin Hogbin (talk) 23:35, 2 February 2010 (UTC)
Regarding what sources say, the sources that give the simple solutions do not in any way say that their solutions apply to a different problem or that they are only average solutions. The sources that present simple solutions present them as complete solutions to the question as asked. Martin Hogbin (talk) 16:09, 2 February 2010 (UTC)
- Are you denying that the simplest (fully unconditional) solutions literally address the average probability of winning by switching, or that (say) vos Savant's solution literally addresses the probability of winning by switching given the player picks Door 1? The solution vos Savant presents (for example) includes cases where the host opens Door 2, so it is clearly not directly addressing the conditional probability where the player has chosen a door (say door 1) and the host has opened another door to reveal a goat (say door 3). As far as I know, that the sources offering these solutions present them as "complete" solutions is only implied by these sources. I'm attempting to do the same thing here - they're in the "Solution" section, hence these are by implication complete solutions.
- I think it's fairly clear these are the three typical sorts of solutions that are presented. If you find the words I've used to describe them POV, can you suggest a way to describe them that you don't find POV? -- Rick Block (talk) 21:24, 2 February 2010 (UTC)
- I do agree that the simplest solutions address the average probability of winning by switching, it is just that nobody cares about this. Vos Savant, in common with many editors here, obviously believes that, in the symmetrical case, the door numbers are of no relevance to the problem. Thus a solution presented in which the host opens door 2 is equally valid if the host opens door 3, which of course it is, by symmetry. This especially true as it is not clear that Whitaker even intends to specify door numbers.
- I am not sure what you mean by your second point. Several reliable sources present simple solutions without any form of reservation or restriction. Thus they clearly are asserting that they are answering the question as asked. Some other sources say, to varying degrees, that they are wrong. Martin Hogbin (talk) 23:26, 2 February 2010 (UTC)
- The second point? About vos Savant's solution including cases where the host opens Door 2? The question asks about the case where the player has picked, say, Door 1 and the host has opened, say, Door 3. The table shows the (unconditional) probabilities where the player picks Door 1 and the host opens Door 2 and (not or) the host opens Door 3. What this table literally shows are the unconditional probabilities where the player has initially selected Door 1 - i.e. the player is not looking at either door the host has opened but is thinking about all cases. To analyze the situation after the host has opened a door without caring about the door numbers, call them A, B, and C. The player has selected Door A and the host has opened Door C while Door B remains closed. With this set up, the probability of winning where the host has opened Door B is "this case didn't happen", not 1/3. There's only one case, the player picked Door A and the host opened Door C. This is a conditional case. This is the point Nijdam keeps making that you keep ignoring. The probability of the car being behind A,B, or C is initially 1/3 for each. After the host opens Door C its probability is now 0 (no longer 1/3). What are the other door's probabilities? The question is asking what are their conditional probabilities. -- Rick Block (talk) 01:13, 3 February 2010 (UTC)
- This is about where we started some years ago. In the symmetrical case, the fact that a specific door has been opened reduces the options available to the player but does not affect the probability of interest. It is therefore not a condition. I suggest that we continue this discussion in the section that I have set up on the arguments page. Martin Hogbin (talk) 09:46, 3 February 2010 (UTC)
- Indeed, and you still don't get it. You're still talking about the value 2/3, where we have explained over and over it is not the value that counts, but the nature of the probability. We demonstrated that opening of a door is a condition, and still you persist in saying it is not. What is your intention? Nijdam (talk) 12:53, 3 February 2010 (UTC)
- 'demonstrated that opening of a door is a condition' is exactly what you have not done. You have asserted this several times and also suggested reasons why the event should be considered a condition. I have shown all these reasons to be invalid. I suggest we continue on the appropriate section on the arguments page. Martin Hogbin (talk) 13:58, 3 February 2010 (UTC)
- Indeed, and you still don't get it. You're still talking about the value 2/3, where we have explained over and over it is not the value that counts, but the nature of the probability. We demonstrated that opening of a door is a condition, and still you persist in saying it is not. What is your intention? Nijdam (talk) 12:53, 3 February 2010 (UTC)
- This perhaps should go elsewhere, but Martin if I've picked Door 1 and the host has opened Door 3 what lines of the table do I look at to figure out my probability of winning by switching? The table looks wrong to me since it says the probability of the car being behind Door 3 is 1/3. It clearly isn't anymore. The probabilities inferred from this table are prior probabilities - those that are in effect before the host opens a door. To convey what you're saying it conveys, this table should really only have two lines, a Door 1 line and a "Door 2 or Door 3" line. This makes the probabilities inarguably unconditional, which I think is what you're saying - but then it's clearly showing the probability of winning given the player has picked Door 1 (which you seem to object characterizing it as). -- Rick Block (talk) 18:23, 3 February 2010 (UTC)
- Thus we should, in the article, present the simple solutions in the same way that they are presented by the sources that give them, as complete solutions without reservation or restriction to the exact question that was asked. Martin Hogbin (talk) 23:37, 2 February 2010 (UTC)
- How about the changes as above? Better? -- Rick Block (talk) 01:13, 3 February 2010 (UTC)
- Better, but you still have, 'so if the player ignores what the host does', and 'What this solution is saying is that if 900 contestants all switch, regardless of which door they initially pick and which door the host opens about 600 would win the car'. Later on, in the conditional solution section, you say, 'This is a more complicated type of solution involving conditional probability. The difference between this approach and the previous one can be expressed as whether the player must decide to switch before the host opens a door or is allowed to decide after seeing which door the host opens (Gillman 1992)'.
- My first two quotes should go completely, they are your POV concerning sources that give simple solutions, there are several sources giving a simple solution that do not say what you say.
- Regarding, 'This is a more complicated type of solution involving conditional probability....'. We are now talking about the link between the sections and sources. This should therefore start with something like, 'Some sources treat the problem as requiring the use of conditional probability...' preferably including 'this is important if the host may not choose randomly which door to open, when he has a choice...' Martin Hogbin (talk) 09:46, 3 February 2010 (UTC)
- I've struck "player ignores what the host does". I'm reluctant to strike the 600 out of 900 win bit. You agreed above this solution is literally addressing the average probability. Is it the numbers you object to or the "regardless of which door ..." wording?
- I am not sure what you mean by average probability here. What you say is quite correct, but why mention it?. In the symmetrical case the probability of winning by switching is 2/3 if the host opens door 3, 2/3 if the host opens door 2, and 2/3 on average. Martin Hogbin (talk) 22:44, 3 February 2010 (UTC)
- And the chance is also 2/3 that a random picked child of one of my neighbours is a boy. Nijdam (talk) 23:53, 5 February 2010 (UTC)
- The "difference between this approach" needs to go somewhere. The point is not to say conditional probability is required, but to explain what it means. The tone I'm trying to hit is "an alternate approach", not "the correct approach". Your suggested addition about the importance is your POV, which as far as I recollect no one's ever offered up a source for (just WP:OR) - and addressing the problem using conditional probability is certainly a valid approach whether the host chooses randomly or not. -- Rick Block (talk) 18:23, 3 February 2010 (UTC)
- Your last point is the one to focus on. The simple solution only applies if the host is taken to choose a legal door randomly, it fails if the host chooses non-randomly. Martin Hogbin (talk) 22:44, 3 February 2010 (UTC)
- To make that argument you actually need a conditional approach.--Kmhkmh (talk) 14:13, 4 February 2010 (UTC)
- Your last point is the one to focus on. The simple solution only applies if the host is taken to choose a legal door randomly, it fails if the host chooses non-randomly. Martin Hogbin (talk) 22:44, 3 February 2010 (UTC)
- Yes I agree, but you do not need the conditional approach just to show that the simple argument is valid in the symmetrical case. See my discussion with Nijdam on the arguments page. Martin Hogbin (talk) 15:06, 4 February 2010 (UTC)
- No, no, no. The simple argument is never valid, i.e. for the MHP where the offer to switch is given AFTER the goat door is opened. The probability of interest is the conditional probability. It may be calculated in a lot of ways, with Bayes', with symmetry, etc., but it IS a conditional probability! Nijdam (talk) 23:49, 5 February 2010 (UTC)
- This remains just an assertion on your part. We are currently discussing this subject on the arguments page. Martin Hogbin (talk) 00:44, 6 February 2010 (UTC)
Nice discussion. My present point-of-view is written up (for mathematicians) in http://arxiv.org/abs/1002.0651 (eprint/prepublication archive). I have also submitted it to a peer-reviewed journal. But I already see that I want to improve the symmetry solution, and to add equivalent verbal proofs next to each mathematical proof, so that ordinary people can read it too. Suggestions for improvement are welcome. Gill110951 (talk) 08:09, 4 February 2010 (UTC)
Rick wrote: "this table should really only have two lines, a Door 1 line and a "Door 2 or Door 3" line. This makes the probabilities inarguably unconditional". Rick, given that "door2 or door3" is opened, it's a conditional probability just the same? Heptalogos (talk) 21:54, 5 February 2010 (UTC)
- Well, sort of, but with only two lines (the 2nd line is "car behind Door 2 or Door 3") the condition "door 2 or door 3 opened" (more) obviously does not reduce the sample space. A table with number of samples might help clarify what I'm saying:
| Door 1 | Door 2 | Door 3 | result if switching | total cases | cases if host opens Door 2 or Door 3 |
|---|---|---|---|---|---|
| Car | Goat | Goat | Goat | 100 | ? |
| Goat | Car | Goat | Car | 100 | ? |
| Goat | Goat | Car | Car | 100 | ? |
- What "in two out of three equally likely cases switching wins" means is in 200 out of 300 cases switching wins - it's not saying anything at all about the column with the question marks. The cases are only obviously equally likely before the host opens a door. Looking at this table can you fill in the ? entries based on knowing the host opens "Door 2 or Door 3"?
- I'll give you a hint: focus on the row where the car is behind Door 1. In how many of these 100 cases does the host open Door 2 or Door 3?
- The point is if all you know is the host opens "Door 2 or Door 3", the numbers are ALL still 100 (!). The host opens Door 2 or Door 3 in ALL 300 cases. Asking what happens after the host opens "Door 2 or Door 3" is the same thing as asking what the situation is before the host opens a door. It's the same set of cases, i.e. the same sample set. All the before and after probabilities are the same.
- If we do the same thing with the 2 line table, here's what happens
| Where's the car | result if switching | total cases | cases if host opens Door 2 or Door 3 |
|---|---|---|---|
| Behind Door 1 | Goat | 100 | ? |
| Behind Door 2 or Door 3 | Car | 200 | ? |
- The ? entries in this table are (more) clearly 100/200 (right?). Wherever the car is, the host always opens Door 2 or Door 3. The confusion about whether the ? in the row where the car is behind door 1 should be 100 or 50 pretty much goes away. This confusion is exactly what Morgan et al. are referring to when they say "The distinction between the conditional and unconditional situations here seems to confound many".
- In my opinion (some WP:OR), a better table would be like this:
| Door 1 | Door 2 | Door 3 | total cases | host opens Door 2 | host opens Door 3 | ||
|---|---|---|---|---|---|---|---|
| cases | result if switching | cases | result if switching | ||||
| Car | Goat | Goat | 100 | 50 | Goat | 50 | Goat |
| Goat | Car | Goat | 100 | 0 | N/A | 100 | Car |
| Goat | Goat | Car | 100 | 100 | Car | 0 | N/A |
- And the explanation becomes, "in two equally likely cases (host opens Door 2 or host opens Door 3), switching wins twice as often as staying". The key to the solution is not that the car is equally likely to be behind each door before the host opens a door (this is obvious to everyone), but that it's equally likely that the host open either door and in each case you're twice as likely to win by switching. -- Rick Block (talk) 04:26, 6 February 2010 (UTC)
- The sample space is anyway reduced by opening a door:
| Door picked | Door unopened | Door opened | result if switching | total cases | cases if door is opened |
|---|---|---|---|---|---|
| Car | Goat | Goat | Goat | 100 | 50 |
| Goat | Car | Goat | Car | 100 | 100 |
| Goat | Goat | Car | Car | 100 | 0 |
- You're so close! However there's a problem in your table. In the "Door opened" (3rd) column, the last row says it has a car. This cannot happen. So, in this row, the number in the "total cases" column must be 0. The basic problem is if you want to show a 100/100/100 column (before the host opens a door) and a 50/100/0 column (after the host opens a door) you have to individually identify the doors. You could call them doors A,B,C if you'd like, but you might as well just stick with 1,2,3. The 50/100/0 column can only exist if you know which door the host has opened. It is a conditional case. I suspect what you're really going for is something sort of like this
| Door picked | Unpicked door A | Unpicked door B | result if switching | total cases | cases if host opens Door B |
|---|---|---|---|---|---|
| Car | Goat | Goat | Goat | 100 | 50 |
| Goat | Car | Goat | Car | 100 | 100 |
| Goat | Goat | Car | Car | 100 | 0 |
- The point is the so-called condition "host opens door 2 or door 3" does not have an "exclusive or" sort of sense (meaning a specific one of these doors) but only a "union" sort of sense (meaning all cases where the host opens either door 2 or door 3, i.e. all cases). This is why the ? entries in the first table above are all 100. If you want a conditional case (a 50/100/0 column), the condition has to be "host opens a specific door". Given the problem statement, you might as well stick with Door 3 - it's representative of any other specific case.
- If you're really aiming for the Door A/Door B table, what is your description for why the probability of winning by switching is 2/3 and why the top number in the "cases if host opens Door B" (last) column is 50 and not 100? I assume your explanation doesn't start with "in 2 out of 3 equally likely cases ..." And, BTW, if this had been vos Savant's table I'd imagine the Morgan et al. paper would have never been written. -- Rick Block (talk) 17:46, 6 February 2010 (UTC)
- It's hopeful to see that you don't like 'impossibilities' in the sample space. For now, let's keep focused on the given method. In your example door3 has a car, which is of course just as impossible. You are confusing the situation before with the situation after. Heptalogos (talk) 18:20, 6 February 2010 (UTC)
- In which example? My WP:OR table above? I thought it was obvious the first several columns are the before state, and the last were the after state. My point all along has been the 100/100/100 (or 1/3:1/3:1/3) distribution is obviously the case only in the before state. We could explicitly label the columns if that helps. This makes the table equivalent to the large figure at the end of the Probabilistic solution section of the article.
| Situation BEFORE the host opens a door | Situation AFTER the host opens a door | ||||||
|---|---|---|---|---|---|---|---|
| Door 1 | Door 2 | Door 3 | total cases | host opens Door 2 | host opens Door 3 | ||
| cases | result if switching | cases | result if switching | ||||
| Car | Goat | Goat | 100 | 50 | Goat | 50 | Goat |
| Goat | Car | Goat | 100 | 0 | N/A | 100 | Car |
| Goat | Goat | Car | 100 | 100 | Car | 0 | N/A |
- Anything talking about "2 out of 3 equally likely cases" must be talking about the before state. Are you disagreeing with this? -- Rick Block (talk) 18:40, 6 February 2010 (UTC)
- Yes. But what I mean is that my "door opened" which has a car is the same as your door3 with a car. This is only impossible after we know it has been opened. Before that, I don't identify doors 2 and 3 individually. One can look at the number 3 and always open it, or one can open a door and always number it as 3; there's no relevance in the difference. Unless you assume that a "number bias" may exist. Heptalogos (talk) 19:07, 6 February 2010 (UTC)
- But then, to be consistent, the before condition must be 100/200, not 100/100/100. The door you're opening is one of the 200 that is not door 1, not one of either of the 100 that is door 2 or door 3. You're talking about the 2-line table. -- Rick Block (talk) 19:52, 6 February 2010 (UTC)
- It is known that the 200 cases are equally divided over the two doors without the need to identify them individually. It's conditional because opening one of the doors reduces the sample space. Heptalogos (talk) 20:17, 6 February 2010 (UTC)
I love it
Can I just say Monte Halperin turns 89 this summer and I think he would never have imagined the role he has assumed in this fascinating mathematical back-and-forth. I've watched this page for some time, and very much enjoy the discussions. My humble suggestion to involved editors is to remember what brought you here in the first place, which I'm guessing are the deliciously captivating counter-intuitive qualities of the Monty Hall problem. I hope you can edit collaboratively to communicate and elucidate this to readers! Respectfully, RomaC (talk) 17:54, 6 February 2010 (UTC)
- Was Monty the first in the world to reveal small prices and offer to switch? Or did he copy the act? I heard the puzzle on television and indeed had my 50/50 answer ready. But that was because of the problem statement which didn't make clear that the host would always do that. So I checked it out on Wikipedia and understood the paradox, but there I met some people who were convinced that the number of the door had any significant information or relevance. I am still trying to show them that it hasn't, and for sure wasn't meant to have any relevance. Heptalogos (talk) 18:31, 6 February 2010 (UTC)
- FA-Class Statistics articles
- Mid-importance Statistics articles
- WikiProject Statistics articles
- FA-Class mathematics articles
- Mid-priority mathematics articles
- Wikipedia featured articles
- Featured articles that have appeared on the main page
- Featured articles that have appeared on the main page once
- Old requests for peer review