Chi-squared distribution

This article is about the mathematics of the chi-square distribution. For its uses in statistics, see chi-square test. For the music group, see Chi2 (band).

Probability density function
Cumulative distribution function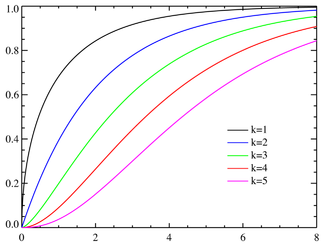
Notation	$\chi ^{2}(k)\!$ or $\chi _{k}^{2}\!$
Parameters	k ∈ N1 — degrees of freedom
Support	x ∈ [0, +∞)
PDF	${\frac {1}{2^{k/2}\Gamma (k/2)}}\;x^{k/2-1}e^{-x/2}\,$
CDF	${\frac {1}{\Gamma (k/2)}}\;\gamma (k/2,\,x/2)$
Mean	k
Median	$\approx k{\bigg (}1-{\frac {2}{9k}}{\bigg )}^{3}$
Mode	max{ k − 2, 0 }
Variance	2k
Skewness	$\scriptstyle {\sqrt {8/k}}\,$
Excess kurtosis	12 / k
Entropy	${\frac {k}{2}}\!+\!\ln(2\Gamma (k/2))\!+\!(1\!-\!k/2)\psi (k/2)$
MGF	(1 − 2 t)−k/2   for  t  < ½
CF	(1 − 2 i t)−k/2

In probability theory and statistics, the chi-square distribution (also chi-squared or χ²-distribution) with k degrees of freedom is the distribution of a sum of the squares of k independent standard normal random variables. It is one of the most widely used probability distributions in inferential statistics, e.g. in hypothesis testing or in construction of confidence intervals. When there is a need to contrast it with the noncentral chi-square distribution, this distribution is sometimes called the central chi-square distribution.

The chi-square distribution is used in the common chi-square tests for goodness of fit of an observed distribution to a theoretical one, the independence of two criteria of classification of qualitative data, and in confidence interval estimation for a population standard deviation of a normal distribution from a sample standard deviation. Many other statistical tests also use this distribution, like Friedman's analysis of variance by ranks.

The chi-square distribution is a special case of the gamma distribution.

Definition

If Z₁, ..., Z_k are independent, standard normal random variables, then the sum of their squares,

$Q\ =\sum _{i=1}^{k}Z_{i}^{2},$

is distributed according to the chi-square distribution with k degrees of freedom. This is usually denoted as

$Q\ \sim \ \chi ^{2}(k)\ \ {\text{or}}\ \ Q\ \sim \ \chi _{k}^{2}.$

The chi-square distribution has one parameter: k — a positive integer that specifies the number of degrees of freedom (i.e. the number of Z_i’s)

Characteristics

Further properties of the chi-square distribution can be found in the box at right.

Probability density function

The probability density function (pdf) of the chi-square distribution is

$f(x;\,k)={\begin{cases}{\frac {1}{2^{k/2}\Gamma (k/2)}}\,x^{k/2-1}e^{-x/2},&x\geq 0;\\0,&{\text{otherwise}}.\end{cases}}$

where Γ(k/2) denotes the Gamma function, which has closed-form values at the half-integers.

For derivations of the pdf in the cases of one and two degrees of freedom, see Proofs related to chi-square distribution.

Cumulative distribution function

Its cumulative distribution function is:

$F(x;\,k)={\frac {\gamma (k/2,\,x/2)}{\Gamma (k/2)}}=P(k/2,\,x/2),$

where γ(k,z) is the lower incomplete Gamma function and P(k,z) is the regularized Gamma function.

In a special case of k = 2 this function has a simple form:

$F(x;\,2)=1-e^{-{\frac {x}{2}}}.$

This tables of distribution — usually in its cumulative form — are widely available and the function is included in many spreadsheets and all statistical packages. For a closed form approximation for the CDF, see under Noncentral chi-square distribution.

Additivity

It follows from the definition of the chi-square distribution that the sum of independent chi-square variables is also chi-square distributed. Specifically, if {X_i}_i=1ⁿ are independent chi-square variables with {k_i}_i=1ⁿ degrees of freedom, respectively, then Y = X₁ + ⋯ + X_n is chi-square distributed with k₁ + ⋯ + k_n degrees of freedom.

Information entropy

The information entropy is given by

$H=\int _{-\infty }^{\infty }f(x;\,k)\ln f(x;\,k)\,dx={\frac {k}{2}}+\ln {\big (}2\Gamma (k/2){\big )}+{\big (}1-k/2{\big )}\psi (k/2),$

where ψ(x) is the Digamma function.

Noncentral moments

The moments about zero of a chi-square distribution with k degrees of freedom are given by

$\operatorname {E} (X^{m})=k(k+2)(k+4)\cdots (k+2m-2)=2^{m}{\frac {\Gamma (m+k/2)}{\Gamma (k/2)}}.$

Cumulants

The cumulants are readily obtained by a (formal) power series expansion of the logarithm of the characteristic function:

$\kappa _{n}=2^{n-1}(n-1)!\,k$

Asymptotic properties

By the central limit theorem, because the chi-square distribution is the sum of k independent random variables with finite mean and variance, it converges to a normal distribution for large k (k > 50 is “approximately normal”). Specifically, if X ~ χ²(k), then as k tends to infinity, the distribution of $(X-k)/{\sqrt {2k}}$ tends to a standard normal distribution. However, convergence is slow as the skewness is ${\sqrt {8/k}}$ and the excess kurtosis is 12/k.

Other functions of the chi-square distribution converge more rapidly to a normal distribution. Some examples are:

• If X ~ χ²(k) then $\scriptstyle {\sqrt {2X}}$ is approximately normally distributed with mean $\scriptstyle {\sqrt {2k-1}}$ and unit variance (result credited to R. A. Fisher).
• If X ~ χ²(k) then $\scriptstyle {\sqrt[{3}]{X/k}}$ is approximately normally distributed with mean $\scriptstyle 1-2/(9k)$ and variance $\scriptstyle 2/(9k)$ (Wilson and Hilferty, 1931)

Related distributions

A chi-square variable with k degrees of freedom is defined as the sum of the squares of k independent standard normal random variables.

If Y is a k-dimensional Gaussian random vector with mean vector μ and rank k covariance matrix C, then X = (Y−μ)^TC⁻¹(Y−μ) is chi-square distributed with k degrees of freedom.

The sum of squares of statistically independent unit-variance Gaussian variables which do not have mean zero yields a generalization of the chi-square distribution called the noncentral chi-square distribution.

If Y is a vector of k i.i.d. standard normal random variables and A is a k×k idempotent matrix with rank k−n then the quadratic form Y^TAY is chi-square distributed with k−n degrees of freedom.

The chi-square distribution is also naturally related to other distributions arising from the Gaussian. In particular,

• Y is F-distributed, Y ~ F(k₁,k₂) if $\scriptstyle Y={\frac {X_{1}/k_{1}}{X_{2}/k_{2}}}$ where X₁ ~ χ²(k₁) and X₂  ~ χ²(k₂) are statistically independent.

• If X is chi-square distributed, then $\scriptstyle {\sqrt {X}}$ is chi distributed.

• If X₁  ~  χ²_k1 and X₂  ~  χ²_k2 are statistically independent, then X₁ + X₂  ~ χ²_k1+k2. If X₁ and X₂ are not independent, then X₁ + X₂ is not chi-square distributed.

Generalizations

The chi-square distribution is obtained as the sum of the squares of k independent, zero-mean, unit-variance Gaussian random variables. Generalizations of this distribution can be obtained by summing the squares of other types of Gaussian random variables. Several such distributions are described below.

Chi-square distributions

Noncentral chi-square distribution

Main article: Noncentral chi-square distribution

The noncentral chi-square distribution is obtained from the sum of the squares of independent Gaussian random variables having unit variance and nonzero means.

Generalized chi-square distribution

Main article: Generalized chi-square distribution

The generalized chi-square distribution is obtained from the quadratic form z′Az where z is a zero-mean Gaussian vector having an arbitrary covariance matrix, and A is an arbitrary matrix.

Gamma, exponential, and related distributions

The chi-square distribution X ~ χ²(k) is a special case of the gamma distribution, in that X ~ Γ(k/2, 2) (using the shape parameterization of the gamma distribution).

Because the exponential distribution is also a special case of the Gamma distribution, we also have that if X ~ χ²(2), then X ~ Exp(1/2) is an exponential distribution.

The Erlang distribution is also a special case of the Gamma distribution and thus we also have that if X ~ χ²(k) with even k, then X is Erlang distributed with shape parameter k/2 and scale parameter 1/2.

Applications

The chi-square distribution has numerous applications in inferential statistics, for instance in chi-square tests and in estimating variances. It enters the problem of estimating the mean of a normally distributed population and the problem of estimating the slope of a regression line via its role in Student’s t-distribution. It enters all analysis of variance problems via its role in the F-distribution, which is the distribution of the ratio of two independent chi-squared random variables divided by their respective degrees of freedom.

Following are some of the most common situations in which the chi-square distribution arises from a Gaussian-distributed sample.

• if X₁, ..., X_n are i.i.d. N(μ, σ²) random variables, then $\sum _{i=1}^{n}(X_{i}-{\bar {X}})^{2}\sim \sigma ^{2}\chi ^{2}(n-1)$ where ${\bar {X}}={\frac {1}{n}}\sum _{i=1}^{n}X_{i}$.

• The box below shows probability distributions with name starting with chi for some statistics based on X_i ∼ Normal(μ_i, σ²_i), i = 1, ⋯, k, independent random variables:

Name	Statistic
chi-square distribution	$\sum _{i=1}^{k}\left({\frac {X_{i}-\mu _{i}}{\sigma _{i}}}\right)^{2}$
noncentral chi-square distribution	$\sum _{i=1}^{k}\left({\frac {X_{i}}{\sigma _{i}}}\right)^{2}$
chi distribution	${\sqrt {\sum _{i=1}^{k}\left({\frac {X_{i}-\mu _{i}}{\sigma _{i}}}\right)^{2}}}$
noncentral chi distribution	${\sqrt {\sum _{i=1}^{k}\left({\frac {X_{i}}{\sigma _{i}}}\right)^{2}}}$

Table of χ² value vs P value

The P-value is the probability of observing a test statistic at least as extreme in a Chi-square distribution. Accordingly, since the cumulative distribution function (CDF) for the appropriate degrees of freedom (df) gives the probability of having obtained a value less extreme than this point, subtracting the CDF value from 1 gives the P-value. The table below gives a number of P-values matching to χ² for the first 10 degrees of freedom. A P-value of 0.05 or less is usually regarded as statistically significant.

Degrees of freedom (df)	χ² value
1	0.004	0.02	0.06	0.15	0.46	1.07	1.64	2.71	3.84	6.64	10.83
2	0.10	0.21	0.45	0.71	1.39	2.41	3.22	4.60	5.99	9.21	13.82
3	0.35	0.58	1.01	1.42	2.37	3.66	4.64	6.25	7.82	11.34	16.27
4	0.71	1.06	1.65	2.20	3.36	4.88	5.99	7.78	9.49	13.28	18.47
5	1.14	1.61	2.34	3.00	4.35	6.06	7.29	9.24	11.07	15.09	20.52
6	1.63	2.20	3.07	3.83	5.35	7.23	8.56	10.64	12.59	16.81	22.46
7	2.17	2.83	3.82	4.67	6.35	8.38	9.80	12.02	14.07	18.48	24.32
8	2.73	3.49	4.59	5.53	7.34	9.52	11.03	13.36	15.51	20.09	26.12
9	3.32	4.17	5.38	6.39	8.34	10.66	12.24	14.68	16.92	21.67	27.88
10	3.94	4.86	6.18	7.27	9.34	11.78	13.44	15.99	18.31	23.21	29.59
P value (Probability)	0.95	0.90	0.80	0.70	0.50	0.30	0.20	0.10	0.05	0.01	0.001
	Nonsignificant								Significant

See also

• Cochran's theorem
• Degrees of freedom (statistics)
• Fisher's method for combining independent tests of significance
• Generalized chi-square distribution
• High-dimensional space
• Inverse-chi-square distribution
• Noncentral chi-square distribution
• Normal distribution
• Pearson's chi-square test
• Proofs related to chi-square distribution
• Wishart distribution

References

Notations

• Wilson, E.B. Hilferty, M.M. (1931) The distribution of chi-square. Proceedings of the National Academy of Sciences, Washington, 17, 684–688.

External links

• Earliest Uses of Some of the Words of Mathematics: entry on Chi square has a brief history
• Course notes on Chi-Square Goodness of Fit Testing from Yale University Stats 101 class.
• Mathematica demonstration showing the chi-squared sampling distribution of various statistics, e.g. Σx², for a normal population
• Simple algorithm for approximating cdf and inverse cdf for the chi-square distribution with a pocket calculator