Beta prime distribution

Beta prime

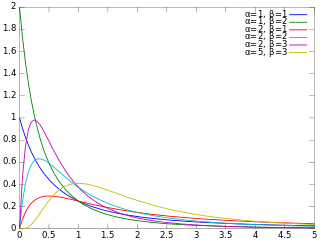
Probability density function
Cumulative distribution function
Parameters	$\alpha >0$ shape (real) $\beta >0$ shape (real)
Support	$x\in [0,\infty )\!$
PDF	$f(x)={\frac {x^{\alpha -1}(1+x)^{-\alpha -\beta }}{\mathrm {B} (\alpha ,\beta )}}\!$
CDF	$I_{{\frac {x}{1+x}}(\alpha ,\beta )}$ where $I_{x}(\alpha ,\beta )$ is the incomplete beta function
Mean	${\frac {\alpha }{\beta -1}}$ if $\beta >1$
Mode	${\frac {\alpha -1}{\beta +1}}{\text{ if }}\alpha \geq 1{\text{, 0 otherwise}}\!$
Variance	${\frac {\alpha (\alpha +\beta -1)}{(\beta -2)(\beta -1)^{2}}}$ if $\beta >2$
Skewness	${\frac {2(2\alpha +\beta -1)}{\beta -3}}{\sqrt {\frac {\beta -2}{\alpha (\alpha +\beta -1)}}}$ if $\beta >3$
Excess kurtosis	$6{\frac {\alpha (\alpha +\beta -1)(5\beta -11)+(\beta -1)^{2}(\beta -2)}{\alpha (\alpha +\beta -1)(\beta -3)(\beta -4)}}$ if $\beta >4$
Entropy	${\begin{aligned}&\log \left(\mathrm {B} (\alpha ,\beta )\right)+(\alpha -1)(\psi (\beta )-\psi (\alpha ))\\+&(\alpha +\beta )\left(\psi (1-\alpha -\beta )-\psi (1-\beta )+{\frac {\pi \sin(\alpha \pi )}{\sin(\beta \pi )\sin((\alpha +\beta )\pi ))}}\right)\end{aligned}}$ where $\psi$ is the digamma function.
MGF	Does not exist
CF	${\frac {e^{-it}\Gamma (\alpha +\beta )}{\Gamma (\beta )}}G_{1,2}^{\,2,0}\!\left(\left.{\begin{matrix}\alpha +\beta \\\beta ,0\end{matrix}}\;\right|\,-it\right)$

In probability theory and statistics, the beta prime distribution (also known as inverted beta distribution or beta distribution of the second kind) is an absolutely continuous probability distribution. If $p\in [0,1]$ has a beta distribution, then the odds ${\frac {p}{1-p}}$ has a beta prime distribution.

Definitions

Beta prime distribution is defined for $x>0$ with two parameters α and β, having the probability density function:

$f(x)={\frac {x^{\alpha -1}(1+x)^{-\alpha -\beta }}{\mathrm {B} (\alpha ,\beta )}}$

where B is the Beta function.

The cumulative distribution function is

$F(x;\alpha ,\beta )=I_{\frac {x}{1+x}}\left(\alpha ,\beta \right),$

where I is the regularized incomplete beta function.

While the related beta distribution is the conjugate prior distribution of the parameter of a Bernoulli distribution expressed as a probability, the beta prime distribution is the conjugate prior distribution of the parameter of a Bernoulli distribution expressed in odds. The distribution is a Pearson type VI distribution.

The mode of a variate X distributed as $\beta '(\alpha ,\beta )$ is ${\hat {X}}={\frac {\alpha -1}{\beta +1}}$. Its mean is ${\frac {\alpha }{\beta -1}}$ if $\beta >1$ (if $\beta \leq 1$ the mean is infinite, in other words it has no well defined mean) and its variance is ${\frac {\alpha (\alpha +\beta -1)}{(\beta -2)(\beta -1)^{2}}}$ if $\beta >2$.

For $-\alpha <k<\beta$, the k-th moment $E[X^{k}]$ is given by

$E[X^{k}]={\frac {\mathrm {B} (\alpha +k,\beta -k)}{\mathrm {B} (\alpha ,\beta )}}.$

For $k\in \mathbb {N}$ with $k<\beta ,$ this simplifies to

$E[X^{k}]=\prod _{i=1}^{k}{\frac {\alpha +i-1}{\beta -i}}.$

The cdf can also be written as

${\frac {x^{\alpha }\cdot {}_{2}F_{1}(\alpha ,\alpha +\beta ,\alpha +1,-x)}{\alpha \cdot \mathrm {B} (\alpha ,\beta )}}$

where ${}_{2}F_{1}$ is the Gauss's hypergeometric function ₂F₁ .

Alternative parameterization

The beta prime distribution may also be reparameterized in terms of its mean μ > 0 and precision ν > 0 parameters ( p. 36).

Consider the parameterization μ = α/(β − 1) and ν = β − 2, i.e., α = μ(1 + ν) and β = 2 + ν. Under this parameterization E[Y] = μ and Var[Y] = μ(1 + μ)/ν.

Generalization

Two more parameters can be added to form the generalized beta prime distribution $\beta '(\alpha ,\beta ,p,q)$:

• $p>0$ shape (real)
• $q>0$ scale (real)

having the probability density function:

$f(x;\alpha ,\beta ,p,q)={\frac {p\left({\frac {x}{q}}\right)^{\alpha p-1}\left(1+\left({\frac {x}{q}}\right)^{p}\right)^{-\alpha -\beta }}{q\mathrm {B} (\alpha ,\beta )}}$

with mean

${\frac {q\Gamma \left(\alpha +{\tfrac {1}{p}}\right)\Gamma (\beta -{\tfrac {1}{p}})}{\Gamma (\alpha )\Gamma (\beta )}}\quad {\text{if }}\beta p>1$

and mode

$q\left({\frac {\alpha p-1}{\beta p+1}}\right)^{\tfrac {1}{p}}\quad {\text{if }}\alpha p\geq 1$

Note that if p = q = 1 then the generalized beta prime distribution reduces to the standard beta prime distribution.

This generalization can be obtained via the following invertible transformation. If $y\sim \beta '(\alpha ,\beta )$ and $x=qy^{1/p}$ for $q,p>0$, then $x\sim \beta '(\alpha ,\beta ,p,q)$.

Compound gamma distribution

The compound gamma distribution is the generalization of the beta prime when the scale parameter, q is added, but where p = 1. It is so named because it is formed by compounding two gamma distributions:

$\beta '(x;\alpha ,\beta ,1,q)=\int _{0}^{\infty }G(x;\alpha ,r)G(r;\beta ,q)\;dr$

where $G(x;a,b)$ is the gamma pdf with shape $a$ and inverse scale $b$.

The mode, mean and variance of the compound gamma can be obtained by multiplying the mode and mean in the above infobox by q and the variance by q².

Another way to express the compounding is if $r\sim G(\beta ,q)$ and $x\mid r\sim G(\alpha ,r)$, then $x\sim \beta '(\alpha ,\beta ,1,q)$. This gives one way to generate random variates with compound gamma, or beta prime distributions. Another is via the ratio of independent gamma variates, as shown below.

Properties

• If $X\sim \beta '(\alpha ,\beta )$ then ${\tfrac {1}{X}}\sim \beta '(\beta ,\alpha )$.
• If $Y\sim \beta '(\alpha ,\beta )$, and $X=qY^{1/p}$, then $X\sim \beta '(\alpha ,\beta ,p,q)$.
• If $X\sim \beta '(\alpha ,\beta ,p,q)$ then $kX\sim \beta '(\alpha ,\beta ,p,kq)$.
• $\beta '(\alpha ,\beta ,1,1)=\beta '(\alpha ,\beta )$

Related distributions

• If $X\sim {\textrm {Beta}}(\alpha ,\beta )$, then ${\frac {X}{1-X}}\sim \beta '(\alpha ,\beta )$. This property can be used to generate beta prime distributed variates.
• If $X\sim \beta '(\alpha ,\beta )$, then ${\frac {X}{1+X}}\sim {\textrm {Beta}}(\alpha ,\beta )$. This is a corollary from the property above.
• If $X\sim F(2\alpha ,2\beta )$ has an F-distribution, then ${\tfrac {\alpha }{\beta }}X\sim \beta '(\alpha ,\beta )$, or equivalently, $X\sim \beta '(\alpha ,\beta ,1,{\tfrac {\beta }{\alpha }})$.
• For gamma distribution parametrization I:
  • If $X_{k}\sim \Gamma (\alpha _{k},\theta _{k})$ are independent, then ${\tfrac {X_{1}}{X_{2}}}\sim \beta '(\alpha _{1},\alpha _{2},1,{\tfrac {\theta _{1}}{\theta _{2}}})$. Note $\alpha _{1},\alpha _{2},{\tfrac {\theta _{1}}{\theta _{2}}}$ are all scale parameters for their respective distributions.
• For gamma distribution parametrization II:
  • If $X_{k}\sim \Gamma (\alpha _{k},\beta _{k})$ are independent, then ${\tfrac {X_{1}}{X_{2}}}\sim \beta '(\alpha _{1},\alpha _{2},1,{\tfrac {\beta _{2}}{\beta _{1}}})$. The $\beta _{k}$ are rate parameters, while ${\tfrac {\beta _{2}}{\beta _{1}}}$ is a scale parameter.
  • If $\beta _{2}\sim \Gamma (\alpha _{1},\beta _{1})$ and $X_{2}\mid \beta _{2}\sim \Gamma (\alpha _{2},\beta _{2})$, then $X_{2}\sim \beta '(\alpha _{2},\alpha _{1},1,\beta _{1})$. The $\beta _{k}$ are rate parameters for the gamma distributions, but $\beta _{1}$ is the scale parameter for the beta prime.
• $\beta '(p,1,a,b)={\textrm {Dagum}}(p,a,b)$ the Dagum distribution
• $\beta '(1,p,a,b)={\textrm {SinghMaddala}}(p,a,b)$ the Singh–Maddala distribution.
• $\beta '(1,1,\gamma ,\sigma )={\textrm {LL}}(\gamma ,\sigma )$ the log logistic distribution.
• The beta prime distribution is a special case of the type 6 Pearson distribution.
• If X has a Pareto distribution with minimum $x_{m}$ and shape parameter $\alpha$, then ${\dfrac {X}{x_{m}}}-1\sim \beta ^{\prime }(1,\alpha )$.
• If X has a Lomax distribution, also known as a Pareto Type II distribution, with shape parameter $\alpha$ and scale parameter $\lambda$, then ${\frac {X}{\lambda }}\sim \beta ^{\prime }(1,\alpha )$.
• If X has a standard Pareto Type IV distribution with shape parameter $\alpha$ and inequality parameter $\gamma$, then $X^{\frac {1}{\gamma }}\sim \beta ^{\prime }(1,\alpha )$, or equivalently, $X\sim \beta ^{\prime }(1,\alpha ,{\tfrac {1}{\gamma }},1)$.
• The inverted Dirichlet distribution is a generalization of the beta prime distribution.
• If $X\sim \beta '(\alpha ,\beta )$, then $\ln X$ has a generalized logistic distribution. More generally, if $X\sim \beta '(\alpha ,\beta ,p,q)$, then $\ln X$ has a scaled and shifted generalized logistic distribution.
• If $X\sim \beta '\left({\frac {1}{2}},{\frac {1}{2}}\right)$, then $\pm {\sqrt {X}}$ follows a Cauchy distribution, which is equivalent to a student-t distribution with the degrees of freedom of 1.

References

• Johnson, N.L., Kotz, S., Balakrishnan, N. (1995). Continuous Univariate Distributions, Volume 2 (2nd Edition), Wiley. ISBN 0-471-58494-0
• Bourguignon, M.; Santos-Neto, M.; de Castro, M. (2021), "A new regression model for positive random variables with skewed and long tail", Metron, 79: 33–55, doi:10.1007/s40300-021-00203-y, S2CID 233534544

• MathWorld article