Directed graph

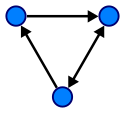
A directed graph.

A directed graph or digraph is a pair $G=(V,A)$ (sometimes $G=(V,E)$) of:

• a set V, whose elements are called vertices or nodes,
• a set A of ordered pairs of vertices, called arcs, directed edges, or arrows (and sometimes simply edges with the corresponding set named E instead of A).

It differs from an ordinary or undirected graph, in that the latter is defined in terms of unordered pairs of vertices, which are usually called edges.

Sometimes a digraph is called a simple digraph to distinguish it from a directed multigraph, in which the arcs constitute a multiset, rather than a set, of ordered pairs of vertices. Also, in a simple digraph loops are disallowed. (A loop is an arc that pairs a vertex to itself.) On the other hand, some texts allow loops, multiple arcs, or both in a digraph.

Basic terminology

An arc $e=(x,y)$ is considered to be directed from $x$ to $y$; $x$ is called the head and $y$ is called the tail of the arc; $y$ is said to be a direct successor of $x$, and $x$ is said to be a direct predecessor of $y$. If a path made up of one or more successive arcs leads from $x$ to $y$, then $y$ is said to be a successor of $x$, and $x$ is said to be a predecessor of $y$. The arc $(y,x)$ is called the arc $(x,y)$ inverted.

A directed graph G is called symmetric if, for every arc that belongs to G, the corresponding inverted arc also belongs to G. A symmetric loopless directed graph is equivalent to an undirected graph with the pairs of inverted arcs replaced with edges; thus the number of edges is equal to the number of arcs halved.

An orientation of a simple undirected graph is obtained by assigning a direction to each edge. Any directed graph constructed this way is called an oriented graph. A distinction between a simple directed graph and an oriented graph is that if $x$ and $y$ are vertices, a simple directed graph allows both $(x,y)$ and $(y,x)$ as edges, while only one is permitted in an oriented graph.

A weighted digraph is a digraph with weights assigned for its arcs, similarly to the weighted graph. A digraph with weighted edges in the context of graph theory is called a network.

The adjacency matrix of a digraph (with loops and multiple arcs) is the integer-valued matrix with rows and columns corresponding to the digraph nodes, where a nondiagonal entry $a_{ij}$ is the number of arcs from node i to node j, and the diagonal entry $a_{ii}$ is the number of loops at node i. The adjacency matrix for a digraph is unique up to the permutations of rows and columns.

Another matrix representation for a digraph is its incidence matrix.

See Glossary of graph theory#Direction for more definitions.

Indegree and outdegree

A digraph with vertices labeled (indegree, outdegree)

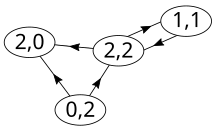
For a node, the number of head endpoints adjacent to a node is called the indegree of the node and the number of tail endpoints is its outdegree.

The indegree is denoted $\deg ^{-}(v)$ and the outdegree as $\deg ^{+}(v).$ A vertex with $\deg ^{-}(v)=0$ is called a source, as it is the origin of each of its incident edges. Similarly, a vertex with $\deg ^{+}(v)=0$ is called a sink.

The degree sum formula states that, for a directed graph

$\sum _{v\in V}\deg ^{+}(v)=\sum _{v\in V}\deg ^{-}(v)=|A|\,.$

If for every node, v ∈ V, $\deg ^{+}(v)=\deg ^{-}(v)$, the graph is called a balanced digraph.

Digraph connectivity

Main article: Connectivity (graph theory)

A digraph G is called weakly connected (or just connected) if the undirected underlying graph obtained by replacing all directed edges of G with undirected edges is a connected graph. A digraph is strongly connected or strong if it contains a directed path from u to v and a directed path from v to u for every pair of vertices u,v. The strong components are the maximal strongly connected subgraphs.

Classes of digraphs

A simple directed acyclic graph

An acyclic digraph (occasionally called a dag or DAG for "directed acyclic graph", although it is not the same as an orientation of an acyclic graph) is a directed graph with no directed cycles.

A rooted tree naturally defines an acyclic digraph, if all edges of the underlying tree are directed away from the root.

A tournament on 4 vertices

A tournament is an oriented graph obtained by choosing a direction for each edge in an undirected complete graph.

In the theory of Lie groups, a quiver Q is a directed graph serving as the domain of, and thus characterizing the shape of, a representation V defined as a functor, specifically an object of the functor category FinVct_K^F(Q) where F(Q) is the free category on Q consisting of paths in Q and FinVct_K is the category of finite dimensional vector spaces over a field K. Representations of a quiver label its vertices with vector spaces and its edges (and hence paths) compatibly with linear transformations between them, and transform via natural transformations.

See also

• Transpose graph
• Vertical constraint graph

References

• Bang-Jensen, Jørgen; Gutin, Gregory (2000), Digraphs: Theory, Algorithms and Applications, Springer, ISBN 1-85233-268-9
  (the corrected 1st edition of 2007 is now freely available on the authors' site; the 2nd edition appeared in 2009 ISBN 1848009976).
• Bondy, John Adrian; Murty, U. S. R. (1976), Graph Theory with Applications, North-Holland, ISBN 0-444-19451-7.
• Diestel, Reinhard (2005), Graph Theory (3rd ed.), Springer, ISBN 3-540-26182-6 (the electronic 3rd edition is freely available on author's site).
• Harary, Frank; Norman, Robert Z.; Cartwright, Dorwin (1965), Structural Models: An Introduction to the Theory of Directed Graphs, New York: Wiley.
• Number of directed graphs (or digraphs) with n nodes.