Möbius transformation

Möbius transformations should not be confused with the Möbius transform or the Möbius function.

In geometry, a Möbius transformation is a function:

$f(z)={\frac {az+b}{cz+d}}$

where z, a, b, c, d are complex numbers satisfying ad − bc ≠ 0.

Möbius transformations are named in honor of August Ferdinand Möbius, although they are also called homographic transformations or fractional linear transformations.

Overview

Möbius transformation is a bijective conformal map of the extended complex plane (i.e. the complex plane augmented by the point at infinity):

${\widehat {\mathbb {C} }}=\mathbb {C} \cup \{\infty \}.$

The set of all Möbius transformations forms a group under composition called the Möbius group.

The Möbius group is the automorphism group of the Riemann sphere, sometimes denoted

${\mbox{Aut}}({\widehat {\mathbb {C} }}).$

Certain subgroups of the Möbius group form the automorphism groups of the other simply-connected Riemann surfaces (the complex plane and the hyperbolic plane). As such, Möbius transformations play an important role in the theory of Riemann surfaces. The covering group of every Riemann surface is a discrete subgroup of the Möbius group (see Fuchsian group and Kleinian group). Möbius transformations are also closely related to isometries of hyperbolic 3-manifolds.

A particularly important subgroup of the Möbius group is the modular group; it is central to the theory of many fractals, modular forms, elliptic curves and Pellian equations.

In physics, the identity component of the Lorentz group acts on the celestial sphere the same way that the Möbius group acts on the Riemann sphere. In fact, these two groups are isomorphic. An observer who accelerates to relativistic velocities will see the pattern of constellations as seen near the Earth continuously transform according to infinitesimal Möbius transformations. This observation is often taken as the starting point of twistor theory.

Definition

The general form of a Möbius transformation is given by

$z\mapsto {\frac {az+b}{cz+d}}$

where a, b, c, d are any complex numbers satisfying ad − bc ≠ 0. This definition can be extended to the whole Riemann sphere (the complex plane plus the point at infinity).

The set of all Möbius transformations forms a group under composition. This group can be given the structure of a complex manifold in such a way that composition and inversion are holomorphic maps. The Möbius group is then a complex Lie group. The Möbius group is usually denoted ${\mbox{Aut}}({\widehat {\mathbb {C} }})$ as it is the automorphism group of the Riemann sphere.

Decomposition and Elementary properties

A mobius transformation is equivalent to a sequence of simpler transformations. Let:

* $f_{1}(z)=z+d/c$          (translation)
* $f_{2}(z)=1/z$            (inversion and reflection)
* $f_{3}(z)=-(ad-bc)/c^{2}\cdot z$      (dilation and rotation)
* $f_{4}(z)=z+a/c$         (translation)

then:

$f_{4}\circ f_{3}\circ f_{2}\circ f_{1}(z)={\frac {az+b}{cz+d}}$

This decompostion makes many properties of the mobius transform obvious.

For example, the preservation of angles is reduced to proving the angle preservation property of circle inversion, since all other transformation are isometries, which trivially preserve angles and distances.

The existence of an inverse mobius transformation function and its explicit formula is easily derived by a composition of the inverse function of the simpler transformations. That is, define functions g1, g2, g3, g4 such that g1 is the inverse of f1 and so on. Then, Composition[g1,g2,g3,g4][z] would be the explicit expression for the inverse mobius transformation, which is: (D Z - B)/(-C Z + A)

From this decomposition, we also see that mobius transformation carries over all non-trivial properties of circle inversion. Namely, that circles are mapped to circles, and angles are preserved. Also, because of the circle inversion, is carried over the convenience of defining möbius transformation over a plane with a point at infinity, which makes statements and concepts of möbius transformation's properties simpler.

For another example, look at f3. If A D - B C = 0, then the transformation collapses to the point 0, then f4 moves to A/C. Collapsing to a point is not an interesting transformation, thus we require in the definition of mobius transformation that $AD-BC\neq 0$.

Preservation of Angles and Circles

As seen from the above decomposition, mobius transformation contains this transformation 1/z, called complex inversion. Geometrically, a complex inversion is a circle inversion followed by a reflection around the x-axis.

In circle inversion, Circles are mapped to circles (here, lines are considered as circles with infinite radius), and angles are preserved. See circle inversion for various properties and proofs.

Cross-ratio preservation

The cross-ratio preservation theorem states that the cross-ratio

${\frac {(z_{1}-z_{3})(z_{2}-z_{4})}{(z_{1}-z_{4})(z_{2}-z_{3})}}={\frac {(w_{1}-w_{3})(w_{2}-w_{4})}{(w_{1}-w_{4})(w_{2}-w_{3})}}$

is invariant under a Möbius transformation that maps from z to w.

The action of the Möbius group on the Riemann sphere is sharply 3-transitive in the sense that there is a unique Möbius transformation which takes any three distinct points on the Riemann sphere to any other set of three distinct points. See the section below on specifying a transformation by three points.

Projective matrix representations

The transformation

$f(z)={\frac {az+b}{cz+d}}$

can be usefully expressed as a matrix

${\mathfrak {H}}={\begin{pmatrix}a&b\\c&d\end{pmatrix}}.$

The condition ad − bc ≠ 0 is equivalent to the condition that the determinant of above matrix be nonzero (i.e. the matrix should be non-singular). Note that multiplying ${\mathfrak {H}}$ by any complex number λ gives rise to the same transformation. Such matrix representations are called projective representations for reasons explained below. It is often convenient to normalize ${\mathfrak {H}}$ so that its determinant is equal to 1. The matrix ${\mathfrak {H}}$ is then unique up to sign.

The usefulness of this representation is that the composition of two Möbius transformations corresponds precisely to matrix multiplication of the corresponding matrices. That is, if we define a map

$\pi \colon {\mbox{GL}}(2,\mathbb {C} )\to {\mbox{Aut}}({\widehat {\mathbb {C} }})$

from the general linear group GL(2,C) to the Möbius group which sends the matrix ${\mathfrak {H}}$ to the transformation f, then this map is a group homomorphism.

The map $\pi$ is not an isomorphism, since it maps any scalar multiple of ${\mathfrak {H}}$ to the same transformation. The kernel of this homomorphism is then the set of all scalar matrices kI, which is the center of GL(2,C). The quotient group GL(2,C)/Z(GL(2,C)) is called the projective linear group and is usually denoted PGL(2,C). By the first isomorphism theorem of group theory we conclude that the Möbius group is isomorphic to PGL(2,C). Since Z(GL(2,C)) is the kernel of the group action given by GL(2,C) acting on itself by conjugation, PGL(2, C) is isomorphic to the inner automorphism group of GL(2,C). Moreover, the natural action of PGL(2,C) on the complex projective line CP¹ is exactly the natural action of the Möbius group on the Riemann sphere when the sphere and the projective line are identified as follows:

$[z_{1}:z_{2}]\leftrightarrow z_{1}/z_{2}.$

Here [z₁:z₂] are homogeneous coordinates on CP¹.

If one normalizes ${\mathfrak {H}}$ so that the determinant is equal to one, the map $\pi$ restricts to a surjective map from the special linear group SL(2,C) to the Möbius group. The Möbius group is therefore also isomorphic to PSL(2,C). We then have the following isomorphisms:

${\mbox{Aut}}({\widehat {\mathbb {C} }})\cong {\mbox{PGL}}(2,\mathbb {C} )\cong {\mbox{PSL}}(2,\mathbb {C} ).$

From the last identification we see that the Möbius group is a 3-dimensional complex Lie group (or a 6-dimensional real Lie group).

Note that there are precisely two matrices with unit determinant which can be used to represent any given Möbius transformation. That is, SL(2,C) is a double cover of PSL(2,C). Since SL(2,C) is simply-connected it is the universal cover of the Möbius group. The fundamental group of the Möbius group is then Z₂.

Classification

Möbius transformations are commonly classified into four types, parabolic, elliptic, hyperbolic and loxodromic (actually hyperbolic is a special case of loxodromic). The classification has both algebraic and geometric significance. Geometrically, the different types result in different transformations of the complex plane, as the figures below illustrate. These types can be distinguished by looking at the trace ${\mbox{tr}}\,{\mathfrak {H}}=a+d$. Note that the trace is invariant under conjugation, that is,

${\mbox{tr}}\,{\mathfrak {GHG}}^{-1}={\mbox{tr}}\,{\mathfrak {H}}$

and so every member of a conjugacy class will have the same trace. Every Möbius transformation can be written such that its representing matrix ${\mathfrak {H}}$ has determinant one (by multiplying the entries with a suitable scalar). Two Möbius transformations ${\mathfrak {H}},{\mathfrak {H}}'$ (both not equal to the identity transform) with $\det {\mathfrak {H}}=\det {\mathfrak {H}}'=1$ are conjugate if and only if ${\mbox{tr}}^{2}\,{\mathfrak {H}}={\mbox{tr}}^{2}\,{\mathfrak {H}}'$.

In the following discussion we will always assume that the representing matrix ${\mathfrak {H}}$ is normalized such that $\det {\mathfrak {H}}=ad-bc=1$.

Parabolic transforms The transform is said to be parabolic if

${\mbox{tr}}^{2}{\mathfrak {H}}=(a+d)^{2}=4$.

A transform is parabolic if and only if it has one fixed point in the compactified complex plane ${\widehat {\mathbb {C} }}=\mathbb {C} \cup \{\infty \}$. It is parabolic if and only if it is conjugate to

${\begin{pmatrix}1&1\\0&1\end{pmatrix}}$.

The subgroup consisting of all parabolic transforms of this form:

${\begin{pmatrix}1&b\\0&1\end{pmatrix}}$

is an example of a Borel subgroup, which generalizes the idea to higher dimensions.

All other non-identity transformations have two fixed points. All non-parabolic (non-identity) transforms are conjugate to

${\begin{pmatrix}\lambda &0\\0&\lambda ^{-1}\end{pmatrix}}$

with $\lambda$ not equal to 0,1 or -1. The square $k=\lambda ^{2}$ is called the characteristic constant or multiplier of the transformation.

Elliptic transforms The transform is said to be elliptic if

$0\leq {\mbox{tr}}^{2}{\mathfrak {H}}<4$.

A transform is elliptic if and only if $|\lambda |=1$. Writing $\lambda =e^{i\alpha }$, an elliptic transform is conjugate to

${\begin{pmatrix}\cos \alpha &\sin \alpha \\-\sin \alpha &\cos \alpha \end{pmatrix}}$

with $\alpha$ real. Note that for any ${\mathfrak {H}}$, the characteristic constant of ${\mathfrak {H}}^{n}$ is $k^{n}$. Thus, the only Möbius transformations of finite order are the elliptic transformations, and these only when λ is a root of unity; equivalently, when α is a rational multiple of pi.

Hyperbolic transforms The transform is said to be hyperbolic if

${\mbox{tr}}^{2}{\mathfrak {H}}>4$.

A transform is hyperbolic if and only if λ is real and positive.

Loxodromic transforms The transform is said to be loxodromic if ${\mbox{tr}}^{2}{\mathfrak {H}}$ is not in the closed interval of [0,4]. Hyperbolic transforms are thus a special case of loxodromic transformations. A transformation is loxodromic if and only if $|\lambda |\neq 1$. Historically, navigation by loxodrome or rhumb line refers to a path of constant bearing; the resulting path is a logarithmic spiral, similar in shape to the transformations of the complex plane that a loxodromic Möbius transformation makes. See the geometric figures below.

Transformation	Trace squared	Multipliers	Class representative
Elliptic	$0\leq \sigma <4$	$|k|=1$ $k=e^{\pm i\theta }\neq 1$	${\begin{pmatrix}e^{i\theta /2}&0\\0&e^{-i\theta /2}\end{pmatrix}}$	$z\mapsto e^{i\theta }z$
Parabolic	$\sigma =4$	$k=1$	${\begin{pmatrix}1&a\\0&1\end{pmatrix}}$	$z\mapsto z+a$
Hyperbolic	$4<\sigma <\infty$	$k\in \mathbb {R} ^{+}$ $k=e^{\pm \theta }\neq 1$	${\begin{pmatrix}e^{\theta /2}&0\\0&e^{-\theta /2}\end{pmatrix}}$	$z\mapsto e^{\theta }z$
Loxodromic	$\sigma \in \mathbb {C} ,\sigma \not \in [0,4]$	$|k|\neq 1$ $k=\lambda ^{2},\lambda ^{-2}$	${\begin{pmatrix}\lambda &0\\0&\lambda ^{-1}\end{pmatrix}}$	$z\mapsto kz$

Fixed points

Every non-identity Möbius transformation has two fixed points $\gamma _{1},\gamma _{2}$ on the Riemann sphere. Note that the fixed points are counted here with multiplicity; for parabolic transformations, the fixed points coincide. Either or both of these fixed points may be the point at infinity.

The fixed points of the transformation

$f(z)={\frac {az+b}{cz+d}}$

are obtained by solving the fixed point equation $f(\gamma )=\gamma$. For $c\neq 0$, this has two roots (proof):

$\gamma _{1,2}={\frac {(a-d)\pm {\sqrt {(a-d)^{2}+4bc}}}{2c}}={\frac {(a-d)\pm {\sqrt {(a+d)^{2}-4(ad-bc)}}}{2c}}.$

Note that for parabolic transformations, which satisfy $(a+d)^{2}=4(ad-bc)$, the fixed points coincide.

When $c=0$ one of the fixed points is at infinity, the other is given by

$\gamma =-{\frac {b}{a-d}}.$

The transformation will be a simple transformation composed of translations, rotations, and dilations: $z\mapsto \alpha z+\beta$.

If $c=0$ and $a=d$, then both fixed points are at infinity, and the Möbius transformation corresponds to a pure translation: $z\mapsto z+\beta$.

Normal form

Möbius transformations are also sometimes written in terms of their fixed points in so-called normal form. We first treat the non-parabolic case, for which there are two distinct fixed points.

Non-parabolic case:

Every non-parabolic transformation is conjugate to a dilation, i.e. a transformation of the form

$z\mapsto kz$

with fixed points at 0 and ∞. To see this define a map

$g(z)={\frac {z-\gamma _{1}}{z-\gamma _{2}}}$

which sends the points $(\gamma _{1},\gamma _{2})$ to $(0,\infty )$. Here we assume that both $\gamma _{1}$ and $\gamma _{2}$ are finite. If one of them is already at infinity then g can be modified so as to fix infinity and send the other point to 0.

If f has distinct fixed points $(\gamma _{1},\gamma _{2})$ then the transformation $gfg^{-1}$ has fixed points at 0 and ∞ and is therefore a dilation: $gfg^{-1}(z)=kz$. The fixed point equation for the transformation f can then be written

${\frac {f(z)-\gamma _{1}}{f(z)-\gamma _{2}}}=k{\frac {z-\gamma _{1}}{z-\gamma _{2}}}.$

Solving for f gives (in matrix form):

${\mathfrak {H}}(k;\gamma _{1},\gamma _{2})={\begin{pmatrix}\gamma _{1}-k\gamma _{2}&(k-1)\gamma _{1}\gamma _{2}\\1-k&k\gamma _{1}-\gamma _{2}\end{pmatrix}}$

or, if one of the fixed points is at infinity:

${\mathfrak {H}}(k;\gamma ,\infty )={\begin{pmatrix}k&(1-k)\gamma \\0&1\end{pmatrix}}$

From the above expressions one can calculate the derivatives of f at the fixed points:

$f'(\gamma _{1})=k\,$ and $f'(\gamma _{2})=1/k.\,$

Observe that, given an ordering of the fixed points, we can distinguish one of the multipliers (k) of f as the characteristic constant of f. Reversing the order of the fixed points is equivalent to taking the inverse multiplier for the characteristic constant:

${\mathfrak {H}}(k;\gamma _{1},\gamma _{2})={\mathfrak {H}}(1/k;\gamma _{2},\gamma _{1}).$

For loxodromic transformations, whenever $|k|>1$, one says that $\gamma _{1}$ is the repulsive fixed point, and $\gamma _{2}$ is the attractive fixed point. For $|k|<1$, the roles are reversed.

Parabolic case:

In the parabolic case there is only one fixed point $\gamma$. The transformation sending point to ∞ is

$g(z)={\frac {1}{z-\gamma }}$

or the identity if $\gamma$ is already at infinity. The transformation $gfg^{-1}$ fixes infinity and is therefore a translation:

$gfg^{-1}(z)=z+\beta \,.$

Here, β is called the translation length. The fixed point formula for a parabolic transformation is then

${\frac {1}{f(z)-\gamma }}={\frac {1}{z-\gamma }}+\beta$.

Solving for f (in matrix form) gives

${\mathfrak {H}}(\beta ;\gamma )={\begin{pmatrix}1+\gamma \beta &-\beta \gamma ^{2}\\\beta &1-\gamma \beta \end{pmatrix}}$

or, if $\gamma =\infty$:

${\mathfrak {H}}(\beta ;\infty )={\begin{pmatrix}1&\beta \\0&1\end{pmatrix}}$

Note that $\beta$ is not the characteristic constant of f, which is always 1 for a parabolic transformation. From the above expressions one can calculate:

$f'(\gamma )=1.\,$

Geometric interpretation of the characteristic constant

The following picture depicts (after stereographic transformation from the sphere to the plane) the two fixed points of a Möbius transformation in the non-parabolic case:

The characteristic constant can be expressed in terms of its logarithm:

$e^{\rho +\alpha i}=k\;$

When expressed in this way, the real number $\rho$ becomes an expansion factor. It indicates how repulsive the fixed point $\gamma _{1}$ is, and how attractive $\gamma _{2}$ is. The real number $\alpha$ is a rotation factor, indicating to what extent the transform rotates the plane anti-clockwise about $\gamma _{1}$ and clockwise about $\gamma _{2}$.

Elliptic transformations

If $\rho =0$, then the fixed points are neither attractive nor repulsive but indifferent, and the transformation is said to be elliptical. These transformations tend to move all points in circles around the two fixed points. If one of the fixed points is at infinity, this is equivalent to doing an affine rotation around a point.

If we take the one-parameter subgroup generated by any elliptic Möbius transformation, we obtain a continuous transformation, such that every transformation in the subgroup fixes the same two points. All other points flow along a family of circles which is nested between the two fixed points on the Riemann sphere. In general, the two fixed points can be any two distinct points.

This has an important physical interpretation. Imagine that some observer rotates with constant angular velocity about some axis. Then we can take the two fixed points to be the North and South poles of the celestial sphere. The appearance of the night sky is now transformed continuously in exactly the manner described by the one-parameter subgroup of elliptic transformations sharing the fixed points $0,\infty$, and with the number $\alpha$ corresponding to the constant angular velocity of our observer.

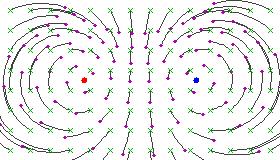
Here are some figures illustrating the effect of an elliptic Möbius transformation on the Riemann sphere (after stereographic projection to the plane):

These pictures illustrate the effect of a single Möbius transformation. The one-parameter subgroup which it generates continuously moves points along the family of circular arcs suggested by the pictures.

Hyperbolic transformations

If $\alpha$ is zero (or a multiple of $2\pi$), then the transformation is said to be hyperbolic. These transformations tend to move points along circular paths from one fixed point toward the other.

If we take the one-parameter subgroup generated by any hyperbolic Möbius transformation, we obtain a continuous transformation, such that every transformation in the subgroup fixes the same two points. All other points flow along a certain family of circular arcs away from the first fixed point and toward the second fixed point. In general, the two fixed points may be any two distinct points on the Riemann sphere.

This too has an important physical interpretation. Imagine that an observer accelerates (with constant magnitude of acceleration) in the direction of the North pole on his celestial sphere. Then the appearance of the night sky is transformed in exactly the manner described by the one-parameter subgroup of hyperbolic transformations sharing the fixed points $0,\infty$, with the real number $\rho$ corresponding to the magnitude of his acceleration vector. The stars seem to move along longitudes, away from the South pole toward the North pole. (The longitudes appear as circular arcs under stereographic projection from the sphere to the plane).

Here are some figures illustrating the effect of a hyperbolic Möbius transformation on the Riemann sphere (after stereographic projection to the plane):

It is not surprising that these pictures look very much like the field lines of bar magnets, since the circular flow lines subtend a constant angle between the two fixed points.

Loxodromic transformations

If both ρ and α are nonzero, then the transformation is said to be loxodromic. These transformations tend to move all points in S-shaped paths from one fixed point to the other.

The word "loxodrome" is from the Greek: "loxos, slanting + dromos, course". When sailing on a constant bearing - if you maintain a heading of (say) north-east, you will eventually wind up sailing around the north pole in a logarithmic spiral. On the mercator projection such a course is a straight line, as the north and south poles project to infinity. The angle that the loxodrome subtends relative to the lines of longitude (ie, its slope, the "tightness" of the spiral) is the argument of k. Of course, Möbius transformations may have their two fixed points anywhere, not just at the north and south poles. But any loxodromic transformation will be conjugate to a transform that moves all points along such loxodromes.

If we take the one-parameter subgroup generated by any loxodromic Möbius transformation, we obtain a continuous transformation, such that every transformation in the subgroup fixes the same two points. All other points flow along a certain family of curves, away from the first fixed point and toward the second fixed point. Unlike the hyperbolic case, these curves are not circular arcs, but certain curves which under stereographic projection from the sphere to the plane appear as spiral curves which twist counterclockwise infinitely often around one fixed point and twist clockwise infinitely often around the other fixed point. In general, the two fixed points may be any two distinct points on the Riemann sphere.

You can probably guess the physical interpretation in the case when the two fixed points are $0,\infty$: an observer who is both rotating (with constant angular velocity) about some axis and boosting (with constant magnitude acceleration) along the same axis, will see the appearance of the night sky transform according to the one-parameter subgroup of loxodromic transformations with fixed points $0,\infty$, and with $\rho ,\alpha$ determined respectively by the magnitude of acceleration and angular velocity.

Here are some pictures illustrating the effect of a loxodromic transformation:

Stereographic projection

These images show Möbius transformations stereographically projected onto the Riemann sphere. Note in particular that when projected onto a sphere, the special case of a fixed point at infinity looks no different to having the fixed points in an arbitrary location.

	Elliptic	Hyperbolic	Loxodromic
One fixed point at Infinity
	Full size	Full size	Full size
Fixed points diametrically opposite
	Full size	Full size	Full size
Fixed points in an arbitrary location
	Full size	Full size	Full size

Iterating a transformation

If a transformation ${\mathfrak {H}}$ has fixed points $\gamma _{1},\gamma _{2}$, and characteristic constant 'k, then ${\mathfrak {H}}'={\mathfrak {H}}^{n}$ will have $\gamma _{1}'=\gamma _{1},\gamma _{2}'=\gamma _{2},k'=k^{n}$.

This can be used to iterate a transformation, or to animate one by breaking it up into steps.

These images show three points (red, blue and black) continuously iterated under transformations with various characteristic constants.

Poles of the transformation

The point

$z_{\infty }=-{\frac {d}{c}}$

is called the pole of ${\mathfrak {H}}$; it is that point which is transformed to the point at infinity under ${\mathfrak {H}}$.

The inverse pole

$Z_{\infty }={\frac {a}{c}}$

Is that point to which the point at infinity is transformed. The point midway between the two poles is always the same as the point midway between the two fixed points:

$\gamma _{1}+\gamma _{2}=z_{\infty }+Z_{\infty }$

These four points are the vertices of a parallelogram which is sometimes called the characteristic parallelogram of the transformation.

A transform ${\mathfrak {H}}$ can be specified with two fixed points $\gamma _{1},\gamma _{2}$ and the pole $z_{\infty }$.

${\mathfrak {H}}={\begin{pmatrix}Z_{\infty }&-\gamma _{1}\gamma _{2}\\1&-z_{\infty }\end{pmatrix}},\;\;Z_{\infty }=\gamma _{1}+\gamma _{2}-z_{\infty }$

This allows us to derive a formula for conversion between $k$ and $z_{\infty }$ given $\gamma _{1},\gamma _{2}$:

$z_{\infty }={\frac {k\gamma _{1}-\gamma _{2}}{1-k}}$

$k={\frac {\gamma _{2}-z_{\infty }}{\gamma _{1}-z_{\infty }}}={\frac {Z_{\infty }-\gamma _{1}}{Z_{\infty }-\gamma _{2}}}={\frac {a-c\gamma _{1}}{a-c\gamma _{2}}}$

Which reduces down to

$k={\frac {(a+d)+{\sqrt {(a-d)^{2}+4bc}}}{(a+d)-{\sqrt {(a-d)^{2}+4bc}}}}$

The last expression coincides with one of the (mutually reciprocal) eigenvalue ratios $\lambda _{1} \over \lambda _{2}$ of the matrix

${\mathfrak {H}}={\begin{pmatrix}a&b\\c&d\end{pmatrix}}$

representing the transform (compare the discussion in the preceding section about the characteristic constant of a transformation). Its characteristic polynomial is equal to

${\mbox{det}}(\lambda I_{2}-{\mathfrak {H}})=\lambda ^{2}-{\mbox{tr}}{\mathfrak {H}}\,\lambda +{\mbox{det}}{\mathfrak {H}}=\lambda ^{2}-(a+d)\lambda +(ad-bc)$

which has roots

$\lambda _{i}={\frac {(a+d)\pm {\sqrt {(a-d)^{2}+4bc}}}{2}}={\frac {(a+d)\pm {\sqrt {(a+d)^{2}-4(ad-bc)}}}{2}}\ .$

Specifying a transformation by three points

Direct approach

Any set of three points

$Z_{1}={\mathfrak {H}}(z_{1}),\;\;Z_{2}={\mathfrak {H}}(z_{2}),\;\;Z_{3}={\mathfrak {H}}(z_{3})$

uniquely defines a transformation ${\mathfrak {H}}$. To calculate this out, it is handy to make use of a transformation that is able to map three points onto (0,0), (1, 0) and the point at infinity.

${\mathfrak {H}}_{1}={\begin{pmatrix}{\frac {z_{2}-z_{3}}{z_{2}-z_{1}}}&-z_{1}{\frac {z_{2}-z_{3}}{z_{2}-z_{1}}}\\1&-z_{3}\end{pmatrix}},\;\;{\mathfrak {H}}_{2}={\begin{pmatrix}{\frac {Z_{2}-Z_{3}}{Z_{2}-Z_{1}}}&-Z_{1}{\frac {Z_{2}-Z_{3}}{Z_{2}-Z_{1}}}\\1&-Z_{3}\end{pmatrix}}$

One can get rid of the infinities by multiplying out by $z_{2}-z_{1}$ and $Z_{2}-Z_{1}$ as previously noted.

${\mathfrak {H}}_{1}={\begin{pmatrix}z_{2}-z_{3}&z_{1}z_{3}-z_{1}z_{2}\\z_{2}-z_{1}&z_{1}z_{3}-z_{3}z_{2}\end{pmatrix}},\;\;{\mathfrak {H}}_{2}={\begin{pmatrix}Z_{2}-Z_{3}&Z_{1}Z_{3}-Z_{1}Z_{2}\\Z_{2}-Z_{1}&Z_{1}Z_{3}-Z_{3}Z_{2}\end{pmatrix}}$

The matrix ${\mathfrak {H}}$ to map $z_{1,2,3}$ onto $Z_{1,2,3}$ then becomes

${\mathfrak {H}}={\mathfrak {H}}_{2}^{-1}{\mathfrak {H}}_{1}$

You can multiply this out, if you want, but if you are writing code then it's easier to use temporary variables for the middle terms.

Explicit determinant formula

The problem of constructing a Möbius transformation ${\mathfrak {H}}(z)$ mapping a triple $(z_{1},z_{2},z_{3})$ to another triple $(w_{1},w_{2},w_{3})$ is equivalent to finding the equation of a standard hyperbola

$\,cwz-az+dw-b=0$

in the (z,w)-plane passing through the points $(z_{i},w_{i})$. An explicit equation can be found by evaluating the determinant

$\det {\begin{pmatrix}zw&z&w&1\\z_{1}w_{1}&z_{1}&w_{1}&1\\z_{2}w_{2}&z_{2}&w_{2}&1\\z_{3}w_{3}&z_{3}&w_{3}&1\end{pmatrix}}\,$

by means of a Laplace expansion along the first row. This results in the determinant formulae

$a=\det {\begin{pmatrix}z_{1}w_{1}&w_{1}&1\\z_{2}w_{2}&w_{2}&1\\z_{3}w_{3}&w_{3}&1\end{pmatrix}}\,$

$b=\det {\begin{pmatrix}z_{1}w_{1}&z_{1}&w_{1}\\z_{2}w_{2}&z_{2}&w_{2}\\z_{3}w_{3}&z_{3}&w_{3}\end{pmatrix}}\,$

$c=\det {\begin{pmatrix}z_{1}&w_{1}&1\\z_{2}&w_{2}&1\\z_{3}&w_{3}&1\end{pmatrix}}\,$

$d=\det {\begin{pmatrix}z_{1}w_{1}&z_{1}&1\\z_{2}w_{2}&z_{2}&1\\z_{3}w_{3}&z_{3}&1\end{pmatrix}}$

for the coefficients $a,b,c,d$ of the representing matrix $\,{\mathfrak {H}}={\begin{pmatrix}a&b\\c&d\end{pmatrix}}$. The constructed matrix ${\mathfrak {H}}$ has determinant equal to $(z_{1}-z_{2})(z_{1}-z_{3})(z_{2}-z_{3})(w_{1}-w_{2})(w_{1}-w_{3})(w_{2}-w_{3})$ which does not vanish if the z_i resp. w_i are pairwise different thus the Möbius transformation is well-defined.

Remark: A similar determinant (with $wz$ replaced by $w^{2}+z^{2}$) leads to the equation of a circle through three different (non collinear) points in the plane.

Alternate method using cross-ratios of point quadruples

This construction exploits the fact (mentioned in the first section) that the cross-ratio

${\mbox{cr}}(z_{1},z_{2},z_{3},z_{4})={{(z_{1}-z_{3})(z_{2}-z_{4})} \over {(z_{1}-z_{4})(z_{2}-z_{3})}}$

is invariant under a Möbius transformation mapping a quadruple $(z_{1},z_{2},z_{3},z_{4})$ to $(w_{1},w_{2},w_{3},w_{4})$ via $w_{i}={\mathfrak {H}}z_{i}$. If ${\mathfrak {H}}$ maps a triple $(z_{1},z_{2},z_{3})$ of pairwise different z_i to another triple $(w_{1},w_{2},w_{3})$, then the Möbius transformation ${\mathfrak {H}}$ is determined by the equation

${\mbox{cr}}({\mathfrak {H}}(z),w_{1},w_{2},w_{3})={\mbox{cr}}(z,z_{1},z_{2},z_{3})$

or written out in concrete terms:

${{({\mathfrak {H}}(z)-w_{2})(w_{1}-w_{3})} \over {({\mathfrak {H}}(z)-w_{3})(w_{1}-w_{2})}}={{(z-z_{2})(z_{1}-z_{3})} \over {(z-z_{3})(z_{1}-z_{2})}}\ .$

The last equation can be transformed into

${{{\mathfrak {H}}(z)-w_{2}} \over {{\mathfrak {H}}(z)-w_{3}}}={{(z-z_{2})(w_{1}-w_{2})(z_{1}-z_{3})} \over {(z-z_{3})(w_{1}-w_{3})(z_{1}-z_{2})}}\ .$

Solving this equation for ${\mathfrak {H}}(z)$ one obtains the sought transformation.

Relation to the fixed point normal form

Assume that the points $z_{2},\,z_{3}$ are the two (different) fixed points of the Möbius transform ${\mathfrak {H}}$ i.e. $w_{2}=z_{2},\,w_{3}=z_{3}$. Write $z_{2}=\gamma _{1},\,z_{3}=\gamma _{2}$. The last equation

${{{\mathfrak {H}}(z)-w_{2}} \over {{\mathfrak {H}}(z)-w_{3}}}={{(z-z_{2})(w_{1}-w_{2})(z_{1}-z_{3})} \over {(z-z_{3})(w_{1}-w_{3})(z_{1}-z_{2})}}$

then reads

${{{\mathfrak {H}}(z)-\gamma _{1}} \over {{\mathfrak {H}}(z)-\gamma _{2}}}={{(w_{1}-\gamma _{1})(z_{1}-\gamma _{2})} \over {(w_{1}-\gamma _{2})(z_{1}-\gamma _{1})}}\cdot {{z-\gamma _{1}} \over {z-\gamma _{2}}}\ .$

In the previous section on normal form a Möbius transform with two fixed points $\gamma _{1},\gamma _{2}$ was expressed using the characteristic constant k of the transform as

${{{\mathfrak {H}}(z)-\gamma _{1}} \over {{\mathfrak {H}}(z)-\gamma _{2}}}=k\,{{z-\gamma _{1}} \over {z-\gamma _{2}}}\ .$

Comparing both expressions one derives the equality

$k={{(w_{1}-\gamma _{1})(z_{1}-\gamma _{2})} \over {(w_{1}-\gamma _{2})(z_{1}-\gamma _{1})}}={\mbox{cr}}(w_{1},z_{1},\gamma _{1},\gamma _{2})\ ,$

where $z_{1}$ is different from the fixed points $\gamma _{1},\,\gamma _{2}$ and $w_{1}={\mathfrak {H}}(z_{1})$ is the image of z₁ under ${\mathfrak {H}}$. In particular the cross-ratio ${\mbox{cr}}({\mathfrak {H}}(z),z,\gamma _{1},\gamma _{2})$ does not depend on the choice of the point z (different from the two fixed points) and is equal to the characteristic constant.

See also

• Fuchsian group
• Hyperbolic geometry
• Inversive ring geometry
• Kleinian group
• Lorentz group
• Modular group
• Poincaré half-plane model
• Projective geometry
• Bilinear transform

References

• David Mumford, Caroline Series and David Wright (2002). Indra's Pearls; The Vision of Felix Klein. Cambridge University Press. ISBN 0-521-35253-3. (Aimed at non-mathematicians, provides an excellent exposition of theory and results, richly illustrated with diagrams.)

• Konrad Knopp (1952). Elements of the Theory of Functions. New York: Dover. ISBN 0-486-60154-4. (See Chapters 3-5 of this classic book for a beautiful introduction to the Riemann sphere, stereographic projection, and Möbius transformations.)

• Tristam Needham (1997). Visual Complex Analysis. Oxford: Clarendon Press. ISBN 0-19-853446-9. (See Chapter 3 for a beautifully illustrated introduction to Möbius transformations, including their classification up to conjugacy.)

• Alan F. Beardon (1995). The Geometry of Discrete Groups. New York: Springer-Verlag. ISBN 0-3879-0788-2.

• Svetlana Katok (1992). Fuchsian Groups. Chicago:University of Chicago Press. ISBN 0-226-42583-5. See Chapter 2.

• Gareth A. Jones and David Singerman (1987). Complex Functions: an Algebraic and Geometric Viewpoint. Cambridge: Cambridge Univerisy Press. ISBN 0-521-313666-X. (See Chapter 2 for various isomorphisms, and for the Lorentz group viewed as a Galois group.)

• G. S. Hall (2004). Symmetries and Curvature Structure in General Relativity. Singapore: World Scientific. ISBN 981-02-1051-5. (See Chapter 6 for the classification, up to conjugacy, of the Lie subalgebras of the Lie algebra of the Lorentz group.)

External links

• A java applet allowing you to specify a transformation via its fixed points and so on can be found at [1].

• conformal maps gallery [2]