6-orthoplex

6-orthoplex Hexacross
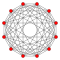
Orthogonal projection inside Petrie polygon
Type	Regular 6-polytope
Family	orthoplex
Schläfli symbols	{3,3,3,3,4} {3,3,3,31,1}
Coxeter-Dynkin diagrams	=
5-faces	64 {34}
4-faces	192 {33}
Cells	240 {3,3}
Faces	160 {3}
Edges	60
Vertices	12
Vertex figure	5-orthoplex
Petrie polygon	dodecagon
Coxeter groups	B6, [4,34] D6, [33,1,1]
Dual	6-cube
Properties	convex

In geometry, a 6-orthoplex, or 6-cross polytope, is a regular 6-polytope with 12 vertices, 60 edges, 160 triangle faces, 240 tetrahedron cells, 192 5-cell 4-faces, and 64 5-faces.

It has two constructed forms, the first being regular with Schläfli symbol {3⁴,4}, and the second with alternately labeled (checkerboarded) facets, with Schläfli symbol {3,3,3,3^1,1} or Coxeter symbol 3₁₁.

It is a part of an infinite family of polytopes, called cross-polytopes or orthoplexes. The dual polytope is the 6-hypercube, or hexeract.

Alternate names

• Hexacross, derived from combining the family name cross polytope with hex for six (dimensions) in Greek.
• Hexacontitetrapeton as a 64-facetted 6-polytope.

As a configuration

The elements of the regular polytopes can be expressed in a configuration matrix. Rows and columns reference vertices, edges, faces, and cells, with diagonal element their counts (f-vectors). The nondiagonal elements represent the number of row elements are incident to the column element. The configurations for dual polytopes can be seen by rotating the matrix elements by 180 degrees.

${\begin{bmatrix}{\begin{matrix}12&10&40&80&80&32\\2&60&8&24&32&16\\3&3&160&6&12&8\\4&6&4&240&4&4\\5&10&10&5&192&2\\6&15&20&15&6&64\end{matrix}}\end{bmatrix}}$

Construction

There are three Coxeter groups associated with the 6-orthoplex, one regular, dual of the hexeract with the C₆ or [4,3,3,3,3] Coxeter group, and a half symmetry with two copies of 5-simplex facets, alternating, with the D₆ or [3^3,1,1] Coxeter group. A lowest symmetry construction is based on a dual of a 6-orthotope, called a 6-fusil.

Name	Coxeter	Schläfli	Symmetry	Order
Regular 6-orthoplex		{3,3,3,3,4}	[4,3,3,3,3]	46080
Quasiregular 6-orthoplex		{3,3,3,31,1}	[3,3,3,31,1]	23040
6-fusil		{3,3,3,4}+{}	[4,3,3,3,3]	7680
		{3,3,4}+{4}	[4,3,3,2,4]	3072
		2{3,4}	[4,3,2,4,3]	2304
		{3,3,4}+2{}	[4,3,3,2,2]	1536
		{3,4}+{4}+{}	[4,3,2,4,2]	768
		3{4}	[4,2,4,2,4]	512
		{3,4}+3{}	[4,3,2,2,2]	384
		2{4}+2{}	[4,2,4,2,2]	256
		{4}+4{}	[4,2,2,2,2]	128
		6{}	[2,2,2,2,2]	64

Cartesian coordinates

Cartesian coordinates for the vertices of a 6-orthoplex, centered at the origin are

(±1,0,0,0,0,0), (0,±1,0,0,0,0), (0,0,±1,0,0,0), (0,0,0,±1,0,0), (0,0,0,0,±1,0), (0,0,0,0,0,±1)

Every vertex pair is connected by an edge, except opposites.

Images

orthographic projections

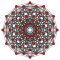
Coxeter plane	B6	B5	B4
Graph
Dihedral symmetry	[12]	[10]	[8]
Coxeter plane	B3	B2
Graph
Dihedral symmetry	[6]	[4]
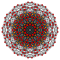
Coxeter plane	A5	A3
Graph
Dihedral symmetry	[6]	[4]

Related polytopes

The 6-orthoplex can be projected down to 3-dimensions into the vertices of a regular icosahedron.

2D		3D
Icosahedron {3,5} = H3 Coxeter plane	6-orthoplex {3,3,3,31,1} = D6 Coxeter plane	Icosahedron	6-orthoplex
This construction can be geometrically seen as the 12 vertices of the 6-orthoplex projected to 3 dimensions as the vertices of a regular icosahedron. This represents a geometric folding of the D6 to H3 Coxeter groups: : to . On the left, seen by these 2D Coxeter plane orthogonal projections, the two overlapping central vertices define the third axis in this mapping. Every pair of vertices of the 6-orthoplex are connected, except opposite ones: 30 edges are shared with the icosahedron, while 30 more edges from the 6-orthoplex project to the interior of the icosahedron.

It is in a dimensional series of uniform polytopes and honeycombs, expressed by Coxeter as 3_k1 series. (A degenerate 4-dimensional case exists as 3-sphere tiling, a tetrahedral hosohedron.)

3_k1 dimensional figures

Space	Finite				Euclidean	Hyperbolic
n	4	5	6	7	8	9
Coxeter group	A3A1	A5	D6	E7	${\tilde {E}}_{7}$=E7+	${\bar {T}}_{8}$=E7++
Coxeter diagram
Symmetry	[3−1,3,1]	[30,3,1]	[[31,3,1]] = [4,3,3,3,3]	[32,3,1]	[33,3,1]	[34,3,1]
Order	48	720	46,080	2,903,040	∞
Graph					-	-
Name	31,-1	310	311	321	331	341

This polytope is one of 63 uniform 6-polytopes generated from the B₆ Coxeter plane, including the regular 6-cube or 6-orthoplex.

References

• H.S.M. Coxeter:
  • H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
  • Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
    • (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
    • (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
    • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
• Norman Johnson Uniform Polytopes, Manuscript (1991)
  • N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. 1966
• Klitzing, Richard. "6D uniform polytopes (polypeta) x3o3o3o3o4o - gee".

Specific

External links

• Olshevsky, George. "Cross polytope". Glossary for Hyperspace. Archived from the original on 4 February 2007.
• Polytopes of Various Dimensions
• Multi-dimensional Glossary