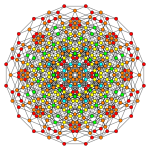
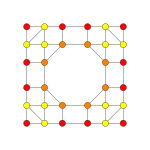From Wikipedia, the free encyclopedia
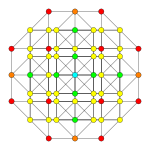
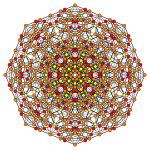
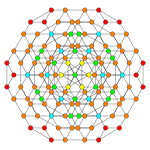
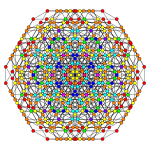
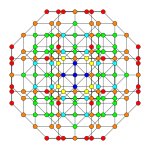
6-cube Stericated 6-cube Steritruncated 6-cube
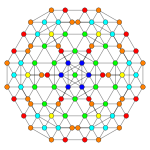
Stericantellated 6-cube Stericantitruncated 6-cube Steriruncinated 6-cube
Steriruncitruncated 6-cube Steriruncicantellated 6-cube Steriruncicantitruncated 6-cube
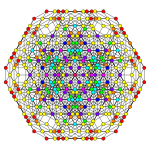
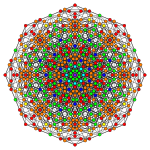
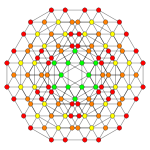
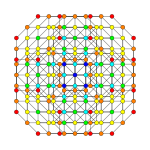
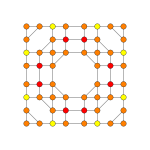
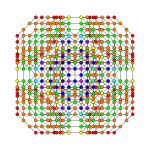
Orthogonal projections in B6 Coxeter plane
In six-dimensional geometry , a stericated 6-cube is a convex uniform 6-polytope , constructed as a sterication (4th order truncation) of the regular 6-cube .
There are 8 unique sterications for the 6-cube with permutations of truncations, cantellations, and runcinations.
Small cellated hexeract (Acronym: scox) (Jonathan Bowers)[ 1] Steritruncated 6-cube [ edit ]
Steritruncated 6-cube
Type
uniform 6-polytope
Schläfli symbol t0,1,4 {4,3,3,3,3}
Coxeter-Dynkin diagrams
5-faces
4-faces
Cells
Faces
Edges
19200
Vertices
3840
Vertex figure
Coxeter groups B6 , [4,3,3,3,3]
Properties
convex
Cellirhombated hexeract (Acronym: catax) (Jonathan Bowers)[ 2] Stericantellated 6-cube [ edit ] Cellirhombated hexeract (Acronym: crax) (Jonathan Bowers)[ 3] Stericantitruncated 6-cube [ edit ]
stericantitruncated 6-cube
Type
uniform 6-polytope
Schläfli symbol t0,1,2,4 {4,3,3,3,3}
Coxeter-Dynkin diagrams
5-faces
4-faces
Cells
Faces
Edges
46080
Vertices
11520
Vertex figure
Coxeter groups B6 , [4,3,3,3,3]
Properties
convex
Celligreatorhombated hexeract (Acronym: cagorx) (Jonathan Bowers)[ 4] Steriruncinated 6-cube [ edit ]
steriruncinated 6-cube
Type
uniform 6-polytope
Schläfli symbol t0,3,4 {4,3,3,3,3}
Coxeter-Dynkin diagrams
5-faces
4-faces
Cells
Faces
Edges
15360
Vertices
3840
Vertex figure
Coxeter groups B6 , [4,3,3,3,3]
Properties
convex
Celliprismated hexeract (Acronym: copox) (Jonathan Bowers)[ 5] Steriruncitruncated 6-cube [ edit ] Celliprismatotruncated hexeract (Acronym: captix) (Jonathan Bowers)[ 6] Steriruncicantellated 6-cube [ edit ]
steriruncicantellated 6-cube
Type
uniform 6-polytope
Schläfli symbol t0,2,3,4 {4,3,3,3,3}
Coxeter-Dynkin diagrams
5-faces
4-faces
Cells
Faces
Edges
40320
Vertices
11520
Vertex figure
Coxeter groups B6 , [4,3,3,3,3]
Properties
convex
Celliprismatorhombated hexeract (Acronym: coprix) (Jonathan Bowers)[ 7] Steriruncicantitruncated 6-cube [ edit ] Great cellated hexeract (Acronym: gocax) (Jonathan Bowers)[ 8] These polytopes are from a set of 63 uniform 6-polytopes generated from the B6 Coxeter plane , including the regular 6-cube or 6-orthoplex .
B6 polytopes
β6
t1 β6
t2 β6
t2 γ6
t1 γ6
γ6
t0,1 β6
t0,2 β6
t1,2 β6
t0,3 β6
t1,3 β6
t2,3 γ6
t0,4 β6
t1,4 γ6
t1,3 γ6
t1,2 γ6
t0,5 γ6
t0,4 γ6
t0,3 γ6
t0,2 γ6
t0,1 γ6
t0,1,2 β6
t0,1,3 β6
t0,2,3 β6
t1,2,3 β6
t0,1,4 β6
t0,2,4 β6
t1,2,4 β6
t0,3,4 β6
t1,2,4 γ6
t1,2,3 γ6
t0,1,5 β6
t0,2,5 β6
t0,3,4 γ6
t0,2,5 γ6
t0,2,4 γ6
t0,2,3 γ6
t0,1,5 γ6
t0,1,4 γ6
t0,1,3 γ6
t0,1,2 γ6
t0,1,2,3 β6
t0,1,2,4 β6
t0,1,3,4 β6
t0,2,3,4 β6
t1,2,3,4 γ6
t0,1,2,5 β6
t0,1,3,5 β6
t0,2,3,5 γ6
t0,2,3,4 γ6
t0,1,4,5 γ6
t0,1,3,5 γ6
t0,1,3,4 γ6
t0,1,2,5 γ6
t0,1,2,4 γ6
t0,1,2,3 γ6
t0,1,2,3,4 β6
t0,1,2,3,5 β6
t0,1,2,4,5 β6
t0,1,2,4,5 γ6
t0,1,2,3,5 γ6
t0,1,2,3,4 γ6
t0,1,2,3,4,5 γ6
^ Klitzing, (x4o3o3o3x3o - scox)
^ Klitzing, (x4x3o3o3x3o - catax)
^ Klitzing, (x4o3x3o3x3o - crax)
^ Klitzing, (x4x3x3o3x3o - cagorx)
^ Klitzing, (x4o3o3x3x3o - copox))
^ Klitzing, (x4x3o3x3x3o - captix)
^ Klitzing, (x4o3x3x3x3o - coprix)
^ Klitzing, (x4x3x3x3x3o - gocax)
H.S.M. Coxeter :
H.S.M. Coxeter, Regular Polytopes , 3rd Edition, Dover New York, 1973
Kaleidoscopes: Selected Writings of H.S.M. Coxeter , edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
(Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
(Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II , [Math. Zeit. 188 (1985) 559-591]
(Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III , [Math. Zeit. 200 (1988) 3-45] Norman Johnson Uniform Polytopes , Manuscript (1991)
N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs , Ph.D. Klitzing, Richard. "6D uniform polytopes (polypeta)" .