Beltrami identity

Eugenio Beltrami

The Beltrami identity, named after Eugenio Beltrami, is a special case of the Euler–Lagrange equation in the calculus of variations.

The Euler–Lagrange equation serves to extremize action functionals of the form

$I[u]=\int _{a}^{b}L[x,u(x),u'(x)]\,dx\,,$

where $a$ and $b$ are constants and $u'(x)={\frac {du}{dx}}$.

If ${\frac {\partial L}{\partial x}}=0$, then the Euler–Lagrange equation reduces to the Beltrami identity,

$L-u'{\frac {\partial L}{\partial u'}}=C\,,$

where C is a constant.

Derivation

The following derivation of the Beltrami identity starts with the Euler–Lagrange equation,

${\frac {\partial L}{\partial u}}={\frac {d}{dx}}{\frac {\partial L}{\partial u'}}\,.$

Multiplying both sides by u′,

$u'{\frac {\partial L}{\partial u}}=u'{\frac {d}{dx}}{\frac {\partial L}{\partial u'}}\,.$

According to the chain rule,

${dL \over dx}={\partial L \over \partial u}u'+{\partial L \over \partial u'}u''+{\partial L \over \partial x}\,,$

where $u''={\frac {du'}{dx}}={\frac {d^{2}u}{dx^{2}}}$.

Rearranging this yields

$u'{\partial L \over \partial u}={dL \over dx}-{\partial L \over \partial u'}u''-{\partial L \over \partial x}\,.$

Thus, substituting this expression for $u'{\frac {\partial L}{\partial u}}$into the second equation of this derivation,

${dL \over dx}-{\partial L \over \partial u'}u''-{\partial L \over \partial x}-u'{\frac {d}{dx}}{\frac {\partial L}{\partial u'}}=0\,.$

By the product rule, the last term is re-expressed as

$u'{\frac {d}{dx}}{\frac {\partial L}{\partial u'}}={\frac {d}{dx}}\left({\frac {\partial L}{\partial u'}}u'\right)-{\frac {\partial L}{\partial u'}}u''\,,$

and rearranging,

${d \over dx}\left({L-u'{\frac {\partial L}{\partial u'}}}\right)={\partial L \over \partial x}\,.$

For the case of ${\frac {\partial L}{\partial x}}=0$, this reduces to

${d \over dx}\left({L-u'{\frac {\partial L}{\partial u'}}}\right)=0\,,$

so that taking the antiderivative results in the Beltrami identity,

$L-u'{\frac {\partial L}{\partial u'}}=C\,,$

where C is a constant.

Applications

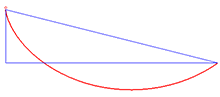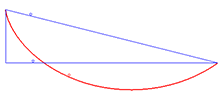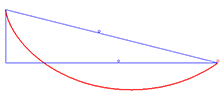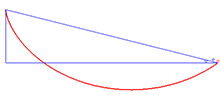
Solution to the brachistochrone problem

The solution to the brachistochrone problem is the cycloid.

An example of an application of the Beltrami identity is the brachistochrone problem, which involves finding the curve $y=y(x)$ that minimizes the integral

$I[y]=\int _{0}^{a}{\sqrt {{1+y'^{\,2}} \over y}}dx\,.$

The integrand

$L(y,y')={\sqrt {{1+y'^{\,2}} \over y}}$

does not depend explicitly on the variable of integration $x$, so the Beltrami identity applies,

$L-y'{\frac {\partial L}{\partial y'}}=C\,.$

Substituting for $L$ and simplifying,

$y(1+y'^{\,2})=1/C^{2}~~{\text{(constant)}}\,,$

which can be solved with the result put in the form of parametric equations

$x=A(\phi -\sin \phi )$

$y=A(1-\cos \phi )$

with $A$ being half the above constant, ${\frac {1}{2C^{2}}}$, and $\phi$ being a variable. These are the parametric equations for a cycloid.