Ancient Mesopotamian units of measurement

Ancient Mesopotamian units of measurement originated in the loosely organized city-states of Early Dynastic Sumer. Each city, kingdom and trade guild had its own standards until the formation of the Akkadian Empire when Sargon of Akkad issued a common standard. This standard was improved by Naram-Sin, but fell into disuse after the Akkadian Empire dissolved. The standard of Naram-Sin was readopted in the Ur III period by the Nanše Hymn which reduced a plethora of multiple standards to a few agreed upon common groupings. Successors to Sumerian civilization including the Babylonians, Assyrians, and Persians continued to use these groupings. Akkado-Sumerian metrology has been reconstructed by applying statistical methods to compare Sumerian architecture, architectural plans, and issued official standards such as Statue B of Gudea and the bronze cubit of Nippur.
Archaic system

The systems that would later become the classical standard for Mesopotamia were developed in parallel with writing during Uruk Period Sumer (c 4000 BCE). Studies of protocuneiform indicate twelve separate counting systems used in Uruk.
- Sexagesimal System S used to count slaves, animals, fish, wooden objects, stone objects, containers.
- Sexagesimal System S' used to count dead animals, certain types of beer
- Bi-Sexagesimal System B used to count cereal, bread, fish, milk products
- Bi-Sexagesimal System B* used to count rations
- GAN2 System G used to count field measurement
- ŠE system Š used to count barley by volume
- ŠE system Š' used to count malt by volume
- ŠE system Š" used to count wheat by volume
- ŠE System Š* used to count barley groats
- EN System E used to count weight
- U4 System U used to count calendrics
- DUGb System Db used to count milk by volume
- DUGc System Db used to count beer by volume
In Early Dynastic Sumer (c 2900–2300 BCE) metrology and mathematics were indistinguishable and treated as a single scribal discipline. The idea of an abstract number did not yet exist, thus all quantities were written as metrological symbols and never as numerals followed by a unit symbol. For example there was a symbol for one-sheep and another for one-day but no symbol for one. About 600 of these metrological symbols exist, for this reason archaic Sumerian metrology is complex and not fully understood.[1] In general however, length, volume, and mass are derived from a theoretical standard cube, called 'gur', filled with barley, wheat, water, or oil. However, because of the different specific gravities of these substances combined with dual numerical bases (sexagesimal or decimal), multiple sizes of the gur-cube were used without consensus. The different gur-cubes are related by proportion, based on the water gur-cube, according to four basic coefficients and their cubic roots.[citation needed] These coefficients are given as:
- Komma = 80⁄81 correction when planning rations with a 360-day year
- Leimma = 24⁄25 conversion from decimal to a sexagesimal number system
- Diesis = 15⁄16
- Euboic = 5⁄6
One official government standard of measurement of the archaic system was the Cubit of Nippur (2650 BCE). It is a Euboic Mana + 1 Diesis (432 grams).[citation needed] This standard is the main reference used by archaeologists to reconstruct the system.
Classical system
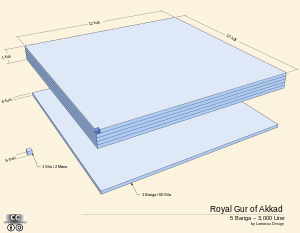
A major improvement came in 2150 BCE during the Akkadian Empire under the reign of Naram-Sin when the competing systems were unified by a single official standard, the royal gur-cube.[2] His reform is considered the first standardized system of measure in Mesopotamia.[2] The royal gur-cube (Cuneiform: LU2.GAL.GUR, 𒈚𒄥; Akkadian: šarru kurru) was a theoretical cuboid of water approximately 6 m × 6 m × 0.5 m from which all other units could be derived. The Neo-Sumerians continued use of the royal gur-cube as indicated by the Letter of Nanse issued in 2000 BCE by Gudea. Use of the same standard continued through the Babylonian, Assyrian, and Persian Empires.[1]
Length
Units of length are prefixed by the logogram DU (𒁺) a convention of the archaic period counting system from which it was evolved. Basic length was used in architecture and field division.
| Basic Length | ||||||
|---|---|---|---|---|---|---|
| Unit | Ratio | Sumerian | Akkadian | Cuneiform | ||
| grain | 1⁄180 | še | uţţatu | 𒊺 | ||
| finger | 1⁄30 | šu-si | ubānu | 𒋗𒋛 | ||
| foot | 2⁄3 | šu-du3-a | šīzu | 𒋗𒆕𒀀 | ||
| cubit | 1 | kuš3 | ammatu | 𒌑 | ||
| step | 2 | ĝiri3 | šēpu | 𒈨𒊑 | ||
| reed | 6 | gi | qanû | 𒄀 | ||
| rod | 12 | nindan | nindanu | 𒃻 | ||
| cord | 120 | eše2 | aslu | 𒂠 | ||
Distance units were geodectic as distinguished from non-geodectic basic length units. Sumerian geodesy divided latitude into seven zones between equator and pole.
| Distance | ||||||
|---|---|---|---|---|---|---|
| Unit | Ratio | Sumerian | Akkadian | Cuneiform | ||
| rod | 1⁄60 | nidan | nindanu | 𒃻 | ||
| cord | 1⁄6 | eše2 | aslu | 𒂠 | ||
| cable | 1 | uš | uš | 𒍑 | ||
| league | 30 | da-na | bêru | 𒁕𒈾 | ||
Area
The GAN2 system G counting system evolved into area measurements. A special unit measuring brick quantity by area was called the brick-garden (Cuneiform: SIG.SAR 𒊬𒋞; Sumerian: šeg12-sar; Akkadian: libittu-mūšaru) which held 720 bricks.
| Basic Area | ||||||
|---|---|---|---|---|---|---|
| Unit | Ratio | Dimensions | Sumerian | Akkadian | Cuneiform | |
| shekel | 1⁄60 | 1 kuš3 × 1 kuš3 | gin2 | šiqlu | 𒂆 | |
| garden | 1 | 12 kuš3 × 12 kuš3 | sar | mūšaru | 𒊬 | |
| quarter-field | 5 | 60 kuš3 × 60 kuš3 | uzalak | ? | 𒀺 | |
| half-field | 10 | 120 kuš3 × 60 kuš3 | upu | ubû | 𒀹𒃷 | |
| field | 100 | 60 ĝiri3 × 60 ĝiri3 | iku | ikû | 𒃷 | |
| estate | 1,800 | 3 eše2 × 6 eše2 | bur | būru | 𒁓 | |
Capacity or volume
Capacity was measured by either the ŠE system Š for dry capacity or the ŠE system Š* for wet capacity
| Basic Volume | ||||||
|---|---|---|---|---|---|---|
| Unit | Ratio | Sumerian | Akkadian | Cuneiform | ||
| shekel | 1⁄60 | gin2 | šiqlu | 𒂆 | ||
| bowl | 1 | sila3 | qû | 𒋡 | ||
| vessel | 10 | ban2 | sutū | 𒑏 | ||
| bushel | 60 | ba-ri2-ga | parsiktu | 𒁀𒌷𒂵 | ||
| gur-cube | 300 | gur | kurru | 𒄥 | ||
Mass or weight

Mass was measured by the EN system E
Values below are an average of weight artifacts from Ur and Nippur. The ± value represents 1 standard deviation. All values have been rounded to second digit of the standard deviation.
| Basic Mass | ||||||
|---|---|---|---|---|---|---|
| Unit | Ratio | Mean Value | Sumerian | Akkadian | Cuneiform | |
| grain | 1⁄180 | 46.6±1.9 mg | še | uţţatu | 𒊺 | |
| shekel | 1 | 8.40±0.34 g | gin2 | šiqlu | 𒂆 | |
| mina | 60 | 504±20 g | ma-na | manû | 𒈠𒈾 | |
| talent | 3,600 | 30.2±1.2 kg | gun2 | biltu or kakaru | 𒄘 | |
Time
In the Archaic System time notation was written in the U4 System U. Multiple lunisolar calendars existed; however the civil calendar from the holy city of Nippur (Ur III period) was adopted by Babylon as their civil calendar.[6] The calendar of Nippur dates to 3500 BCE and was itself based on older astronomical knowledge of an uncertain origin. The main astronomical cycles used to construct the calendar were the synodic month, equinox year, and sidereal day.
| Basic Time | ||||||
|---|---|---|---|---|---|---|
| Unit | Ratio | Sumerian | Akkadian | Cuneiform | ||
| gesh | 1⁄360 | mu-eš | geš | 𒈬𒍑 | ||
| watch | 1⁄12 | da-na | bêru | 𒂆 | ||
| day | 1 | ud | immu | 𒌓 | ||
| month | 30 | itud | arhu | 𒌗 | ||
| year | 360 | mu | šattu | 𒈬 | ||
Relationship to other metrologies
The Classical Mesopotamian system formed the basis for Elamite, Hebrew, Urartian, Hurrian, Hittite, Ugaritic, Phoenician, Babylonian, Assyrian, Persian, Arabic, and Islamic metrologies.[7] The Classical Mesopotamian System also has a proportional relationship, by virtue of standardized commerce, to Bronze Age Harappan and Egyptian metrologies.
See also
References
Citations
- ^ a b Melville 2006.
- ^ a b Powell 1995, p.1955.
- ^ https://www.academia.edu/2916303/Mesopotamian_Mensuration_Balance_Pan_Weights_from_Nippur
- ^ https://www.academia.edu/2916278/Weighing_in_Mesopotamia_The_Balance_Pan_Weights_from_Ur
- ^ Pentiuc, Eugen J. (14 August 2018). West Semitic Vocabulary in the Akkadian Texts from Emar. ISBN 9789004369870.
- ^ Ronan, 2008
- ^ Conder 1908, p. 87.
Bibliography
- Conder, Claude Reignier (1908). The Rise of Man. University of Michigan: J. Murray. pp. 368.
hittite metrology.
- Melville, Duncan J (2006-06-06). "Old Babylonian Weights and Measures". Archived from the original on 13 May 2008. Retrieved 2008-06-28.
- Powell, Marvin A (1995). "Metrology and Mathematics in Ancient Mesopotamia". In Sasson, Jack M. (ed.). Civilizations of the Ancient Near East. Vol. III. New York, NY: Charles Scribner’s Sons. pp. 3024. ISBN 0-684-19279-9.
- Ronan, Colin Alistair (2008). "Measurement of time and types of calendars » Standard units and cycles". Encyclopædia Britannica Online. Archived from the original on 25 June 2008. Retrieved 2008-06-28.
- Whitrow, G.J. (1988). Time in History: Views of Time from Prehistory to the Present Day. New York: Oxford University Press. pp. 217. ISBN 0-19-285211-6.
Further reading
- Katz, Victor,J (2007). The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook. Princeton University Press. p. 712. ISBN 978-0-691-11485-9.
{{cite book}}: CS1 maint: multiple names: authors list (link) - Nissen, Hans Jörg; Peter Damerow; Robert K. Englund; Paul Larsen (1993). Archaic Bookkeeping: Early Writing and Techniques of Economic Administration. University of Chicago Press. p. 169. ISBN 0-226-58659-6.
- Robson, Eleanor (1999). Mesopotamian Mathematics, 2100–1600 BC: Technical Constants in Bureaucracy. Oxford University Press. ISBN 0-19-815246-9.
- Sarton, George (1993). Ancient science through the golden age of Greece. Courier Dover Publications. p. 646. ISBN 0-486-27495-0.
External links
- An online calculator [1]
- Robson, Eleanor (2007). "Digital Corpus of Cuneiform Mathematical Texts". Archived from the original on 2009-01-16. Retrieved 2008-08-13.
- Aleff, H. Peter (2008). "Auspicious latitudes". Retrieved 2008-08-13.
- Kreidik, L. G.; T. S. Kortneva; G. P. Shpenkov (2005). "4. Fundamental periods of the World and ancient metrology". Journal of Theoretical Dialectics-Physics-Mathematics. Dialectical Academy, Russia-Belarus. Retrieved 2009-08-20.
