Busy beaver
This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these messages)
|

In theoretical computer science, the busy beaver game aims at finding a terminating program of a given size that (depending on definition) either produces the most output possible, or runs for the longest number of steps.[2] Since an endlessly looping program producing infinite output or running for infinite time is easily conceived, such programs are excluded from the game.[2] Rather than traditional programming languages, the programs used in the game are n-state Turing machines,[2] one of the first mathematical models of computation.[3]
Turing machines consist of an infinite tape, and a finite set of states which serve as the program's "source code". Producing the most output is defined as writing the largest number of 1s on the tape, also referred to as achieving the highest score, and running for the longest time is defined as taking the longest number of steps to halt.[4] The n-state busy beaver game consists of finding the longest-running or highest-scoring Turing machine which has n states and eventually halts.[2] Such machines are assumed to start on a blank tape, and the tape is assumed to contain only zeros and ones (a binary Turing machine).[2] The objective of the game is to program a set of transitions between states aiming for the highest score or longest running time while making sure the machine will halt eventually.
An nth busy beaver, BB-n or simply "busy beaver" is a Turing machine that wins the n-state busy beaver game.[5] Depending on definition, it either attains the highest score, or runs for the longest time, among all other possible n-state competing Turing machines. The functions determining the highest score or longest running time of the n-state busy beavers by each definition are Σ(n) and S(n) respectively.[4]
Deciding the running time or score of the nth Busy Beaver is incomputable.[4] In fact, both the functions Σ(n) and S(n) eventually become larger than any computable function.[4] This has implications in computability theory, the halting problem, and complexity theory.[6] The concept was first introduced by Tibor Radó in his 1962 paper, "On Non-Computable Functions".[4] One of the most interesting aspects of the busy beaver game is that, if it were possible to compute the functions Σ(n) and S(n) for all n, then this would resolve all mathematical conjectures which can be encoded as "does this Turing machine halt or not".[5] For example, a 27-state Turing machine could check Goldbach's conjecture for each number and halt on a counterexample: if this machine had not halted after running for S(27) steps, then it must run forever, resolving the conjecture.[5] Many other problems, including the Riemann hypothesis (744 states) and the consistency of ZF set theory (745 states[7][8]), can be expressed in a similar form, where at most a countably infinite number of cases need to be checked.[5]
Technical definition
[edit]
The n-state busy beaver game (or BB-n game), introduced in Tibor Radó's 1962 paper, involves a class of Turing machines, each member of which is required to meet the following design specifications:
- The machine has n "operational" states plus a Halt state, where n is a positive integer, and one of the n states is distinguished as the starting state. (Typically, the states are labelled by 1, 2, ..., n, with state 1 as the starting state, or by A, B, C, ..., with state A as the starting state.)
- The machine uses a single two-way infinite (or unbounded) tape.
- The tape alphabet is {0, 1}, with 0 serving as the blank symbol.
- The machine's transition function takes two inputs:
- the current non-Halt state,
- the symbol in the current tape cell,
- and produces three outputs:
- a symbol to write over the symbol in the current tape cell (it may be the same symbol as the symbol overwritten),
- a direction to move (left or right; that is, shift to the tape cell one place to the left or right of the current cell), and
- a state to transition into (which may be the Halt state).
"Running" the machine consists of starting in the starting state, with the current tape cell being any cell of a blank (all-0) tape, and then iterating the transition function until the Halt state is entered (if ever). If, and only if, the machine eventually halts, then the number of 1s finally remaining on the tape is called the machine's score. The n-state busy beaver (BB-n) game is therefore a contest, depending on definition to find such an n-state Turing machine having the largest possible score or running time.
Example
[edit]The rules for one 1-state Turing machine might be:
- In state 1, if the current symbol is 0, write a 1, move one space to the right, and transition to state 1
- In state 1, if the current symbol is 1, write a 0, move one space to the right, and transition to HALT
This Turing machine would move to the right, swapping the value of all the bits it passes. Since the starting tape is all 0s, it would make an unending string of ones. This machine would not be a busy beaver contender because it runs forever on a blank tape.
Functions
[edit]In his original 1962 paper, Radó defined two functions related to the busy beaver game: the score function Σ(n) and the shifts function S(n).[4] Both take a number of Turing machine states and output the maximum score attainable by a Turing machine of that number of states by some measure. The score function Σ(n) gives the maximum number of 1s an -state Turing machine can output before halting, while the shifts function S(n) gives the maximum number of shifts (or equivalently steps, because each step includes a shift) that an -state Turing machine can undergo before halting.[4] He proved that both of these functions were noncomputable, because they each grew faster than any computable function.[4] The function BB(n) has been defined to be either of these functions,[citation needed] so that notation is not used in this article.
A number of other uncomputable functions can also be defined based on measuring the performance of Turing machines in other ways than time or maximal number of ones.[9] For example:[9]
- The function is defined to be the maximum number of contiguous ones a halting Turing machine can write on a blank tape. In other words, this is the largest unary number a Turing machine of n states can write on a tape.
- The function is defined to be the maximal number of tape squares a halting Turing machine can read (i.e., visit) before halting. This includes the starting square, but not a square that the machine only reaches after the halt transition (if the halt transition is annotated with a move direction), because that square does not influence the machine's behaviour. This is the maximal space complexity of an n-state Turing machine.
These four functions together stand in the relation .[9] More functions can also be defined by operating the game on different computing machines, such as 3-symbol Turing machines,[10] non-deterministic Turing machines,[11] the lambda calculus (sequence A333479 in the OEIS) or even arbitrary programming languages.[10]
Score function Σ
[edit]The score function quantifies the maximum score attainable by a busy beaver on a given measure. This is a noncomputable function, because it grows asymptotically faster than any computable function.[12]
The score function, , is defined so that Σ(n) is the maximum attainable score (the maximum number of 1s finally on the tape) among all halting 2-symbol n-state Turing machines of the above-described type, when started on a blank tape.
It is clear that Σ is a well-defined function: for every n, there are at most finitely many n-state Turing machines as above, up to isomorphism, hence at most finitely many possible running times.
According to the score-based definition, any n-state 2-symbol Turing machine M for which σ(M) = Σ(n) (i.e., which attains the maximum score) is called a busy beaver. For each n, there exist at least 4(n − 1)! n-state busy beavers. (Given any n-state busy beaver, another is obtained by merely changing the shift direction in a halting transition, a third by reversing all shift directions uniformly, and a fourth by reversing the halt direction of the all-swapped busy beaver. Furthermore, a permutation of all states except Start and Halt produces a machine that attains the same score. Theoretically, there could be more than one kind of transition leading to the halting state, but in practice it would be wasteful, because there is only one sequence of state transitions producing the sought-after result.)
Non-computability
[edit]Radó's 1962 paper proved that if is any computable function, then Σ(n) > f(n) for all sufficiently large n, and hence that Σ is not a computable function.[4]
Moreover, this implies that it is undecidable by a general algorithm whether an arbitrary Turing machine is a busy beaver. (Such an algorithm cannot exist, because its existence would allow Σ to be computed, which is a proven impossibility. In particular, such an algorithm could be used to construct another algorithm that would compute Σ as follows: for any given n, each of the finitely many n-state 2-symbol Turing machines would be tested until an n-state busy beaver is found; this busy beaver machine would then be simulated to determine its score, which is by definition Σ(n).)
Even though Σ(n) is an uncomputable function, there are some small n for which it is possible to obtain its values and prove that they are correct. It is not hard to show that Σ(0) = 0, Σ(1) = 1, Σ(2) = 4, and with progressively more difficulty it can be shown that Σ(3) = 6, Σ(4) = 13 and Σ(5) = 4098 (sequence A028444 in the OEIS). Σ(n) has not yet been determined for any instance of n > 5, although lower bounds have been established (see the Known values section below).
Complexity and unprovability of Σ
[edit]A variant of Kolmogorov complexity is defined as follows:[13] The complexity of a number n is the smallest number of states needed for a BB-class Turing machine that halts with a single block of n consecutive 1s on an initially blank tape. The corresponding variant of Chaitin's incompleteness theorem states that, in the context of a given axiomatic system for the natural numbers, there exists a number k such that no specific number can be proven to have complexity greater than k, and hence that no specific upper bound can be proven for Σ(k) (the latter is because "the complexity of n is greater than k" would be proven if n > Σ(k) were proven). As mentioned in the cited reference, for any axiomatic system of "ordinary mathematics" the least value k for which this is true is far less than 10⇈10; consequently, in the context of ordinary mathematics, neither the value nor any upper-bound of Σ(10⇈10) can be proven. (Gödel's first incompleteness theorem is illustrated by this result: in an axiomatic system of ordinary mathematics, there is a true-but-unprovable sentence of the form Σ(10⇈10) = n, and there are infinitely many true-but-unprovable sentences of the form Σ(10⇈10) < n.)
Maximum shifts function S
[edit]In addition to the function Σ, Radó [1962] introduced another extreme function for Turing machines, the maximum shifts function, S, defined as follows:[4]
- s(M) = the number of shifts M makes before halting, for any M ∈ En,
- S(n) = max{s(M) | M ∈ En} = the largest number of shifts made by any halting n-state 2-symbol Turing machine.
Because normal Turing machines are required to have a shift in each and every transition or "step" (including any transition to a Halt state), the max-shifts function is at the same time a max-steps function.
Radó showed that S is noncomputable for the same reason that Σ is noncomputable — it grows faster than any computable function. He proved this simply by noting that for each n, S(n) ≥ Σ(n). Each shift may write a 0 or a 1 on the tape, while Σ counts a subset of the shifts that wrote a 1, namely the ones that hadn't been overwritten by the time the Turing machine halted; consequently, S grows at least as fast as Σ, which had already been proved to grow faster than any computable function.[4]
The following connection between Σ and S was used by Lin & Radó [Computer Studies of Turing Machine Problems, 1965] to prove that Σ(3) = 6 and that S(6)=21: For a given n, if S(n) is known then all n-state Turing machines can (in principle) be run for up to S(n) steps, at which point any machine that hasn't yet halted will never halt. At that point, by observing which machines have halted with the most 1s on the tape (i.e., the busy beavers), one obtains from their tapes the value of Σ(n). The approach used by Lin & Radó for the case of n = 3 was to conjecture that S(3) = 21 (after unsuccessfully conjecturing 18), then to simulate all the essentially different 3-state machines (82,944 machines, equal to 21034) for up to 21 steps. They found 26,073 machines that halted, including one that halted only after 21 steps. By analyzing the behavior of the machines that had not halted within 21 steps, they succeeded in showing that none of those machines would ever halt, most of them following a certain pattern. This proved the conjecture that S(3) = 21, and also determined that Σ(3) = 6, which was attained by several machines, all halting after 11 to 14 steps.[14]
In 2016, Adam Yedidia and Scott Aaronson obtained the first (explicit) upper bound on the minimum n for which S(n) is unprovable in ZFC. To do so they constructed a 7910-state[15] Turing machine whose behavior cannot be proven based on the usual axioms of set theory (Zermelo–Fraenkel set theory with the axiom of choice), under reasonable consistency hypotheses (stationary Ramsey property).[16][17] Stefan O'Rear then reduced it to 1919 states, with the dependency on the stationary Ramsey property eliminated,[18][19] and later to 748 states.[6] In July 2023, Riebel reduced it to 745 states.[7][8]
Proof for uncomputability of S(n) and Σ(n)
[edit]Suppose that S(n) is a computable function and let EvalS denote a TM, evaluating S(n). Given a tape with n 1s it will produce S(n) 1s on the tape and then halt. Let Clean denote a Turing machine cleaning the sequence of 1s initially written on the tape. Let Double denote a Turing machine evaluating function n + n. Given a tape with n 1s it will produce 2n 1s on the tape and then halt. Let us create the composition Double | EvalS | Clean and let n0 be the number of states of this machine. Let Create_n0 denote a Turing machine creating n0 1s on an initially blank tape. This machine may be constructed in a trivial manner to have n0 states (the state i writes 1, moves the head right and switches to state i + 1, except the state n0, which halts). Let N denote the sum n0 + n0.
Let BadS denote the composition Create_n0 | Double | EvalS | Clean. Notice that this machine has N states. Starting with an initially blank tape it first creates a sequence of n0 1s and then doubles it, producing a sequence of N 1s. Then BadS will produce S(N) 1s on tape, and at last it will clear all 1s and then halt. But the phase of cleaning will continue at least S(N) steps, so the time of working of BadS is strictly greater than S(N), which contradicts to the definition of the function S(n).
The uncomputability of Σ(n) may be proved in a similar way. In the above proof, one must exchange the machine EvalS with EvalΣ and Clean with Increment — a simple TM, searching for a first 0 on the tape and replacing it with 1.
The uncomputability of S(n) can also be established by reference to the blank tape halting problem. The blank tape halting problem is the problem of deciding for any Turing machine whether or not it will halt when started on an empty tape. The blank tape halting problem is equivalent to the standard halting problem and so it is also uncomputable. If S(n) was computable, then we could solve the blank tape halting problem simply by running any given Turing machine with n states for S(n) steps; if it has still not halted, it never will. So, since the blank tape halting problem is not computable, it follows that S(n) must likewise be uncomputable.
Uncomputability of space(n) and num(n)
[edit]Both and functions are uncomputable .[9] This can be shown for by noting that every tape square a Turing machine writes a one to, it must also visit: in other words, .[9] The function can be shown to be incomputable by proving, for example, that : this can be done by designing an (3n+3)-state Turing machine which simulates the n-state space champion, and then uses it to write at least contiguous ones to the tape.[9]
Generalizations
[edit]Analogs of the shift function can be simply defined in any programming language, given that the programs can be described by bit-strings, and a program's number of steps can be counted.[10] For example, the busy beaver game can also be generalized to two dimensions using Turing machines on two-dimensional tapes, or to Turing machines that are allowed to stay in the same place as well as move to the left and right.[10] Alternatively a "busy beaver function" for diverse models of computation can be defined with Kolmogorov complexity.[10] This is done by taking to be the largest integer such that , where is the length of the shortest program in that outputs : is thereby the largest integer a program with length or less can output in .[10]
The longest running 6-state, 2-symbol machine which has the additional property of reversing the tape value at each step produces 6147 1s after 47339970 steps.[citation needed] So for the Reversal Turing Machine (RTM) class,[20] SRTM(6) ≥ 47339970 and ΣRTM(6) ≥ 6147. Likewise we could define an analog to the Σ function for register machines as the largest number which can be present in any register on halting, for a given number of instructions.[citation needed]
Different numbers of symbols
[edit]A simple generalization is the extension to Turing machines with m symbols instead of just 2 (0 and 1).[10] For example a trinary Turing machine with m = 3 symbols would have the symbols 0, 1, and 2. The generalization to Turing machines with n states and m symbols defines the following generalized busy beaver functions:
- Σ(n, m): the largest number of non-zeros printable by an n-state, m-symbol machine started on an initially blank tape before halting,[citation needed] and
- S(n, m): the largest number of steps taken by an n-state, m-symbol machine started on an initially blank tape before halting.[10]
For example, the longest-running 3-state 3-symbol machine found so far runs 119112334170342540 steps before halting.[21][better source needed]
Nondeterministic Turing machines
[edit]| p | steps | states |
|---|---|---|
| 1 | 2 | 2 |
| 2 | 4 | 4 |
| 3 | 6 | 7 |
| 4 | 7 | 11 |
| 5 | 8 | 15 |
| 6 | 7 | 18 |
| 7 | 6 | 18 |
The problem can be extended to nondeterministic Turing machines by looking for the system with the most states across all branches or the branch with the longest number of steps.[11] The question of whether a given NDTM will halt is still computationally irreducible, and the computation required to find an NDTM busy beaver is significantly greater than the deterministic case, since there are multiple branches that need to be considered. For a 2-state, 2-color system with p cases or rules, the table to the right gives the maximum number of steps before halting and maximum number of unique states created by the NDTM.
Applications
[edit]Open mathematical problems
[edit]In addition to posing a rather challenging mathematical game, the busy beaver functions Σ(n) and S(n) offer an entirely new approach to solving pure mathematics problems. Many open problems in mathematics could in theory, but not in practice, be solved in a systematic way given the value of S(n) for a sufficiently large n.[5][22] Theoretically speaking, the value of S(n) encodes the answer to all mathematical conjectures that can be checked in infinite time by a Turing machine with less than or equal to n states.[6]
Consider any conjecture: any conjecture that could be disproven via a counterexample among a countable number of cases (e.g. Goldbach's conjecture). Write a computer program that sequentially tests this conjecture for increasing values. In the case of Goldbach's conjecture, we would consider every even number ≥ 4 sequentially and test whether or not it is the sum of two prime numbers. Suppose this program is simulated on an n-state Turing machine. If it finds a counterexample (an even number ≥ 4 that is not the sum of two primes in our example), it halts and indicates that. However, if the conjecture is true, then our program will never halt. (This program halts only if it finds a counterexample.)[6]
Now, this program is simulated by an n-state Turing machine, so if we know S(n) we can decide (in a finite amount of time) whether or not it will ever halt by simply running the machine that many steps. And if, after S(n) steps, the machine does not halt, we know that it never will and thus that there are no counterexamples to the given conjecture (i.e., no even numbers that are not the sum of two primes). This would prove the conjecture to be true.[6] Thus specific values (or upper bounds) for S(n) could be, in theory, used to systematically solve many open problems in mathematics.[6]
However, current results on the busy beaver problem suggest that this will not be practical for two reasons:[citation needed]
- It is extremely hard to prove values for the busy beaver function (and the max shift function). Every known exact value of S(n) was proven by enumerating every n-state Turing machine and proving whether or not each halts. One would have to calculate S(n) by some less direct method for it to actually be useful.[citation needed]
- The values of S(n) and the other busy beaver functions get very large, very quickly. While the value of S(5) is only around 47 million, the value of S(6) is more than 10⇈15, which is equal to with a stack of 15 tens.[10][better source needed] This number has 10⇈14 digits and is unreasonable to use in a computation. The value of S(27), which is the number of steps the current program for the Goldbach conjecture would need to be run to give a conclusive answer, is incomprehensibly huge, and not remotely possible to write down, much less run a machine for, in the observable universe.[5]
Consistency of theories
[edit]Another property of S(n) is that no arithmetically sound, computably axiomatized theory can prove all of the function's values. Specifically, given a computable and arithmetically sound theory , there is a number such that for all , no statement of the form can be proved in .[6] This implies that for each theory there is a specific largest value of S(n) that it can prove. This is true because for every such , a Turing machine with states can be designed to enumerate every possible proof in .[6] If the theory is inconsistent, then all false statements are provable, and the Turing machine can be given the condition to halt if and only if it finds a proof of, for example, .[6] Any theory that proves the value of proves its own consistency, violating Gödel's second incompleteness theorem.[6] This can be used to place various theories on a scale, for example the various large cardinal axioms in ZFC: if each theory is assigned as its number , theories with larger values of prove the consistency of those below them, placing all such theories on a countably infinite scale.[6]
Notable examples
[edit]- A 745-state binary Turing machine has been constructed that halts if and only if ZFC is inconsistent.[7][8]
- A 744-state Turing machine has been constructed that halts if, and only if, the Riemann hypothesis is false.[18][5]
- In 2016, a 43-state Turing machine was constructed that halts if, and only if, Goldbach's conjecture is false. This was further reduced to 27-state machine, [18][5] and in 2024 this construction was formally proved and verified in the Lean 4 theorem proving language.[23]
- A 15-state Turing machine has been constructed that halts if and only if the following conjecture formulated by Paul Erdős in 1979 is false: for all n > 8 there is at least one digit 2 in the base 3 representation of 2n.[24][25]
Universal Turing machines
[edit]Exploring the relationship between computational universality and the dynamic behavior of Busy Beaver Turing machines, a conjecture was proposed in 2012[26] suggesting that Busy Beaver machines were natural candidates for Turing universality as they display complex characteristics, known for (1) their maximal computational complexity within size constraints, (2) their ability to perform non-trivial calculations before halting, and (3) the difficulty in finding and proving these machines; these features suggest that Busy Beaver machines possess the necessary complexity for universality.
Known results
[edit]Lower bounds
[edit]Green machines
[edit]In 1964 Milton Green developed a lower bound for the 1s-counting variant of the Busy Beaver function that was published in the proceedings of the 1964 IEEE symposium on switching circuit theory and logical design. Heiner Marxen and Jürgen Buntrock described it as "a non-trivial (not primitive recursive) lower bound".[27] This lower bound can be calculated but is too complex to state as a single expression in terms of n.[28] This was done with a set of Turing machines, each of which demonstrated the lower bound for a certain n.[28] When n=8 the method gives
- .
In contrast, the best current (as of 2024) lower bound on is , where each is Knuth's up-arrow notation.[10] This represents , an exponentiated chain of 15 tens equal to . The value of is probably much larger still than that.
Specifically, the lower bound was shown with a series of recursive Turing machines, each of which was made of a smaller one with two additional states that repeatedly applied the smaller machine to the input tape.[28] Defining the value of the N-state busy-beaver competitor on a tape containing ones to be (the ultimate output of each machine being its value on , because a blank tape has 0 ones), the recursion relations are as follows:[28] a
This leads to two formulas, for odd and even numbers, for calculating the lower bound given by the Nth machine, :
- for odd N
- for even N
The lower bound BB(N) can also be related to the Ackermann function. It can be shown that:[29]
Relationships between Busy beaver functions
[edit]Trivially, S(n) ≥ Σ(n) because a machine that writes Σ(n) ones must take at least Σ(n) steps to do so.[29] It is possible to give a number of upper bounds on the time S(n) with the number of ones Σ(n):
By defining num(n) to be the maximum number of ones an n-state Turing machine is allowed to output contiguously, rather than in any position (the largest unary number it can output), it is possible to show:[29]
- (Ben-Amram, et al., 1996[9])
Ben-Amram and Petersen, 2002, also give an asymptotically improved bound on S(n). There exists a constant c, such that for all n ≥ 2:[29]
Exact values and lower and upper bounds
[edit]The following table lists the exact values and some known lower bounds for S(n), Σ(n), and several other busy beaver functions. In this table, 2-symbol Turing machines are used. Entries listed as "?" are at least as large as other entries to the left (because all n-state machines are also (n+1) state machines), and no larger than entries above them (because S(n) ≥ space(n) ≥ Σ(n) ≥ num(n)). So, space(6) is known to be greater than 10⇈15, as space(n) ≥ Σ(n) and Σ(6) > 10⇈15. 47176870 is an upper bound for space(5), because S(5) = 47176870 ([3]) and S(n) ≥ space(n). 4098 is an upper bound for num(5), because Σ(5) = 4098 ([29]) and Σ(n) ≥ num(n). The last entry listed as "?" is num(6), because Σ(6) > 10⇈15, but Σ(n) ≥ num(n).
| Function | 2-state | 3-state | 4-state | 5-state | 6-state |
|---|---|---|---|---|---|
| S(n) | 6 ([6]) | 21 ([6]) | 107 ([6]) | 47176870 ([3]) | > 10⇈15 ([10]) |
| space(n) | 4 ([29]) | 7 ([29]) | 16 ([29]) | ≥ 12289 ([29])
≤ 47176870 (S(n) ≥ space(n)) |
> 10⇈15 (space(n) ≥ Σ(n)) |
| Σ(n) | 4 ([29]) | 6 ([29]) | 13 ([29]) | 4098 ([29]) | > 10⇈15 ([30]) |
| num(n) | 4 ([29]) | 6 ([29]) | 12 ([29]) | ≤ 4098 (Σ(n) ≥ num(n)) | ? |
The 5-state busy beaver was discovered by Heiner Marxen and Jürgen Buntrock in 1989, but only proved to be the winning fifth busy beaver — stylized as BB(5) — in 2024 using a proof in Coq.[31][32]
List of busy beavers
[edit]
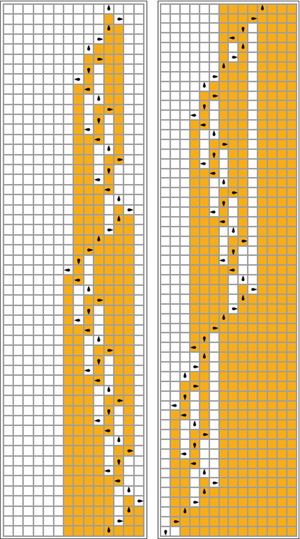
The diagram is compressed so only steps which change the tape are shown. Green and yellow triangles indicate regions where the Turing machine shuttles back and forth; the time taken is proportional to the areas of these colored triangles. The bottom row is an excerpt of the tape and the read/write head upon halting.
These are tables of rules for Turing machines that generate Σ(1) and S(1), Σ(2) and S(2), Σ(3) (but not S(3)), Σ(4) and S(4), Σ(5) and S(5), and the best known lower bound for Σ(6) and S(6).
In the tables, columns represent the current state and rows represent the current symbol read from the tape. Each table entry is a string of three characters, indicating the symbol to write onto the tape, the direction to move, and the new state (in that order). The halt state is shown as H.
Each machine begins in state A with an infinite tape that contains all 0s. Thus, the initial symbol read from the tape is a 0.
Result key: (starts at the position overlined, halts at the position underlined)
1-state, 2-symbol busy beaver A 0 1RH 1 (not used)
Result: 0 0 1 0 0 (1 step, one "1" total)
2-state, 2-symbol busy beaver[citation needed] A B 0 1RB 1LA 1 1LB 1RH
Result: 0 0 1 1 1 1 0 0 (6 steps, four "1"s total)

Result: 0 0 1 1 1 1 1 1 0 0 (14 steps, six "1"s total).
This is one of several nonequivalent machines giving six 1s. Unlike the previous machines, this one is a busy beaver for Σ, but not for S. (S(3) = 21, and the machine obtains only five 1s.[14])

4-state, 2-symbol busy beaver A B C D 0 1RB 1LA 1RH 1RD 1 1LB 0LC 1LD 0RA
Result: 0 0 1 0 1 1 1 1 1 1 1 1 1 1 1 1 0 0 (107 steps, thirteen "1"s total)
5-state, 2-symbol busy beaver A B C D E 0 1RB 1RC 1RD 1LA 1RH 1 1LC 1RB 0LE 1LD 0LA
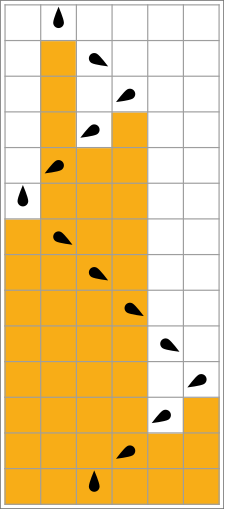
Result: 4098 "1"s with 8191 "0"s interspersed in 47,176,870 steps.
Note in the image to the right how this solution is similar qualitatively to the evolution of some cellular automata.
current 6-state, 2-symbol best contender[21][30] A B C D E F 0 1RB 1RC 1LC 0LE 1LF 0RC 1 0LD 0RF 1LA 1RH 0RB 0RE
Result: 1 0 1 1 1 ... 1 1 1 ("10" followed by more than 10↑↑15 contiguous "1"s in more than 10↑↑15 steps, where 10↑↑15=1010..10, an exponential tower of 15 tens).
Visualizations
[edit]In the following table, the rules for each busy beaver (maximizing Σ) are represented visually, with orange squares corresponding to a "1" on the tape, and white corresponding to "0". The position of the head is indicated by the black ovoid, with the orientation of the head representing the state. Individual tapes are laid out horizontally, with time progressing from top to bottom. The halt state is represented by a rule which maps one state to itself (head doesn't move).
See also
[edit]Notes
[edit]- ^ "The Busy Beaver Challenge: Story # space-time-diagrams". bbchallenge.org. Retrieved 2024-07-09.
- ^ a b c d e Weisstein, Eric W. "Busy Beaver". Wolfram MathWorld. Retrieved 21 November 2023.
- ^ a b c Brubaker, Ben (2024-07-02). "Amateur Mathematicians Find Fifth 'Busy Beaver' Turing Machine". Quanta Magazine. Retrieved 2024-07-03.
- ^ a b c d e f g h i j k Radó, Tibor (May 1962). "On non-computable functions" (PDF). Bell System Technical Journal. 41 (3): 877–884. doi:10.1002/j.1538-7305.1962.tb00480.x.
- ^ a b c d e f g h Pavlus, John (10 December 2020). "How the Slowest Computer Programs Illuminate Math's Fundamental Limits". Quanta Magazine. Retrieved 2020-12-11.
- ^ a b c d e f g h i j k l m n Aaronson, Scott (2020-09-29). "The Busy Beaver Frontier". SIGACT News. 51 (3): 32–54. doi:10.1145/3427361.3427369. ISSN 0163-5700. PDF available from author.
- ^ a b c "Life, blogging, and the Busy Beaver function go on". 2023-07-05. Retrieved 2023-08-27.
- ^ a b c Riebel, Johannes (March 2023). The Undecidability of BB(748): Understanding Gödel's Incompleteness Theorems (PDF) (Bachelor's thesis). University of Augsburg. Retrieved 24 September 2024.
- ^ a b c d e f g Ben-Amram, A. M.; Julstrom, B. A.; Zwick, U. (1996-08-01). "A note on busy beavers and other creatures". Mathematical Systems Theory. 29 (4): 375–386. doi:10.1007/BF01192693. ISSN 1433-0490.
- ^ a b c d e f g h i j k Aaronson, Scott (2024-07-02). "BusyBeaver(5) is now known to be 47,176,870". Shtetl-Optimized. Retrieved 2024-07-04.
- ^ a b c Wolfram, Stephen (4 February 2021). "Multiway Turing Machines". www.wolframphysics.org.
- ^ Chaitin (1987)
- ^ Boolos, Burgess & Jeffrey, 2007. "Computability and Logic"
- ^ a b c Lin, Shen; Rado, Tibor (April 1965). "Computer studies of Turing machine problems". Journal of the ACM. 12 (2): 196–212. doi:10.1145/321264.321270. S2CID 17789208.
- ^ Adam Yedidia and Scott Aaronson (May 2016). A Relatively Small Turing Machine Whose Behavior Is Independent of Set Theory (Technical Report). MIT. arXiv:1605.04343. Bibcode:2016arXiv160504343Y.
- ^ Aron, Jacob. "This Turing machine should run forever unless maths is wrong". NewScientist. Retrieved 2016-09-25.
- ^ Version from May 3rd contained 7918 states: "The 8000th Busy Beaver number eludes ZF set theory". Shtetl-Optimized blog. 2016-05-03. Retrieved 2016-09-25.
- ^ a b c "Three announcements". Shtetl-Optimized blog. 2016-05-03. Retrieved 2018-04-27.
- ^ "GitHub - sorear/metamath-turing-machines: Metamath proof enumerators and other things". GitHub. 2019-02-13.
- ^ "Reversal Turing machine". skelet.ludost.net. Retrieved 2022-02-10.
- ^ a b Pascal Michel's Busy Beaver Competitions page listing best contenders known.
- ^ Chaitin, Gregory J. (1987). "Computing the Busy Beaver Function" (PDF). In Cover, T. M.; Gopinath, B. (eds.). Open Problems in Communication and Computation. Springer. pp. 108–112. ISBN 978-0-387-96621-2. Archived from the original (PDF) on 2017-12-30. Retrieved 2022-07-07.
- ^ Leng, Yijun. "GitHub Repository "goldbach_tm27"". GitHub.
- ^ Tristan Stérin and Damien Woods (July 2021). On the hardness of knowing busy beaver values BB(15) and BB(5,4) (Technical Report). Maynooth University. arXiv:2107.12475.
- ^ Erdõs, Paul (1979). "Some unconventional problems in number theory". Math. Mag. 52 (2): 67–70. doi:10.1080/0025570X.1979.11976756. JSTOR 2689842.
- ^ Zenil, Hector (2012). "On the Dynamic Qualitative Behaviour of Universal Computation". Complex Systems. 20 (3): 265–277. doi:10.25088/ComplexSystems.20.3.265. ISSN 0891-2513. PDF available from publisher.
- ^ Brady, Allen H. (March 1998). "Heiner Marxen and Jürgen Buntrock. Attacking the busy beaver 5. Bulletin of the European Association for Theoretical Computer Science, no. 40 (Feb.1990), pp. 247–251. - Pascal Michel. Busy beaver competition and Collatz-like problems. Archive for mathematical logic, vol. 32 (1993), pp. 351–367". The Journal of Symbolic Logic. 63 (1): 331–332. doi:10.2307/2586607. ISSN 0022-4812. JSTOR 2586607. Free HTML version by author
- ^ a b c d Green, Milton W. (1964-11-11). "A lower bound RADO's sigma function for binary turing machines". Proceedings of the 1964 Proceedings of the Fifth Annual Symposium on Switching Circuit Theory and Logical Design. SWCT '64. USA: IEEE Computer Society: 91–94. doi:10.1109/SWCT.1964.3.
- ^ a b c d e f g h i j k l m n o p q r s Ben-Amram, A. M.; Petersen, H. (2002). "Improved bounds for functions related to busy beavers". Theory of Computing Systems. 35 (1): 1–11. doi:10.1007/s00224-001-1052-0. MR 1879169.
- ^ a b Ligocki, Shawn (2022-06-21). "BB(6, 2) > 10↑↑15". sligocki. Retrieved 2024-07-04.
- ^ "[July 2nd 2024] We have proved "BB(5) = 47,176,870"". The Busy Beaver Challenge. 2024-07-02. Retrieved 2024-07-02.
- ^ "The Busy Beaver Challenge". bbchallenge.org. Retrieved 2024-07-02.
- ^ Shen Lin (1963). Computer studies of Turing machine problems (Ph.D. thesis). Ohio State University.
References
[edit]- Radó, Tibor (May 1962). "On non-computable functions" (PDF). Bell System Technical Journal. 41 (3): 877–884. doi:10.1002/j.1538-7305.1962.tb00480.x.
- This is where Radó first defined the busy beaver problem and proved that it was uncomputable and grew faster than any computable function.
- Lin, Shen; Radó, Tibor (April 1965). "Computer Studies of Turing Machine Problems". Journal of the ACM. 12 (2): 196–212. doi:10.1145/321264.321270. S2CID 17789208.
- The results of this paper had already appeared in part in Lin's 1963 doctoral dissertation, under Radó's guidance. Lin & Radó prove that Σ(3) = 6 and S(3) = 21 by proving that all 3-state 2-symbol Turing Machines which don't halt within 21 steps will never halt. (Most are proven automatically by a computer program, however 40 are proven by human inspection.)
- Brady, Allen H. (April 1983). "The determination of the value of Rado's noncomputable function Σ(k) for four-state Turing machines". Mathematics of Computation. 40 (162): 647–665. doi:10.1090/S0025-5718-1983-0689479-6. JSTOR 2007539.
- Brady proves that Σ(4) = 13 and S(4) = 107. Brady defines two new categories for non-halting 3-state 2-symbol Turing Machines: Christmas Trees and Counters. He uses a computer program to prove that all but 27 machines which run over 107 steps are variants of Christmas Trees and Counters which can be proven to run infinitely. The last 27 machines (referred to as holdouts) are proven by personal inspection by Brady himself not to halt.
- Machlin, Rona; Stout, Quentin F. (June 1990). "The complex behavior of simple machines". Physica D: Nonlinear Phenomena. 42 (1–3): 85–98. Bibcode:1990PhyD...42...85M. doi:10.1016/0167-2789(90)90068-Z. hdl:2027.42/28528.
- Machlin and Stout describe the busy beaver problem and many techniques used for finding busy beavers (which they apply to Turing Machines with 4-states and 2-symbols, thus verifying Brady's proof). They suggest how to estimate a variant of Chaitin's halting probability (Ω).
- Marxen, Heiner; Buntrock, Jürgen (February 1990). "Attacking the Busy Beaver 5". Bulletin of the EATCS. 40: 247–251. Archived from the original on 2006-10-09. Retrieved 2020-01-19.
- Marxen and Buntrock demonstrate that Σ(5) ≥ 4098 and S(5) ≥ 47176870 and describe in detail the method they used to find these machines and prove many others will never halt.
- Green, Milton W. (1964). A Lower Bound on Rado's Sigma Function for Binary Turing Machines. 1964 Proceedings of the Fifth Annual Symposium on Switching Circuit Theory and Logical Design. pp. 91–94. doi:10.1109/SWCT.1964.3.
- Green recursively constructs machines for any number of states and provides the recursive function that computes their score (computes σ), thus providing a lower bound for Σ. This function's growth is comparable to that of Ackermann's function.
- Dewdney, Alexander K. (1984). "A computer trap for the busy beaver, the hardest working Turing machine". Scientific American. 251 (2): 10–17.
- Busy beaver programs are described by Alexander Dewdney in Scientific American, August 1984, pages 19–23, also March 1985 p. 23 and April 1985 p. 30.
- Chaitin, Gregory J. (1987). "Computing the Busy Beaver Function" (PDF). In Cover, T. M.; Gopinath, B. (eds.). Open Problems in Communication and Computation. Springer. pp. 108–112. ISBN 978-0-387-96621-2. Archived from the original (PDF) on 2017-12-30. Retrieved 2022-07-07.
- Brady, Allen H. (1995). "The Busy Beaver Game and the Meaning of Life". In Herken, Rolf (ed.). The Universal Turing Machine: A Half-Century Survey (2nd ed.). Wien, New York: Springer-Verlag. pp. 237–254. ISBN 978-3-211-82637-9.
- Wherein Brady (of 4-state fame) describes some history of the beast and calls its pursuit "The Busy Beaver Game". He describes other games (e.g. cellular automata and Conway's Game of Life). Of particular interest is "The Busy Beaver Game in Two Dimensions" (p. 247). With 19 references.
- Booth, Taylor L. (1967). Sequential Machines and Automata Theory. New York: Wiley. ISBN 978-0-471-08848-6.
- Cf Chapter 9, Turing Machines. A difficult book, meant for electrical engineers and technical specialists. Discusses recursion, partial-recursion with reference to Turing Machines, halting problem. A reference in Booth attributes busy beaver to Rado. Booth also defines Rado's busy beaver problem in "home problems" 3, 4, 5, 6 of Chapter 9, p. 396. Problem 3 is to "show that the busy beaver problem is unsolvable... for all values of n."
- Ben-Amram, A. M.; Julstrom, B. A.; Zwick, U. (1996). "A note on Busy Beavers and other creatures". Mathematical Systems Theory. 29 (4): 375–386. CiteSeerX 10.1.1.75.1297. doi:10.1007/BF01192693. S2CID 30937913. Archived from the original on 2018-07-21. Retrieved 2022-07-07.
- Bounds between functions Σ and S.
- Ben-Amram, A. M.; Petersen, H. (2002). "Improved Bounds for Functions Related to Busy Beavers". Theory of Computing Systems. 35: 1–11. CiteSeerX 10.1.1.136.5997. doi:10.1007/s00224-001-1052-0. S2CID 10429773.
- Improved bounds.
- Lafitte, G.; Papazian, C. (June 2007). "The fabric of small Turing machines". Computation and Logic in the Real World, Proceedings of the Third Conference on Computability in Europe. pp. 219–227. CiteSeerX 10.1.1.104.3021.
- This article contains a complete classification of the 2-state, 3-symbol Turing machines, and thus a proof for the (2, 3) busy beaver: Σ(2, 3) = 9 and S(2, 3) = 38.
- Boolos, George S.; Burgess, John P.; Jeffrey, Richard C. (2007). Computability and Logic (Fifth ed.). Cambridge University Press. ISBN 978-0-521-87752-7.
- Kropitz, Pavel (2010). Problém Busy Beaver (Bachelor thesis) (in Slovak). Charles University in Prague.
- This is the description of ideas, of the algorithms and their implementation, with the description of the experiments examining 5-state and 6-state Turing machines by parallel run on 31 4-core computer and finally the best results for 6-state TM.
External links
[edit]- The page of Heiner Marxen, who, with Jürgen Buntrock, found the above-mentioned records for a 5 and 6-state Turing machine.
- Pascal Michel's Historical survey of busy beaver results which also contains best results and some analysis.
- Definition of the class RTM - Reversal Turing Machines, simple and strong subclass of the TMs.
- "The Busy Beaver Problem: A New Millennium Attack" (archived) at the Rensselaer RAIR Lab. This effort found several new records and established several values for the quadruple formalization.
- Daniel Briggs' website archive and forum for solving the 5-state, 2-symbol busy beaver problem, based on Skelet (Georgi Georgiev) nonregular machines list.
- Ligocki, Shawn (2021-07-17). "Collatz-like behavior of Busy Beavers". sligocki. Retrieved 2022-07-12.
- Aaronson, Scott (1999), Who can name the bigger number?
- Weisstein, Eric W. "Busy Beaver". MathWorld.
- Busy Beaver Turing Machines - Computerphile, Youtube
- Pascal Michel. The Busy Beaver Competition: a historical survey. 70 pages. 2017. <hal-00396880v5>