Cantic 8-cube
Appearance
| Cantic 8-cube | |
|---|---|
 D8 Coxeter plane projection | |
| Type | uniform 8-polytope |
| Schläfli symbol | t0,1{3,35,1} |
| Coxeter-Dynkin diagram | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | |
| Vertices | |
| Vertex figure | ( )v{ }x{3,3,3,3} |
| Coxeter groups | D8, [35,1,1] |
| Properties | convex |
In eight-dimensional geometry, a cantic 8-cube or truncated 8-demicube is a uniform 8-polytope, being a truncation of the 8-demicube.
Alternate names
- Truncated demiocteract
- Truncated hemiocteract (Jonathan Bowers)
Cartesian coordinates
The Cartesian coordinates for the vertices of a truncated 8-demicube centered at the origin and edge length 6√2 are coordinate permutations:
- (±1,±1,±3,±3,±3,±3,±3,±3)
with an odd number of plus signs.
Images
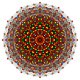
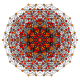
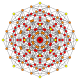
| Coxeter plane | B8 | D8 | D7 | D6 | D5 |
|---|---|---|---|---|---|
| Graph | 
|

|
|
|
|
| Dihedral symmetry | [16/2] | [14] | [12] | [10] | [8] |
| Coxeter plane | D4 | D3 | A7 | A5 | A3 |
| Graph | 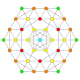
|
|
|
|
|
| Dihedral symmetry | [6] | [4] | [8] | [6] | [4] |
Notes
References
- H.S.M. Coxeter:
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D.
- Klitzing, Richard. "8D uniform polytopes (polyzetta) x3x3o *b3o3o3o3o3o".
External links
- Weisstein, Eric W. "Hypercube". MathWorld.
- Polytopes of Various Dimensions
- Multi-dimensional Glossary
