Jump to content

Discovery of the neutron

From Wikipedia, the free encyclopedia

This is an old revision of this page, as edited by ClueBot NG (talk | contribs) at 17:17, 27 November 2016 (Reverting possible vandalism by 2405:204:3089:6F5D:D119:8054:82F8:9D72 to version by SporkBot. Report False Positive? Thanks, ClueBot NG. (2850608) (Bot)). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.

James Chadwick discovered the neutron in 1932 while working at Cavendish Laboratory.

The story of the discovery of the neutron and its properties is central to the extraordinary developments in atomic physics that occurred in the first half of the 20th century. The century began with Ernest Rutherford and Thomas Royds proving, in 1908, that alpha radiation consists of helium ions.[1][2] and Rutherford's model for the atom in 1911,[3] in which atoms have their mass and positive charge concentrated in a very small nucleus.[4] The essential nature of the atomic nucleus was established with the discovery of the neutron by James Chadwick in 1932.

Rutherford atom

See also: Plum pudding model
A schematic of the nucleus of an atom indicating
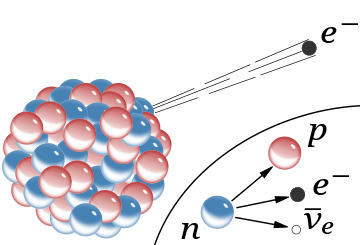
β−
 radiation, the emission of a fast electron from the nucleus (the accompanying antineutrino is omitted). In the Rutherford model for the nucleus, red spheres were protons with positive charge and blue spheres were protons tightly bound to an electron with no net charge.
The inset shows beta decay of a free neutron as it is understood today; an electron and antineutrino are created in this process.

In the 1911 Rutherford model, the atom consisted of a small massive nucleus with positive charge surrounded by a much larger cloud of negatively charged electrons. This model had been developed from the extraordinary finding that alpha particles were on occasion scattered to high angle when passing through gold foil, indicating the alpha particles were occasionally reflecting from a small, but dense, component of atoms. Rutherford and others noted the disparity between the atomic number of an atom, or number of positive charges, and its mass computed in atomic mass units. The atomic number of an atom is usually about half its atomic mass. In 1920 Rutherford suggested that the disparity could be explained by the existence of a neutrally charged particle within the atomic nucleus.[5] Since at the time no such particle was known to exist, yet the mass of such a particle had to be about equal to that of the proton, Rutherford considered the required particle to be a neutral double consisting of an electron closely orbiting a proton.[5] The mass of protons is about 1800 times greater than that of electrons.

There were other motivations for the proton–electron model. As noted by Rutherford at the time, "We have strong reason for believing that the nuclei of atoms contain electrons as well as positively charged bodies...",[5] namely, it was known that beta radiation was electrons emitted from the nucleus.

Rutherford called these uncharged particles neutrons, apparently from the Latin root for neutral and the Greek ending -on (by imitation of electron and proton).[6][7] References to the word neutron in connection with the atom can be found in the literature as early as 1899, however.[8]

Problems of the nuclear electrons hypothesis

Throughout the 1920s, physicists assumed that the atomic nucleus was composed of protons and "nuclear electrons".[9][10] Under this hypothesis, the nitrogen-14 (14N) nucleus would be composed of 14 protons and 7 electrons, so that it would have a net charge of +7 elementary charge units and a mass of 14 atomic mass units. The nucleus was also orbited by another 7 electrons, termed "external electrons" by Rutherford,[5] to complete the 14N atom. The Rutherford model was very influential, however, motivating the Bohr model for electrons orbiting the nucleus in 1913 and eventually leading to quantum mechanics by the mid-1920s but there were obvious problems

By about 1930 it was generally recognized that it was difficult to reconcile the proton–electron model for nuclei with the Heisenberg uncertainty relation of quantum mechanics.[11][12] This relation, Δx⋅Δp ≥ ½ħ, implies that an electron confined to a region the size of an atomic nucleus has an expected kinetic energy of 10–100 MeV.[12][13][14] This energy is larger than the binding energy of nucleons[clarification needed] and larger than the observed energy of beta particles emitted from the nucleus.[12] While these considerations did not "prove" an electron could not exist in the nucleus, they were challenging for physicists to interpret. Indeed, Heisenberg at one time considered the possibility that the uncertainty relation was not applicable inside the nuclei.[15]

The Klein paradox,[16] discovered by Oskar Klein in 1928, presented further quantum mechanical objections to the notion of an electron confined within a nucleus.[11] Derived from the Dirac equation, this clear and precise paradox showed that a high-energy electron approaching a potential barrier has a high probability of passing through the barrier, or escaping, by transforming to a particle of negative mass. Apparently, an electron could not be confined within a nucleus by any potential well. The meaning of this paradox was intensely debated at the time.[11]

Observations of the energy levels of atoms and molecules were inconsistent with the nuclear spin expected from proton–electron hypothesis. Molecular spectroscopy of dinitrogen (14N2) showed that transitions originating from even rotational levels are more intense than those from odd levels, hence the even levels are more populated. According to quantum mechanics and the Pauli exclusion principle, the spin of the 14N nucleus is therefore an integer multiple of ħ (the reduced Planck constant).[17][18] Yet both protons and electrons carry an intrinsic spin of ½ ħ, and there is no way to arrange an odd number (14 protons + 7 electrons = 21) of spins ±½ ħ to give a spin that is an integer multiple of ħ.

The observed hyperfine structure of atomic spectra was inconsistent with the proton–electron hypothesis. This structure is caused by the influence of the nucleus on the dynamics of orbiting electrons. The magnetic moments of supposed "nuclear electrons" should produce hyperfine spectral line splittings similar to the Zeeman effect , but no such effects were observed.[11] This contradiction was somewhat mysterious,[9] until it was realized that there are no individual nuclear electrons in the nucleus.

Discovery of the neutron

In 1931, Walther Bothe and Herbert Becker in Giessen, Germany found that if the very energetic alpha particles emitted from polonium fell on certain light elements, specifically beryllium, boron, or lithium, an unusually penetrating radiation was produced. Since this radiation was not influenced by an electric field (neutrons have no charge), it was thought to be gamma radiation. The radiation was more penetrating than any gamma rays known, and the details of experimental results were difficult to interpret.[19][20] The following year Irène Joliot-Curie and Frédéric Joliot in Paris showed that if this unknown radiation fell on paraffin, or any other hydrogen-containing compound, it ejected protons of very high energy.[21] This observation was not in itself inconsistent with the assumed gamma ray nature of the new radiation, but detailed quantitative analysis of the data became increasingly difficult to reconcile with such a hypothesis. In Rome, the young physicist Ettore Majorana suggested that the manner in which the new radiation interacted with protons required a new neutral particle.[22]

On hearing of the Paris results in 1932, neither Rutherford nor James Chadwick at the Cavendish Laboratory in Cambridge were convinced by the gamma ray hypothesis.[23] Chadwick had searched for Rutherford's neutron by several experiments throughout the 1920s without success. Chadwick quickly performed a series of experiments showing that the gamma ray hypothesis was untenable. He repeated the creation of the radiation using beryllium, used better approaches to detection, and aimed the radiation at paraffin following the Paris experiment. Paraffin is high in hydrogen content, hence offers a target dense with protons; since neutrons and protons have almost equal mass, protons scatter energetically from neutrons. Chadwick measured the range of these protons, and also measured how the new radiation impacted the atoms of various gases.[24] He found that the new radiation consisted of not gamma rays, but uncharged particles with about the same mass as the proton; these particles were neutrons.[25][26] Chadwick won the Nobel Prize in Physics for this discovery in 1935.[27]

The year 1932 was later referred to as the "annus mirabilis" for nuclear physics in the Cavendish Laboratory,[24] with discoveries of the neutron, artificial nuclear disintegration by the Cockcroft–Walton particle accelerator, and the positron.

Proton–neutron model of the nucleus

Models depicting the nucleus and electron energy levels in hydrogen, helium, lithium, and neon atoms. In reality, the diameter of the nucleus is about 100,000 times smaller than the diameter of the atom.

Given the problems of the proton–electron model,[9][10] it was quickly accepted that the atomic nucleus is composed of protons and neutrons. Within months after the discovery of the neutron, Werner Heisenberg[28][29][30] and Dmitri Ivanenko[31] had proposed proton–neutron models for the nucleus.[32] Heisenberg's landmark papers approached the description of protons and neutrons in the nucleus through quantum mechanics. While Heisenberg's theory for protons and neutrons in the nucleus was a "major step toward understanding the nucleus as a quantum mechanical system,"[33] he still assumed the presence of nuclear electrons. In particular, Heisenberg assumed the neutron was a proton–electron composite, for which there is no quantum mechanical explanation. Heisenberg had no explanation for how lightweight electrons could be bound within the nucleus. Heisenberg introduced the first theory of nuclear exchange forces that bind the nucleons. He considered protons and neutrons to be different quantum states of the same particle, i.e., nucleons distinguished by the value of their nuclear isospin quantum numbers.

The proton–neutron model explained the puzzle of dinitrogen noticed independently by Ralph Kronig and Franco Rasetti.[12] When 14N was proposed to consist of 3 pairs each of protons and neutrons, with an additional unpaired neutron and proton each contributing a spin of 1⁄2 ħ in the same direction for a total spin of 1 ħ, the model became viable.[34][35][36] Soon, neutrons were used to naturally explain spin differences in many different nuclides in the same way.

If the proton–neutron model for the nucleus resolved many issues, it highlighted the problem of explaining the origins of beta radiation. No existing theory could account for how electrons could emanate from the nucleus. In 1934, Enrico Fermi published his classic paper describing the process of beta decay, in which the neutron decays to a proton by creating an electron and a (as yet undiscovered) neutrino.[37] The paper employed the analogy that photons, or electromagnetic radiation, were similarly created and destroyed in atomic processes. Ivanenko had suggested a similar analogy in 1932.[34][38] Fermi's theory requires the neutron to be a spin-½ particle. The theory preserved the principle of conservation of energy, which had been thrown into question by the continuous energy distribution of beta particles. The basic theory for beta decay proposed by Fermi was the first to show how particles could be created and destroyed. It established a general, basic theory for the interaction of particles by weak or strong forces.[37] While this influential paper has stood the test of time, the ideas within it were so new that when it was first submitted to the journal Nature in 1933 it was rejected as being too speculative.[33]

Seventh Solvay Conference, 1933.

The question of whether the neutron was a composite particle of a proton and an electron persisted for a few years after its discovery.[39][40] In 1932 Harrie Massey explored a model for a composite neutron to account for its great penetrating power through matter and its electrical neutrality,[41] for example. The issue was a legacy of the prevailing view from the 1920s that the only elementary particles were the proton and electron. The nature of the neutron was a primary topic of discussion at the 7th Solvay Conference held in October 1933, attended by Heisenberg, Niels Bohr, Lise Meitner, Ernest Lawrence, Fermi, Chadwick, and others.[33][42] As posed by Chadwick in his Bakerian Lecture in 1933, the primary question was the mass of the neutron relative to the proton. If the neutron's mass was less than the combined masses of a proton and an electron (1.0078 u), then the neutron could be a proton-electron composite because of the mass defect from the binding energy. If greater than the combined masses, then the neutron was elementary like the proton.[43] The question was challenging to answer because the electron's mass is only 0.05% of the proton's, hence precise measurements were required.

The difficulty of making the measurement is illustrated by the wide ranging values for the mass of the neutron obtained from 1932-1934. The accepted value today is 1.00866 u. In Chadwick's 1932 paper reporting on the discovery, he estimated the mass of the neutron to be between 1.005 u and 1.008 u.[23] By bombarding boron with alpha particles, Frédéric and Irène Joliot-Curie obtained a high value of 1.012 u, while Ernest Lawrence's team at the University of California measured the small value 1.0006 u using their new cyclotron.[44] The issue was resolved in 1935 when Chadwick and his doctoral student Maurice Goldhaber, reported the first accurate measurement of the mass of the neutron. They used the 2.6 MeV gamma rays of Thallium-208 (208Tl) (then known as thorium C") to photodisintegrate deuterium:

2
1D
 		 + 
γ
 		 →  1
1H
 		 + 
n

The energies of the resulting proton and neutron could be used to accurately determine the neutron's mass. Chadwick and Goldhaber found the neutron's mass to be slightly greater than the mass of the proton (1.0084 u or 1.0090 u, depending on precise values used for the proton and deuteron masses), and therefore, in support of Fermi's theory, predicted that an unbound neutron is unstable and would undergo beta decay.[45][46] The mass of the neutron was too large to be a proton-electron composite, and the neutron was therefore identified as an elementary particle.[23]

Neutron physics in the 1930s

See also: Neutron magnetic moment

Soon after the discovery of the neutron, indirect evidence suggested the neutron had an unexpected non-zero value for its magnetic moment. Attempts to measure the neutron's magnetic moment originated with the discovery by Otto Stern in 1933 in Hamburg that the proton had an anomalously large magnetic moment.[47][48] By 1934 groups led by Stern, now in Pittsburgh, and I. I. Rabi in New York had independently deduced that the magnetic moment of the neutron was negative and unexpectedly large by measuring the magnetic moments of the proton and deuteron.[40][49][50][51][52] Values for the magnetic moment of the neutron were also determined by Robert Bacher[53] (1933) at Ann Arbor and I.Y. Tamm and S.A. Altshuler[40][54] (1934) in the Soviet Union from studies of the hyperfine structure of atomic spectra. By the late 1930s accurate values for the magnetic moment of the neutron had been deduced by the Rabi group using measurements employing newly developed nuclear magnetic resonance techniques.[52] The large value for the proton's magnetic moment and the inferred negative value for the neutron's magnetic moment were unexpected and raised many questions.[40]

The discovery of the neutron immediately gave scientists a new tool for probing the properties of atomic nuclei. Alpha particles had been used over the previous decades in scattering experiments, but such particles, which are helium nuclei, have +2 charge. This charge makes it difficult for alpha particles to overcome the Coulomb repulsive force and interact directly with the nuclei of atoms. Since neutrons have no electric charge, they do not have to overcome this force to interact with nuclei. Almost coincident with its discovery, neutrons were used by Norman Feather, Chadwick's colleague and protege, in scattering experiments with nitrogen.[55] Feather was able to show that neutrons interacting with nitrogen nuclei scattered to protons or induced nitrogen to disintegrate to form boron with the emission of an alpha particle. Feather was therefore the first to show that neutrons produce nuclear disintegrations.

Fermi and his students (the Via Panisperna boys) in the courtyard of Rome University's Physics Institute in Via Panisperna, about 1934. From Left to right: Oscar D'Agostino, Emilio Segrè, Edoardo Amaldi, Franco Rasetti and Fermi

In Rome Enrico Fermi bombarded heavier elements with neutrons and found the products to be radioactive. By 1934 Fermi had used neutrons to induce radioactivity in 22 different elements, many of these elements of high atomic number. Noticing that other experiments with neutrons at his laboratory seemed to work better on a wooden table than a marble table, Fermi suspected that the protons of the wood were slowing the neutrons and so increasing the chance for the neutron to interact with nuclei. Fermi therefore passed neutrons through paraffin wax to slow them and found that the radioactivity of bombarded elements increased by a hundredfold. The cross section for interaction with nuclei is much larger for slow neutrons than for fast neutrons. In 1938 Fermi received the Nobel Prize in Physics "for his demonstrations of the existence of new radioactive elements produced by neutron irradiation, and for his related discovery of nuclear reactions brought about by slow neutrons".[56]

Lise Meitner and Otto Hahn in their laboratory.

Jointly with Lise Meitner and his pupil and assistant Fritz Strassmann, Otto Hahn furthered the research begun by Fermi and his team when he bombarded uranium with neutrons at his laboratory in Berlin. Between 1934 and 1938, Hahn, Meitner, and Strassmann found a great number of radioactive transmutation products from these experiments, all of which they regarded as transuranic.[57] The decisive experiment on 16–17 December 1938 (the celebrated "radium–barium–mesothorium–fractionation") produced puzzling results: the three isotopes consistently behaved not as radium, but as barium.[58] By January 1939 Hahn had concluded that he was seeing light platinoids, barium, lanthanum, and cerium. Hahn and his collaborators had observed the fractionation of uranium nuclei into light elements by neutron bombardment. Meitner, now in Sweden to escape antisemitic persecution in Nazi Germany, and her nephew Otto Frisch correctly interpreted these observations as nuclear fission, a term coined by Frisch.[59] In their second publication on nuclear fission, Hahn and Strassmann predicted the existence and liberation of additional neutrons during the fission process.[60] Frédéric Joliot and his team proved this phenomena to be a chain reaction in March 1939. In 1945 Hahn received the 1944 Nobel Prize in Chemistry "for his discovery of the fission of heavy atomic nuclei."[61][62][63]

The discovery of nuclear fission at the end of 1938 marked a shift in the centers of nuclear research from Europe to the United States. Large numbers of scientists were migrating to the United States to escape the troubles in Europe and the looming war (See Jewish scientists and the Manhattan Project). The new centers of nuclear research were the universities in the United States, particularly Columbia University in New York and the University of Chicago where Enrico Fermi had relocated, and a secret research facility at Los Alamos, New Mexico, established in 1942, the new home of the Manhattan project.

Nuclear fission caused by absorption of a neutron by uranium-235. The heavy nuclide fragments into lighter components and additional neutrons.
The Trinity test of the Manhattan Project in 1945 was the first atomic bomb.

See also

Wikimedia Commons has media related to Discovery of the neutron.

References

  1. ^ Campbell, John. "Rutherford – A Brief Biography". Rutherford.org.nz. Retrieved 4 March 2013.
  2. ^ E. Rutherford and T. Royds (1908) "Spectrum of the radium emanation," Philosophical Magazine, Series 6, vol. 16, pages 313–317.
  3. ^ Ernest Rutherford (1911). The scattering of alpha and beta particles by matter and the structure of the atom. Taylor & Francis. p. 688.
  4. ^ M. S. Longair (2003). Theoretical concepts in physics: an alternative view of theoretical reasoning in physics. Cambridge University Press. pp. 377–378. ISBN 978-0-521-52878-8.
  5. ^ a b c d E. Rutherford (1920). "Nuclear Constitution of Atoms". Proceedings of the Royal Society A. 97 (686): 374. Bibcode:1920RSPSA..97..374R. doi:10.1098/rspa.1920.0040.
  6. ^ Wolfgang Pauli (1985). "Das Jahr 1932 Die Entdeckung des Neutrons". Wolfgang Pauli Wissenschaftlicher Briefwechsel mit Bohr, Einstein, Heisenberg u.a. Sources in the History of Mathematics and Physical Sciences. Vol. 6. p. 105. doi:10.1007/978-3-540-78801-0_3. ISBN 978-3-540-13609-5.
  7. ^ Hendry, John, ed. (1984), Cambridge Physics in the Thirties, Adam Hilger Ltd, Bristol, ISBN 0852747616
  8. ^ N. Feather (1960). "A history of neutrons and nuclei. Part 1". Contemporary Physics. 1 (3): 191–203. Bibcode:1960ConPh...1..191F. doi:10.1080/00107516008202611.
  9. ^ a b c Brown, Laurie M. (1978). "The idea of the neutrino". Physics Today. 31 (9): 23. Bibcode:1978PhT....31i..23B. doi:10.1063/1.2995181.
  10. ^ a b Friedlander G., Kennedy J.W. and Miller J.M. (1964) Nuclear and Radiochemistry (2nd edition), Wiley, pp. 22–23 and 38–39
  11. ^ a b c d Stuewer, Roger H. (1985). "Niels Bohr and Nuclear Physics". In French, A. P.; Kennedy, P. J. (eds.). Niels Bohr: A Centenary Volume. Harvard University Press. pp. 197–220. ISBN 0674624165.
  12. ^ a b c d Pais, Abraham (1986). Inward Bound. Oxford: Oxford University Press. p. 299. ISBN 0198519974.
  13. ^ Shultis, J. Kenneth; Faw, Richard E. (2007), Fundamentals of Nuclear Science and Engineering, CRC, 2nd edition, ISBN 1420051369
  14. ^ In a nucleus of diameter R in the order of 10 fm, the uncertainty principle would require an electron to have a momentum p of the order of h/R. Such a momentum implies that the electron has a (relativistic) kinetic energy of 10–100 MeV.
  15. ^ Tomonaga, chapter 9
  16. ^ Klein, O. (1929). "Die Reflexion von Elektronen an einem Potentialsprung nach der relativistischen Dynamik von Dirac". Zeitschrift für Physik. 53 (3–4): 157. Bibcode:1929ZPhy...53..157K. doi:10.1007/BF01339716.
  17. ^ Atkins, P.W. and J. de Paula, P.W. (2006) "Atkins' Physical Chemistry" (8th edition), W.H. Freeman, p. 451
  18. ^ Herzberg, G. (1950) Spectra of Diatomic Molecules (2nd edition), van Nostrand Reinhold, pp. 133–140
  19. ^ Bothe, W.; Becker, H. (1930). "Künstliche Erregung von Kern-γ-Strahlen". Zeitschrift für Physik. 66 (5–6): 289. Bibcode:1930ZPhy...66..289B. doi:10.1007/BF01390908. {{cite journal}}: Unknown parameter |trans_title= ignored (|trans-title= suggested) (help)
  20. ^ Becker, H.; Bothe, W. (1932). "Die in Bor und Beryllium erregten γ-Strahlen". Zeitschrift für Physik. 76 (7–8): 421. Bibcode:1932ZPhy...76..421B. doi:10.1007/BF01336726. {{cite journal}}: Unknown parameter |trans_title= ignored (|trans-title= suggested) (help)
  21. ^ Joliot-Curie, Irène; Joliot, Frédéric (1932). "Émission de protons de grande vitesse par les substances hydrogénées sous l'influence des rayons γ très pénétrants". Comptes Rendus. 194: 273. {{cite journal}}: Unknown parameter |trans_title= ignored (|trans-title= suggested) (help)
  22. ^ Ettore Majorana: genius and mystery, CERN courier.
  23. ^ a b c Brown, A. (1997). The Neutron and the Bomb: A Biography of Sir James Chadwick. Oxford University Press. ISBN 9780198539926.
  24. ^ a b "Atop the Physics Wave: Rutherford Back in Cambridge, 1919–1937". Rutherford's Nuclear World. American Institute of Physics. 2011–2014. Retrieved 19 August 2014.
  25. ^ Chadwick, James (1932). "Possible Existence of a Neutron". Nature. 129 (3252): 312. Bibcode:1932Natur.129Q.312C. doi:10.1038/129312a0.
  26. ^ Chadwick, J. (1933). "Bakerian Lecture. The Neutron". Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences. 142 (846): 1. Bibcode:1933RSPSA.142....1C. doi:10.1098/rspa.1933.0152.
  27. ^ 1935 Nobel Prize in Physics. Nobelprize.org. Retrieved on 2012-08-16.
  28. ^ Heisenberg, W. (1932). "Über den Bau der Atomkerne. I". Z. Phys. 77: 1–11. Bibcode:1932ZPhy...77....1H. doi:10.1007/BF01342433.
  29. ^ Heisenberg, W. (1932). "Über den Bau der Atomkerne. II". Z. Phys. 78 (3–4): 156–164. Bibcode:1932ZPhy...78..156H. doi:10.1007/BF01337585.
  30. ^ Heisenberg, W. (1933). "Über den Bau der Atomkerne. III". Z. Phys. 80 (9–10): 587–596. Bibcode:1933ZPhy...80..587H. doi:10.1007/BF01335696.
  31. ^ Iwanenko, D.D., The neutron hypothesis, Nature 129 (1932) 798.
  32. ^ Miller A. I. Early Quantum Electrodynamics: A Sourcebook, Cambridge University Press, Cambridge, 1995, ISBN 0521568919, pp. 84–88.
  33. ^ a b c Brown, L.M.; Rechenberg, H. (1996). The Origin of the Concept of Nuclear Forces. Bristol and Philadelphia: Institute of Physics Publishing. ISBN 0750303735.
  34. ^ a b Iwanenko, D. (1932). "Sur la constitution des noyaux atomiques". Compt. Rend. Acad Sci. Paris. 195: 439–441.
  35. ^ Bacher, R.F.; Condon, E.U. (1932). "The Spin of the Neutron". Physical Review. 41 (5): 683–685. Bibcode:1932PhRv...41..683G. doi:10.1103/PhysRev.41.683.
  36. ^ Whaling, W. (2009). "Robert F. Bacher 1905–2004" (PDF). Biographical Memoirs of the National Academy of Sciences.
  37. ^ a b Wilson, Fred L. (1968). "Fermi's Theory of Beta Decay". Am. J. Phys. 36 (12): 1150–1160. Bibcode:1968AmJPh..36.1150W. doi:10.1119/1.1974382.
  38. ^ Iwanenko, D. (1932). "Neutronen und kernelektronen". Physikalische Zeitschrift der Sowjetunion. 1: 820–822.
  39. ^ Kurie, F.N.D. (1933). "The Collisions of Neutrons with Protons". Physical Review. 44 (6): 463. Bibcode:1933PhRv...44..463K. doi:10.1103/PhysRev.44.463.
  40. ^ a b c d Breit, G.; Rabi, I.I. (1934). "On the interpretation of present values of nuclear moments". Physical Review. 46 (3): 230. Bibcode:1934PhRv...46..230B. doi:10.1103/PhysRev.46.230.
  41. ^ http://rspa.royalsocietypublishing.org/content/royprsa/138/835/460.full.pdf
  42. ^ Sime, R.L. (1996). Lise Meitner: A Life in Physics. University of California Press. ISBN 0520089065.
  43. ^ Chadwick, J. (1933). "Bakerian Lecture - The Neutron". Proc. Roy. Soc. 142 (846): 1–25. Bibcode:1933RSPSA.142....1C. doi:10.1098/rspa.1933.0152.
  44. ^ Seidel, R.W. (1989). Lawrence and his Laboratory: A History of the Lawrence Berkeley Laboratory. University of California Press. ISBN 9780520064263.
  45. ^ Chadwick, J.; Goldhaber, M. (1934). "A nuclear photo-effect: disintegration of the diplon by gamma rays". Nature. 134 (3381): 237–238. Bibcode:1934Natur.134..237C. doi:10.1038/134237a0.
  46. ^ Chadwick, J.; Goldhaber, M. (1935). "A nuclear photoelectric effect". Proc. R. Soc. Lond. 151 (873): 479–493. Bibcode:1935RSPSA.151..479C. doi:10.1098/rspa.1935.0162.
  47. ^ Frisch, R.; Stern, O. (1933). "Über die magnetische Ablenkung von Wasserstoffmolekülen und das magnetische Moment des Protons. I / Magnetic Deviation of Hydrogen Molecules and the Magnetic Moment of the Proton. I." Z. Phys. 84: 4–16. Bibcode:1933ZPhy...85....4F. doi:10.1007/bf01330773.
  48. ^ Esterman, I.; Stern, O. (1933). "Über die magnetische Ablenkung von Wasserstoffmolekülen und das magnetische Moment des Protons. II / Magnetic Deviation of Hydrogen Molecules and the Magnetic Moment of the Proton. I." Z. Phys. 85: 17–24. Bibcode:1933ZPhy...85...17E. doi:10.1007/BF01330774.
  49. ^ Esterman, I.; Stern, O. (1934). "Magnetic moment of the deuton". Physical Review. 45: 761(A109).
  50. ^ Rabi, I.I.; Kellogg, J.M.; Zacharias, J.R. (1934). "The magnetic moment of the proton". Physical Review. 46 (3): 157. Bibcode:1934PhRv...46..157R. doi:10.1103/PhysRev.46.157.
  51. ^ Rabi, I.I.; Kellogg, J.M.; Zacharias, J.R. (1934). "The magnetic moment of the deuton". Physical Review. 46 (3): 163. Bibcode:1934PhRv...46..163R. doi:10.1103/PhysRev.46.163.
  52. ^ a b John S. Rigden (2000). Rabi, Scientist and Citizen. Harvard University Press. ISBN 9780674004351.
  53. ^ Bacher, R.F. (1933). "Note on the Magnetic Moment of the Nitrogen Nucleus". Physical Review. 43 (12): 1001. Bibcode:1933PhRv...43.1001B. doi:10.1103/PhysRev.43.1001. Retrieved 2015-02-10.
  54. ^ Tamm, I.Y.; Altshuler, S.A. (1934). "Magnetic Moment of the Neutron". Doklady Akad. Nauk SSSR. 8: 455. Retrieved 2015-01-30.
  55. ^ N. Feather (1 June 1932). "The Collisions of Neutrons with Nitrogen Nuclei" (PDF). Proceedings of the Royal Society A. 136 (830): 709–727. Bibcode:1932RSPSA.136..709F. doi:10.1098/rspa.1932.0113.
  56. ^ Cooper, Dan (1999). Enrico Fermi: And the Revolutions in Modern physics. New York: Oxford University Press. ISBN 0-19-511762-X. OCLC 39508200. {{cite book}}: Invalid |ref=harv (help)
  57. ^ Hahn, O. (1958). "The Discovery of Fission". Scientific American. 198 (2): 76. doi:10.1038/scientificamerican0258-76.
  58. ^ Rife, Patricia (1999). Lise Meitner and the dawn of the nuclear age. Basel, Switzerland: Birkhäuser. ISBN 0-8176-3732-X.
  59. ^ Meitner, L.; Frisch, O. R. (1939). "Disintegration of Uranium by Neutrons: A New Type of Nuclear Reaction". Nature. 143 (3615): 239. Bibcode:1939Natur.143..239M. doi:10.1038/143239a0.
  60. ^ Hahn, O.; Strassmann, F. (10 February 1939). "Proof of the Formation of Active Isotopes of Barium from Uranium and Thorium Irradiated with Neutrons; Proof of the Existence of More Active Fragments Produced by Uranium Fission". Die Naturwissenschaften. 27 (6): 89–95. Bibcode:1939NW.....27...89H. doi:10.1007/BF01488988.
  61. ^ "The Nobel Prize in Chemistry 1944". Nobel Foundation. Retrieved 2007-12-17.
  62. ^ Bernstein, Jeremy (2001). Hitler's uranium club: the secret recordings at Farm Hall. New York: Copernicus. p. 281. ISBN 0-387-95089-3.
  63. ^ "The Nobel Prize in Chemistry 1944: Presentation Speech". Nobel Foundation. Retrieved 2008-01-03.

Further reading

Retrieved from "https://en.wikipedia.org/w/index.php?title=Discovery_of_the_neutron&oldid=751752802"