Temporal paradox
A temporal paradox, time paradox, or time travel paradox, is a paradox, an apparent contradiction, or logical contradiction associated with the idea of time travel or other foreknowledge of the future. While the notion of time travel to the future complies with the current understanding of physics via relativistic time dilation, temporal paradoxes arise from circumstances involving hypothetical time travel to the past – and are often used to demonstrate its impossibility.
Types[edit]
Temporal paradoxes fall into three broad groups: bootstrap paradoxes, consistency paradoxes, and Newcomb's paradox.[1] Bootstrap paradoxes violate causality by allowing future events to influence the past and cause themselves, or "bootstrapping", which derives from the idiom "pull oneself up by one's bootstraps."[2][3] Consistency paradoxes, on the other hand, are those where future events influence the past to cause an apparent contradiction, exemplified by the grandfather paradox, where a person travels to the past to kill their grandfather.[4] Newcomb's paradox stems from the apparent contradictions that stem from the assumptions of both free will and foreknowledge of future events. All of these are sometimes referred to individually as "causal loops." The term "time loop" is sometimes referred to as a causal loop,[2] but although they appear similar, causal loops are unchanging and self-originating, whereas time loops are constantly resetting.[5]
Bootstrap paradox[edit]
A boot-strap paradox, also known as an information loop, an information paradox,[6] an ontological paradox,[7] or a "predestination paradox" is a paradox of time travel that occurs when any event, such as an action, information, an object, or a person, ultimately causes itself, as a consequence of either retrocausality or time travel.[8][9][10][11]
Backward time travel would allow information, people, or objects whose histories seem to "come from nowhere".[8] Such causally looped events then exist in spacetime, but their origin cannot be determined.[8][9] The notion of objects or information that are "self-existing" in this way is often viewed as paradoxical.[9][6][12] Everett gives the movie Somewhere in Time as an example involving an object with no origin: an old woman gives a watch to a playwright who later travels back in time and meets the same woman when she was young, and gives her the same watch that she will later give to him.[6] An example of information which "came from nowhere" is in the movie Star Trek IV: The Voyage Home, in which a 23rd-century engineer travels back in time, and gives the formula for transparent aluminum to the 20th-century engineer who supposedly invented it.
Predestination paradox[edit]
Smeenk uses the term "predestination paradox" to refer specifically to situations in which a time traveler goes back in time to try to prevent some event in the past.[7]
Grandfather paradox[edit]
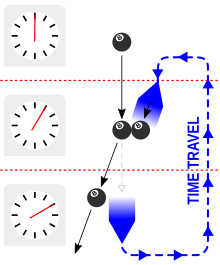
The consistency paradox or grandfather paradox occurs when the past is changed in any way, thus creating a contradiction. A common example given is traveling to the past and intervening with the conception of one's ancestors (such as causing the death of the parent beforehand), thus affecting the conception of oneself. If the time traveler were not born, then it would not be possible for them to undertake such an act in the first place. Therefore, the ancestor lives to offspring the time traveler's next-generation ancestor, and eventually the time traveler. There is thus no predicted outcome to this.[8] Consistency paradoxes occur whenever changing the past is possible.[9] A possible resolution is that a time traveller can do anything that did happen, but cannot do anything that did not happen. Doing something that did not happen results in a contradiction.[8] This is referred to as the Novikov self-consistency principle.
Variants[edit]
The grandfather paradox encompasses any change to the past,[13] and it is presented in many variations, including killing one's past self.[14][15] Both the "retro-suicide paradox" and the "grandfather paradox" appeared in letters written into Amazing Stories in the 1920s.[16] Another variant of the grandfather paradox is the "Hitler paradox" or "Hitler's murder paradox", in which the protagonist travels back in time to murder Adolf Hitler before he can instigate World War II and the Holocaust. Rather than necessarily physically preventing time travel, the action removes any reason for the travel, along with any knowledge that the reason ever existed.[17]
Physicist John Garrison et al. give a variation of the paradox of an electronic circuit that sends a signal through a time machine to shut itself off, and receives the signal before it sends it.[18][19]
Newcomb's paradox[edit]
Newcomb's paradox is a thought experiment showing an apparent contradiction between the expected utility principle and the strategic dominance principle.[20]
The thought experiment is often extended to explore causality and free will by allowing for "perfect predictors": if perfect predictors of the future exist, for example if time travel exists as a mechanism for making perfect predictions, then perfect predictions appear to contradict free will because decisions apparently made with free will are already known to the perfect predictor.[21][22] Predestination does not necessarily involve a supernatural power, and could be the result of other "infallible foreknowledge" mechanisms.[23] Problems arising from infallibility and influencing the future are explored in Newcomb's paradox.[24]
Proposed resolutions[edit]
Logical impossibility[edit]
Even without knowing whether time travel to the past is physically possible, it is possible to show using modal logic that changing the past results in a logical contradiction. If it is necessarily true that the past happened in a certain way, then it is false and impossible for the past to have occurred in any other way. A time traveler would not be able to change the past from the way it is; they would only act in a way that is already consistent with what necessarily happened.[25][26]
Consideration of the grandfather paradox has led some to the idea that time travel is by its very nature paradoxical and therefore logically impossible. For example, the philosopher Bradley Dowden made this sort of argument in the textbook Logical Reasoning, arguing that the possibility of creating a contradiction rules out time travel to the past entirely. However, some philosophers and scientists believe that time travel into the past need not be logically impossible provided that there is no possibility of changing the past,[13] as suggested, for example, by the Novikov self-consistency principle. Dowden revised his view after being convinced of this in an exchange with the philosopher Norman Swartz.[27]
Illusory time[edit]
Consideration of the possibility of backward time travel in a hypothetical universe described by a Gödel metric led famed logician Kurt Gödel to assert that time might itself be a sort of illusion.[28][29] He suggests something along the lines of the block time view, in which time is just another dimension like space, with all events at all times being fixed within this four-dimensional "block".[citation needed]
Physical impossibility[edit]
Sergey Krasnikov writes that these bootstrap paradoxes – information or an object looping through time – are the same; the primary apparent paradox is a physical system evolving into a state in a way that is not governed by its laws.[30]: 4 He does not find these paradoxical and attributes problems regarding the validity of time travel to other factors in the interpretation of general relativity.[30]: 14–16
Self-sufficient loops[edit]
A 1992 paper by physicists Andrei Lossev and Igor Novikov labeled such items without origin as Jinn, with the singular term Jinnee.[31]: 2311–2312 This terminology was inspired by the Jinn of the Quran, which are described as leaving no trace when they disappear.[32]: 200–203 Lossev and Novikov allowed the term "Jinn" to cover both objects and information with the reflexive origin; they called the former "Jinn of the first kind", and the latter "Jinn of the second kind".[6][31]: 2315–2317 [32]: 208 They point out that an object making circular passage through time must be identical whenever it is brought back to the past, otherwise it would create an inconsistency; the second law of thermodynamics seems to require that the object tends to a lower energy state throughout its history, and such objects that are identical in repeating points in their history seem to contradict this, but Lossev and Novikov argued that since the second law only requires entropy to increase in closed systems, a Jinnee could interact with its environment in such a way as to regain "lost" entropy.[6][32]: 200–203 They emphasize that there is no "strict difference" between Jinn of the first and second kind.[31]: 2320 Krasnikov equivocates between "Jinn", "self-sufficient loops", and "self-existing objects", calling them "lions" or "looping or intruding objects", and asserts that they are no less physical than conventional objects, "which, after all, also could appear only from either infinity or a singularity."[30]: 8–9
Novikov self-consistency principle[edit]
The self-consistency principle developed by Igor Dmitriyevich Novikov[33]: p. 42 note 10 expresses one view as to how backward time travel would be possible without the generation of paradoxes. According to this hypothesis, even though general relativity permits some exact solutions that allow for time travel[34] that contain closed timelike curves that lead back to the same point in spacetime,[35] physics in or near closed timelike curves (time machines) can only be consistent with the universal laws of physics, and thus only self-consistent events can occur. Anything a time traveler does in the past must have been part of history all along, and the time traveler can never do anything to prevent the trip back in time from happening, since this would represent an inconsistency. The authors concluded that time travel need not lead to unresolvable paradoxes, regardless of what type of object was sent to the past.[36]
Physicist Joseph Polchinski considered a potentially paradoxical situation involving a billiard ball that is fired into a wormhole at just the right angle such that it will be sent back in time and collides with its earlier self, knocking it off course, which would stop it from entering the wormhole in the first place. Kip Thorne referred to this problem as "Polchinski's paradox".[36] Thorne and two of his students at Caltech, Fernando Echeverria and Gunnar Klinkhammer, went on to find a solution that avoided any inconsistencies, and found that there was more than one self-consistent solution, with slightly different angles for the glancing blow in each case.[37] Later analysis by Thorne and Robert Forward showed that for certain initial trajectories of the billiard ball, there could be an infinite number of self-consistent solutions.[36] It is plausible that there exist self-consistent extensions for every possible initial trajectory, although this has not been proven.[38]: 184 The lack of constraints on initial conditions only applies to spacetime outside of the chronology-violating region of spacetime; the constraints on the chronology-violating region might prove to be paradoxical, but this is not yet known.[38]: 187–188
Novikov's views are not widely accepted. Visser views causal loops and Novikov's self-consistency principle as an ad hoc solution, and supposes that there are far more damaging implications of time travel.[39] Krasnikov similarly finds no inherent fault in causal loops but finds other problems with time travel in general relativity.[30]: 14–16 Another conjecture, the cosmic censorship hypothesis, suggests that every closed timelike curve passes through an event horizon, which prevents such causal loops from being observed.[40]
Parallel universes[edit]
The interacting-multiple-universes approach is a variation of the many-worlds interpretation of quantum mechanics that involves time travelers arriving in a different universe than the one from which they came; it has been argued that, since travelers arrive in a different universe's history and not their history, this is not "genuine" time travel.[41] Stephen Hawking has argued for the chronology protection conjecture, that even if the MWI is correct, we should expect each time traveler to experience a single self-consistent history so that time travelers remain within their world rather than traveling to a different one.[42]
David Deutsch has proposed that quantum computation with a negative delay—backward time travel—produces only self-consistent solutions, and the chronology-violating region imposes constraints that are not apparent through classical reasoning.[43] However Deutsch's self-consistency condition has been demonstrated as capable of being fulfilled to arbitrary precision by any system subject to the laws of classical statistical mechanics, even if it is not built up by quantum systems.[44] Allen Everett has also argued that even if Deutsch's approach is correct, it would imply that any macroscopic object composed of multiple particles would be split apart when traveling back in time, with different particles emerging in different worlds.[45]
See also[edit]
- Quantum mechanics of time travel
- Fermi paradox
- Cosmic censorship hypothesis
- Retrocausality
- Wormhole
- Causality
- Causal structure
- Chronology protection conjecture
- Münchhausen trilemma
- Time loop
- Time travel in fiction
- Time travel
References[edit]
- ^ Jan Faye (November 18, 2015), "Backward Causation", Stanford Encyclopedia of Philosophy, retrieved May 25, 2019
- ^ a b Klosterman, Chuck (2009). Eating the Dinosaur (1st Scribner hardcover ed.). New York: Scribner. pp. 60–62. ISBN 9781439168486.
- ^ Ross, Kelley L. (1997). "Time Travel Paradoxes". Archived from the original on January 18, 1998.
- ^ Francisco Lobo (2003). "Time, Closed Timelike Curves and Causality". Nato Science Series II. 95: 289–296. arXiv:gr-qc/0206078. Bibcode:2003ntgp.conf..289L.
- ^ Jones, Matthew; Ormrod, Joan (2015). Time Travel in Popular Media. McFarland & Company. p. 207. ISBN 9780786478071.
- ^ a b c d e Everett, Allen; Roman, Thomas (2012). Time Travel and Warp Drives. Chicago: University of Chicago Press. pp. 136–139. ISBN 978-0-226-22498-5.
- ^ a b Smeenk, Chris; Wüthrich, Christian (2011), "Time Travel and Time Machines", in Callender, Craig (ed.), The Oxford Handbook of Philosophy of Time, Oxford University Press, p. 581, ISBN 978-0-19-929820-4
- ^ a b c d e Smith, Nicholas J.J. (2013). "Time Travel". Stanford Encyclopedia of Philosophy. Retrieved June 13, 2015.
- ^ a b c d Lobo, Francisco (2003). "Time, Closed Timelike Curves and Causality". The Nature of Time: Geometry, Physics and Perception. NATO Science Series II. Vol. 95. pp. 289–296. arXiv:gr-qc/0206078. Bibcode:2003ntgp.conf..289L. ISBN 1-4020-1200-4.
- ^ Rea, Michael (2014). Metaphysics: The Basics (1. publ. ed.). New York: Routledge. p. 78. ISBN 978-0-415-57441-9.
- ^ Rea, Michael C. (2009). Arguing about Metaphysics. New York [u.a.]: Routledge. p. 204. ISBN 978-0-415-95826-4.
- ^ Visser, Matt (1996). Lorentzian Wormholes: From Einstein to Hawking. New York: Springer-Verlag. p. 213. ISBN 1-56396-653-0.
- ^ a b Nicholas J.J. Smith (2013). "Time Travel". Stanford Encyclopedia of Philosophy. Retrieved November 2, 2015.
- ^ Horwich, Paul (1987). Asymmetries in Time: Problems in the Philosophy of Science (2nd ed.). Cambridge, Massachusetts: MIT Press. p. 116. ISBN 0262580888.
- ^ Jan Faye (November 18, 2015), "Backward Causation", Stanford Encyclopedia of Philosophy, retrieved May 25, 2019
- ^ Nahin, Paul J. (1999). Time Machines: Time Travel in Physics, Metaphysics, and Science Fiction (2nd ed.). New York: Springer-Verlag. ISBN 0-387-98571-9. Retrieved 2022-02-19.
- ^ Brennan, J.H. (1997). Time Travel: A New Perspective (1st ed.). Minnesota: Llewellyn Publications. p. 23. ISBN 9781567180855.
- ^ Garrison, J.C.; Mitchell, M.W.; Chiao, R.Y.; Bolda, E.L. (August 1998). "Superluminal Signals: Causal Loop Paradoxes Revisited". Physics Letters A. 245 (1–2): 19–25. arXiv:quant-ph/9810031. Bibcode:1998PhLA..245...19G. doi:10.1016/S0375-9601(98)00381-8. S2CID 51796022.
- ^ Nahin, Paul J. (2016). Time Machine Tales. Springer International Publishing. pp. 335–336. ISBN 9783319488622.
- ^ Wolpert, D. H.; Benford, G. (June 2013). "The lesson of Newcomb's paradox". Synthese. 190 (9): 1637–1646. doi:10.1007/s11229-011-9899-3. JSTOR 41931515. S2CID 113227.
- ^ Craig (1987). "Divine Foreknowledge and Newcomb's Paradox". Philosophia. 17 (3): 331–350. doi:10.1007/BF02455055. S2CID 143485859.
- ^ Craig, William Lane (1988). "Tachyons, Time Travel, and Divine Omniscience". The Journal of Philosophy. 85 (3): 135–150. doi:10.2307/2027068. JSTOR 2027068.
- ^ Craig, William Lane (1987). "Divine Foreknowledge and Newcomb's Paradox". Philosophia. 17 (3): 331–350. doi:10.1007/BF02455055. S2CID 143485859.
- ^ Dummett, Michael (1996). The Seas of Language. Oxford University Press. pp. 356, 370–375. ISBN 9780198240112.
- ^ Norman Swartz (2001), Beyond Experience: Metaphysical Theories and Philosophical Constraints, University of Toronto Press, pp. 226–227
- ^ Dummett, Michael (1996). The Seas of Language (New ed.). Oxford: Oxford University Press. pp. 368–369. ISBN 0198236212.
- ^ Norman Swartz (1993). "Time Travel - Visiting the Past". SFU.ca. Retrieved 2016-04-21.
- ^ Yourgrau, Palle (4 March 2009). A World Without Time: The Forgotten Legacy of Godel and Einstein. New York: Basic Books. p. 134. ISBN 9780786737000. Retrieved December 18, 2017.
- ^ Holt, Jim (2005-02-21). "Time Bandits". The New Yorker. Retrieved 2017-12-13.
- ^ a b c d Krasnikov, S. (2001), "The time travel paradox", Phys. Rev. D, 65 (6): 06401, arXiv:gr-qc/0109029, Bibcode:2002PhRvD..65f4013K, doi:10.1103/PhysRevD.65.064013, S2CID 18460829
- ^ a b c Lossev, Andrei; Novikov, Igor (15 May 1992). "The Jinn of the time machine: non-trivial self-consistent solutions" (PDF). Class. Quantum Gravity. 9 (10): 2309–2321. Bibcode:1992CQGra...9.2309L. doi:10.1088/0264-9381/9/10/014. S2CID 250912686. Archived from the original (PDF) on 17 November 2015. Retrieved 16 November 2015.
- ^ a b c Toomey, David (2012). The New Time Travelers. New York, New York: W. W. Norton & Company. ISBN 978-0-393-06013-3.
- ^ Friedman, John; Morris, Michael S.; Novikov, Igor D.; Echeverria, Fernando; Klinkhammer, Gunnar; Thorne, Kip S.; Yurtsever, Ulvi (1990). "Cauchy problem in spacetimes with closed timelike curves". Physical Review D. 42 (6): 1915–1930. Bibcode:1990PhRvD..42.1915F. doi:10.1103/PhysRevD.42.1915. PMID 10013039.
- ^ Krasnikov, S. (2002), "No time machines in classical general relativity", Classical and Quantum Gravity, 19 (15): 4109, arXiv:gr-qc/0111054, Bibcode:2002CQGra..19.4109K, doi:10.1088/0264-9381/19/15/316, S2CID 16517920
- ^ Gödel, Kurt (1949). "An Example of a New Type of Cosmological Solution of Einstein's Field Equations of Gravitation". Rev. Mod. Phys. 21 (3): 447–450. Bibcode:1949RvMP...21..447G. doi:10.1103/RevModPhys.21.447.
- ^ a b c Thorne, Kip S. (1994). Black Holes and Time Warps. W. W. Norton. pp. 509–513. ISBN 0-393-31276-3.
- ^ Echeverria, Fernando; Gunnar Klinkhammer; Kip Thorne (1991). "Billiard balls in wormhole spacetimes with closed timelike curves: Classical theory". Physical Review D. 44 (4): 1077–1099. Bibcode:1991PhRvD..44.1077E. doi:10.1103/PhysRevD.44.1077. PMID 10013968.
- ^ a b Earman, John (1995). Bangs, Crunches, Whimpers, and Shrieks: Singularities and Acausalities in Relativistic Spacetimes. Oxford University Press. ISBN 0-19-509591-X.
- ^ Nahin, Paul J. (1999). Time Machines: Time Travel in Physics, Metaphysics, and Science Fiction. American Institute of Physics. pp. 345–352. ISBN 0-387-98571-9.
- ^ Visser, Matt (15 April 1997). "Traversable wormholes: The Roman ring". Physical Review D. 55 (8): 5212–5214. arXiv:gr-qc/9702043. Bibcode:1997PhRvD..55.5212V. doi:10.1103/PhysRevD.55.5212. S2CID 2869291.
- ^ Frank Arntzenius; Tim Maudlin (December 23, 2009), "Time Travel and Modern Physics", Stanford Encyclopedia of Philosophy, retrieved May 25, 2019
- ^ Hawking, Stephen (1999). "Space and Time Warps". Archived from the original on February 10, 2012. Retrieved February 25, 2012.
- ^ Deutsch, David (15 November 1991). "Quantum mechanics near closed timelike lines". Physical Review D. 44 (10): 3197–3217. Bibcode:1991PhRvD..44.3197D. doi:10.1103/PhysRevD.44.3197. PMID 10013776.
- ^ Tolksdorf, Juergen; Verch, Rainer (2021). "The D-CTC condition is generically fulfilled in classical (non-quantum) statistical systems". Foundations of Physics. 51 (93): 93. arXiv:1912.02301. Bibcode:2021FoPh...51...93T. doi:10.1007/s10701-021-00496-z. S2CID 208637445.
- ^ Everett, Allen (2004). "Time travel paradoxes, path integrals, and the many worlds interpretation of quantum mechanics". Physical Review D. 69 (124023): 124023. arXiv:gr-qc/0410035. Bibcode:2004PhRvD..69l4023E. doi:10.1103/PhysRevD.69.124023. S2CID 18597824.
