Group delay and phase delay
In signal processing, group delay and phase delay are two related ways of describing how a signal's frequency components are delayed in time when passing through a linear time-invariant (LTI) system (such as a microphone, coaxial cable, amplifier, loudspeaker, telecommunications system, ethernet cable, digital filter, or analog filter). Phase delay describes the time shift of a sinusoidal component (a sine wave in steady state). Group delay describes the time shift of the envelope of a wave packet, a "pack" or "group" of oscillations centered around one frequency that travel together, formed for instance by multiplying (amplitude modulation) a sine wave by an envelope (such as a tapering function).
These delays are usually frequency dependent,[1] which means that different frequency components experience different delays. As a result, the signal's waveform experiences distortion as it passes through the system. This distortion can cause problems such as poor fidelity in analog video and analog audio, or a high bit-error rate in a digital bit stream. However, for the ideal case of a constant group delay across the entire frequency range of a bandlimited signal and flat frequency response, the waveform will experience no distortion.
Background[edit]
Frequency components of a signal[edit]
Fourier analysis reveals how signals in time can alternatively be expressed as the sum of sinusoidal frequency components, each based on the trigonometric function with a fixed amplitude and phase and no beginning and no end.
Linear time-invariant systems process each sinusoidal component independently; the property of linearity means they satisfy the superposition principle.
Introduction[edit]
The group delay and phase delay properties of a linear time-invariant (LTI) system are functions of frequency, giving the time from when a frequency component of a time varying physical quantity—for example a voltage signal—appears at the LTI system input, to the time when a copy of that same frequency component—perhaps of a different physical phenomenon—appears at the LTI system output.
A varying phase response as a function of frequency, from which group delay and phase delay can be calculated, typically occurs in devices such as microphones, amplifiers, loudspeakers, magnetic recorders, headphones, coaxial cables, and antialiasing filters.[2] All frequency components of a signal are delayed when passed through such devices, or when propagating through space or a medium, such as air or water.
While a phase response describes phase shift in angular units (such as degrees or radians), the phase delay is in units of time and equals the negative of the phase shift at each frequency divided by the value of that frequency. Group delay is the negative derivative of phase shift with respect to frequency.
Phase delay[edit]
A linear time-invariant system or device has a phase response property and a phase delay property, where one can be calculated exactly from the other. Phase delay directly measures the device or system time delay of individual sinusoidal frequency components in the steady state.[3] If the phase delay function at any given frequency—within a frequency range of interest—has the same constant of proportionality between the phase at a selected frequency and the selected frequency itself, the system/device will have the ideal of linear phase, which results in a constant group delay.[1] Since phase delay is a function of frequency giving time delay, a departure from the flatness of its function graph can reveal time delay differences among the various signal frequency components, in which case those differences will contribute to signal distortion, which is manifested as the output signal waveform shape being different from that of the input signal.
Group delay[edit]
While phase delay describes the system's response to steady state sinusoidal components, group delay describes the response to amplitude modulated sinusoids.
The group delay is a convenient measure of the linearity of the phase with respect to frequency in a modulation system.[4][5] For a modulation signal (passband signal), the information carried by the signal is carried exclusively in the wave envelope. Group delay therefore operates only with the frequency components derived from the envelope.
Basic modulation system[edit]

A device's group delay can be exactly calculated from the device's phase response, but not the other way around.
The simplest use case for group delay is illustrated in Figure 1 which shows a conceptual modulation system, which is itself an LTI system with a baseband output that is ideally an accurate copy of the baseband signal input. This system as a whole is referred to here as the outer LTI system/device, which contains an inner (red block) LTI system/device. As is often the case for a radio system, the inner red LTI system in Fig 1 can represent two LTI systems in cascade, for example an amplifier driving a transmitting antenna at the sending end and the other an antenna and amplifier at the receiving end.
Amplitude Modulation[edit]
Amplitude modulation creates the passband signal by shifting the baseband frequency components to a much higher frequency range. Although the frequencies are different, the passband signal carries the same information as the baseband signal. The demodulator does the inverse, shifting the passband frequencies back down to the original baseband frequency range. Ideally, the output (baseband) signal is a time delayed version of the input (baseband) signal where the waveform shape of the output is identical to that of the input.
In Figure 1, the outer system phase delay is the meaningful performance metric. For amplitude modulation, the inner red LTI device group delay becomes the outer LTI device phase delay. If the inner red device group delay is completely flat in the frequency range of interest, the outer device will have the ideal of a phase delay that is also completely flat, where the contribution of distortion due to the outer LTI device's phase response—determined entirely by the inner device's possibly different phase response—is eliminated. In that case, the group delay of the inner red device and the phase delay of the outer device give the same time delay figure for the signal as a whole, from the baseband input to the baseband output. It is significant to note that it is possible for the inner (red) device to have a very non-flat phase delay (but flat group delay), while the outer device has the ideal of a perfectly flat phase delay. This is fortunate because in LTI device design, a flat group delay is easier to achieve than a flat phase delay.
Angle Modulation[edit]
In an angle-modulation system—such as with frequency modulation (FM) or phase modulation (PM)—the (FM or PM) passband signal applied to an LTI system input can be analyzed as two separate passband signals, an in-phase (I) amplitude modulation AM passband signal and a quadrature-phase (Q) amplitude modulation AM passband signal, where their sum exactly reconstructs the original angle-modulation (FM or PM) passband signal. While the (FM/PM) passband signal is not amplitude modulation, and therefore has no apparent outer envelope, the I and Q passband signals do indeed have amplitude modulation envelopes. (However, unlike with regular amplitude modulation, the I and Q envelopes do not resemble the wave shape of the baseband signals, even though 100 percent of the baseband signal is represented in a complex manner by their envelopes.) So, for each of the I and Q passband signals, a flat group delay ensures that neither the I pass band envelope nor the Q passband envelope will have wave shape distortion, so when the I passband signal and the Q passband signal is added back together, the sum is the original FM/PM passband signal, which will also be unaltered.
Theory[edit]
According to LTI system theory (used in control theory and digital or analog signal processing), the output signal of an LTI system can be determined by convoluting the time-domain impulse response of the LTI system with the input signal . Linear time-invariant system § Fourier and Laplace transforms expresses this relationship as:
where denotes the convolution operation, and are the Laplace transforms of the input and impulse response , respectively, s is the complex frequency, and is the inverse Laplace transform. is called the transfer function of the LTI system and, like the impulse response , fully defines the input-output characteristics of the LTI system. This convolution can be evaluated by using the integral expression in the time domain, or (according to the rightmost expression) by using multiplication in the Laplace domain and then applying the inverse transform to return to time domain.
LTI system response to wave packet[edit]
Suppose that such a system is driven by a wave packet formed by a sinusoid multiplied by an amplitude envelope , so the input can be expressed in the following form:
Also suppose that the envelope is slowly changing relative to the sinusoid's frequency . This condition can be expressed mathematically as:
Applying the earlier convolution equation would reveal that the output of such an LTI system is very well approximated[clarification needed] as:
Here is the group delay and is the phase delay, and they are given by the expressions below (and potentially are functions of the angular frequency ). The phase of the sinusoid, as indicated by the positions of the zero crossings, is delayed in time by an amount equal to the phase delay, . The envelope of the sinusoid is delayed in time by the group delay, .
Mathematical definition of group delay and phase delay[edit]
The group delay, , and phase delay, , are (potentially) frequency-dependent[6] and can be computed from the unwrapped phase shift . The phase delay at each frequency equals the negative of the phase shift at that frequency divided by the value of that frequency:
The group delay at each frequency equals the negative of the slope (i.e. the derivative with respect to frequency) of the phase at that frequency:[7]
In a linear phase system (with non-inverting gain), both and are constant (i.e., independent of ) and equal, and their common value equals the overall delay of the system; and the unwrapped phase shift of the system (namely ) is negative, with magnitude increasing linearly with frequency .
LTI system response to complex sinusoid[edit]
More generally, it can be shown that for an LTI system with transfer function driven by a complex sinusoid of unit amplitude,
the output is
where the phase shift is
1st order low- or high-pass RC filter example[edit]
The phase of a 1st-order low-pass filter formed by a RC circuit with cutoff frequency is:[8]
Similarly, the phase for a 1st-order RC high-pass filter is:
Taking the negative derivative with respect to for either this low-pass or high-pass filter yields the same group delay of:[9]
For frequencies significantly lower than the cutoff frequency, the phase response is approximately linear (arctan for small inputs can be approximated as a line), so the group delay simplifies to a constant value of:
Similarly, right at the cutoff frequency,
As frequencies get even larger, the group delay decreases with the inverse square of the frequency and approaches zero as frequency approaches infinity.
Negative group delay[edit]
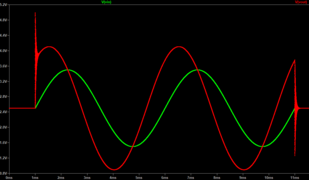
- Figure 2: Negative group delay filter circuit
-
Transient simulation of an input (green) wave whose output (red) is ahead by 1 ms, but with instability when the input turns on and off.
Filters will have negative group delay over frequency ranges where its phase response is positively-sloped. If a signal is band-limited within some maximum frequency B, then it is predictable to a small degree (within time periods smaller than 1⁄B). A filter whose group delay is negative over that signal's entire frequency range is able to use the signal's predictability to provide an illusion of a non-causal time advance. However, if the signal contains an unpredictable event (such as an abrupt change which makes the signal's spectrum exceed its band-limit), then the illusion breaks down.[10] Circuits with negative group delay (e.g., Figure 2) are possible, though causality is not violated.[11]
Negative group delay filters can be made in both digital and analog domains. Applications include compensating for the inherent delay of low-pass filters, to create zero phase filters, which can be used to quickly detect changes in the trends of sensor data or stock prices.[12]
Group delay in audio[edit]
Group delay has some importance in the audio field and especially in the sound reproduction field.[13][14] Many components of an audio reproduction chain, notably loudspeakers and multiway loudspeaker crossover networks, introduce group delay in the audio signal.[2][14] It is therefore important to know the threshold of audibility of group delay with respect to frequency,[15][16][17] especially if the audio chain is supposed to provide high fidelity reproduction. The best thresholds of audibility table has been provided by Blauert and Laws.[18]
| Frequency (kHz) |
Threshold (ms) |
Periods (Cycles) |
|---|---|---|
| 0.5 | 3.2 | 1.6 |
| 1 | 2 | 2 |
| 2 | 1 | 2 |
| 4 | 1.5 | 6 |
| 8 | 2 | 16 |
Flanagan, Moore and Stone conclude that at 1, 2 and 4 kHz, a group delay of about 1.6 ms is audible with headphones in a non-reverberant condition.[19] Other experimental results suggest that when the group delay in the frequency range from 300 Hz to 1 kHz is below 1.0 ms, it is inaudible.[16]
The waveform of any signal can be reproduced exactly by a system that has a flat frequency response and group delay over the bandwidth of the signal. Leach[20] introduced the concept of differential time-delay distortion, defined as the difference between the phase delay and the group delay:
- .
An ideal system should exhibit zero or negligible differential time-delay distortion.[20]
It is possible to use digital signal processing techniques to correct the group delay distortion that arises due to the use of crossover networks in multi-way loudspeaker systems.[21] This involves considerable computational modeling of loudspeaker systems in order to successfully apply delay equalization,[22] using the Parks-McClellan FIR equiripple filter design algorithm.[1][5][23][24]
Group delay in optics[edit]
Group delay is important in physics, and in particular in optics.
In an optical fiber, group delay is the transit time required for optical power, traveling at a given mode's group velocity, to travel a given distance. For optical fiber dispersion measurement purposes, the quantity of interest is group delay per unit length, which is the reciprocal of the group velocity of a particular mode. The measured group delay of a signal through an optical fiber exhibits a wavelength dependence due to the various dispersion mechanisms present in the fiber.
It is often desirable for the group delay to be constant across all frequencies; otherwise there is temporal smearing of the signal. Because group delay is , it therefore follows that a constant group delay can be achieved if the transfer function of the device or medium has a linear phase response (i.e., where the group delay is a constant). The degree of nonlinearity of the phase indicates the deviation of the group delay from a constant value.
The differential group delay is the difference in propagation time between the two eigenmodes X and Y polarizations. Consider two eigenmodes that are the 0° and 90° linear polarization states. If the state of polarization of the input signal is the linear state at 45° between the two eigenmodes, the input signal is divided equally into the two eigenmodes. The power of the transmitted signal ET,total is the combination of the transmitted signals of both x and y modes.
The differential group delay Dt is defined as the difference in propagation time between the eigenmodes: Dt = |tt,x − tt,y|.
True time delay[edit]
A transmitting apparatus is said to have true time delay (TTD) if the time delay is independent of the frequency of the electrical signal.[25][26] TTD allows for a wide instantaneous signal bandwidth with virtually no signal distortion such as pulse broadening during pulsed operation.
TTD is an important characteristic of lossless and low-loss, dispersion free, transmission lines. Telegrapher's equations § Lossless transmission reveals that signals propagate through them at a speed of for a distributed inductance L and capacitance C. Hence, any signal's propagation delay through the line simply equals the length of the line divided by this speed.
Group delay from transfer function polynomials[edit]
If a transfer function or Sij of a scattering parameter, is in a polynomial Laplace transform form, then the mathematical definition for group delay above may be solved analytically in closed form. A polynomial transfer function may be taken along the axis and defined as . may be determined from , and then the group delay may be determined by solving for .
to determine from , use the definition of . Given that is always real, and is always imaginary, may be redefined as where even and odd refer to the polynomials that contain only the even or odd order coefficients respectively. The in the numerator merely converts the imaginary numerator to a real value, since by itself is purely imaginary.
The above expressions contain four terms to calculate:
The equations above may be used to determine the group delay of polynomial in closed form, shown below after the equations have been reduced to a simplified form.
Polynomial ratio[edit]
A polynomial ratio of the form , such as that typically found in the definition of filter designs, may have the group delay determined by taking advantage of the phase relation, .
Simple filter example[edit]
A four pole Legendre filter transfer function used in the Legendre filter example is shown below.
The numerator group delay by inspection is zero, so only the denominator group delay need be determined.
Evaluating at = 1 rad/sec:
The group delay calculation procedure and results may be confirmed to be correct by comparing them to the results derived from the digital derivative of the phase angle, , using a small delta of +/-1.e-04 rad/sec.
Since he group delay calculated by the digital derivative using a small delta is within 7 digits of accuracy when compared to the precise analytical calculation, the group delay calculation procedure and results are confirmed to be correct.
Deviation from Linear Phase[edit]
Deviation from Linear Phase, , sometimes referred to as just, "phase deviation", is the difference between the phase response, , and the linear portion of the phase response ,[27] and is a useful measurement to determine the linearity of .
A convenient means to measure is to take the simple linear regression of sampled over a frequency range of interest, and subtract it from the actual . The of an ideal linear phase response would be expected to have a value of 0 across the frequency range of interest (such as the pass band of a filter), while the of a real-world approximately linear phase response may deviate from 0 by a small finite amount across the frequency range of interest.
Advantage over group delay[edit]
An advantage of measuring or calculating over measuring or calculating group delay, , is always converges to 0 as the phase becomes linear, whereas converges on a finite quantity that may not be known ahead of time. Given this, a linear phase optimizing function may more easily be executed with a goal than with a goal when the value for is not necessarily already known.
See also[edit]
- Audio system measurements
- Linear phase
- Bessel filter — low pass filter with maximally-flat group delay
- Legendre filter — from the example section
- Eye pattern
- Group velocity — "The group velocity of light in a medium is the inverse of the group delay per unit length."[28]
- Phase velocity
- Wave packet
References[edit]
![]() This article incorporates public domain material from Federal Standard 1037C. General Services Administration. Archived from the original on 2022-01-22.
This article incorporates public domain material from Federal Standard 1037C. General Services Administration. Archived from the original on 2022-01-22.
- ^ a b c Rabiner, Lawrence R.; Gold, Bernard (1975). Theory and Application of Digital Signal Processing. Englewood Cliffs, New Jersey: Prentice-Hall, Inc. ISBN 0-13-914101-4.
- ^ a b Preis, D. (1982). "Phase Distortion and Phase Equalization in Audio Signal Processing — A Tutorial Review". Journal of the Audio Engineering Society. 30 (11): 774–794. Retrieved 2022-05-22.
- ^ Lathi, B. P. (2005). Linear Systems and Signals (Second ed.). Oxford University Press, Inc. ISBN 978-0-19-515833-5.
- ^ Oppenheim, Alan V.; Schafer, R. W.; Buck, J. R. (1999). Discrete-Time Signal Processing. Upper Saddle River, New Jersey: Prentice-Hall, Inc. ISBN 0-13-754920-2.
- ^ a b Oppenheim, Alan V.; Schafer, Ronald W. (2014). Discrete-Time Signal Processing. England: Pearson Education Limited. ISBN 978-1-292-02572-8.
- ^ Ambardar, Ashok (1999). Analog and Digital Signal Processing (Second ed.). Cengage Learning. ISBN 9780534954093.
- ^ Oppenheim, Alan V.; Willsky, Alan S.; Nawab, Hamid (1997). Signals and Systems. Upper Saddle River, New Jersey: Prentice-Hall, Inc. ISBN 0-13-814757-4.
- ^ https://www.tedpavlic.com/teaching/osu/ece209/lab3_opamp_FO/lab3_opamp_FO_phase_shift.pdf
- ^ https://www.montana.edu/aolson/ee503/EELE503_filters.pdf page 11
- ^ Bariska, Andor (2008). "Negative Group Delay" (PDF). Physical Meaning of Negative Group Delay?. Archived (PDF) from the original on 2021-10-16. Retrieved 2022-10-28.
- ^ Nakanishi, Toshihiro; Sugiyama, K.; Kitano, M. (2002-01-01). "Demonstration of negative group delays in a simple electronic circuit". American Journal of Physics. 70 (11): 1117–1121. arXiv:quant-ph/0201001. Bibcode:2002AmJPh..70.1117N. doi:10.1119/1.1503378. S2CID 39928138.
- ^ Castor-Perry, Kendall (2020-03-18). "Five things to know about prediction and negative-delay filters". planetanalog.com. Archived from the original on 2022-06-28. Retrieved 2023-06-13.
- ^ Plomp, R.; Steeneken, H. J. M. (1969). "Effect of Phase on the Timbre of Complex Tones". The Journal of the Acoustical Society of America. 46 (2B): 409–421. Bibcode:1969ASAJ...46..409P. doi:10.1121/1.1911705. PMID 5804112.
- ^ a b Ashley, J. (1980). Group and phase delay requirements for loudspeaker systems. ICASSP '80. IEEE International Conference on Acoustics, Speech, and Signal Processing. Vol. 5. pp. 1030–1033. doi:10.1109/ICASSP.1980.1170852.
- ^ Möller, Henning (1975). "Loudspeaker phase measurements, transient response and audible quality" (PDF). Brüel & Kjaer (Application Note 17-198). Archived (PDF) from the original on 2022-10-09. Retrieved 2022-05-22.
- ^ a b Liski, J.; Mäkivirta, A.; Välimäki, V. (2018). Audibility of loudspeaker group-delay characteristics (PDF). 144th Audio Engineering Society International Convention, Paper Number 10008. Audio Engineering Society. pp. 879–888. Archived (PDF) from the original on 2022-10-09. Retrieved 2022-05-21.
- ^ Liski, Juho; Mäkivirta, Aki; Välimäki, Vesa (2021). "Audibility of Group-Delay Equalization". IEEE/ACM Transactions on Audio, Speech, and Language Processing. 29: 2189–2201. doi:10.1109/TASLP.2021.3087969. S2CID 236192266.
- ^ Blauert, J.; Laws, P. (May 1978). "Group Delay Distortions in Electroacoustical Systems" (PDF). Journal of the Acoustical Society of America. 63 (5): 1478–1483. Bibcode:1978ASAJ...63.1478B. doi:10.1121/1.381841. Archived from the original (PDF) on 2015-09-30.
- ^ Flanagan, Sheila; Moore, Brian C. J.; Stone, Michael A. (2005). "Discrimination of Group Delay in Clicklike Signals Presented via Headphones and Loudspeakers". Journal of the Audio Engineering Society. 53 (7/8): 593–611.
- ^ a b Leach, Jr., W. Marshall (1989). "The Differential Time-Delay Distortion and Differential Phase-Shift Distortion as Measures of Phase Linearity" (PDF). Journal of the Audio Engineering Society. 37 (9): 709–715. Archived (PDF) from the original on 2022-10-09.
- ^ Adam, Veronique; Benz, Sebastien (2007). Correction of Crossover Phase Distortion Using Reversed Time All-Pass IIR Filter. 122nd Audio Engineering Society Convention. Retrieved 2022-05-22.
- ^ Mäkivirta, Aki; Liski, Juho; Välimäki, Vesa (2018). "Modeling and Delay-Equalizing Loudspeaker Responses". Journal of the Audio Engineering Society. 66 (11): 922–934. doi:10.17743/jaes.2018.0053. S2CID 85506559. Retrieved 2022-05-22.
- ^ McClellan, J.; Parks, T.; Rabiner, L. (1973). "A computer program for designing optimum FIR linear phase digital filters". IEEE Transactions on Audio and Electroacoustics. 21 (6): 506–526. doi:10.1109/TAU.1973.1162525.
- ^ Oppenheim, Alan V.; Schafer, Ronald W. (2010). Discrete-Time Signal Processing. England: Pearson Education Limited. ISBN 978-0-13-198842-2.
- ^ "True Time Delay". Microwaves101, IEEE.
- ^ Julius O. Smith III. "Phase Delay and Group Delay". Music 320 Background Reader. Department of Electrical Engineering, Stanford University.
- ^ Keysight Technologies, Inc. (April 19, 2002). "Deviation from Linear Phase". Deviation from Linear Phase.
- ^ "Group Delay".




























































![{\displaystyle {\begin{aligned}&{\text{Group Delay}}=gd(T_{4}(j\omega ))=-{\frac {d\phi (\omega )}{d\omega }}\\&={\bigg [}0--{\frac {((-0.7870074*-0.548984)+(-1.1749977*-8.4434476))}{((-1.1749977)^{2}+(-0.7870074)^{2})}}{\bigg ]}\\&=5.1765430{\text{ sec}}\\&{\text{at }}\omega =1{\text{ rad/sec}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/080030fbdaaee01549039097e88196f01ae8353c)







