Heapsort
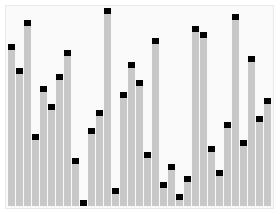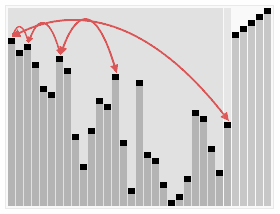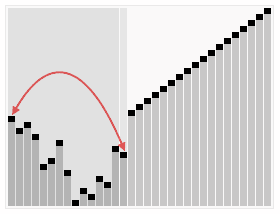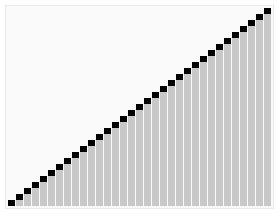 A run of heapsort sorting an array of randomly permuted values. In the first stage of the algorithm the array elements are reordered to satisfy the heap property. Before the actual sorting takes place, the heap tree structure is shown briefly for illustration. | |
| Class | Sorting algorithm |
|---|---|
| Data structure | Array |
| Worst-case performance | |
| Best-case performance | (distinct keys)[1][2] or (equal keys) |
| Average performance | |
| Worst-case space complexity | total auxiliary |
In computer science, heapsort is a comparison-based sorting algorithm which can be thought of as "an implementation of selection sort using the right data structure."[3] Like selection sort, heapsort divides its input into a sorted and an unsorted region, and it iteratively shrinks the unsorted region by extracting the largest element from it and inserting it into the sorted region. Unlike selection sort, heapsort does not waste time with a linear-time scan of the unsorted region; rather, heap sort maintains the unsorted region in a heap data structure to efficiently find the largest element in each step.
Although somewhat slower in practice on most machines than a well-implemented quicksort, it has the advantages of very simple implementation and a more favorable worst-case O(n log n) runtime. Most real-world quicksort variants include an implementation of heapsort as a fallback should they detect that quicksort is becoming degenerate. Heapsort is an in-place algorithm, but it is not a stable sort.
Heapsort was invented by J. W. J. Williams in 1964.[4] The paper also introduced the binary heap as a useful data structure in its own right.[5] In the same year, Robert W. Floyd published an improved version that could sort an array in-place, continuing his earlier research into the treesort algorithm.[5]
Overview
[edit]The heapsort algorithm can be divided into two phases: heap construction, and heap extraction.
The heap is an implicit data structure which takes no space beyond the array of objects to be sorted; the array is interpreted as a complete binary tree where each array element is a node and each node's parent and child links are defined by simple arithmetic on the array indexes. For a zero-based array, the root node is stored at index 0, and the nodes linked to node i are
iLeftChild(i) = 2⋅i + 1 iRightChild(i) = 2⋅i + 2 iParent(i) = floor((i−1) / 2)
where the floor function rounds down to the preceding integer. For a more detailed explanation, see Binary heap § Heap implementation.
This binary tree is a max-heap when each node is greater than or equal to both of its children. Equivalently, each node is less than or equal to its parent. This rule, applied throughout the tree, results in the maximum node being located at the root of the tree.
In the first phase, a heap is built out of the data (see Binary heap § Building a heap).
In the second phase, the heap is converted to a sorted array by repeatedly removing the largest element from the heap (the root of the heap), and placing it at the end of the array. The heap is updated after each removal to maintain the heap property. Once all objects have been removed from the heap, the result is a sorted array.
Heapsort is normally performed in place. During the first phase, the array is divided into an unsorted prefix and a heap-ordered suffix (initially empty). Each step shrinks the prefix and expands the suffix. When the prefix is empty, this phase is complete. During the second phase, the array is divided into a heap-ordered prefix and a sorted suffix (initially empty). Each step shrinks the prefix and expands the suffix. When the prefix is empty, the array is sorted.
Algorithm
[edit]The heapsort algorithm begins by rearranging the array into a binary max-heap. The algorithm then repeatedly swaps the root of the heap (the greatest element remaining in the heap) with its last element, which is then declared to be part of the sorted suffix. Then the heap, which was damaged by replacing the root, is repaired so that the greatest element is again at the root. This repeats until only one value remains in the heap.
The steps are:
- Call the
heapify()function on the array. This builds a heap from an array in O(n) operations. - Swap the first element of the array (the largest element in the heap) with the final element of the heap. Decrease the considered range of the heap by one.
- Call the
siftDown()function on the array to move the new first element to its correct place in the heap. - Go back to step (2) until the remaining array is a single element.
The heapify() operation is run once, and is O(n) in performance. The siftDown() function is called n times and requires O(log n) work each time, due to its traversal starting from the root node. Therefore, the performance of this algorithm is O(n + n log n) = O(n log n).
The heart of the algorithm is the siftDown() function. This constructs binary heaps out of smaller heaps, and may be thought of in two equivalent ways:
- given two binary heaps, and a shared parent node which is not part of either heap, merge them into a single larger binary heap; or
- given a "damaged" binary heap, where the max-heap property (no child is greater than its parent) holds everywhere except possibly between the root node and its children, repair it to produce an undamaged heap.
To establish the max-heap property at the root, up to three nodes must be compared (the root and its two children), and the greatest must be made the root. This is most easily done by finding the greatest child, then comparing that child to the root. There are three cases:
- If there are no children (the two original heaps are empty), the heap property trivially holds, and no further action is required.
- If root is greater than or equal to the greatest child, the heap property holds and likewise, no further action is required.
- If the root is less than the greatest child, exchange the two nodes. The heap property now holds at the newly-promoted node (it is greater than or equal to both of its children, and in fact greater than any descendant), but may be violated between the newly-demoted ex-root and its new children. To correct this, repeat the
siftDown()operation on the subtree rooted at the newly-demoted ex-root.
The number of iterations in any one siftdown() call is bounded by the height of the tree, which is ⌊log2 n⌋ = O(log n).
Pseudocode
[edit]The following is a simple way to implement the algorithm in pseudocode. Arrays are zero-based and swap is used to exchange two elements of the array. Movement 'down' means from the root towards the leaves, or from lower indices to higher. Note that during the sort, the largest element is at the root of the heap at a[0], while at the end of the sort, the largest element is in a[end].
procedure heapsort(a, count) is
input: an unordered array a of length count
(Build the heap in array a so that largest value is at the root)
heapify(a, count)
(The following loop maintains the invariants that a[0:end−1] is a heap, and
every element a[end:count−1] beyond end is greater than everything before it,
i.e. a[end:count−1] is in sorted order.)
end ← count
while end > 1 do
(the heap size is reduced by one)
end ← end − 1
(a[0] is the root and largest value. The swap moves it in front of the sorted elements.)
swap(a[end], a[0])
(the swap ruined the heap property, so restore it)
siftDown(a, 0, end)
The sorting routine uses two subroutines, heapify and siftDown. The former is the common in-place heap construction routine, while the latter is a common subroutine for implementing heapify.
(Put elements of 'a' in heap order, in-place)
procedure heapify(a, count) is
(start is initialized to the first leaf node)
(the last element in a 0-based array is at index count-1; find the parent of that element)
start ← iParent(count-1) + 1
while start > 0 do
(go to the last non-heap node)
start ← start − 1
(sift down the node at index 'start' to the proper place such that all nodes below
the start index are in heap order)
siftDown(a, start, count)
(after sifting down the root all nodes/elements are in heap order)
(Repair the heap whose root element is at index 'start', assuming the heaps rooted at its children are valid)
procedure siftDown(a, root, end) is
while iLeftChild(root) < end do (While the root has at least one child)
child ← iLeftChild(root) (Left child of root)
(If there is a right child and that child is greater)
if child+1 < end and a[child] < a[child+1] then
child ← child + 1
if a[root] < a[child] then
swap(a[root], a[child])
root ← child (repeat to continue sifting down the child now)
else
(The root holds the largest element. Since we may assume the heaps rooted
at the children are valid, this means that we are done.)
return
The heapify procedure operates by building small heaps and repeatedly merging them using siftDown. It starts with the leaves, observing that the they are trivial but valid heaps by themselves, and then adds parents. Starting with element n/2 and working backwards, each internal node is made the root of a valid heap by sifting down. The last step is sifting down the first element, after which the entire array obeys the heap property.
To see that this takes O(n) time, count the worst-case number of siftDown iterations. The last half of the array requires zero iterations, the preceding quarter requires at most one iteration, the eighth before that requires at most two iterations, the sixteenth before that requires at most three, and so on.
Looked at a different way, if we assume every siftDown call requires the maximum number of iterations, the first half of the array requires one iteration, the first quarter requires one more (total 2), the first eighth requires yet another (total 3), and so on.
This totals n/2 + n/4 + n/8 + ⋯ = n⋅(1/2 + 1/4 + 1/8 + ⋯), where the infinite sum is a well-known geometric series whose sum is 1, thus the product is simply n.
The above is an approximation. The exact worst-case number of comparisons during the heap-construction phase of heapsort is known to be equal to 2n − 2s2(n) − e2(n), where s2(n) is the number of 1 bits in the binary representation of n and e2(n) is the number of trailing 0 bits.[6][7]
Standard implementation
[edit]Although it is convenient to think of the two phases separately, most implementations combine the two, allowing a single instance of siftDownto be expanded inline.[8]: Algorithm H Two variables (here, start and end) keep track of the bounds of the heap area. The portion of the array before start is unsorted, while the portion beginning at end is sorted. Heap construction decreases start until it is zero, after which heap extraction decreases end until it is 1 and the array is entirely sorted.
procedure heapsort(a, count) is
input: an unordered array a of length count
start ← floor(count/2)
end ← count
while end > 1 do
if start > 0 then (Heap construction)
start ← start − 1
else (Heap extraction)
end ← end − 1
swap(a[end], a[0])
(The following is siftDown(a, start, end))
root ← start
while iLeftChild(root) < end do
child ← iLeftChild(root)
(If there is a right child and that child is greater)
if child+1 < end and a[child] < a[child+1] then
child ← child + 1
if a[root] < a[child] then
swap(a[root], a[child])
root ← child (repeat to continue sifting down the child now)
else
break (return to outer loop)
Variations
[edit]Williams' heap construction
[edit]The description above uses Floyd's improved heap-construction algorithm, which operates in O(n) time and uses the same siftDown primitive as the heap-extraction phase. Although this algorithm, being both faster and simpler to program, is used by all practical heapsort implementations, Williams' original algorithm may be easier to understand, and is needed to implement a more general binary heap priority queue.
Rather than merging many small heaps, Williams' algorithm maintains one single heap at the front of the array and repeatedly appends an additional element using a siftUp primitive. Being at the end of the array, the new element is a leaf and has no children to worry about, but may violate the heap property by being greater than its parent. In this case, exchange it with its parent and repeat the test until the parent is greater or there is no parent (we have reached the root). In pseudocode, this is:
procedure siftUp(a, end) is
input: a is the array, which heap-ordered up to end-1.
end is the node to sift up.
while end > 0
parent := iParent(end)
if a[parent] < a[end] then (out of max-heap order)
swap(a[parent], a[end])
end := parent (continue sifting up)
else
return
procedure heapify(a, count) is
(start with a trivial single-element heap)
end := 1
while end < count
(sift up the node at index end to the proper place such that
all nodes above the end index are in heap order)
siftUp(a, end)
end := end + 1
(after sifting up the last node all nodes are in heap order)

To understand why this algorithm can take asymptotically more time to build a heap (O(n log n) vs. O(n) worst case), note that in Floyd's algorithm, almost all the calls to siftDown operations apply to very small heaps. Half the heaps are height-1 trivial heaps and can be skipped entirely, half of the remainder are height-2, and so on. Only two calls are on heaps of size n/2, and only one siftDown operation is done on the full n-element heap. The overall average siftDown operation takes O(1) time.
In contrast, Williams' algorithm most of the calls to siftUp are made on large heaps of height O(log n). Half of the calls are made with a heap size of n/2 or more, three-quarters are made with a heap size of n/4 or more, and so on. Although the average number of steps is similar to Floyd's technique, [9]: 3 pre-sorted input will cause the worst case: each added node is sifted up to the root, so the average call to siftUp will require approximately (log2n − 1)/2 + (log2n − 2)/4 + (log2n − 3)/8 + ⋯ = log2n − (1 + 1/2 + 1/4 + ⋯) = log2n − 2 iterations.
Because it is dominated by the second heap-extraction phase, the heapsort algorithm itself has O(n log n) time complexity using either version of heapify.
Bottom-up heapsort
[edit]Bottom-up heapsort is a variant which reduces the number of comparisons required by a significant factor. While ordinary "top-down" heapsort requires 2n log2 n + O(n) comparisons worst-case and on average,[10] the bottom-up variant requires n log2n + O(1) comparisons on average,[10] and 1.5n log2n + O(n) in the worst case.[11]
If comparisons are cheap (e.g. integer keys) then the difference is unimportant,[12] as top-down heapsort compares values that have already been loaded from memory. If, however, comparisons require a function call or other complex logic, then bottom-up heapsort is advantageous.
This is accomplished by using a more elaborate siftDown procedure. The change improves the linear-time heap-building phase slightly,[13] but is more significant in the second phase. Like top-down heapsort, each iteration of the second phase extracts the top of the heap, a[0], and fills the gap it leaves with a[end], then sifts this latter element down the heap. But this element came from the lowest level of the heap, meaning it is one of the smallest elements in the heap, so the sift-down will likely take many steps to move it back down.[14] In top-down heapsort, each step of siftDown requires two comparisons, to find the minimum of three elements: the new node and its two children.
Bottom-up heapsort conceptually replaces the root with a value of −∞ and sifts it down using only one comparison per level (since no child can possibly be less than −∞) until the leaves are reached, then replaces the −∞ with the correct value and sifts it up (again, using one comparison per level) until the correct position is found.
This places the root in the same location as top-down siftDown, but fewer comparisons are required to find that location. For any single siftDown operation, the bottom-up technique is advantageous if the number of downward movements is at least 2⁄3 of the height of the tree (when the number of comparisons is 4⁄3 times the height for both techniques), and it turns out that this is more than true on average, even for worst-case inputs.[11]
A naïve implementation of this conceptual algorithm would cause some redundant data copying, as the sift-up portion undoes part of the sifting down. A practical implementation searches downward for a leaf where −∞ would be placed, then upward for where the root should be placed. Finally, the upward traversal continues to the root's starting position, performing no more comparisons but exchanging nodes to complete the necessary rearrangement. This optimized form performs the same number of exchanges as top-down siftDown.
Because it goes all the way to the bottom and then comes back up, it is called heapsort with bounce by some authors.[15]
function leafSearch(a, i, end) is
j ← i
while iRightChild(j) < end do
(Determine which of j's two children is the greater)
if a[iRightChild(j)] > a[iLeftChild(j)] then
j ← iRightChild(j)
else
j ← iLeftChild(j)
(At the last level, there might be only one child)
if iLeftChild(j) < end then
j ← iLeftChild(j)
return j
The return value of the leafSearch is used in the modified siftDown routine:[11]
procedure siftDown(a, i, end) is
j ← leafSearch(a, i, end)
while a[i] > a[j] do
j ← iParent(j)
while j > i do
swap(a[i], a[j])
j ← iParent(j)
Bottom-up heapsort was announced as beating quicksort (with median-of-three pivot selection) on arrays of size ≥16000.[10]
A 2008 re-evaluation of this algorithm showed it to be no faster than top-down heapsort for integer keys, presumably because modern branch prediction nullifies the cost of the predictable comparisons which bottom-up heapsort manages to avoid.[12]
A further refinement does a binary search in the upward search, and sorts in a worst case of (n+1)(log2(n+1) + log2 log2(n+1) + 1.82) + O(log2n) comparisons, approaching the information-theoretic lower bound of n log2n − 1.4427n comparisons.[16]
A variant which uses two extra bits per internal node (n−1 bits total for an n-element heap) to cache information about which child is greater (two bits are required to store three cases: left, right, and unknown)[13] uses less than n log2n + 1.1n compares.[17]
Other variations
[edit]- Ternary heapsort uses a ternary heap instead of a binary heap; that is, each element in the heap has three children. It is more complicated to program, but does a constant number of times fewer swap and comparison operations. This is because each sift-down step in a ternary heap requires three comparisons and one swap, whereas in a binary heap two comparisons and one swap are required. Two levels in a ternary heap cover 32 = 9 elements, doing more work with the same number of comparisons as three levels in the binary heap, which only cover 23 = 8.[citation needed] This is primarily of academic interest, or as a student exercise,[18] as the additional complexity is not worth the minor savings, and bottom-up heapsort beats both.
- Memory-optimized heapsort[19]: 87 improves heapsort's locality of reference by increasing the number of children even more. This increases the number of comparisons, but because all children are stored consecutively in memory, reduces the number of cache lines accessed during heap traversal, a net performance improvement.
- The standard implementation of Floyd's heap-construction algorithm causes a large number of cache misses once the size of the data exceeds that of the CPU cache.[19]: 87 Better performance on large data sets can be obtained by merging in depth-first order, combining subheaps as soon as possible, rather than combining all subheaps on one level before proceeding to the one above.[9][20]
- Out-of-place heapsort[21][22][14] improves on bottom-up heapsort by eliminating the worst case, guaranteeing n log2n + O(n) comparisons. When the maximum is taken, rather than fill the vacated space with an unsorted data value, fill it with a −∞ sentinel value, which never "bounces" back up. It turns out that this can be used as a primitive in an in-place (and non-recursive) "QuickHeapsort" algorithm.[23] First, you perform a quicksort-like partitioning pass, but reversing the order of the partitioned data in the array. Suppose (without loss of generality) that the smaller partition is the one greater than the pivot, which should go at the end of the array, but our reversed partitioning step places it at the beginning. Form a heap out of the smaller partition and do out-of-place heapsort on it, exchanging the extracted maxima with values from the end of the array. These are less than the pivot, meaning less than any value in the heap, so serve as −∞ sentinel values. Once the heapsort is complete (and the pivot moved to just before the now-sorted end of the array), the order of the partitions has been reversed, and the larger partition at the beginning of the array may be sorted in the same way. (Because there is no non-tail recursion, this also eliminates quicksort's O(log n) stack usage.)
- The smoothsort algorithm[24] is a variation of heapsort developed by Edsger W. Dijkstra in 1981. Like heapsort, smoothsort's upper bound is O(n log n). The advantage of smoothsort is that it comes closer to O(n) time if the input is already sorted to some degree, whereas heapsort averages O(n log n) regardless of the initial sorted state. Due to its complexity, smoothsort is rarely used.[citation needed]
- Levcopoulos and Petersson[25] describe a variation of heapsort based on a heap of Cartesian trees. First, a Cartesian tree is built from the input in O(n) time, and its root is placed in a 1-element binary heap. Then we repeatedly extract the minimum from the binary heap, output the tree's root element, and add its left and right children (if any) which are themselves Cartesian trees, to the binary heap.[26] As they show, if the input is already nearly sorted, the Cartesian trees will be very unbalanced, with few nodes having left and right children, resulting in the binary heap remaining small, and allowing the algorithm to sort more quickly than O(n log n) for inputs that are already nearly sorted.
- Several variants such as weak heapsort require n log2 n+O(1) comparisons in the worst case, close to the theoretical minimum, using one extra bit of state per node. While this extra bit makes the algorithms not truly in-place, if space for it can be found inside the element, these algorithms are simple and efficient,[9]: 40 but still slower than binary heaps if key comparisons are cheap enough (e.g. integer keys) that a constant factor does not matter.[27]
- Katajainen's "ultimate heapsort" requires no extra storage, performs n log2 n+O(1) comparisons, and a similar number of element moves.[28] It is, however, even more complex and not justified unless comparisons are very expensive.
Comparison with other sorts
[edit]Heapsort primarily competes with quicksort, another very efficient general purpose in-place unstable comparison-based sort algorithm.
Heapsort's primary advantages are its simple, non-recursive code, minimal auxiliary storage requirement, and reliably good performance: its best and worst cases are within a small constant factor of each other, and of the theoretical lower bound on comparison sorts. While it cannot do better than O(n log n) for pre-sorted inputs, it does not suffer from quicksort's O(n2) worst case, either.
Real-world quicksort implementations use a variety of heuristics to avoid the worst case, but that makes their implementation far more complex, and implementations such as introsort and pattern-defeating quicksort[29] use heapsort as a last-resort fallback if they detect degenerate behaviour. Thus, their worst-case performance is slightly worse than if heapsort had been used from the beginning.
Heapsort's primary disadvantages are its poor locality of reference and its inherently serial nature; the accesses to the implicit tree are widely scattered and mostly random, and there is no straightforward way to convert it to a parallel algorithm.
The worst-case performance guarantees make heapsort popular in real-time computing, and systems concerned with maliciously chosen inputs[30] such as the Linux kernel.[31] The combination of small implementation and dependably "good enough" performance make it popular in embedded systems, and generally any application where sorting is not a performance bottleneck. E.g. heapsort is ideal for sorting a list of filenames for display, but a database management system would probably want a more aggressively optimized sorting algorithm.
A well-implemented quicksort is usually 2–3 times faster than heapsort.[19][32] Although quicksort requires fewer comparisons, this is a minor factor. (Results claiming twice as many comparisons are measuring the top-down version; see § Bottom-up heapsort.) The main advantage of quicksort is its much better locality of reference: partitioning is a linear scan with good spatial locality, and the recursive subdivision has good temporal locality. With additional effort, quicksort can also be implemented in mostly branch-free code,[33][34] and multiple CPUs can be used to sort subpartitions in parallel. Thus, quicksort is preferred when the additional performance justifies the implementation effort.
The other major O(n log n) sorting algorithm is merge sort, but that rarely competes directly with heapsort because it is not in-place. Merge sort's requirement for Ω(n) extra space (roughly half the size of the input) is usually prohibitive except in the situations where merge sort has a clear advantage:
- When a stable sort is required
- When taking advantage of (partially) pre-sorted input
- Sorting linked lists (in which case merge sort requires minimal extra space)
- Parallel sorting; merge sort parallelizes even better than quicksort and can easily achieve close to linear speedup
- External sorting; merge sort has excellent locality of reference
Example
[edit]The examples sort the values { 6, 5, 3, 1, 8, 7, 2, 4 } in increasing order using both heap-construction algorithms. The elements being compared are shown in a bold font. There are typically two when sifting up, and three when sifting down, although there may be fewer when the top or bottom of the tree is reached.
Heap construction (Williams' algorithm)
[edit]
| Heap | Unsorted | Swap elements |
|---|---|---|
| 6 | 5, 3, 1, 8, 7, 2, 4 | |
| 6, 5 | 3, 1, 8, 7, 2, 4 | |
| 6, 5, 3 | 1, 8, 7, 2, 4 | |
| 6, 5, 3, 1 | 8, 7, 2, 4 | |
| 6, 5, 3, 1, 8 | 7, 2, 4 | 5 ↔ 8 |
| 6, 8, 3, 1, 5 | 7, 2, 4 | 6 ↔ 8 |
| 8, 6, 3, 1, 5 | 7, 2, 4 | |
| 8, 6, 3, 1, 5, 7 | 2, 4 | 3 ↔ 7 |
| 8, 6, 7, 1, 5, 3 | 2, 4 | |
| 8, 6, 7, 1, 5, 3, 2 | 4 | |
| 8, 6, 7, 1, 5, 3, 2, 4 | 1 ↔ 4 | |
| 8, 6, 7, 4, 5, 3, 2, 1 |
Heap construction (Floyd's algorithm)
[edit]| Unsorted | Heap | Swap elements |
|---|---|---|
| 6, 5, 3, 1 | 8, 7, 2, 4 | |
| 6, 5, 3 | 1, 8, 7, 2, 4 | 1 ↔ 4 |
| 6, 5, 3 | 4, 8, 7, 2, 1 | |
| 6, 5 | 3, 4, 8, 7, 2, 1 | 3 ↔ 7 |
| 6, 5 | 7, 4, 8, 3, 2, 1 | |
| 6 | 5, 7, 4, 8, 3, 2, 1 | 5 ↔ 8 |
| 6 | 8, 7, 4, 5, 3, 2, 1 | |
| 6, 8, 7, 4, 5, 3, 2, 1 | 6 ↔ 8 | |
| 8, 6, 7, 4, 5, 3, 2, 1 |
Heap extraction
[edit]| Heap | Sorted array | Swap elements | Details |
|---|---|---|---|
| 8, 6, 7, 4, 5, 3, 2, 1 | 8 ↔ 1 | Add 8 to the sorted array by swapping it with 1 | |
| 1, 6, 7, 4, 5, 3, 2 | 8 | 1 ↔ 7 | Swap 1 and 7 as they are not in order in the heap |
| 7, 6, 1, 4, 5, 3, 2 | 8 | 1 ↔ 3 | Swap 1 and 3 as they are not in order in the heap |
| 7, 6, 3, 4, 5, 1, 2 | 8 | 1 has no children; siftDown complete | |
| 7, 6, 3, 4, 5, 1, 2 | 8 | 7 ↔ 2 | Add 7 to the sorted array by swapping it with 2 |
| 2, 6, 3, 4, 5, 1 | 7, 8 | 2 ↔ 6 | Swap 2 and 6 as they are not in order in the heap |
| 6, 2, 3, 4, 5, 1 | 7, 8 | 2 ↔ 5 | Swap 2 and 5 as they are not in order in the heap |
| 6, 5, 3, 4, 2, 1 | 7, 8 | 2 has no children; siftDown complete | |
| 6, 5, 3, 4, 2, 1 | 7, 8 | 6 ↔ 1 | Add 6 to the sorted array by swapping it with 1 |
| 1, 5, 3, 4, 2 | 6, 7, 8 | 1 ↔ 5 | Swap 1 and 5 as they are not in order in the heap |
| 5, 1, 3, 4, 2 | 6, 7, 8 | 1 ↔ 4 | Swap 1 and 4 as they are not in order in the heap |
| 5, 4, 3, 1, 2 | 6, 7, 8 | 1 has no children; siftDown complete | |
| 5, 4, 3, 1, 2 | 6, 7, 8 | 5 ↔ 2 | Add 5 to the sorted array by swapping it with 2 |
| 2, 4, 3, 1 | 5, 6, 7, 8 | 2 ↔ 4 | Swap 2 and 4 as they are not in order in the heap |
| 4, 2, 3, 1 | 5, 6, 7, 8 | 2 is greater than 1; siftDown complete | |
| 4, 2, 3, 1 | 5, 6, 7, 8 | Add 4 to the sorted array by swapping it with 1 | |
| 1, 2, 3 | 4, 5, 6, 7, 8 | 1 ↔ 3 | Swap 1 and 3 as they are not in order in the heap |
| 3, 2, 1 | 4, 5, 6, 7, 8 | 1 has no children; siftDown complete | |
| 3, 2, 1 | 4, 5, 6, 7, 8 | 1 ↔ 3 | Add 3 to the sorted array by swapping it with 1 |
| 1, 2 | 3, 4, 5, 6, 7, 8 | 1 ↔ 2 | Swap 1 and 2 as they are not in order in the heap |
| 2, 1 | 3, 4, 5, 6, 7, 8 | 1 has no children; siftDown complete | |
| 2, 1 | 3, 4, 5, 6, 7, 8 | 2 ↔ 1 | Add 2 to the sorted array by swapping it with 1 |
| 1 | 2, 3, 4, 5, 6, 7, 8 | Add 1 to the sorted array | |
| 1, 2, 3, 4, 5, 6, 7, 8 | Completed |
Notes
[edit]- ^ Bollobás, B.; Fenner, T. I.; Frieze, A. M. (1996). "On the Best Case of Heapsort" (PDF). Journal of Algorithms. 20 (11): 205–217. doi:10.1006/jagm.1996.0011.
- ^ Sedgewick, Robert; Schaffer, Russel W. (October 1990). The Best Case of Heapsort (Technical report). Princeton University. TR-293-90.
- ^ Skiena, Steven (2008). "Searching and Sorting". The Algorithm Design Manual (3rd ed.). Springer. p. 116. doi:10.1007/978-3-030-54256-6_4. ISBN 978-3-030-54255-9.
The name typically given to this algorithm, heapsort, obscures the fact that the algorithm is nothing but an implementation of selection sort using the right data structure.
- ^ Williams 1964
- ^ a b Brass, Peter (2008). Advanced Data Structures. Cambridge University Press. p. 209. ISBN 978-0-521-88037-4.
- ^ Suchenek, Marek A. (2012). "Elementary Yet Precise Worst-Case Analysis of Floyd's Heap-Construction Program". Fundamenta Informaticae. 120 (1): 75–92. doi:10.3233/FI-2012-751.
- ^ Suchenek, Marek A. (7 April 2015). "A Complete Worst-Case Analysis of Heapsort with Experimental Verification of Its Results, A manuscript". arXiv:1504.01459 [cs.DS].
- ^ Knuth 1997
- ^ a b c Bojesen, Jesper; Katajainen, Jyrki; Spork, Maz (2000). "Performance Engineering Case Study: Heap Construction" (PostScript). ACM Journal of Experimental Algorithmics. 5 (15): 15–es. CiteSeerX 10.1.1.35.3248. doi:10.1145/351827.384257. S2CID 30995934. Alternate PDF source.
- ^ a b c Wegener, Ingo (13 September 1993). "BOTTOM-UP HEAPSORT, a new variant of HEAPSORT beating, on an average, QUICKSORT (if n is not very small)" (PDF). Theoretical Computer Science. 118 (1): 81–98. doi:10.1016/0304-3975(93)90364-y. Although this is a reprint of work first published in 1990 (at the Mathematical Foundations of Computer Science conference), the technique was published by Carlsson in 1987.[16]
- ^ a b c Fleischer, Rudolf (February 1994). "A tight lower bound for the worst case of Bottom-Up-Heapsort" (PDF). Algorithmica. 11 (2): 104–115. doi:10.1007/bf01182770. hdl:11858/00-001M-0000-0014-7B02-C. S2CID 21075180. Also available as Fleischer, Rudolf (April 1991). A tight lower bound for the worst case of Bottom-Up-Heapsort (PDF) (Technical report). MPI-INF. MPI-I-91-104.
- ^ a b Mehlhorn, Kurt; Sanders, Peter (2008). "Priority Queues" (PDF). Algorithms and Data Structures: The Basic Toolbox. Springer. p. 142. ISBN 978-3-540-77977-3.
- ^ a b McDiarmid, C. J. H.; Reed, B. A. (September 1989). "Building heaps fast" (PDF). Journal of Algorithms. 10 (3): 352–365. doi:10.1016/0196-6774(89)90033-3.
- ^ a b MacKay, David J. C. (December 2005). "Heapsort, Quicksort, and Entropy". Retrieved 12 February 2021.
- ^ Moret, Bernard; Shapiro, Henry D. (1991). "8.6 Heapsort". Algorithms from P to NP Volume 1: Design and Efficiency. Benjamin/Cummings. p. 528. ISBN 0-8053-8008-6.
For lack of a better name we call this enhanced program 'heapsort with bounce.'
- ^ a b Carlsson, Scante (March 1987). "A variant of heapsort with almost optimal number of comparisons" (PDF). Information Processing Letters. 24 (4): 247–250. doi:10.1016/0020-0190(87)90142-6. S2CID 28135103. Archived from the original (PDF) on 27 December 2016.
- ^ Wegener, Ingo (March 1992). "The worst case complexity of McDiarmid and Reed's variant of BOTTOM-UP HEAPSORT is less than n log n + 1.1n". Information and Computation. 97 (1): 86–96. doi:10.1016/0890-5401(92)90005-Z.
- ^ Tenenbaum, Aaron M.; Augenstein, Moshe J. (1981). "Chapter 8: Sorting". Data Structures Using Pascal. Prentice-Hall. p. 405. ISBN 0-13-196501-8.
Write a sorting routine similar to the heapsort except that it uses a ternary heap.
- ^ a b c LaMarca, Anthony; Ladner, Richard E. (April 1999). "The Influence of Caches on the Performance of Sorting" (PDF). Journal of Algorithms. 31 (1): 66–104. CiteSeerX 10.1.1.456.3616. doi:10.1006/jagm.1998.0985. S2CID 206567217. See particularly figure 9c on p. 98.
- ^ Chen, Jingsen; Edelkamp, Stefan; Elmasry, Amr; Katajainen, Jyrki (27–31 August 2012). "In-place Heap Construction with Optimized Comparisons, Moves, and Cache Misses" (PDF). Mathematical Foundations of Computer Science 2012. 37th international conference on Mathematical Foundations of Computer Science. Lecture Notes in Computer Science. Vol. 7464. Bratislava, Slovakia. pp. 259–270. doi:10.1007/978-3-642-32589-2_25. ISBN 978-3-642-32588-5. S2CID 1462216. Archived from the original (PDF) on 29 December 2016. See particularly Fig. 3.
- ^ Cantone, Domenico; Concotti, Gianluca (1–3 March 2000). QuickHeapsort, an efficient mix of classical sorting algorithms. 4th Italian Conference on Algorithms and Complexity. Lecture Notes in Computer Science. Vol. 1767. Rome. pp. 150–162. ISBN 3-540-67159-5.
- ^ Cantone, Domenico; Concotti, Gianluca (August 2002). "QuickHeapsort, an efficient mix of classical sorting algorithms" (PDF). Theoretical Computer Science. 285 (1): 25–42. doi:10.1016/S0304-3975(01)00288-2. Zbl 1016.68042.
- ^ Diekert, Volker; Weiß, Armin (August 2016). "QuickHeapsort: Modifications and improved analysis". Theory of Computing Systems. 59 (2): 209–230. arXiv:1209.4214. doi:10.1007/s00224-015-9656-y. S2CID 792585.
- ^ Dijkstra, Edsger W. Smoothsort – an alternative to sorting in situ (EWD-796a) (PDF). E.W. Dijkstra Archive. Center for American History, University of Texas at Austin. (transcription)
- ^ Levcopoulos, Christos; Petersson, Ola (1989). "Heapsort—Adapted for Presorted Files". WADS '89: Proceedings of the Workshop on Algorithms and Data Structures. Lecture Notes in Computer Science. Vol. 382. London, UK: Springer-Verlag. pp. 499–509. doi:10.1007/3-540-51542-9_41. ISBN 978-3-540-51542-5. Heapsort—Adapted for presorted files (Q56049336).
- ^ Schwartz, Keith (27 December 2010). "CartesianTreeSort.hh". Archive of Interesting Code. Retrieved 5 March 2019.
- ^ Katajainen, Jyrki (23 September 2013). Seeking for the best priority queue: Lessons learnt. Algorithm Engineering (Seminar 13391). Dagstuhl. pp. 19–20, 24.
- ^ Katajainen, Jyrki (2–3 February 1998). The Ultimate Heapsort. Computing: the 4th Australasian Theory Symposium. Australian Computer Science Communications. Vol. 20, no. 3. Perth. pp. 87–96.
- ^ Peters, Orson R. L. (9 June 2021). "Pattern-defeating Quicksort". arXiv:2106.05123 [cs.DS].
Peters, Orson R. L. "pdqsort". Github. Retrieved 2 October 2023. - ^ Morris, John (1998). "Comparing Quick and Heap Sorts". Data Structures and Algorithms (Lecture notes). University of Western Australia. Retrieved 12 February 2021.
- ^ https://git.kernel.org/pub/scm/linux/kernel/git/torvalds/linux.git/tree/lib/sort.c#n205 Linux kernel source
- ^ Maus, Arne [in Norwegian] (14 May 2014). "Sorting by generating the sorting permutation, and the effect of caching on sorting". See Fig. 1 on p. 6.
- ^ Edelkamp, Stefan; Weiß, Armin (30 January 2019). "BlockQuicksort: Avoiding Branch Mispredictions in Quicksort" (PDF). Journal of Experimental Algorithmics. 24 1.4. arXiv:1604.06697. doi:10.1145/3274660.
- ^ Aumüller, Martin; Hass, Nikolaj (7–8 January 2019). Simple and Fast BlockQuicksort using Lomuto’s Partitioning Scheme. Twenty-First Workshop on Algorithm Engineering and Experiments (ALENEX). San Diego. arXiv:1810.12047. doi:10.1137/1.9781611975499.2.
References
[edit]- Williams, J. W. J. (1964). "Algorithm 232 – Heapsort". Communications of the ACM. 7 (6): 347–348. doi:10.1145/512274.512284.
- Floyd, Robert W. (1964). "Algorithm 245 – Treesort 3". Communications of the ACM. 7 (12): 701. doi:10.1145/355588.365103. S2CID 52864987.
- Carlsson, Svante [in Swedish] (1987). "Average-case results on heapsort". BIT Numerical Mathematics. 27 (1): 2–17. doi:10.1007/bf01937350. S2CID 31450060.
- Knuth, Donald (1997). "§5.2.3, Sorting by Selection". The Art of Computer Programming. Vol. 3: Sorting and Searching (3rd ed.). Addison-Wesley. pp. 144–155. ISBN 978-0-201-89685-5.
- Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001). Introduction to Algorithms (2nd ed.). MIT Press and McGraw-Hill. ISBN 0-262-03293-7. Chapters 6 and 7 Respectively: Heapsort and Priority Queues
- A PDF of Dijkstra's original paper on Smoothsort
- Heaps and Heapsort Tutorial by David Carlson, St. Vincent College
External links
[edit]- Animated Sorting Algorithms: Heap Sort at the Wayback Machine (archived 6 March 2015) – graphical demonstration
- Courseware on Heapsort from Univ. Oldenburg – With text, animations and interactive exercises
- NIST's Dictionary of Algorithms and Data Structures: Heapsort
- Heapsort implemented in 12 languages Archived 28 December 2010 at the Wayback Machine
- Sorting revisited by Paul Hsieh
- A PowerPoint presentation demonstrating how Heap sort works that is for educators.
- Open Data Structures – Section 11.1.3 – Heap-Sort, Pat Morin



