Isohedron
Appearance
In geometry, an isohedron is a polyhedron with symmetries acting transitively on its faces. Their topology can be represented by a face configuration. All 5 Platonic solids and 13 Catalan solids are isohedra, as well as the infinite families of trapezohedra and bipyramids. Some forms allow geometric variations including concave and self-intersecting geometries
Convex isohedra make fair dice. An isohedron has an even number of faces.[1]
Examples
| Faces | Face config. |
Class | Name | Symmetry | Image variations |
|---|---|---|---|---|---|
| 4 | V33 | Platonic | tetrahedron tetragonal disphenoid rhombic disphenoid |
Td, [3,3], (*332) D2d, [2+,2], (2*) D2, [2,2]+, (222) |
 
|
| 6 | V34 | Platonic | cube trigonal trapezohedron asymmetric trigonal trapezohedron |
Oh, [4,3], (*432) D3d, [2+,6], (2*3) D3, [2,3]+, (223) |
 
|
| 8 | V43 | Platonic | octahedron square bipyramid rhombic bipyramid square scalenohedron |
Oh, [4,3], (*432) D4h, [2,4], (*224) D2h, [2,2], (*222) D2d, [2+,4], (2*2) |
 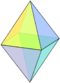    
|
| 12 | V53 | Platonic | dodecahedron pyritohedron tetartoid |
Ih, [5,3], (*532) Th, [3+,4], (3*2) T, [3,3]+, (*332) |
 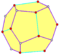 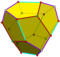 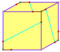 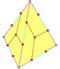  
|
| 20 | V35 | Platonic | icosahedron | Ih, [5,3], (*532) | 
|
| 12 | V3.62 | Catalan | triakis tetrahedron | Td, [3,3], (*332) |    
|
| 12 | V(3.4)2 | Catalan | rhombic dodecahedron trapezoidal dodedecahedron |
Oh, [4,3], (*432) Td, [3,3], (*332) |
     
|
| 24 | V3.82 | Catalan | triakis octahedron | Oh, [4,3], (*432) |   
|
| 24 | V4.62 | Catalan | tetrakis hexahedron | Oh, [4,3], (*432) |      
|
| 24 | V3.43 | Catalan | deltoidal icositetrahedron | Oh, [4,3], (*432) |  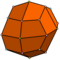    
|
| 48 | V4.6.8 | Catalan | disdyakis dodecahedron | Oh, [4,3], (*432) |      
|
| 24 | V34.4 | Catalan | pentagonal icositetrahedron | O, [4,3]+, (432) | 
|
| 30 | V(3.5)2 | Catalan | rhombic triacontahedron | Ih, [5,3], (*532) |  
|
| 60 | V3.102 | Catalan | triakis icosahedron | Ih, [5,3], (*532) |     
|
| 60 | V5.62 | Catalan | pentakis dodecahedron | Ih, [5,3], (*532) |      
|
| 60 | V3.4.5.4 | Catalan | deltoidal hexecontahedron | Ih, [5,3], (*532) | 
|
| 120 | V4.6.10 | Catalan | disdyakis triacontahedron | Ih, [5,3], (*532) |       
|
| 60 | V34.5 | Catalan | pentagonal hexecontahedron | I, [5,3]+, (532) | 
|
| 2n | V33.n | Polar | trapezohedron asymmetric trapezohedron |
Dnd, [2+,2n], (2*n) Dn, [2,n]+, (22n) |
 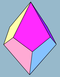 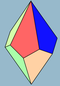 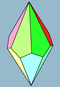
|
| 2n 4n |
V42.n V42.2n V42.2n |
Polar | regular n-bipyramid isotoxal 2n-bipyramid 2n-scalenohedron |
Dnh, [2,n], (*22n) Dnh, [2,n], (*22n) Dnd, [2+,2n], (2*n) |
 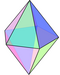     
|
References
- ^ Grünbaum (1960)
- Weisstein, Eric W. "Isohedron". MathWorld.
- Branko Grünbaum On Polyhedra in E3 having all faces congruent. Bull. Research Council Israel 8F, 215-218, 1960.
External links
- isohedra 25 classes of isohedra with a finite number of sides
