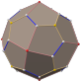
Triakis octahedron

Triakis octahedron
(Click here for rotating model)
Type	Catalan solid
Coxeter diagram
Face type	isosceles triangle
Faces	24
Edges	36
Vertices	14
Vertices by type	8{3}+6{8}
Face configuration	V3.8.8
Symmetry group	Oh, BC3, [4,3], *432
Rotation group	O, [4,3]+, 432
Dihedral angle	147° 21' 0" $\arccos ( -\frac{3 + 8\sqrt{2}}{17} )$
Properties	convex, face-transitive
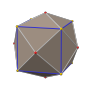
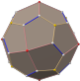
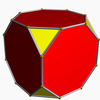Truncated cube (dual polyhedron)	Net

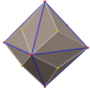
In geometry, a triakis octahedron is an Archimedean dual solid, or a Catalan solid. Its dual is the truncated cube.

It can be seen as an octahedron with triangular pyramids added to each face; that is, it is the Kleetope of the octahedron. It is also sometimes called a trisoctahedron, or, more fully, trigonal trisoctahedron. Both names reflect the fact that it has three triangular faces for every face of an octahedron. The tetragonal trisoctahedron is another name for the deltoidal icositetrahedron, a different polyhedron with three quadrilateral faces for every face of an octahedron.

This convex polyhedron is topologically similar to the concave stellated octahedron. They have the same face connectivity, but the vertices are in different relative distances from the center.

It is also called the small triakis octahedron, so as to differentiate it from the great triakis octahedron, the dual of the stellated truncated hexahedron.

If its shorter edges have length 1, its surface area and volume are:

$A=3\sqrt{7+4\sqrt{2}}$

$V=\frac{1}{2}(3+2\sqrt{2}).$

Cultural references

• A triakis octahedron is a vital element in the plot of cult author Hugh Cook's novel The Wishstone and the Wonderworkers.

Related polyhedra

The triakis octahedron is one of a family of duals to the uniform polyhedra related to the cube and regular octahedron.

Uniform octahedral polyhedra

Symmetry: [4,3], (*432)							[4,3]+, (432)	[1+,4,3], (*332)	[4,3+], (3*2)
{4,3}	t0,1{4,3}	t1{4,3}	t1,2{4,3}	{3,4}	t0,2{4,3}	t0,1,2{4,3}	s{4,3}	h{4,3}	h1,2{4,3}
Duals to uniform polyhedra
V4.4.4	V3.8.8	V3.4.3.4	V4.6.6	V3.3.3.3	V3.4.4.4	V4.6.8	V3.3.3.3.4	V3.3.3	V3.3.3.3.3

The triakis octahedron is a part of a sequence of polyhedra and tilings, extending into the hyperbolic plane. These face-transitive figures have (*n32) reflectional symmetry.

Dimensional family of truncated polyhedra and tilings: 3.2n.2n

Symmetry *n32 [n,3]	Spherical				Euclidean	Hyperbolic...
	*232 [2,3] D3h	*332 [3,3] Td	*432 [4,3] Oh	*532 [5,3] Ih	*632 [6,3] P6m	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]
Truncated figures	3.4.4	3.6.6	3.8.8	3.10.10	3.12.12	3.14.14	3.16.16	3.∞.∞
Coxeter Schläfli	t0,1{2,3}	t0,1{3,3}	t0,1{4,3}	t0,1{5,3}	t0,1{6,3}	t0,1{7,3}	t0,1{8,3}	t0,1{∞,3}
Uniform dual figures
Triakis figures	V3.4.4	V3.6.6	V3.8.8	V3.10.10	V3.12.12	V3.14.14	V3.16.16	V3.∞.∞
Coxeter

The triakis octahedron is also a part of a sequence of polyhedra and tilings, extending into the hyperbolic plane. These face-transitive figures have (*n42) reflectional symmetry.

Dimensional family of truncated polyhedra and tilings: n.8.8

Symmetry *n42 [n,4]	Spherical		Euclidean	Hyperbolic...
	*242 [2,4] D4h	*342 [3,4] Oh	*442 [4,4] P4m	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]...	*∞42 [∞,4]
Truncated figures	2.8.8	3.8.8	4.8.8	5.8.8	6.8.8	7.8.8	8.8.8	∞.8.8
Coxeter Schläfli	t0,1{4,2}	t0,1{4,3}	t0,1{4,4}	t0,1{4,5}	t0,1{4,6}	t0,1{4,7}	t0,1{4,8}	t0,1{4,∞}
Uniform dual figures
n-kis figures	V2.8.8	V3.8.8	V4.8.8	V5.8.8	V6.8.8	V7.8.8	V8.8.8	V∞.8.8
Coxeter

References

• Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X.  (Section 3-9)
• Wenninger, Magnus (1983), Dual Models, Cambridge University Press, ISBN 978-0-521-54325-5, MR730208  (The thirteen semiregular convex polyhedra and their duals, Page 17, Triakisoctahedron)
• The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5 [1] (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, page 284, Triakis octahedron)

External links

• Eric W. Weisstein, Triakis octahedron (Catalan solid) at MathWorld
• Triakis Octahedron – Interactive Polyhedron Model
• Virtual Reality Polyhedra www.georgehart.com: The Encyclopedia of Polyhedra
  • VRML model
  • Conway Notation for Polyhedra Try: "dtC"