List of fractals by Hausdorff dimension
According to Benoit Mandelbrot, "A fractal is by definition a set for which the Hausdorff-Besicovitch dimension strictly exceeds the topological dimension."[1] Presented here is a list of fractals, ordered by increasing Hausdorff dimension, to illustrate what it means for a fractal to have a low or a high dimension.
Deterministic fractals[edit]
| Hausdorff dimension (exact value) |
Hausdorff dimension (approx.) |
Name | Illustration | Remarks |
|---|---|---|---|---|
| Calculated | 0.538 | Feigenbaum attractor | 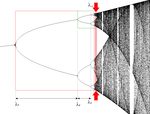 |
The Feigenbaum attractor (see between arrows) is the set of points generated by successive iterations of the logistic function for the critical parameter value , where the period doubling is infinite. This dimension is the same for any differentiable and unimodal function.[2] |
| 0.6309 | Cantor set | Built by removing the central third at each iteration. Nowhere dense and not a countable set. | ||
| 0<D<1 | 1D generalized symmetric Cantor set |  |
Built by removing the central interval of length from each remaining interval of length at the nth iteration. produces the usual middle-third Cantor set. Varying between 0 and 1 yields any fractal dimension .[3] | |
| 0.6942 | (1/4, 1/2) asymmetric Cantor set |  |
Built by removing the second quarter at each iteration.[4]
(golden ratio). | |
| 0.69897 | Real numbers whose base 10 digits are even |  |
Similar to the Cantor set.[5] | |
| 0.88137 | Spectrum of Fibonacci Hamiltonian | The study of the spectrum of the Fibonacci Hamiltonian proves upper and lower bounds for its fractal dimension in the large coupling regime. These bounds show that the spectrum converges to an explicit constant.[6][page needed] | ||
| 1 | Smith–Volterra–Cantor set | Built by removing the central interval of length from each remaining interval at the nth iteration. Nowhere dense but has a Lebesgue measure of 1/2. | ||
| 1 | Takagi or Blancmange curve |  |
Defined on the unit interval by , where is the triangle wave function. Not a fractal under Mandelbrot's definition, because its topological dimension is also .[7] Special case of the Takahi-Landsberg curve: with . The Hausdorff dimension equals for in . (Hunt cited by Mandelbrot[8]). | |
| Calculated | 1.0812 | Julia set z² + 1/4 | 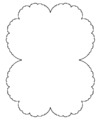 |
Julia set of f(z) = z2 + 1/4.[9] |
| Solution s of | 1.0933 | Boundary of the Rauzy fractal |  |
Fractal representation introduced by G.Rauzy of the dynamics associated to the Tribonacci morphism: , and .[10][page needed][11] is one of the conjugated roots of . |
| 1.12915 | contour of the Gosper island |  |
Term used by Mandelbrot (1977).[12] The Gosper island is the limit of the Gosper curve. | |
| Measured (box counting) | 1.2 | Dendrite Julia set |  |
Julia set of f(z) = z2 + i. |
| 1.2083 | Fibonacci word fractal 60° |  |
Build from the Fibonacci word. See also the standard Fibonacci word fractal.
(golden ratio). | |
| 1.2108 | Boundary of the tame twindragon |  |
One of the six 2-rep-tiles in the plane (can be tiled by two copies of itself, of equal size).[13][14] | |
| 1.26 | Hénon map |  |
The canonical Hénon map (with parameters a = 1.4 and b = 0.3) has Hausdorff dimension 1.261 ± 0.003. Different parameters yield different dimension values. | |
| 1.2619 | Triflake |  |
Three anti-snowflakes arranged in a way that a koch-snowflake forms in between the anti-snowflakes. | |
| 1.2619 | Koch curve |  |
3 Koch curves form the Koch snowflake or the anti-snowflake. | |
| 1.2619 | boundary of Terdragon curve |  |
L-system: same as dragon curve with angle = 30°. The Fudgeflake is based on 3 initial segments placed in a triangle. | |
| 1.2619 | 2D Cantor dust |  |
Cantor set in 2 dimensions. | |
| 1.2619 | 2D L-system branch |  |
L-Systems branching pattern having 4 new pieces scaled by 1/3. Generating the pattern using statistical instead of exact self-similarity yields the same fractal dimension. | |
| Calculated | 1.2683 | Julia set z2 − 1 |  |
Julia set of f(z) = z2 - 1.[9] |
| 1.3057 | Apollonian gasket |  |
Starting with 3 tangent circles, repeatedly packing new circles into the complementary interstices. Also the limit set generated by reflections in 4 mutually tangent circles. See[9] | |
| 1.328 | 5 circles inversion fractal |  |
The limit set generated by iterated inversions with respect to 5 mutually tangent circles (in red). Also an Apollonian packing. See[15] | |
| 1.36521[16] | Quadratic von Koch island using the type 1 curve as generator |  |
Also known as the Minkowski Sausage | |
| Calculated | 1.3934 | Douady rabbit | 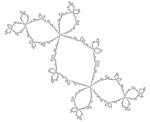 |
Julia set of f(z) = -0.123 + 0.745i[9] |
| 1.4649 | Vicsek fractal |  |
Built by exchanging iteratively each square by a cross of 5 squares. | |
| 1.4649 | Quadratic von Koch curve (type 1) |  |
One can recognize the pattern of the Vicsek fractal (above). | |
| 1.4961 | Quadric cross |  |
 Images generated with Fractal Generator for ImageJ. | |
| 1.5000 | a Weierstrass function: |  |
The Hausdorff dimension of the graph of the Weierstrass function defined by with and is .[17][18] | |
| 1.5000 | Quadratic von Koch curve (type 2) |  |
Also called "Minkowski sausage". | |
| 1.5236 | Boundary of the Dragon curve |  |
cf. Chang & Zhang.[19][14] | |
| 1.5236 | Boundary of the twindragon curve |  |
Can be built with two dragon curves. One of the six 2-rep-tiles in the plane (can be tiled by two copies of itself, of equal size).[13] | |
| 1.5850 | 3-branches tree |  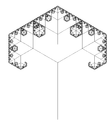 |
Each branch carries 3 branches (here 90° and 60°). The fractal dimension of the entire tree is the fractal dimension of the terminal branches. NB: the 2-branches tree has a fractal dimension of only 1. | |
| 1.5850 | Sierpinski triangle |  |
Also the limiting shape of Pascal's triangle modulo 2. | |
| 1.5850 | Sierpiński arrowhead curve |  |
Same limit as the triangle (above) but built with a one-dimensional curve. | |
| 1.5850 | Boundary of the T-square fractal | The dimension of the fractal itself (not the boundary) is | ||
| 1.61803 | a golden dragon |  |
Built from two similarities of ratios and , with . Its dimension equals because .
(golden ratio). | |
| 1.6309 | Pascal triangle modulo 3 |  |
For a triangle modulo k, if k is prime, the fractal dimension is (cf. Stephen Wolfram[20]). | |
| 1.6309 | Sierpinski Hexagon |  |
Built in the manner of the Sierpinski carpet, on an hexagonal grid, with 6 similitudes of ratio 1/3. The Koch snowflake is present at all scales. | |
| 1.6379 | Fibonacci word fractal | 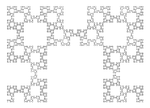 |
Fractal based on the Fibonacci word (or Rabbit sequence) Sloane A005614. Illustration : Fractal curve after 23 steps (F23 = 28657 segments).[21]
(golden ratio). | |
| Solution of | 1.6402 | Attractor of IFS with 3 similarities of ratios 1/3, 1/2 and 2/3 |  |
Generalization : Providing the open set condition holds, the attractor of an iterated function system consisting of similarities of ratios , has Hausdorff dimension , solution of the equation coinciding with the iteration function of the Euclidean contraction factor: .[5] |
| 1.6667 | 32-segment quadric fractal (1/8 scaling rule) |  see also: File:32 Segment One Eighth Scale Quadric Fractal.jpg see also: File:32 Segment One Eighth Scale Quadric Fractal.jpg
|
 | |
| 1.6826 | Pascal triangle modulo 5 |  |
For a triangle modulo k, if k is prime, the fractal dimension is (cf. Stephen Wolfram[20]). | |
| Measured (box-counting) | 1.7 | Ikeda map attractor |  |
For parameters a=1, b=0.9, k=0.4 and p=6 in the Ikeda map . It derives from a model of the plane-wave interactivity field in an optical ring laser. Different parameters yield different values.[22] |
| 1.6990 | 50 segment quadric fractal (1/10 scaling rule) |  |
Built by scaling the 50 segment generator (see inset) by 1/10 for each iteration, and replacing each segment of the previous structure with a scaled copy of the entire generator. The structure shown is made of 4 generator units and is iterated 3 times. The fractal dimension for the theoretical structure is log 50/log 10 = 1.6990. Images generated with Fractal Generator for ImageJ[23]. | |
| 1.7227 | Pinwheel fractal | 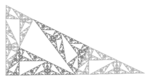 |
Built with Conway's Pinwheel tile. | |
| 1.7712 | Sphinx fractal |  |
Built with the Sphinx hexiamond tiling, removing two of the nine sub-sphinxes.[24] | |
| 1.7712 | Hexaflake |  |
Built by exchanging iteratively each hexagon by a flake of 7 hexagons. Its boundary is the von Koch flake and contains an infinity of Koch snowflakes (black or white). | |
| 1.7712 | Fractal H-I de Rivera | 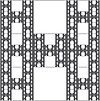 |
Starting from a unit square dividing its dimensions into three equal parts to form nine self-similar squares with the first square, two middle squares (the one that is above and the one below the central square) are removed in each of the seven squares not eliminated the process is repeated, so it continues indefinitely. | |
| 1.7848 | Von Koch curve 85° |  |
Generalizing the von Koch curve with an angle a chosen between 0 and 90°. The fractal dimension is then . | |
| 1.8272 | A self-affine fractal set |  |
Build iteratively from a array on a square, with . Its Hausdorff dimension equals [5] with and is the number of elements in the th column. The box-counting dimension yields a different formula, therefore, a different value. Unlike self-similar sets, the Hausdorff dimension of self-affine sets depends on the position of the iterated elements and there is no formula, so far, for the general case. | |
| 1.8617 | Pentaflake |  |
Built by exchanging iteratively each pentagon by a flake of 6 pentagons.
(golden ratio). | |
| solution of | 1.8687 | Monkeys tree |  |
This curve appeared in Benoit Mandelbrot's "Fractal geometry of Nature" (1983). It is based on 6 similarities of ratio and 5 similarities of ratio .[25] |
| 1.8928 | Sierpinski carpet |  |
Each face of the Menger sponge is a Sierpinski carpet, as is the bottom surface of the 3D quadratic Koch surface (type 1). | |
| 1.8928 | 3D Cantor dust |  |
Cantor set in 3 dimensions. | |
| 1.8928 | Cartesian product of the von Koch curve and the Cantor set | 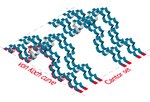 |
Generalization : Let F×G be the cartesian product of two fractals sets F and G. Then .[5] See also the 2D Cantor dust and the Cantor cube. | |
| where | 1.9340 | Boundary of the Lévy C curve |  |
Estimated by Duvall and Keesling (1999). The curve itself has a fractal dimension of 2. |
| 2 | Penrose tiling | 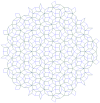 |
See Ramachandrarao, Sinha & Sanyal.[26] | |
| 2 | Boundary of the Mandelbrot set |  |
The boundary and the set itself have the same Hausdorff dimension.[27] | |
| 2 | Julia set |  |
For determined values of c (including c belonging to the boundary of the Mandelbrot set), the Julia set has a dimension of 2.[27] | |
| 2 | Sierpiński curve |  |
Every space-filling curve filling the plane has a Hausdorff dimension of 2. | |
| 2 | Hilbert curve |  |
||
| 2 | Peano curve |  |
And a family of curves built in a similar way, such as the Wunderlich curves. | |
| 2 | Moore curve |  |
Can be extended in 3 dimensions. | |
| 2 | Lebesgue curve or z-order curve |  |
Unlike the previous ones this space-filling curve is differentiable almost everywhere. Another type can be defined in 2D. Like the Hilbert Curve it can be extended in 3D.[28] | |
| 2 | Dragon curve |  |
And its boundary has a fractal dimension of 1.5236270862.[29] | |
| 2 | Terdragon curve |  |
L-system: F → F + F – F, angle = 120°. | |
| 2 | Gosper curve |  |
Its boundary is the Gosper island. | |
| Solution of | 2 | Curve filling the Koch snowflake |  |
Proposed by Mandelbrot in 1982,[30] it fills the Koch snowflake. It is based on 7 similarities of ratio 1/3 and 6 similarities of ratio . |
| 2 | Sierpiński tetrahedron |  |
Each tetrahedron is replaced by 4 tetrahedra. | |
| 2 | H-fractal |  |
Also the Mandelbrot tree which has a similar pattern. | |
| 2 | Pythagoras tree (fractal) |  |
Every square generates two squares with a reduction ratio of . | |
| 2 | 2D Greek cross fractal |  |
Each segment is replaced by a cross formed by 4 segments. | |
| Measured | 2.01 ±0.01 | Rössler attractor |  |
The fractal dimension of the Rössler attractor is slightly above 2. For a=0.1, b=0.1 and c=14 it has been estimated between 2.01 and 2.02.[31] |
| Measured | 2.06 ±0.01 | Lorenz attractor |  |
For parameters ,=16 and . See McGuinness (1983)[32] |
| 2<D<2.3 | Pyramid surface |  |
Each triangle is replaced by 6 triangles, of which 4 identical triangles form a diamond based pyramid and the remaining two remain flat with lengths and relative to the pyramid triangles. The dimension is a parameter, self-intersection occurs for values greater than 2.3.[33] | |
| 2.3219 | Fractal pyramid |  |
Each square pyramid is replaced by 5 half-size square pyramids. (Different from the Sierpinski tetrahedron, which replaces each triangular pyramid with 4 half-size triangular pyramids). | |
| 2.3296 | Dodecahedron fractal |  |
Each dodecahedron is replaced by 20 dodecahedra.
(golden ratio). | |
| 2.3347 | 3D quadratic Koch surface (type 1) |  |
Extension in 3D of the quadratic Koch curve (type 1). The illustration shows the first (blue block), second (plus green blocks), third (plus yellow blocks) and fourth (plus clear blocks) iterations. | |
| 2.4739 | Apollonian sphere packing |  |
The interstice left by the Apollonian spheres. Apollonian gasket in 3D. Dimension calculated by M. Borkovec, W. De Paris, and R. Peikert.[34] | |
| 2.50 | 3D quadratic Koch surface (type 2) | 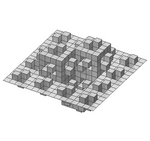 |
Extension in 3D of the quadratic Koch curve (type 2). The illustration shows the second iteration. | |
| 2.529 | Jerusalem cube |  |
The iteration n is built with 8 cubes of iteration n-1 (at the corners) and 12 cubes of iteration n-2 (linking the corners). The contraction ratio is . | |
| 2.5819 | Icosahedron fractal |  |
Each icosahedron is replaced by 12 icosahedra.
(golden ratio). | |
| 2.5849 | 3D Greek cross fractal |  |
Each segment is replaced by a cross formed by 6 segments. | |
| 2.5849 | Octahedron fractal |  |
Each octahedron is replaced by 6 octahedra. | |
| 2.5849 | von Koch surface | 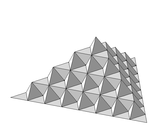 |
Each equilateral triangular face is cut into 4 equal triangles.
Using the central triangle as the base, form a tetrahedron. Replace the triangular base with the tetrahedral "tent". | |
| 2.7095 | Von Koch in 3D |  |
Start with a 6-sided polyhedron whose faces are isosceles triangles with sides of ratio 2:2:3 . Replace each polyhedron with 3 copies of itself, 2/3 smaller.[35] | |
| 2.7268 | Menger sponge |  |
And its surface has a fractal dimension of , which is the same as that by volume. | |
| 3 | 3D Hilbert curve |  |
A Hilbert curve extended to 3 dimensions. | |
| 3 | 3D Lebesgue curve |  |
A Lebesgue curve extended to 3 dimensions. | |
| 3 | 3D Moore curve |  |
A Moore curve extended to 3 dimensions. | |
| 3 | 3D H-fractal |  |
A H-fractal extended to 3 dimensions.[36] | |
| (conjectured) | 3 (to be confirmed) | Mandelbulb |  |
Extension of the Mandelbrot set (power 9) in 3 dimensions[37][unreliable source?] |
Random and natural fractals[edit]
| Hausdorff dimension (exact value) |
Hausdorff dimension (approx.) |
Name | Illustration | Remarks |
|---|---|---|---|---|
| 1/2 | 0.5 | Zeros of a Wiener process |  |
The zeros of a Wiener process (Brownian motion) are a nowhere dense set of Lebesgue measure 0 with a fractal structure.[5][38] |
| Solution of where and | 0.7499 | a random Cantor set with 50% - 30% |  |
Generalization: at each iteration, the length of the left interval is defined with a random variable , a variable percentage of the length of the original interval. Same for the right interval, with a random variable . Its Hausdorff Dimension satisfies: (where is the expected value of ).[5] |
| Solution of | 1.144... | von Koch curve with random interval | The length of the middle interval is a random variable with uniform distribution on the interval (0,1/3).[5] | |
| Measured | 1.22±0.02 | Coastline of Ireland |  |
Values for the fractal dimension of the entire coast of Ireland were determined by McCartney, Abernethy and Gault[39] at the University of Ulster and Theoretical Physics students at Trinity College, Dublin, under the supervision of S. Hutzler.[40]
Note that there are marked differences between Ireland's ragged west coast (fractal dimension of about 1.26) and the much smoother east coast (fractal dimension 1.10)[40] |
| Measured | 1.25 | Coastline of Great Britain | 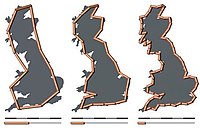 |
Fractal dimension of the west coast of Great Britain, as measured by Lewis Fry Richardson and cited by Benoît Mandelbrot.[41] |
| 1.2619 | von Koch curve with random orientation | 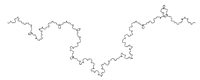 |
One introduces here an element of randomness which does not affect the dimension, by choosing, at each iteration, to place the equilateral triangle above or below the curve.[5] | |
| 1.333 | Boundary of Brownian motion | 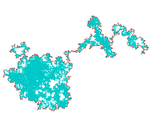 |
(cf. Mandelbrot, Lawler, Schramm, Werner).[42] | |
| 1.333 | Polymer in 2D | Similar to the Brownian motion in 2D with non-self-intersection.[43] | ||
| 1.333 | Percolation front in 2D, Corrosion front in 2D |  |
Fractal dimension of the percolation-by-invasion front (accessible perimeter), at the percolation threshold (59.3%). It's also the fractal dimension of a stopped corrosion front.[43] | |
| 1.40 | Clusters of clusters 2D | When limited by diffusion, clusters combine progressively to a unique cluster of dimension 1.4.[43] | ||
| 1.5 | Graph of a regular Brownian function (Wiener process) | 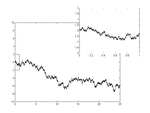 |
Graph of a function such that, for any two positive reals and , the difference of their images has the centered gaussian distribution with variance . Generalization: the fractional Brownian motion of index follows the same definition but with a variance , in that case its Hausdorff dimension .[5] | |
| Measured | 1.52 | Coastline of Norway |  |
See J. Feder.[44] |
| Measured | 1.55 | Self-avoiding walk |  |
Random walk in a square lattice that avoids visiting the same place twice, with a "go-back" routine for avoiding dead ends. |
| 1.66 | Polymer in 3D | Similar to the Brownian motion in a cubic lattice, but without self-intersection.[43] | ||
| 1.70 | 2D DLA Cluster |  |
In 2 dimensions, clusters formed by diffusion-limited aggregation, have a fractal dimension of around 1.70.[43] | |
| 1.7381 | Fractal percolation with 75% probability |  |
The fractal percolation model is constructed by the progressive replacement of each square by a grid in which is placed a random collection of sub-squares, each sub-square being retained with probability p. The "almost sure" Hausdorff dimension equals .[5] | |
| 7/4 | 1.75 | 2D percolation cluster hull |  |
The hull or boundary of a percolation cluster. Can also be generated by a hull-generating walk,[45] or by Schramm-Loewner Evolution. |
| 1.8958 | 2D percolation cluster |  |
In a square lattice, under the site percolation threshold (59.3%) the percolation-by-invasion cluster has a fractal dimension of 91/48.[43][46] Beyond that threshold, the cluster is infinite and 91/48 becomes the fractal dimension of the "clearings". | |
| 2 | Brownian motion |  |
Or random walk. The Hausdorff dimensions equals 2 in 2D, in 3D and in all greater dimensions (K.Falconer "The geometry of fractal sets"). | |
| Measured | Around 2 | Distribution of galaxy clusters |  |
From the 2005 results of the Sloan Digital Sky Survey.[47] |
| 2.5 | Balls of crumpled paper |  |
When crumpling sheets of different sizes but made of the same type of paper and with the same aspect ratio (for example, different sizes in the ISO 216 A series), then the diameter of the balls so obtained elevated to a non-integer exponent between 2 and 3 will be approximately proportional to the area of the sheets from which the balls have been made.[48] Creases will form at all size scales (see Universality (dynamical systems)). | |
| 2.50 | 3D DLA Cluster |  |
In 3 dimensions, clusters formed by diffusion-limited aggregation, have a fractal dimension of around 2.50.[43] | |
| 2.50 | Lichtenberg figure |  |
Their appearance and growth appear to be related to the process of diffusion-limited aggregation or DLA.[43] | |
| 2.5 | regular Brownian surface |  |
A function , gives the height of a point such that, for two given positive increments and , then has a centered Gaussian distribution with variance = . Generalization: the fractional Brownian surface of index follows the same definition but with a variance , in that case its Hausdorff dimension .[5] | |
| Measured | 2.52 | 3D percolation cluster |  |
In a cubic lattice, at the site percolation threshold (31.1%), the 3D percolation-by-invasion cluster has a fractal dimension of around 2.52.[46] Beyond that threshold, the cluster is infinite. |
| Measured and calculated | ~2.7 | The surface of Broccoli |  |
San-Hoon Kim used a direct scanning method and a cross section analysis of a broccoli to conclude that the fractal dimension of it is ~2.7.[49] |
| Measured | ~2.8 | Surface of human brain |  |
Measured with segmented three-dimensional high-resolution magnetic resonance images[50] |
| Measured and calculated | ~2.8 | Cauliflower |  |
San-Hoon Kim used a direct scanning method and a mathematical analysis of the cross section of a cauliflower to conclude that the fractal dimension of it is ~2.8.[49] |
| 2.97 | Lung surface | 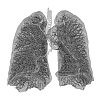 |
The alveoli of a lung form a fractal surface close to 3.[43] | |
| Calculated | Multiplicative cascade |  |
This is an example of a multifractal distribution. However, by choosing its parameters in a particular way we can force the distribution to become a monofractal.[51] |
See also[edit]
Notes and references[edit]
- ^ Mandelbrot 1982, p. 15
- ^ Aurell, Erik (May 1987). "On the metric properties of the Feigenbaum attractor". Journal of Statistical Physics. 47 (3–4): 439–458. Bibcode:1987JSP....47..439A. doi:10.1007/BF01007519. S2CID 122213380.
- ^ Cherny, A. Yu; Anitas, E.M.; Kuklin, A.I.; Balasoiu, M.; Osipov, V.A. (2010). "The scattering from generalized Cantor fractals". J. Appl. Crystallogr. 43 (4): 790–7. arXiv:0911.2497. doi:10.1107/S0021889810014184. S2CID 94779870.
- ^ Tsang, K. Y. (1986). "Dimensionality of Strange Attractors Determined Analytically". Phys. Rev. Lett. 57 (12): 1390–1393. Bibcode:1986PhRvL..57.1390T. doi:10.1103/PhysRevLett.57.1390. PMID 10033437.
- ^ a b c d e f g h i j k Falconer, Kenneth (1990–2003). Fractal Geometry: Mathematical Foundations and Applications. John Wiley & Sons, Ltd. xxv. ISBN 978-0-470-84862-3.
- ^ Damanik, D.; Embree, M.; Gorodetski, A.; Tcheremchantse, S. (2008). "The Fractal Dimension of the Spectrum of the Fibonacci Hamiltonian". Commun. Math. Phys. 280 (2): 499–516. arXiv:0705.0338. Bibcode:2008CMaPh.280..499D. doi:10.1007/s00220-008-0451-3. S2CID 12245755.
- ^ Vaz, Cristina (2019). Noções Elementares Sobre Dimensão. ISBN 9788565054867.
- ^ Mandelbrot, Benoit (2002). Gaussian self-affinity and Fractals. Springer. ISBN 978-0-387-98993-8.
- ^ a b c d McMullen, Curtis T. (3 October 1997). "Hausdorff dimension and conformal dynamics III: Computation of dimension", Abel.Math.Harvard.edu. Accessed: 27 October 2018.
- ^ Messaoudi, Ali. Frontième de numération complexe", matwbn.icm.edu.pl. (in French) Accessed: 27 October 2018.
- ^ Lothaire, M. (2005), Applied combinatorics on words, Encyclopedia of Mathematics and its Applications, vol. 105, Cambridge University Press, p. 525, ISBN 978-0-521-84802-2, MR 2165687, Zbl 1133.68067
- ^ Weisstein, Eric W. "Gosper Island". MathWorld. Retrieved 27 October 2018.
- ^ a b Ngai, Sirvent, Veerman, and Wang (October 2000). "On 2-Reptiles in the Plane 1999", Geometriae Dedicata, Volume 82. Accessed: 29 October 2018.
- ^ a b Duda, Jarek (March 2011). "The Boundary of Periodic Iterated Function Systems", Wolfram.com.
- ^ Chang, Angel and Zhang, Tianrong. "On the Fractal Structure of the Boundary of Dragon Curve". Archived from the original on 14 June 2011. Retrieved 9 February 2019.
{{cite web}}: CS1 maint: bot: original URL status unknown (link) pdf - ^ Mandelbrot, B. B. (1983). The Fractal Geometry of Nature, p.48. New York: W. H. Freeman. ISBN 9780716711865. Cited in: Weisstein, Eric W. "Minkowski Sausage". MathWorld. Retrieved 22 September 2019.
- ^ Shen, Weixiao (2018). "Hausdorff dimension of the graphs of the classical Weierstrass functions". Mathematische Zeitschrift. 289 (1–2): 223–266. arXiv:1505.03986. doi:10.1007/s00209-017-1949-1. ISSN 0025-5874. S2CID 118844077.
- ^ N. Zhang. The Hausdorff dimension of the graphs of fractal functions. (In Chinese). Master Thesis. Zhejiang University, 2018.
- ^ Fractal dimension of the boundary of the dragon fractal
- ^ a b "Fractal dimension of the Pascal triangle modulo k". Archived from the original on 15 October 2012. Retrieved 2 October 2006.
- ^ The Fibonacci word fractal
- ^ Theiler, James (1990). "Estimating fractal dimension" (PDF). J. Opt. Soc. Am. A. 7 (6): 1055–73. Bibcode:1990JOSAA...7.1055T. doi:10.1364/JOSAA.7.001055.
- ^ Fractal Generator for ImageJ Archived 20 March 2012 at the Wayback Machine.
- ^ W. Trump, G. Huber, C. Knecht, R. Ziff, to be published
- ^ Monkeys tree fractal curve Archived 21 September 2002 at archive.today
- ^ Fractal dimension of a Penrose tiling
- ^ a b Shishikura, Mitsuhiro (1991). "The Hausdorff dimension of the boundary of the Mandelbrot set and Julia sets". arXiv:math/9201282.
- ^ Lebesgue curve variants
- ^ Duda, Jarek (2008). "Complex base numeral systems". arXiv:0712.1309v3 [math.DS].
- ^ Seuil (1982). Penser les mathématiques. Seuil. ISBN 2-02-006061-2.
- ^ Fractals and the Rössler attractor
- ^ McGuinness, M.J. (1983). "The fractal dimension of the Lorenz attractor". Physics Letters. 99A (1): 5–9. Bibcode:1983PhLA...99....5M. doi:10.1016/0375-9601(83)90052-X.
- ^ Lowe, Thomas (24 October 2016). "Three Variable Dimension Surfaces". ResearchGate.
- ^ The Fractal dimension of the apollonian sphere packing Archived 6 May 2016 at the Wayback Machine
- ^ Baird, Eric (2014). "The Koch curve in three dimensions" – via ResearchGate.
- ^ Hou, B.; Xie, H.; Wen, W.; Sheng, P. (2008). "Three-dimensional metallic fractals and their photonic crystal characteristics" (PDF). Phys. Rev. B. 77 (12): 125113. Bibcode:2008PhRvB..77l5113H. doi:10.1103/PhysRevB.77.125113.
- ^ Hausdorff dimension of the Mandelbulb
- ^ Peter Mörters, Yuval Peres, "Brownian Motion", Cambridge University Press, 2010
- ^ McCartney, Mark; Abernethya, Gavin; Gaulta, Lisa (24 June 2010). "The Divider Dimension of the Irish Coast". Irish Geography. 43 (3): 277–284. doi:10.1080/00750778.2011.582632.
- ^ a b Hutzler, S. (2013). "Fractal Ireland". Science Spin. 58: 19–20. Retrieved 15 November 2016. (See contents page, archived 26 July 2013)
- ^ How long is the coast of Britain? Statistical self-similarity and fractional dimension, B. Mandelbrot
- ^ Lawler, Gregory F.; Schramm, Oded; Werner, Wendelin (2001). "The Dimension of the Planar Brownian Frontier is 4/3". Math. Res. Lett. 8 (4): 401–411. arXiv:math/0010165. Bibcode:2000math.....10165L. doi:10.4310/MRL.2001.v8.n4.a1. S2CID 5877745.
- ^ a b c d e f g h i Sapoval, Bernard (2001). Universalités et fractales. Flammarion-Champs. ISBN 2-08-081466-4.
- ^ Feder, J., "Fractals", Plenum Press, New York, (1988).
- ^ Hull-generating walks
- ^ a b M Sahini; M Sahimi (2003). Applications Of Percolation Theory. CRC Press. ISBN 978-0-203-22153-2.
- ^ Basic properties of galaxy clustering in the light of recent results from the Sloan Digital Sky Survey
- ^ "Power Law Relations". Yale. Archived from the original on 28 June 2010. Retrieved 29 July 2010.
{{cite journal}}: Cite journal requires|journal=(help) - ^ a b Kim, Sang-Hoon (2 February 2008). "Fractal dimensions of a green broccoli and a white cauliflower". arXiv:cond-mat/0411597.
- ^ Kiselev, Valerij G.; Hahn, Klaus R.; Auer, Dorothee P. (2003). "Is the brain cortex a fractal?". NeuroImage. 20 (3): 1765–1774. doi:10.1016/S1053-8119(03)00380-X. PMID 14642486. S2CID 14240006.
- ^ Meakin, Paul (1987). "Diffusion-limited aggregation on multifractal lattices: A model for fluid-fluid displacement in porous media". Physical Review A. 36 (6): 2833–2837. Bibcode:1987PhRvA..36.2833M. doi:10.1103/PhysRevA.36.2833. PMID 9899187.
Further reading[edit]
- Mandelbrot, Benoît (1982). The Fractal Geometry of Nature. W.H. Freeman. ISBN 0-7167-1186-9.
- Peitgen, Heinz-Otto (1988). Saupe, Dietmar (ed.). The Science of Fractal Images. Springer Verlag. ISBN 0-387-96608-0.
- Barnsley, Michael F. (1 January 1993). Fractals Everywhere. Morgan Kaufmann. ISBN 0-12-079061-0.
- Sapoval, Bernard; Mandelbrot, Benoît B. (2001). Universalités et fractales: jeux d'enfant ou délits d'initié?. Flammarion-Champs. ISBN 2-08-081466-4.






















![{\displaystyle \left[1/2,1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/635e14e3bc1abcf9957dc353f1d07a386f3877aa)








![{\displaystyle {\begin{aligned}&2\log _{2}\left(\displaystyle {\frac {{\sqrt[{3}]{27-3{\sqrt {78}}}}+{\sqrt[{3}]{27+3{\sqrt {78}}}}}{3}}\right),\\&{\text{or root of }}2^{x}-1=2^{(2-x)/2}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9184b4b4ffd1eefd0a43ef5eae913f021d5a5d4)






![{\displaystyle f:[0,1]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/2de6d0d4c98d4ca7ad937c772dc3e3e914b062f5)





![{\displaystyle \log _{2}\left({\frac {1+{\sqrt[{3}]{73-6{\sqrt {87}}}}+{\sqrt[{3}]{73+6{\sqrt {87}}}}}{3}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d42ecb0f669d64f67890088232da1d81b39a781)


![{\displaystyle \log _{\sqrt[{\varphi }]{\varphi }}(\varphi )=\varphi }](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca4535f263c345b4e2b2d2200a5aba677ec5c3c3)















![{\displaystyle z_{n+1}=a+bz_{n}\exp \left[i\left[k-p/\left(1+\lfloor z_{n}\rfloor ^{2}\right)\right]\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd6c259da554c2087921ea97191d49338ad11060)




![{\displaystyle {\frac {\log(4)}{\log(2+2\cos(a))}}\in [1,2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd696e5f817b1d222641bb0e05ffc17f88d11096)








































































