Magnus effect

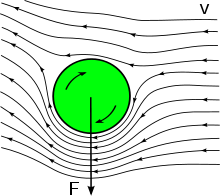
The Magnus effect or Magnus force^[1] is the phenomenon whereby a spinning object flying in a fluid creates a whirlpool of fluid around itself, and experiences a force perpendicular to the line of motion. The overall behaviour is similar to that around an airfoil (see lift force) with a circulation which is generated by the mechanical rotation, rather than by aerofoil action.^[2] The Magnus effect is often considered a demonstration of Bernoulli's principle, but this is incorrect, as the viscosity of the air — assumed to be negligible in Bernoulli's principle — is central to understanding the magnitude of the force.^[3]^[4]

In many ball sports, the Magnus effect is responsible for the curved motion of a spinning ball. The effect also affects spinning missiles, and is used in rotor ships and Flettner aeroplanes.

Principle

When a body (such as a sphere or circular cylinder) is spinning in a viscous fluid, it creates a boundary layer around itself, and the boundary layer induces a more widespread circular motion of the fluid. If the body is moving through the fluid with a velocity V, the velocity of the thin layer of fluid close to the body is a little less than V on the forward-moving side and a little greater than V on the backward-moving side. This is because the induced velocity due to the boundary layer surrounding the spinning body is subtracted from V on the forward-moving side, and added to V on the backward-moving side. If the spinning body is regarded as an inefficient air pump, air will build up on the forward-moving side causing higher pressure there than on the opposite side. Another explanation of the Magnus effect is since there is less (forward) acceleration of air on the forward-moving side than the backward-moving side, there is more pressure on the forward-moving side, resulting in a perpendicular component of force from the air towards the backward-moving side. This layer of spinning air, however, is very thin, and it is more likely that most of the Magnus effect is due to the earlier detachment of the air flow on the forward-moving side, which results in a diversion of the flow (acceleration of air) with a perpendicular component towards the forward-moving side, coexisting with an opposing aerodynamic force with a perpendicular component towards the backward-moving side.^[5]

History

German physicist Heinrich Magnus described the effect in 1852.^[6] However, in 1672, Isaac Newton had described it and correctly inferred the cause after observing tennis players in his Cambridge college.^[7]^[8] In 1742, Benjamin Robins, a British artillery engineer, explained deviations in the trajectories of musket balls in terms of the Magnus effect.^[9]^[10]

Calculation of Magnus force

Given the angular velocity vector ${\vec {\omega }}$ and velocity ${\vec {v}}$ of the object, the resulting force ${\vec {F}}_{M}$ can be calculated using the following formula:

${\vec {F}}_{M}=\mathrm {S} ({\vec {\omega }}\times {\vec {v}})$

where $\mathrm {S}$ is dependent on the average of the air resistance coefficient across the surface of the object.^[11] The $\times$ denotes the vector cross product.

An example of spin ball in the air

The following equation demonstrates the lift force induced on a ball that is spinning along an axis of rotation perpendicular to the direction of its translational motion:

{F}={\frac {1}{2}}\rho v^{2}A\mathrm {C} _{L}

F = lift force

$\rho$ = density of the fluid

v = velocity of the ball

A = cross-sectional area of ball

C_L = lift coefficient

The lift coefficient C_L may be determined from graphs of experimental data using Reynolds numbers and spin ratios.^[12] For a smooth ball with spin ratio of 0.5 to 4.5, typical lift coefficients range from 0.2 to 0.6.

In sport

The Magnus effect explains commonly observed deviations from the typical trajectories or paths of spinning balls in sport, notably association football (soccer), table tennis, tennis,^[13] volleyball, golf, baseball, cricket and in paintball marker balls.

The curved path of a golf ball known as slice or hook is due largely to the ball's spinning motion (about its vertical axis) and the Magnus effect, causing a horizontal force that moves the ball from a straight-line in its trajectory.^[14] Back-spin (upper surface rotating backwards from the direction of movement) on a golf ball causes a vertical force that counteracts the force of gravity slightly, and enables the ball to remain airborne a little longer than it would were the ball not spinning: this allows the ball to travel farther than a non-spinning (about its horizontal axis) ball.

In table tennis, the Magnus effect is easily observed, because of the small mass and low density of the ball. An experienced player can place a wide variety of spins on the ball. Table tennis rackets usually have a surface made of rubber to give the racket maximum grip on the ball, to impart a spin.

The Magnus effect is not responsible for the movement of the cricket ball seen in swing bowling,^[15] although it does contribute to the motion known as drift in spin bowling.

In airsoft, a system known as Hop-Up is used to create a back-spin on a fired BB, which will greatly increase its range, using the Magnus effect in a similar manner as in golf.

In baseball, the spin of a baseball from a pitch influences the air running by a ball, creating low air pressure on one side of the ball; the ball will tend to curve toward the direction of low-pressure side of the ball. The PITCHf/x system measures the change in trajectory caused by Magnus in all pitches thrown in Major League Baseball.^[16]

In external ballistics

The Magnus effect can also be found in advanced external ballistics. Firstly, a spinning bullet in flight is often subject to a crosswind, which can be simplified as blowing either from the left or the right. In addition to this, even in completely calm air a bullet experiences a small sideways wind component due to its yawing motion. This yawing motion along the bullet's flight path means that the nose of the bullet is pointing in a slightly different direction from the direction in which the bullet is travelling. In other words, the bullet is "skidding" sideways at any given moment, and thus it experiences a small sideways wind component in addition to any crosswind component.^[17]

The combined sideways wind component of these two effects causes a Magnus force to act on the bullet, which is perpendicular both to the direction the bullet is pointing and the combined sideways wind. In a very simple case where we ignore various complicating factors, the Magnus force from the crosswind would cause an upward or downward force to act on the spinning bullet (depending on the left or right wind and rotation), causing an observable deflection in the bullet's flight path up or down, thus changing the point of impact.

Overall, the effect of the Magnus force on a bullet's flight path itself is usually insignificant compared to other forces such as aerodynamic drag. However, it greatly affects the bullet's stability, which in turn affects the amount of drag, how the bullet behaves upon impact, and many other factors. The stability of the bullet is affected^{[citation needed]} because the Magnus effect acts on the bullet's centre of pressure instead of its centre of gravity. This means that it affects the yaw angle of the bullet: it tends to twist the bullet along its flight path, either towards the axis of flight (decreasing the yaw thus stabilizing the bullet) or away from the axis of flight (increasing the yaw thus destabilizing the bullet). The critical factor is the location of the centre of pressure, which depends on the flowfield structure, which in turn depends mainly on the bullet's speed (supersonic or subsonic), but also the shape, air density and surface features. If the centre of pressure is ahead of the centre of gravity, the effect is destabilizing; if the centre of pressure is behind the centre of gravity, the effect is stabilizing.^{[citation needed]}

In flying machines

Some flying machines use the Magnus effect to create lift with a rotating cylinder at the front of a wing that allows flight at lower horizontal speeds.^[18] The earliest attempt to use the Magnus Effect for a heavier than air aircraft being in 1910 by a US member of Congress, Butler Ames of Massachusetts, the next attempt was in the early 1930s by three inventors in New York state.^[19]

Magenn Power Inc created a lighter-than-air high altitude wind turbine called MARS that uses the Magnus effect to keep a stable and controlled position in air. MARS meets FAA and Transport Canada guidelines.^[20]

The iCar 101 project uses the Magnus effect in a roadable aircraft design.^[21]

In astronomy

Many astronomical objects (planets, galaxies etc.) have both rotational (spinning) and linear (moving) motions in space. The Magnus force should in principle be acting on astronomical objects passing through a medium like solar wind. There have been arguments indicating that Magnus effect works on planets and galaxies.^[22]^[23]

2010 FIFA World Cup match ball

The match ball for the 2010 FIFA World Cup has been criticised for the different Magnus effect from previous match balls. The current ball is described as having less Magnus effect and as a result flies farther but with less controllable swerve.^[24] Additionally, some say ^[who?] that the ball's Magnus effect varies depending upon the axis on which it spins.

References

^ The Magnus force, Richard Fitzpatrick, Professor of Physics, The University of Texas at Austin
^ Clancy, L.J., Aerodynamics, Section 4.6
^ The Science of Soccer by John Wesson (Institute of Physics Press, Bristol), 2002 p65
^ "Note that it is incorrect to use the Bernoulli effect in explaining this demonstration. The effect is due to shedding of vortexes, NOT to squeezing of flow lines that create a lower pressure on one side of the cylinder compared with the other." UNIVERSITY OF MARYLAND PHYSICS LECTURE-DEMONSTRATION FACILITY http://www.physics.umd.edu/lecdem/services/demos/demosf5/f5-31.htm
^ http://web.archive.org/web/20071018203238/http://www.geocities.com/k_achutarao/MAGNUS/magnus.html
^ G. Magnus (1852) "Über die Abweichung der Geschosse," Abhandlungen der Königlichen Akademie der Wissenschaften zu Berlin, pages 1-23. See also: Gustav Magnus (1853) "Über die Abweichung der Geschosse, und: Über eine abfallende Erscheinung bei rotierenden Körpern" (On the deviation of projectiles, and: On a sinking phenomenon among rotating bodies), Annalen der Physik, vol. 164, no. 1, pages 1-29.
^ Isaac Newton, "A letter of Mr. Isaac Newton, of the University of Cambridge, containing his new theory about light and color," Philosophical Transactions of the Royal Society, vol. 7, pages 3075-3087 (1671-1672). (Note: In this letter, Newton tried to explain the refraction of light by arguing that rotating particles of light curve as they moved through a medium just as a rotating tennis ball curves as it moves through the air.)
^ Gleick, James. 2004. Isaac Newton. London: Harper Fourth Estate.
^ Benjamin Robins, New Principles of Gunnery: Containing the Determinations of the Force of Gun-powder and Investigations of the Difference in the Resisting Power of the Air to Swift and Slow Motions (London: J. Nourse, 1742). (On page 208 of the 1805 edition of Robins' New Principles of Gunnery, Robins describes the experiment in which he observed the Magnus effect: A ball was suspended by a tether consisting of two strings twisted together, and the ball was made to swing. As the strings unwound, the swinging ball rotated, and the plane of its swing also rotated. The direction in which the plane rotated depended on the direction in which the ball rotated.) See also: Tom Holmberg, "Artillery Swings Like a Pendulum..." in "The Napoleon Series". Available on-line at: http://www.napoleon-series.org/military/organization/c_velocity.html . See also: Steele, Brett D. (April 1994) "Muskets and pendulums: Benjamin Robins, Leonhard Euler, and the ballistics revolution," Technology and Culture, vol. 35, no. 2, pages 348-382.
^ Newton's and Robins' observations of the Magnus effect are reproduced in: Peter Guthrie Tait (1893) "On the path of a rotating spherical projectile," Transactions of the Royal Society of Edinburgh, vol. 37, pages 427-440.
^ http://fy.chalmers.se/~f3aamp/f1/bollprojekt/fotboll.pdf
^ Bearman, P W, and J K Harvey. "Golf Ball Aerodynamics." Aeronautical Quarterly. XXVII. (1976):112-122. Print.
^ Lord Rayleigh (1877) "On the irregular flight of a tennis ball," Messenger of Mathematics, vol. 7, pages 14–16.
^ Clancy, L.J., Aerodynamics, Section 4.5
^ Clancy, L.J., Aerodynamics, Figure 4.19
^ Nathan, Alan M. (18 October 2012). "Determining Pitch Movement from PITCHf/x Data" (PDF). Retrieved 18 October 2012.
^ Yaw of repose
^ NASA - Lift on rotating cylinders
^ "Whirling Spools Lift This Plane", November 1930, Popular Science
^ Magenn Power Inc Website
^ iCar 101 roadable aircraft
^ Omar, Amitesh (10 May 2011). "A possibility of Magnus effect on disk galaxies" (PDF). Current Science. 100 (9). ISSN 0011-3891. Retrieved 8 November 2012.
^ Pérez-de-Tejada, H. (2008). "Viscous Magnus Force for the Rotating Venus Ionosphere". The Astrophysical Journal. Letters. 676 (1): L65–L68. doi:10.1086/529518. Retrieved 8 November 2012. {{cite journal}}: Unknown parameter |month= ignored (help)
^ SBS 2010 FIFA World Cup Show interview 22 June 2010 10:30pm by Craig Johnston

External links

[1] The Magnus force, Richard Fitzpatrick, Professor of Physics, The University of Texas at Austin

[2] Clancy, L.J., Aerodynamics, Section 4.6

[3] The Science of Soccer by John Wesson (Institute of Physics Press, Bristol), 2002 p65

[4] "Note that it is incorrect to use the Bernoulli effect in explaining this demonstration. The effect is due to shedding of vortexes, NOT to squeezing of flow lines that create a lower pressure on one side of the cylinder compared with the other." UNIVERSITY OF MARYLAND PHYSICS LECTURE-DEMONSTRATION FACILITY http://www.physics.umd.edu/lecdem/services/demos/demosf5/f5-31.htm

[5] ttp://web.archive.org/web/20071018203238/http://www.geocities.com/k_achutarao/MAGNUS/magnus.html

[6] G. Magnus (1852) "Über die Abweichung der Geschosse," Abhandlungen der Königlichen Akademie der Wissenschaften zu Berlin, pages 1-23. See also: Gustav Magnus (1853) "Über die Abweichung der Geschosse, und: Über eine abfallende Erscheinung bei rotierenden Körpern" (On the deviation of projectiles, and: On a sinking phenomenon among rotating bodies), Annalen der Physik, vol. 164, no. 1, pages 1-29.

[7] Isaac Newton, "A letter of Mr. Isaac Newton, of the University of Cambridge, containing his new theory about light and color," Philosophical Transactions of the Royal Society, vol. 7, pages 3075-3087 (1671-1672). (Note: In this letter, Newton tried to explain the refraction of light by arguing that rotating particles of light curve as they moved through a medium just as a rotating tennis ball curves as it moves through the air.)

[8] Gleick, James. 2004. Isaac Newton. London: Harper Fourth Estate.

[9] Benjamin Robins, New Principles of Gunnery: Containing the Determinations of the Force of Gun-powder and Investigations of the Difference in the Resisting Power of the Air to Swift and Slow Motions (London: J. Nourse, 1742). (On page 208 of the 1805 edition of Robins' New Principles of Gunnery, Robins describes the experiment in which he observed the Magnus effect: A ball was suspended by a tether consisting of two strings twisted together, and the ball was made to swing. As the strings unwound, the swinging ball rotated, and the plane of its swing also rotated. The direction in which the plane rotated depended on the direction in which the ball rotated.) See also: Tom Holmberg, "Artillery Swings Like a Pendulum..." in "The Napoleon Series". Available on-line at: http://www.napoleon-series.org/military/organization/c_velocity.html . See also: Steele, Brett D. (April 1994) "Muskets and pendulums: Benjamin Robins, Leonhard Euler, and the ballistics revolution," Technology and Culture, vol. 35, no. 2, pages 348-382.

[10] Newton's and Robins' observations of the Magnus effect are reproduced in: Peter Guthrie Tait (1893) "On the path of a rotating spherical projectile," Transactions of the Royal Society of Edinburgh, vol. 37, pages 427-440.

[11] ttp://fy.chalmers.se/~f3aamp/f1/bollprojekt/fotboll.pdf

[12] Bearman, P W, and J K Harvey. "Golf Ball Aerodynamics." Aeronautical Quarterly. XXVII. (1976):112-122. Print.

[13] Lord Rayleigh (1877) "On the irregular flight of a tennis ball," Messenger of Mathematics, vol. 7, pages 14–16.

[14] Clancy, L.J., Aerodynamics, Section 4.5

[15] Clancy, L.J., Aerodynamics, Figure 4.19

[16] Nathan, Alan M. (18 October 2012). "Determining Pitch Movement from PITCHf/x Data" (PDF). Retrieved 18 October 2012.

[17] Yaw of repose

[18] NASA - Lift on rotating cylinders

[19] "Whirling Spools Lift This Plane", November 1930, Popular Science

[20] Magenn Power Inc Website

[21] Car 101 roadable aircraft

[22] Omar, Amitesh (10 May 2011). "A possibility of Magnus effect on disk galaxies" (PDF). Current Science. 100 (9). ISSN 0011-3891. Retrieved 8 November 2012.

[23] Pérez-de-Tejada, H. (2008). "Viscous Magnus Force for the Rotating Venus Ionosphere". The Astrophysical Journal. Letters. 676 (1): L65–L68. doi:10.1086/529518. Retrieved 8 November 2012. {{cite journal}}: Unknown parameter |month= ignored (help)

[24] SBS 2010 FIFA World Cup Show interview 22 June 2010 10:30pm by Craig Johnston

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]