Stericated 5-simplexes
  5-simplex |
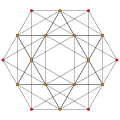  Stericated 5-simplex | ||
  Steritruncated 5-simplex |
  Stericantellated 5-simplex | ||
  Stericantitruncated 5-simplex |
  Steriruncitruncated 5-simplex | ||
  Steriruncicantitruncated 5-simplex (Omnitruncated 5-simplex) | |||
| Orthogonal projections in A5 and A4 Coxeter planes | |||
|---|---|---|---|
In five-dimensional geometry, a stericated 5-simplex is a convex uniform 5-polytope with fourth-order truncations (sterication) of the regular 5-simplex.
There are six unique sterications of the 5-simplex, including permutations of truncations, cantellations, and runcinations. The simplest stericated 5-simplex is also called an expanded 5-simplex, with the first and last nodes ringed, for being constructible by an expansion operation applied to the regular 5-simplex. The highest form, the steriruncicantitruncated 5-simplex is more simply called an omnitruncated 5-simplex with all of the nodes ringed.
Stericated 5-simplex
[edit]| Stericated 5-simplex | ||
| Type | Uniform 5-polytope | |
| Schläfli symbol | 2r2r{3,3,3,3} 2r{32,2} = | |
| Coxeter-Dynkin diagram | or | |
| 4-faces | 62 | 6+6 {3,3,3} 15+15 {}×{3,3} 20 {3}×{3} |
| Cells | 180 | 60 {3,3} 120 {}×{3} |
| Faces | 210 | 120 {3} 90 {4} |
| Edges | 120 | |
| Vertices | 30 | |
| Vertex figure |  Tetrahedral antiprism | |
| Coxeter group | A5×2, [[3,3,3,3]], order 1440 | |
| Properties | convex, isogonal, isotoxal | |
A stericated 5-simplex can be constructed by an expansion operation applied to the regular 5-simplex, and thus is also sometimes called an expanded 5-simplex. It has 30 vertices, 120 edges, 210 faces (120 triangles and 90 squares), 180 cells (60 tetrahedra and 120 triangular prisms) and 62 4-faces (12 5-cells, 30 tetrahedral prisms and 20 3-3 duoprisms).
Alternate names
[edit]- Expanded 5-simplex
- Stericated hexateron
- Small cellated dodecateron (Acronym: scad) (Jonathan Bowers)[1]
Cross-sections
[edit]The maximal cross-section of the stericated hexateron with a 4-dimensional hyperplane is a runcinated 5-cell. This cross-section divides the stericated hexateron into two pentachoral hypercupolas consisting of 6 5-cells, 15 tetrahedral prisms and 10 3-3 duoprisms each.
Coordinates
[edit]The vertices of the stericated 5-simplex can be constructed on a hyperplane in 6-space as permutations of (0,1,1,1,1,2). This represents the positive orthant facet of the stericated 6-orthoplex.
A second construction in 6-space, from the center of a rectified 6-orthoplex is given by coordinate permutations of:
- (1,-1,0,0,0,0)
The Cartesian coordinates in 5-space for the normalized vertices of an origin-centered stericated hexateron are:
Root system
[edit]Its 30 vertices represent the root vectors of the simple Lie group A5. It is also the vertex figure of the 5-simplex honeycomb.
Images
[edit]| Ak Coxeter plane |
A5 | A4 |
|---|---|---|
| Graph | 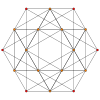
|

|
| Dihedral symmetry | [6] | [[5]]=[10] |
| Ak Coxeter plane |
A3 | A2 |
| Graph | 
|

|
| Dihedral symmetry | [4] | [[3]]=[6] |
 orthogonal projection with [6] symmetry |
Steritruncated 5-simplex
[edit]| Steritruncated 5-simplex | ||
| Type | Uniform 5-polytope | |
| Schläfli symbol | t0,1,4{3,3,3,3} | |
| Coxeter-Dynkin diagram | ||
| 4-faces | 62 | 6 t{3,3,3} 15 {}×t{3,3} 20 {3}×{6} 15 {}×{3,3} 6 t0,3{3,3,3} |
| Cells | 330 | |
| Faces | 570 | |
| Edges | 420 | |
| Vertices | 120 | |
| Vertex figure | 
| |
| Coxeter group | A5 [3,3,3,3], order 720 | |
| Properties | convex, isogonal | |
Alternate names
[edit]- Steritruncated hexateron
- Celliprismated hexateron (Acronym: cappix) (Jonathan Bowers)[2]
Coordinates
[edit]The coordinates can be made in 6-space, as 180 permutations of:
- (0,1,1,1,2,3)
This construction exists as one of 64 orthant facets of the steritruncated 6-orthoplex.
Images
[edit]| Ak Coxeter plane |
A5 | A4 |
|---|---|---|
| Graph | 
|

|
| Dihedral symmetry | [6] | [5] |
| Ak Coxeter plane |
A3 | A2 |
| Graph | 
|

|
| Dihedral symmetry | [4] | [3] |
Stericantellated 5-simplex
[edit]| Stericantellated 5-simplex | ||
| Type | Uniform 5-polytope | |
| Schläfli symbol | t0,2,4{3,3,3,3} | |
| Coxeter-Dynkin diagram | or | |
| 4-faces | 62 | 12 rr{3,3,3} 30 rr{3,3}x{} 20 {3}×{3} |
| Cells | 420 | 60 rr{3,3} 240 {}×{3} 90 {}×{}×{} 30 r{3,3} |
| Faces | 900 | 360 {3} 540 {4} |
| Edges | 720 | |
| Vertices | 180 | |
| Vertex figure | 
| |
| Coxeter group | A5×2, [[3,3,3,3]], order 1440 | |
| Properties | convex, isogonal | |
Alternate names
[edit]- Stericantellated hexateron
- Cellirhombated dodecateron (Acronym: card) (Jonathan Bowers)[3]
Coordinates
[edit]The coordinates can be made in 6-space, as permutations of:
- (0,1,1,2,2,3)
This construction exists as one of 64 orthant facets of the stericantellated 6-orthoplex.
Images
[edit]| Ak Coxeter plane |
A5 | A4 |
|---|---|---|
| Graph | 
|

|
| Dihedral symmetry | [6] | [[5]]=[10] |
| Ak Coxeter plane |
A3 | A2 |
| Graph | 
|

|
| Dihedral symmetry | [4] | [[3]]=[6] |
Stericantitruncated 5-simplex
[edit]| Stericantitruncated 5-simplex | ||
| Type | Uniform 5-polytope | |
| Schläfli symbol | t0,1,2,4{3,3,3,3} | |
| Coxeter-Dynkin diagram | ||
| 4-faces | 62 | |
| Cells | 480 | |
| Faces | 1140 | |
| Edges | 1080 | |
| Vertices | 360 | |
| Vertex figure | 
| |
| Coxeter group | A5 [3,3,3,3], order 720 | |
| Properties | convex, isogonal | |
Alternate names
[edit]- Stericantitruncated hexateron
- Celligreatorhombated hexateron (Acronym: cograx) (Jonathan Bowers)[4]
Coordinates
[edit]The coordinates can be made in 6-space, as 360 permutations of:
- (0,1,1,2,3,4)
This construction exists as one of 64 orthant facets of the stericantitruncated 6-orthoplex.
Images
[edit]| Ak Coxeter plane |
A5 | A4 |
|---|---|---|
| Graph | 
|

|
| Dihedral symmetry | [6] | [5] |
| Ak Coxeter plane |
A3 | A2 |
| Graph | 
|

|
| Dihedral symmetry | [4] | [3] |
Steriruncitruncated 5-simplex
[edit]| Steriruncitruncated 5-simplex | ||
| Type | Uniform 5-polytope | |
| Schläfli symbol | t0,1,3,4{3,3,3,3} 2t{32,2} | |
| Coxeter-Dynkin diagram | or | |
| 4-faces | 62 | 12 t0,1,3{3,3,3} 30 {}×t{3,3} 20 {6}×{6} |
| Cells | 450 | |
| Faces | 1110 | |
| Edges | 1080 | |
| Vertices | 360 | |
| Vertex figure | 
| |
| Coxeter group | A5×2, [[3,3,3,3]], order 1440 | |
| Properties | convex, isogonal | |
Alternate names
[edit]- Steriruncitruncated hexateron
- Celliprismatotruncated dodecateron (Acronym: captid) (Jonathan Bowers)[5]
Coordinates
[edit]The coordinates can be made in 6-space, as 360 permutations of:
- (0,1,2,2,3,4)
This construction exists as one of 64 orthant facets of the steriruncitruncated 6-orthoplex.
Images
[edit]| Ak Coxeter plane |
A5 | A4 |
|---|---|---|
| Graph | 
|

|
| Dihedral symmetry | [6] | [[5]]=[10] |
| Ak Coxeter plane |
A3 | A2 |
| Graph | 
|

|
| Dihedral symmetry | [4] | [[3]]=[6] |
Omnitruncated 5-simplex
[edit]| Omnitruncated 5-simplex | ||
| Type | Uniform 5-polytope | |
| Schläfli symbol | t0,1,2,3,4{3,3,3,3} 2tr{32,2} | |
| Coxeter-Dynkin diagram |
or | |
| 4-faces | 62 | 12 t0,1,2,3{3,3,3} 30 {}×tr{3,3} 20 {6}×{6} |
| Cells | 540 | 360 t{3,4} 90 {4,3} 90 {}×{6} |
| Faces | 1560 | 480 {6} 1080 {4} |
| Edges | 1800 | |
| Vertices | 720 | |
| Vertex figure |  Irregular 5-cell | |
| Coxeter group | A5×2, [[3,3,3,3]], order 1440 | |
| Properties | convex, isogonal, zonotope | |
The omnitruncated 5-simplex has 720 vertices, 1800 edges, 1560 faces (480 hexagons and 1080 squares), 540 cells (360 truncated octahedra, 90 cubes, and 90 hexagonal prisms), and 62 4-faces (12 omnitruncated 5-cells, 30 truncated octahedral prisms, and 20 6-6 duoprisms).
Alternate names
[edit]- Steriruncicantitruncated 5-simplex (Full description of omnitruncation for 5-polytopes by Johnson)
- Omnitruncated hexateron
- Great cellated dodecateron (Acronym: gocad) (Jonathan Bowers)[6]
Coordinates
[edit]The vertices of the omnitruncated 5-simplex can be most simply constructed on a hyperplane in 6-space as permutations of (0,1,2,3,4,5). These coordinates come from the positive orthant facet of the steriruncicantitruncated 6-orthoplex, t0,1,2,3,4{34,4}, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Images
[edit]| Ak Coxeter plane |
A5 | A4 |
|---|---|---|
| Graph | 
|

|
| Dihedral symmetry | [6] | [[5]]=[10] |
| Ak Coxeter plane |
A3 | A2 |
| Graph | 
|

|
| Dihedral symmetry | [4] | [[3]]=[6] |

Permutohedron
[edit]The omnitruncated 5-simplex is the permutohedron of order 6. It is also a zonotope, the Minkowski sum of six line segments parallel to the six lines through the origin and the six vertices of the 5-simplex.
 Orthogonal projection, vertices labeled as a permutohedron. |
Related honeycomb
[edit]The omnitruncated 5-simplex honeycomb is constructed by omnitruncated 5-simplex facets with 3 facets around each ridge. It has Coxeter-Dynkin diagram of ![]()
![]()
![]()
![]()
![]() .
.
| Coxeter group | |||||
|---|---|---|---|---|---|
| Coxeter-Dynkin | |||||
| Picture | 
|

|
|||
| Name | Apeirogon | Hextille | Omnitruncated 3-simplex honeycomb |
Omnitruncated 4-simplex honeycomb |
Omnitruncated 5-simplex honeycomb |
| Facets | 
|

|

|
|

|
Full snub 5-simplex
[edit]The full snub 5-simplex or omnisnub 5-simplex, defined as an alternation of the omnitruncated 5-simplex is not uniform, but it can be given Coxeter diagram ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() and symmetry [[3,3,3,3]]+, and constructed from 12 snub 5-cells, 30 snub tetrahedral antiprisms, 20 3-3 duoantiprisms, and 360 irregular 5-cells filling the gaps at the deleted vertices.
and symmetry [[3,3,3,3]]+, and constructed from 12 snub 5-cells, 30 snub tetrahedral antiprisms, 20 3-3 duoantiprisms, and 360 irregular 5-cells filling the gaps at the deleted vertices.
Related uniform polytopes
[edit]These polytopes are a part of 19 uniform 5-polytopes based on the [3,3,3,3] Coxeter group, all shown here in A5 Coxeter plane orthographic projections. (Vertices are colored by projection overlap order, red, orange, yellow, green, cyan, blue, purple having progressively more vertices)
| A5 polytopes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
 t0 |
 t1 |
 t2 |
 t0,1 |
 t0,2 |
 t1,2 |
 t0,3 | |||||
 t1,3 |
 t0,4 |
 t0,1,2 |
 t0,1,3 |
 t0,2,3 |
 t1,2,3 |
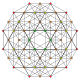 t0,1,4 | |||||
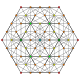 t0,2,4 |
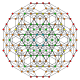 t0,1,2,3 |
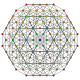 t0,1,2,4 |
 t0,1,3,4 |
 t0,1,2,3,4 | |||||||
Notes
[edit]References
[edit]- H.S.M. Coxeter:
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D.
- Klitzing, Richard. "5D uniform polytopes (polytera)". x3o3o3o3x - scad, x3x3o3o3x - cappix, x3o3x3o3x - card, x3x3x3o3x - cograx, x3x3o3x3x - captid, x3x3x3x3x - gocad
External links
[edit]- Glossary for hyperspace, George Olshevsky.
- Polytopes of Various Dimensions
- Multi-dimensional Glossary














