Rationalizable strategy
| Rationalizability | |
|---|---|
| Solution concept in game theory | |
| Relationship | |
| Subset of | Dominant strategy equilibrium |
| Superset of | Nash equilibrium |
| Significance | |
| Proposed by | D. Bernheim and D. Pearce |
| Example | Matching pennies |
Rationalizability is a solution concept in game theory. It is the most permissive possible solution concept that still requires both players to be at least somewhat rational and know the other players are also somewhat rational, i.e. that they do not play dominated strategies. A strategy is rationalizable if there exists some possible set of beliefs both players could have about each other's actions, that would still result in the strategy being played.
Rationalizability is a broader concept than a Nash equilibrium. Both require players to respond optimally to some belief about their opponents' actions, but Nash equilibrium requires these beliefs to be correct, while rationalizability does not. Rationalizability was first defined, independently, by Bernheim (1984) and Pearce (1984).
Definition
[edit]Starting with a normal-form game, the rationalizable set of actions can be computed as follows:
- Start with the full action set for each player.
- Remove all dominated strategies, i.e. strategies that "never make sense" (are never a best reply to any belief about the opponents' actions). The motivation for this step is no rational player would ever choose such actions.
- Remove all actions which are never a best reply to any belief about the opponents' remaining actions—this second step is justified because each player knows that the other players are rational.
- Continue the process until no further actions can be eliminated.
In a game with finitely many actions, this process always terminates and leaves a non-empty set of actions for each player. These are the rationalizable actions.
Iterated elimination of strictly dominated strategies (IESDS)
[edit]The iterated elimination (or deletion, or removal) of dominated strategies (also denominated as IESDS, or IDSDS, or IRSDS) is one common technique for solving games that involves iteratively removing dominated strategies. In the first step, at most one dominated strategy is removed from the strategy space of each of the players since no rational player would ever play these strategies. This results in a new, smaller game. Some strategies—that were not dominated before—may be dominated in the smaller game. The first step is repeated, creating a new even smaller game, and so on. The process stops when no dominated strategy is found for any player. This process is valid since it is assumed that rationality among players is common knowledge, that is, each player knows that the rest of the players are rational, and each player knows that the rest of the players know that he knows that the rest of the players are rational, and so on ad infinitum (see Aumann, 1976).
There are two versions of this process. One version involves only eliminating strictly dominated strategies. If, after completing this process, there is only one strategy for each player remaining, that strategy set is the unique Nash equilibrium.[1] Moreover, iterated elimination of strictly dominated strategies is path independent. That is, if at any point in the process there are multiple strictly dominated strategies, then it doesn't matter for the end result which strategies we remove first.[2]
Strict Dominance Deletion Step-by-Step Example:

- C is strictly dominated by A for Player 1. Therefore, Player 1 will never play strategy C. Player 2 knows this. (see IESDS Figure 1)
- Of the remaining strategies (see IESDS Figure 2), Z is strictly dominated by Y and X for Player 2. Therefore, Player 2 will never play strategy Z. Player 1 knows this.
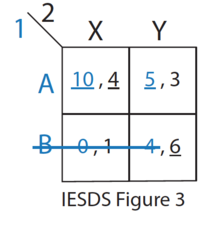
- Of the remaining strategies (see IESDS Figure 3), B is strictly dominated by A for Player 1. Therefore, Player 1 will never play B. Player 2 knows this.
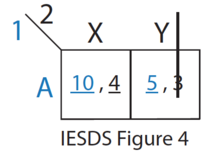
- Of the remaining strategies (see IESDS Figure 4), Y is strictly dominated by X for Player 2. Therefore, Player 2 will never play Y. Player 1 knows this.
- Only one rationalizable strategy is left {A,X} which results in a payoff of (10,4). This is the single Nash Equilibrium for this game.
Another version involves eliminating both strictly and weakly dominated strategies. If, at the end of the process, there is a single strategy for each player, this strategy set is also a Nash equilibrium. However, unlike the first process, elimination of weakly dominated strategies may eliminate some Nash equilibria. As a result, the Nash equilibrium found by eliminating weakly dominated strategies may not be the only Nash equilibrium. (In some games, if we remove weakly dominated strategies in a different order, we may end up with a different Nash equilibrium.)
Weak Dominance Deletion Step-by-Step Example:
- O is strictly dominated by N for Player 1. Therefore, Player 1 will never play strategy O. Player 2 knows this. (see IESDS Figure 5)
- U is weakly dominated by T for Player 2. If Player 2 chooses T, then the final equilibrium is (N,T)
- O is strictly dominated by N for Player 1. Therefore, Player 1 will never play strategy O. Player 2 knows this. (see IESDS Figure 6)
- T is weakly dominated by U for Player 2. If Player 2 chooses U, then the final equilibrium is (N,U)
In any case, if by iterated elimination of dominated strategies there is only one strategy left for each player, the game is called a dominance-solvable game.
Iterated elimination by mixed strategy
[edit]There are instances when there is no pure strategy that dominates another pure strategy, but a mixture of two or more pure strategies can dominate another strategy. This is called Strictly Dominant Mixed Strategies. Some authors allow for elimination of strategies dominated by a mixed strategy in this way.
Example 1:
In this scenario, for player 1, there is no pure strategy that dominates another pure strategy. Let's define the probability of player 1 playing up as p, and let p = 1/2. We can set a mixed strategy where player 1 plays up and down with probabilities (1/2,1/2). When player 2 plays left, then the payoff for player 1 playing the mixed strategy of up and down is 1, when player 2 plays right, the payoff for player 1 playing the mixed strategy is 0.5. Thus regardless of whether player 2 chooses left or right, player 1 gets more from playing this mixed strategy between up and down than if the player were to play the middle strategy. In this case, we should eliminate the middle strategy for player 1 since it's been dominated by the mixed strategy of playing up and down with probability (1/2,1/2).
Example 2:
We can demonstrate the same methods on a more complex game and solve for the rational strategies. In this scenario, the blue coloring represents the dominating numbers in the particular strategy.

Step-by-step solving:
For Player 2, X is dominated by the mixed strategy 1/2Y and 1/2Z.
The expected payoff for playing strategy 1/2Y + 1/2Z must be greater than the expected payoff for playing pure strategy X, assigning 1/2 and 1/2 as tester values. The argument for mixed strategy dominance can be made if there is at least one mixed strategy that allows for dominance.
Testing with 1/2 and 1/2 gets the following:
Expected average payoff of 1/2 Strategy Y: 1/2(4+0+4) = 4
Expected average payoff of 1/2 Strategy Z: 1/2(0+5+5) = 5
Expected average payoff of pure strategy X: (1+1+3) = 5
Set up the inequality to determine whether the mixed strategy will dominate the pure strategy based on expected payoffs.
u1/2Y + u1/2Z ⩼ uX
4 + 5 > 5
Mixed strategy 1/2Y and 1/2Z will dominate pure strategy X for Player 2, and thus X can be eliminated from the rationalizable strategies for P2.
For Player 1, U is dominated by the pure strategy D.
For player 2, Y is dominated by the pure strategy Z.
This leaves M dominating D for Player 1.
The only rationalizable strategy for Players 1 and 2 is then (M,Z) or (3,5).
Constraints on beliefs
[edit]| A | B | |
|---|---|---|
| a | 1, 1 | 0, 0 |
| b | 0, 0 | 1, 1 |
Consider a simple coordination game (the payoff matrix is to the right). The row player can play a if he can reasonably believe that the column player could play A, since a is a best response to A. He can reasonably believe that the column player can play A if it is reasonable for the column player to believe that the row player could play a. She can believe that he will play a if it is reasonable for her to believe that he could play a, etc.
| C | D | |
|---|---|---|
| c | 2, 2 | 0, 3 |
| d | 3, 0 | 1, 1 |
This provides an infinite chain of consistent beliefs that result in the players playing (a, A). This makes (a, A) a rationalizable pair of actions. A similar process can be repeated for (b, B).
As an example where not all strategies are rationalizable, consider a prisoner's dilemma pictured to the left. Row player would never play c, since c is not a best response to any strategy by the column player. For this reason, c is not rationalizable.
| L | R | |
|---|---|---|
| t | 3, - | 0, - |
| m | 0, - | 3, - |
| b | 1, - | 1, - |
Conversely, for two-player games, the set of all rationalizable strategies can be found by iterated elimination of strictly dominated strategies. For this method to hold however, one also needs to consider strict domination by mixed strategies. Consider the game on the right with payoffs of the column player omitted for simplicity. Notice that "b" is not strictly dominated by either "t" or "m" in the pure strategy sense, but it is still dominated by a strategy that would mix "t" and "m" with probability of each equal to 1/2. This is due to the fact that given any belief about the action of the column player, the mixed strategy will always yield higher expected payoff.[3] This implies that "b" is not rationalizable.
Moreover, "b" is not a best response to either "L" or "R" or any mix of the two. This is because an action that is not rationalizable can never be a best response to any opponent's strategy (pure or mixed). This would imply another version of the previous method of finding rationalizable strategies as those that survive the iterated elimination of strategies that are never a best response (in pure or mixed sense).
In games with more than two players, however, there may be strategies that are not strictly dominated, but which can never be the best response. By the iterated elimination of all such strategies one can find the rationalizable strategies for a multiplayer game.
Rationalizability and Nash equilibria
[edit]It can be easily proved that a Nash equilibrium is a rationalizable equilibrium; however, the converse is not true. Some rationalizable equilibria are not Nash equilibria. This makes the rationalizability concept a generalization of Nash equilibrium concept.
| H | T | |
|---|---|---|
| h | 1, -1 | -1, 1 |
| t | -1, 1 | 1, -1 |
As an example, consider the game matching pennies pictured to the right. In this game the only Nash equilibrium is row playing h and t with equal probability and column playing H and T with equal probability. However, all pure strategies in this game are rationalizable.
Consider the following reasoning: row can play h if it is reasonable for her to believe that column will play H. Column can play H if its reasonable for him to believe that row will play t. Row can play t if it is reasonable for her to believe that column will play T. Column can play T if it is reasonable for him to believe that row will play h (beginning the cycle again). This provides an infinite set of consistent beliefs that results in row playing h. A similar argument can be given for row playing t, and for column playing either H or T.
See also
[edit]Footnotes
[edit]- ^ Joel., Watson,. Strategy : an introduction to game theory (Second ed.). New York. ISBN 9780393929348.
- ^ Gilboa, I.; Kalai, E.; Zemel, E. (1990). "On the order of eliminating dominated strategies" (PDF). Operations Research Letters. 9 (2): 85–89. doi:10.1016/0167-6377(90)90046-8.
- ^ Gibbons, Robert (1992). A Primer in Game Theory. pp. 32–33.
References
[edit]- Bernheim, D. (1984) Rationalizable Strategic Behavior. Econometrica 52: 1007–1028.
- Fudenberg, Drew and Jean Tirole (1993) Game Theory. Cambridge: MIT Press.
- Pearce, D. (1984) Rationalizable Strategic Behavior and the Problem of Perfection. Econometrica 52: 1029–1050.
- Ratcliff, J. (1992–1997) lecture notes on game theory, §2.2: "Iterated Dominance and Rationalizability"