User:Czech is Cyrillized/EulerNum
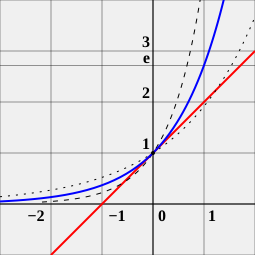
The number e is an important mathematical constant, approximately equal to 2.71828, that is the base of the natural logarithm.[1] It is the limit of (1 + 1/n)n as n becomes large, an expression that arises in the study of compound interest, and can also be calculated as the sum of the infinite series[2]
The constant can be defined in many ways; for example, e is the unique real number such that the value of the derivative (slope of the tangent line) of the function f(x) = ex at the point x = 0 is equal to 1.[3] The function ex so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base e. The natural logarithm of a positive number k can also be defined directly as the area under the curve y = 1/x between x = 1 and x = k, in which case, e is the number whose natural logarithm is 1. There are also more alternative characterizations.
Sometimes called Euler's number after the Swiss mathematician Leonhard Euler, e is not to be confused with γ—the Euler–Mascheroni constant, sometimes called simply Euler's constant. The number e is also known as Napier's constant, but Euler's choice of this symbol is said to have been retained in his honor.[4] The number e is of eminent importance in mathematics,[5] alongside 0, 1, π and i. All five of these numbers play important and recurring roles across mathematics, and are the five constants appearing in one formulation of Euler's identity. Like the constant π, e is irrational: it is not a ratio of integers; and it is transcendental: it is not a root of any non-zero polynomial with rational coefficients. The numerical value of e truncated to 50 decimal places is
| Part of a series of articles on the |
| mathematical constant e |
|---|
 |
| Properties |
| Applications |
| Defining e |
| People |
| Related topics |
History[edit]
The first references to the constant were published in 1618 in the table of an appendix of a work on logarithms by John Napier.[6] However, this did not contain the constant itself, but simply a list of logarithms calculated from the constant. It is assumed that the table was written by William Oughtred. The discovery of the constant itself is credited to Jacob Bernoulli, who attempted to find the value of the following expression (which is in fact e):
The first known use of the constant, represented by the letter b, was in correspondence from Gottfried Leibniz to Christiaan Huygens in 1690 and 1691. Leonhard Euler introduced the letter e as the base for natural logarithms, writing in a letter to Christian Goldbach of 25 November 1731.[7] Euler started to use the letter e for the constant in 1727 or 1728, in an unpublished paper on explosive forces in cannons,[8] and the first appearance of e in a publication was Euler's Mechanica (1736). While in the subsequent years some researchers used the letter c, e was more common and eventually became the standard.
Applications[edit]
Compound interest[edit]

Jacob Bernoulli discovered this constant by studying a question about compound interest:[6]
- An account starts with $1.00 and pays 100 percent interest per year. If the interest is credited once, at the end of the year, the value of the account at year-end will be $2.00. What happens if the interest is computed and credited more frequently during the year?
If the interest is credited twice in the year, the interest rate for each 6 months will be 50%, so the initial $1 is multiplied by 1.5 twice, yielding $1.00×1.52 = $2.25 at the end of the year. Compounding quarterly yields $1.00×1.254 = $2.4414..., and compounding monthly yields $1.00×(1+1/12)12 = $2.613035... If there are n compounding intervals, the interest for each interval will be 100%/n and the value at the end of the year will be $1.00×(1 + 1/n)n.
Bernoulli noticed that this sequence approaches a limit (the force of interest) with larger n and, thus, smaller compounding intervals. Compounding weekly (n = 52) yields $2.692597..., while compounding daily (n = 365) yields $2.714567..., just two cents more. The limit as n grows large is the number that came to be known as e; with continuous compounding, the account value will reach $2.7182818.... More generally, an account that starts at $1 and offers an annual interest rate of R will, after t years, yield eRt dollars with continuous compounding. (Here R is a fraction, so for 5% interest, R = 5/100 = 0.05)
Bernoulli trials[edit]
The number e itself also has applications to probability theory, where it arises in a way not obviously related to exponential growth. Suppose that a gambler plays a slot machine that pays out with a probability of one in n and plays it n times. Then, for large n (such as a million) the probability that the gambler will lose every bet is (approximately) 1/e. For n = 20 it is already 1/2.72.
This is an example of a Bernoulli trials process. Each time the gambler plays the slots, there is a one in one million chance of winning. Playing one million times is modelled by the binomial distribution, which is closely related to the binomial theorem. The probability of winning k times out of a million trials is;
In particular, the probability of winning zero times (k = 0) is
This is very close to the following limit for 1/e:
Derangements[edit]
Another application of e, also discovered in part by Jacob Bernoulli along with Pierre Raymond de Montmort is in the problem of derangements, also known as the hat check problem:[9] n guests are invited to a party, and at the door each guest checks his hat with the butler who then places them into n boxes, each labelled with the name of one guest. But the butler does not know the identities of the guests, and so he puts the hats into boxes selected at random. The problem of de Montmort is to find the probability that none of the hats gets put into the right box. The answer is:
As the number n of guests tends to infinity, pn approaches 1/e. Furthermore, the number of ways the hats can be placed into the boxes so that none of the hats is in the right box is n!/e rounded to the nearest integer, for every positive n.[10]
Asymptotics[edit]
The number e occurs naturally in connection with many problems involving asymptotics. A prominent example is Stirling's formula for the asymptotics of the factorial function, in which both the numbers e and π enter:
A particular consequence of this is
- .
e in calculus[edit]
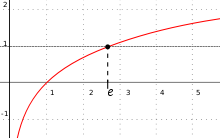
The principal motivation for introducing the number e, particularly in calculus, is to perform differential and integral calculus with exponential functions and logarithms.[11] A general exponential function y = ax has derivative given as the limit:
The limit on the right-hand side is independent of the variable x: it depends only on the base a. When the base is e, this limit is equal to one, and so e is symbolically defined by the equation:
Consequently, the exponential function with base e is particularly suited to doing calculus. Choosing e, as opposed to some other number, as the base of the exponential function makes calculations involving the derivative much simpler.
Another motivation comes from considering the base-a logarithm.[12] Considering the definition of the derivative of loga x as the limit:
where the substitution u = h/x was made in the last step. The last limit appearing in this calculation is again an undetermined limit that depends only on the base a, and if that base is e, the limit is one. So symbolically,
The logarithm in this special base is called the natural logarithm and is represented as ln; it behaves well under differentiation since there is no undetermined limit to carry through the calculations.
There are thus two ways in which to select a special number a = e. One way is to set the derivative of the exponential function ax to ax, and solve for a. The other way is to set the derivative of the base a logarithm to 1/x and solve for a. In each case, one arrives at a convenient choice of base for doing calculus. In fact, these two solutions for a are actually the same, the number e.
Alternative characterizations[edit]

Other characterizations of e are also possible: one is as the limit of a sequence, another is as the sum of an infinite series, and still others rely on integral calculus. So far, the following two (equivalent) properties have been introduced:
1. The number e is the unique positive real number such that
2. The number e is the unique positive real number such that
The following three characterizations can be proven equivalent:
3. The number e is the limit
Similarly:
4. The number e is the sum of the infinite series
where n! is the factorial of n.
5. The number e is the unique positive real number such that
Properties[edit]
Calculus[edit]
As in the motivation, the exponential function ex is important in part because it is the unique nontrivial function (up to multiplication by a constant) which is its own derivative
and therefore its own antiderivative as well:
Exponential-like functions[edit]

The global maximum for the function
occurs at x = e. Similarly, x = 1/e is where the global minimum occurs for the function
defined for positive x. More generally, x = e−1/n is where the global minimum occurs for the function
for any n > 0. The infinite tetration
- or ∞
converges if and only if e−e ≤ x ≤ e1/e (or approximately between 0.0660 and 1.4447), due to a theorem of Leonhard Euler.
Number theory[edit]
The real number e is irrational. Euler proved this by showing that its simple continued fraction expansion is infinite.[13] (See also Fourier's proof that e is irrational.)
Furthermore, by the Lindemann–Weierstrass theorem, e is transcendental, meaning that it is not a solution of any non-constant polynomial equation with rational coefficients. It was the first number to be proved transcendental without having been specifically constructed for this purpose (compare with Liouville number); the proof was given by Charles Hermite in 1873.
It is conjectured that e is normal, meaning that when e is expressed in any base the possible digits in that base are uniformly distributed (occur with equal probability in any sequence of given length).
Complex numbers[edit]
The exponential function ex may be written as a Taylor series
Because this series keeps many important properties for ex even when x is complex, it is commonly used to extend the definition of ex to the complex numbers. This, with the Taylor series for sin and cos x, allows one to derive Euler's formula:
which holds for all x. The special case with x = π is Euler's identity:
from which it follows that, in the principal branch of the logarithm,
Furthermore, using the laws for exponentiation,
which is de Moivre's formula.
The expression
is sometimes referred to as cis(x).
Differential equations[edit]
The general function
is the solution to the differential equation:
Representations[edit]
The number e can be represented as a real number in a variety of ways: as an infinite series, an infinite product, a continued fraction, or a limit of a sequence. The chief among these representations, particularly in introductory calculus courses is the limit
given above, as well as the series
given by evaluating the above power series for ex at x = 1.
Less common is the continued fraction (sequence A003417 in the OEIS).
which written out looks like
Many other series, sequence, continued fraction, and infinite product representations of e have been developed.
Stochastic representations[edit]
In addition to exact analytical expressions for representation of e, there are stochastic techniques for estimating e. One such approach begins with an infinite sequence of independent random variables X1, X2, ..., drawn from the uniform distribution on [0, 1]. Let V be the least number n such that the sum of the first n samples exceeds 1:
Then the expected value of V is e: E(V) = e.[15][16]
Known digits[edit]
The number of known digits of e has increased dramatically during the last decades. This is due both to the increased performance of computers and to algorithmic improvements.[17][18]
| Date | Decimal digits | Computation performed by |
|---|---|---|
| 1748 | 23 | Leonhard Euler[19] |
| 1853 | 137 | William Shanks |
| 1871 | 205 | William Shanks |
| 1884 | 346 | J. Marcus Boorman |
| 1949 | 2,010 | John von Neumann (on the ENIAC) |
| 1961 | 100,265 | Daniel Shanks and John Wrench[20] |
| 1978 | 116,000 | Stephen Gary Wozniak (on the Apple II[21]) |
| 1994 April 1 | 1,000,000 | Robert Nemiroff & Jerry Bonnell [22] |
| 1999 November 21 | 1,250,000,000 | Xavier Gourdon [23] |
| 2000 July 16 | 3,221,225,472 | Colin Martin & Xavier Gourdon [24] |
| 2003 September 18 | 50,100,000,000 | Shigeru Kondo & Xavier Gourdon [25] |
| 2007 April 27 | 100,000,000,000 | Shigeru Kondo & Steve Pagliarulo [26] |
| 2009 May 6 | 200,000,000,000 | Shigeru Kondo & Steve Pagliarulo [26] |
| 2010 July 5 | 1,000,000,000,000 | Shigeru Kondo & Alexander J. Yee [27] |
In computer culture[edit]
In contemporary internet culture, individuals and organizations frequently pay homage to the number e.
For example, in the IPO filing for Google, in 2004, rather than a typical round-number amount of money, the company announced its intention to raise $2,718,281,828, which is e billion dollars to the nearest dollar. Google was also responsible for a billboard[28] that appeared in the heart of Silicon Valley, and later in Cambridge, Massachusetts; Seattle, Washington; and Austin, Texas. It read {first 10-digit prime found in consecutive digits of e}.com. Solving this problem and visiting the advertised web site (now defunct) led to an even more difficult problem to solve, which in turn led to Google Labs where the visitor was invited to submit a resume.[29] The first 10-digit prime in e is 7427466391, which starts as late as at the 99th digit.[30]
In another instance, the computer scientist Donald Knuth let the version numbers of his program Metafont approach e. The versions are 2, 2.7, 2.71, 2.718, and so forth. Similarly, the version numbers of his TeX program approach π.[31]
Notes[edit]
- ^ Oxford English Dictionary, 2nd ed.
- ^ Encyclopedic Dictionary of Mathematics 142.D
- ^ Jerrold E. Marsden, Alan Weinstein (1985). Calculus. Springer. ISBN 0-387-90974-5.
- ^ Sondow, Jonathan. "e". Wolfram Mathworld. Wolfram Research. Retrieved 10 May 2011.
- ^ Howard Whitley Eves (1969). An Introduction to the History of Mathematics. Holt, Rinehart & Winston. ISBN 0-03-029558-0.
- ^ a b O'Connor, J J; Robertson, E F. "The number e". MacTutor History of Mathematics.
- ^ Remmert, Reinhold (1991), Theory of Complex Functions, Springer-Verlag, p. 136, ISBN 0-387-97195-5
- ^ Euler, Meditatio in experimenta explosione tormentorum nuper instituta.
- ^ Grinstead, C.M. and Snell, J.L.Introduction to probability theory (published online under the GFDL), p. 85.
- ^ Knuth (1997) The Art of Computer Programming Volume I, Addison-Wesley, p. 183 ISBN 0-201-03801-3.
- ^ Kline, M. (1998) Calculus: An intuitive and physical approach, section 12.3 "The Derived Functions of Logarithmic Functions.", pp. 337 ff, Courier Dover Publications, 1998, ISBN 0-486-40453-6
- ^ This is the approach taken by Kline (1998).
- ^ Sandifer, Ed (Feb. 2006). "How Euler Did It: Who proved e is Irrational?" (PDF). MAA Online. Retrieved 2010-06-18.
{{cite web}}: Check date values in:|date=(help) - ^ Hofstadter, D. R., "Fluid Concepts and Creative Analogies: Computer Models of the Fundamental Mechanisms of Thought" Basic Books (1995) ISBN 0-7139-9155-0
- ^ Russell, K. G. (1991) Estimating the Value of e by Simulation The American Statistician, Vol. 45, No. 1. (Feb., 1991), pp. 66–68.
- ^ Dinov, ID (2007) Estimating e using SOCR simulation, SOCR Hands-on Activities (retrieved December 26, 2007).
- ^ Sebah, P. and Gourdon, X.; The constant e and its computation
- ^ Gourdon, X.; Reported large computations with PiFast
- ^ Introductio in analysin infinitorum p. 90
- ^ Daniel Shanks and John W Wrench (1962). "Calculation of Pi to 100,000 Decimals" (PDF). Mathematics of Computation. 16 (77): 76–99 (78).
We have computed e on a 7090 to 100,265D by the obvious program
- ^ Byte Magazine Vol 6, Issue 6 (June 1981) p.392) "The Impossible Dream: Computing e to 116,000 places with a Personal Computer"
- ^ Email from Robert Nemiroff and Jerry Bonnell – The Number e to 1 Million Digits. None. Retrieved on 2012-02-24.
- ^ Email from Xavier Gourdon to Simon Plouffe – I have made a new e computation (with verification) : 1,250,000,000 digits. None. Retrieved on 2012-02-24.
- ^ PiHacks message 177 – E to 3,221,225,472 D. Groups.yahoo.com. Retrieved on 2012-02-24.
- ^ PiHacks message 1071 – Two new records : 50 billions for E and 25 billions for pi. Groups.yahoo.com. Retrieved on 2012-02-24.
- ^ a b English Version of PI WORLD. Ja0hxv.calico.jp. Retrieved on 2012-02-24.
- ^ A list of notable large computations of e. Numberworld.org. Retrieved on 2012-02-24.
- ^ First 10-digit prime found in consecutive digits of e}. Brain Tags. Retrieved on 2012-02-24.
- ^ Shea, Andrea. "Google Entices Job-Searchers with Math Puzzle". NPR. Retrieved 2007-06-09.
- ^ Kazmierczak, Marcus (2004-07-29). "Math : Google Labs Problems". mkaz.com. Retrieved 2007-06-09.
- ^ Knuth, Donald, "The Future of TeX and Metafont", TeX Mag, 5 (1)
Further reading[edit]
- Maor, Eli; e: The Story of a Number, ISBN 0-691-05854-7
- Commentary on Endnote 10 of the book Prime Obsession for another stochastic representation
External links[edit]
- An Intuitive Guide To Exponential Functions &e for the non-mathematician
- The number e to 1 million places and 2 and 5 million places
- e Approximations – Wolfram MathWorld
- Earliest Uses of Symbols for Constants
- "The story of e", by Robin Wilson at Gresham College, 28 February 2007 (available for audio and video download)
- e Search Engine 2 billion searchable digits of e, π and √2








![{\displaystyle e=\lim _{n\to \infty }{\frac {n}{\sqrt[{n}]{n!}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/310afedad5e855a28eb0d1b232a29031bd682548)










![{\displaystyle {\begin{aligned}e^{x}&=\int _{-\infty }^{x}e^{t}\,dt\\[8pt]&=\int _{-\infty }^{0}e^{t}\,dt+\int _{0}^{x}e^{t}\,dt\\[8pt]&=1+\int _{0}^{x}e^{t}\,dt.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/946f1ea90686802e25ec4cfee5032a5063f61b02)
![{\displaystyle {\sqrt[{x}]{x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61b4a0a76158849854a302fc639dfc882ec16008)
![{\displaystyle f(x)={\sqrt[{x}]{x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e15600c8e263f973cca6db5347531ea5a6846aa8)














![{\displaystyle e=\lim _{n\to \infty }[2;1,\mathbf {2} ,1,1,\mathbf {4} ,1,1,\mathbf {6} ,1,1,\mathbf {8} ,1,1,...,\mathbf {2n} ,1,1]=[1;\mathbf {0} ,1,1,\mathbf {2} ,1,1,\mathbf {4} ,1,1,...]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75ce6cc737eca1834e401011278c3421ff7bad57)

