Wikipedia:Reference desk/Archives/Mathematics/2009 November 24
| Mathematics desk | ||
|---|---|---|
| < November 23 | << Oct | November | Dec >> | November 25 > |
| Welcome to the Wikipedia Mathematics Reference Desk Archives |
|---|
| The page you are currently viewing is an archive page. While you can leave answers for any questions shown below, please ask new questions on one of the current reference desk pages. |
November 24
[edit]why does anyone bother with axioms since Goedel?
[edit]Ever since Goedel proved that the truth about a system will be a superset of the things you can show with your self-consistent axioms, why would anyone bother trying to start from a set of axioms and work their way through rigorously? Doesn't this reflect that they are less interested in the whole truth than in the part of it they can prove? Wouldn't it be akin to sweeping only around streetlamps (where the lit section is that part of the truth about your system which your axioms can prove), and leaving the rest of the street (the other true statements) untouched? For me, this behavior borders on a wanton disregard for discovering the whole truth (cleaning the whole pavement), and I don't understand why anyone bothers with axioms since Goedel. Any enlightenment would be appreciated. 92.230.68.236 (talk) 15:54, 24 November 2009 (UTC)
- What is the alternative? Give up on maths altogether? You can't prove anything without some premises and proof is what maths is all about. --Tango (talk) 15:57, 24 November 2009 (UTC)
| “ |
|
” |
- Math is not, strictly, a science, or at least not a natural science. Strict proof is a concept that is quite foreign to all empirical sciences. Your quest for "the whole truth" is unattainable (as shown by Goedel), so we stick to what we can show. And we can, of course, step outside any given system and use reasoning on a meta-level to show things that are unprovable in the original system. Of course our meta-system will have the same basic shortcoming. But what if we are not interested in "truth", but in "provable truth"? What we can prove has a chance to be useful - because it is provable. I'd rather have my bridge design checked by (incomplete) analysis that by (complete) voodoo. --Stephan Schulz (talk) 16:44, 24 November 2009 (UTC)
- Thanks, let me ask for a clarification on your word "unattainable". If the task is to find out which of 10 normal-looking coins is heavily weighted on one side only by flipping them (as many times as you want), would you call the truth in this situation "unattainable" in the same sense you just used? I mean, you can become more and more confident of it, but your conjecture will never become a rigorous proof. 92.230.68.236 (talk) 16:57, 24 November 2009 (UTC)
- Math is not, strictly, a science, or at least not a natural science. Strict proof is a concept that is quite foreign to all empirical sciences. Your quest for "the whole truth" is unattainable (as shown by Goedel), so we stick to what we can show. And we can, of course, step outside any given system and use reasoning on a meta-level to show things that are unprovable in the original system. Of course our meta-system will have the same basic shortcoming. But what if we are not interested in "truth", but in "provable truth"? What we can prove has a chance to be useful - because it is provable. I'd rather have my bridge design checked by (incomplete) analysis that by (complete) voodoo. --Stephan Schulz (talk) 16:44, 24 November 2009 (UTC)
- Well, your confidence is bounded not by certainty, but by certainty within your model of reality. What if there is an invisible demon who always flips one coin to head? What if you're living in the Matrix and the coins are just simulations? No matter what tools you are allowed to use, or how many witnesses there are, you cannot make statements about "the real world" with absolute certainty. This is a fundamental divide that separates math from the empirical sciences. --Stephan Schulz (talk) 17:41, 24 November 2009 (UTC)
- To my mind it wasn't Goedel who so much as Russell's paradox that shook up mathematics. It didn't say math might be inconsistent but that math, as understood at the time, was inconsistent. I have visions of accounting firms going on holiday until it was resolved because no one could be sure that sums would still add up the same from one day to the next.--RDBury (talk) 16:30, 24 November 2009 (UTC)
- You might be interested in Experimental mathematics. There is also quite a bit of maths where people have shown under fairly straightforward conditions that something is probably true. Riemann's hypothesis is an interesting case where people aren't even sure if it is true and yet there are many theorems which are proven only if it is true. Another interesting case is the Continuum hypothesis where people have been debating whether there are axioms which would be generally accepted which make it true or false. So basically mathematicians do look at things they can't or haven't been able to prove but they consider them unsatisfactory until a proof is available. Dmcq (talk) 17:10, 24 November 2009 (UTC)
- Thank you. Is it fair to say that Tango and S. Schulz above would probably say experimental mathematics isn't in some sense "real" mathematics? 92.230.68.236 (talk) —Preceding undated comment added 17:28, 24 November 2009 (UTC).
- Experimental maths is part of maths, but you haven't really finished until you have proven your result (or proven it can't be proven). Empirical evidence helps you work out what to try and prove, but it isn't enough on its own. --Tango (talk) 17:51, 24 November 2009 (UTC)
- I don't understand in what way experimental mathematics as described in that article shows that something is probably true. How does one quantify the probability? It looks to me like just plain numerically-based conjectures, an ancient part of mathematics. 67.117.145.149 (talk) 21:21, 24 November 2009 (UTC)
- If your conjecture about the natural numbers, say, is satisfied for the first billion natural numbers then that suggests it is probably true for all of them. I'm not sure you can quantify that, though - you would need a figure for the prior probability of it being true before you started experimenting, and I don't know where you would get such a figure. --Tango (talk) 23:52, 24 November 2009 (UTC)
- I don't understand in what way experimental mathematics as described in that article shows that something is probably true. How does one quantify the probability? It looks to me like just plain numerically-based conjectures, an ancient part of mathematics. 67.117.145.149 (talk) 21:21, 24 November 2009 (UTC)
- Experimental maths is part of maths, but you haven't really finished until you have proven your result (or proven it can't be proven). Empirical evidence helps you work out what to try and prove, but it isn't enough on its own. --Tango (talk) 17:51, 24 November 2009 (UTC)
- Thank you. Is it fair to say that Tango and S. Schulz above would probably say experimental mathematics isn't in some sense "real" mathematics? 92.230.68.236 (talk) —Preceding undated comment added 17:28, 24 November 2009 (UTC).
- I think when working with mathematics that the general experience is that most questions that mathematians are interested in can be decided by either proving or disproving them. So even though there exist propositions that can neither be proven or disproven, they seem seldomly to come up in practise. Of course we don't know if this impression will change in the future. Aenar (talk) 17:57, 24 November 2009 (UTC)
- I have the same impression. Is it fair to say that a mathematician thinks it's better to "decide" (prove or disprove) one unproven proposition than become very confident statistically in ten different ones whose true-value had been unknown? Maybe I'm just ignorant and the latter doesn't really happen in practice (by stark contrast with every other science) - is that it? 92.230.68.236 (talk) 18:10, 24 November 2009 (UTC)
- I wouldn't say that to "decide" is the same as prove (or disprove). I decided to have toast for breakfast this morning. Mathematicians discover and then prove. Mathematicians would rather prove something, but it isn't unknown for them to assume something that is very probably true as being true; take the Riemann hypothesis or Goldbach's conjecture for example. There are many results based on these propositions indeed being true. Although, to be honest, this doesn't sit very well with me. It seems to be too much like a house of cards for my liking. The beauty of mathematics is its truth and certainty. The problem with "the other sciences" is that you could conduct an experiment 1,000 times and get one result, and then on the 1,001st time get a different result: nothing is certain. ~~ Dr Dec (Talk) ~~ 18:31, 24 November 2009 (UTC)
- I might have used the word "decide" incorrectly; English is not my mother tongue. I used it (approximately) in the same way as in the article Decision problem. Aenar (talk) 22:48, 24 November 2009 (UTC)
- Indeed. There is a big difference between being 99.9999999999% sure that the next apple to fall from the tree in my garden will fall down, rather than up, and being 100% sure that the square of the hypotenuse of a right angled triangle is equal to the sum of the squares of the other two sides. The difference is precisely the difference between science and maths. --Tango (talk) 18:48, 24 November 2009 (UTC)
- I wouldn't say that to "decide" is the same as prove (or disprove). I decided to have toast for breakfast this morning. Mathematicians discover and then prove. Mathematicians would rather prove something, but it isn't unknown for them to assume something that is very probably true as being true; take the Riemann hypothesis or Goldbach's conjecture for example. There are many results based on these propositions indeed being true. Although, to be honest, this doesn't sit very well with me. It seems to be too much like a house of cards for my liking. The beauty of mathematics is its truth and certainty. The problem with "the other sciences" is that you could conduct an experiment 1,000 times and get one result, and then on the 1,001st time get a different result: nothing is certain. ~~ Dr Dec (Talk) ~~ 18:31, 24 November 2009 (UTC)
- I don't know. (My first impulse would be that that is not fair to say.) I believe in many cases it might actually be very hard to find a way to apply techniques of experimental mathematics. An example would be if one is trying to prove the existence of an abstract mathematical object which has certain properties. Aenar (talk) 18:38, 24 November 2009 (UTC)
- Experiments are fine, but you cannot usually generalize usefully from them in maths. For any arbitrarily large finite set of test values from, say, the natural numbers, I can give you a property that is 100% true on the test values, but whose overall probability to be true is zero (one such property is "P(x) iff x<= m, where m is the largest of your test values). --Stephan Schulz (talk) 18:44, 24 November 2009 (UTC)
- To clarify my example which was probably unclear: I was thinking of the object as being (for example) a topological space or another topological/geometric object, where there's no way to enumerate the possible candidate objects.
Besides that, I agree with Stephan Schulz.Actually, I'm not sure what I think. Aenar (talk) 18:53, 24 November 2009 (UTC)
- To clarify my example which was probably unclear: I was thinking of the object as being (for example) a topological space or another topological/geometric object, where there's no way to enumerate the possible candidate objects.
- In some fields experiments can be very useful (number theory, for example). In others, they are largely useless. --Tango (talk) 18:48, 24 November 2009 (UTC)
- Experiments are fine, but you cannot usually generalize usefully from them in maths. For any arbitrarily large finite set of test values from, say, the natural numbers, I can give you a property that is 100% true on the test values, but whose overall probability to be true is zero (one such property is "P(x) iff x<= m, where m is the largest of your test values). --Stephan Schulz (talk) 18:44, 24 November 2009 (UTC)
- I don't think mathematics has ever been about "the whole truth" or even "the part of it that they can prove". It's about the part that's meaningful and satisfying, which most of the time turns out to be provable. Very complex true statements (as shown by Chaitin and so forth) are usually unprovable but also tend to be too complicated for our tiny minds to ascribe meaning to. The statements applicable to traditional science (physics, etc.) turns out (according to Solomon Feferman) to mostly be provable in elementary number theory (Peano arithmetic).[1] You might like a couple of his other papers including "Does mathematics need new axioms?". 67.117.145.149 (talk) 21:38, 24 November 2009 (UTC)
- In my view mathematics is an experimental science; the differences from the physical sciences are largely ones of degree (and subject matter). It's true that there is a very old tradition of Euclidean foundationalism according to which mathematics is restricted to statements provable from axioms, but this is ultimately unsatisfactory because it does not give an account of why we choose one set of axioms over another. An extreme mathematical formalist view holds that the axioms are essentially arbitrary, but this, frankly, is nonsense on its face.
- A more effective way to think of mathematical statements (more effective in the sense that you'll get more and more useful results) is that they describe the behavior of genuine objects, naturals and reals and sets and so on, and that we want axioms that say true things about those objects, rather than false things. Beyond the simplest statements, which axioms are true as opposed to false is not always self-evident or immediately accessible to the intuition, and therefore the investigation gains an empirical component.
- For one example, Gottlob Frege's formalized version of set theory (Will Bailey says Frege didn't talk about sets per se; I have to look into that) was on its face not an unreasonable hypothesis, but it was utterly refuted by Russell's paradox. The modern conception of set theory, based on the von Neumann hierarchy, has not been refuted. This is an empirical difference.
- Continuing along these lines, perhaps the most clearly empirical investigation into mathematical axiomatics since the 1930s has been the program of large cardinal hypotheses. The empirical confirmation/disconfirmation of these is not purely restricted to finding contradictions (though a couple of these hypotheses have been refuted in this way); there is also the intricate interplay between large cardinals and levels of determinacy and regularity properties of sets of reals.
- Peter Koellner has written a truly excellent paper called On the Question of Absolute Undecidability, which I won't link in case there are any copyright issues but which you can find in five seconds through Google. I cannot recommend this paper enough for anyone interested in these questions; in addition to its other merits it has a great summary of these developments in the 20th century. --Trovatore (talk) 22:11, 24 November 2009 (UTC)
- As regards the original question: Rather than "why do we sweep only around the streetlights?" I think a better analogy might be "why do we drive cars, when they can't go on water?". It's certainly true that, whatever the currently accepted axioms might be, there will be things we'd like to know that those axioms can't tell us. But there are also things we'd like to know that we can deduce from the axioms. Should we say that, because we can't do everything, we should therefore do nothing?
- You might ask, OK, but you (Mike) say that we have ways of investigating the truth of statements that are not decided by a given set of axioms. Why not use those methods directly on whatever new question whose truth we'd like to know?
- The reason is that such investigations are much more difficult, and their outcomes much more arguable, than deduction from established axioms. And moreover, deductive reasoning is a major part of these investigations, so you're not going to get rid of it.
- The 100% certainty Tango claims is an illusion and always has been. Nevertheless, once in possession of a proof, we can circumscribe the kinds of error that are possible: The only way the statement can fail to be true is if there is an error in the axioms, or an error in the proof. An error in the axioms is always possible, but the axioms are not that many, and they have a lot of eyes on them; their justifications can be discussed in very fine detail. An error in the proof is also possible, but if any intermediate conclusion looks suspect, it is possible to break down that part of the proof into smaller pieces until an agreement can be reached as to whether it is sound. These things do not have to be perfect in order to be useful. --Trovatore (talk) 23:31, 24 November 2009 (UTC)
- "Error in the axioms" arguably makes no sense. They may fail to model your common-sense idea, but they are correct by definition. Formally, a theorem is always of the form Ax -> C, where Ax are the axioms, and C is the conjecture. Pythagoras' theorem, for example, implicitly assumes the axioms of planar trigonometry - it's wrong on a sphere. --Stephan Schulz (talk) 09:48, 25 November 2009 (UTC)
- But if we're interested in more than "formally" (which we are), then axioms can most definitely be wrong. You can formally stipulate an axiom 1+1=3, but it is wrong in the sense that it does not correctly describe the behavior of the underlying Platonic objects 1, 3, and plus. Of course you can give the symbols 1, 3, and +, different interpretations in some structure, but in the context we're discussing here, there is only one correct structure to interpret the symbols in. --Trovatore (talk) 10:00, 25 November 2009 (UTC)
- What is that one correct structure? Taemyr (talk) 10:10, 25 November 2009 (UTC)
- The natural numbers, of course. --Trovatore (talk) 10:16, 25 November 2009 (UTC)
- What about useful structures like N5 (or N256 or N232), which interpret the same symbols differently? --Stephan Schulz (talk) 10:53, 25 November 2009 (UTC)
- If you mean , you have to say so. Many languages have a default interpretation. Admittedly in this case we could have been interpreting the symbols in, say, the integers, rather than the naturals, which while it would have agreed on the outcome would have been strictly speaking a different interpretation.
- But all of this is a quibble; of course languages can be given different interpretations. The point is that when we have a well-specified intended interpretation, which we normally do, then it is not the axioms that define the truth of the propositions. Rather, the axioms must conform to the behavior of the intended interpretation. If they don't, they're wrong. --Trovatore (talk) 17:50, 25 November 2009 (UTC)
- What about useful structures like N5 (or N256 or N232), which interpret the same symbols differently? --Stephan Schulz (talk) 10:53, 25 November 2009 (UTC)
- The natural numbers, of course. --Trovatore (talk) 10:16, 25 November 2009 (UTC)
- What is that one correct structure? Taemyr (talk) 10:10, 25 November 2009 (UTC)
- But if we're interested in more than "formally" (which we are), then axioms can most definitely be wrong. You can formally stipulate an axiom 1+1=3, but it is wrong in the sense that it does not correctly describe the behavior of the underlying Platonic objects 1, 3, and plus. Of course you can give the symbols 1, 3, and +, different interpretations in some structure, but in the context we're discussing here, there is only one correct structure to interpret the symbols in. --Trovatore (talk) 10:00, 25 November 2009 (UTC)
- "Error in the axioms" arguably makes no sense. They may fail to model your common-sense idea, but they are correct by definition. Formally, a theorem is always of the form Ax -> C, where Ax are the axioms, and C is the conjecture. Pythagoras' theorem, for example, implicitly assumes the axioms of planar trigonometry - it's wrong on a sphere. --Stephan Schulz (talk) 09:48, 25 November 2009 (UTC)
What is exactly Sine, Cosine, and Tangent.
[edit]I understand how to use Sine, Cosine, and Tangent but I don't understand what they are. Like when I type in sin(2) in the calcuator, what is the calculator doing to it? How does it arrive at this? —Preceding unsigned comment added by 71.112.219.219 (talk) 18:48, 24 November 2009 (UTC)
- The exact values of sin(x), cos(x) and tan(x) are given by the ratios of the lengths of the sides of a right-angled triangle. See this section of the right-angled triangle article for the definitions. As for the calculator, well it could be using Taylor series to work out the value of sin(x). Certain nice values of x have simple answers, e.g. sin(0) = 0, sin(π/4) = 1/√2, sin(π/2) = 1, etc. If you asked your calculator to work out sin(x0) then it might find and the closest nice value and then substitute your x into the Taylor series of sine, expanded about the nice value. The reason for changing the expansion point is that the Taylor series converges to sin(x0) faster when the expansion point is closer to x0.
- (ec - with Tango's comment below) As an example, let's choose sin(0.1). Well 0.1 is very close to 0. So we expand sin(x) as a Taylor series about x = 0:
- So sin(0.1) ≈ 0.1 − 0.001/6 + 0.00001/120 − 0.0000001/5040 + …. Now, these terms get very small, very quickly. For example, the last term is roughly 1.98×10−11; so without any effort we have a value accurate to many decimal places. Since n! gets very large, very quickly, we don't need to add many terms before we can an answer accurate to many decimal places. So your calculator could use a bit of addition, subtraction, multiplication and division. ~~ Dr Dec (Talk) ~~ 19:03, 24 November 2009 (UTC)
- I'm not sure there is a need to find a good starting point. You'll get enough accurate digits after 5 or 6 terms for any (and any other x can be calculated by taking it modulo pi), and it doesn't take long to calculate 5 or 6 terms. --Tango (talk) 19:14, 24 November 2009 (UTC)
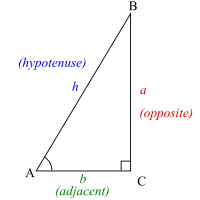
- (ec) There are various definitions, but most simply they are ratios of lengths of sides of right-angled triangles. sin(2) is the ratio of the opposite and the hypotenuse of a right-angled triangle with an angle of 2 units (either degrees or radians). Your calculator probably calculates it using a series, such as the Taylor series for sine, which is:
- The more terms you calculate, the more accurate an answer you get, so the calculator will calculate enough terms that all the digits it can fit on its screen are accurate. Alternatively, it might have a table of all the values stored in its memory, but I think the series method is more likely for trig functions. --Tango (talk) 19:09, 24 November 2009 (UTC)
These illustrations from the article titled trigonometric functions are probably better suited to answer this questions than are the ones in the right-triangle article:


Michael Hardy (talk) 04:08, 25 November 2009 (UTC)
- I think it's more likely that the calculator will use the CORDIC algorithm to calculate the values of trig (and other) functions. AndrewWTaylor (talk) 18:19, 25 November 2009 (UTC)
- Are you sure? By the looks of the article the method looks a lot more complicated then evaluating a polynomial. ~~ Dr Dec (Talk) ~~ 23:39, 25 November 2009 (UTC)
- Evaluating a polynomial is much harder if the chip does not have a hardware multiplier (which used to be, and maybe still is for all I know, fairly typical for pocket calculators). — Emil J. 11:27, 26 November 2009 (UTC)
- Are you sure? By the looks of the article the method looks a lot more complicated then evaluating a polynomial. ~~ Dr Dec (Talk) ~~ 23:39, 25 November 2009 (UTC)
Eponyms
[edit]Does anyone know after whom were the Dawson integral and the Bol loop named? Those two seem to be among the few wiki-articles on eponymous mathematical concepts, where there is no hint about their eponym. --Omnipaedista (talk) 22:00, 24 November 2009 (UTC)
- Bol loops were introduced in G. Bol's 1937 paper "Gewebe und Gruppen" in the Mathematische Annalen, volume 11, with reviews and e-prints at: Zbl 0016.22603 JFM 63.1157.04 MR1513147 doi:10.1007/BF01594185. de:Gerrit Bol has a biography with sources. His students are listed on the page for Gerrit Bol at the Mathematics Genealogy Project. JackSchmidt (talk) 22:22, 24 November 2009 (UTC)
- Thanks for the detailed answer. I suspected it was Gerrit Door Bol but I couldn't find the title of the original paper or any related information in order to verify it. As for Dawson's integral, it'd be great if someone knowledgeable on the literature of mathematical analysis could indicate where it appeared for the first time or at least Dawson's full name. --Omnipaedista (talk) 22:38, 24 November 2009 (UTC)
- Good question! I wasn't able to find a specific reference but my current theory is that it is John M. Dawson.
- This article gives a couple of references for the Dawson integral, the earlier of which is:
- [Stix, 1962] T. H. Stix, “The Theory of Plasma Waves”, McGraw-Hill Book Company, New York, 1962.
- Thomas H. Stix (more info) was a part of Project Matterhorn (now Princeton Plasma Physics Laboratory) from around 1953 to around 1961. In 1962 he was appointed as a professor at Princeton and wrote the above book.
- This article references both Stix's book and an article by a J.M. Dawson. That article is:
- Dawson, J. M., "Plasma Particle Accelerators," Scientific American, 260, 54, 1989.
- That paper appears on the selected recent publications list of John M. Dawson. Dawson earned his Ph.D in 1957, and was a part of Project Matterhorn from 1956 to 1962. His top research interest is listed as Numerical Modeling of Plasma. -- KathrynLybarger (talk) 01:38, 25 November 2009 (UTC)



![{\displaystyle x\in [-\pi ,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb1d5b7c7f8c8190cb14884785f2aa663f27feff)
