Jump to content

Geologic modelling

From Wikipedia, the free encyclopedia
(Redirected from Geomodelling)
Geological mapping software displaying a screenshot of a structure map generated for an 8500ft deep gas & Oil reservoir in the Earth field, Vermilion Parish, Erath, Louisiana. The left-to-right gap, near the top of the contour map indicates a Fault line. This fault line is between the blue/green contour lines and the purple/red/yellow contour lines. The thin red circular contour line in the middle of the map indicates the top of the oil reservoir. Because gas floats above oil, the thin red contour line marks the gas/oil contact zone.

Geologic modelling, geological modelling or geomodelling is the applied science of creating computerized representations of portions of the Earth's crust based on geophysical and geological observations made on and below the Earth surface. A geomodel is the numerical equivalent of a three-dimensional geological map complemented by a description of physical quantities in the domain of interest.[1] Geomodelling is related to the concept of Shared Earth Model;[2] which is a multidisciplinary, interoperable and updatable knowledge base about the subsurface.

Geomodelling is commonly used for managing natural resources, identifying natural hazards, and quantifying geological processes, with main applications to oil and gas fields, groundwater aquifers and ore deposits. For example, in the oil and gas industry, realistic geologic models are required as input to reservoir simulator programs, which predict the behavior of the rocks under various hydrocarbon recovery scenarios. A reservoir can only be developed and produced once; therefore, making a mistake by selecting a site with poor conditions for development is tragic and wasteful. Using geological models and reservoir simulation allows reservoir engineers to identify which recovery options offer the safest and most economic, efficient, and effective development plan for a particular reservoir.

Geologic modelling is a relatively recent subdiscipline of geology which integrates structural geology, sedimentology, stratigraphy, paleoclimatology, and diagenesis;

In 2-dimensions (2D), a geologic formation or unit is represented by a polygon, which can be bounded by faults, unconformities or by its lateral extent, or crop. In geological models a geological unit is bounded by 3-dimensional (3D) triangulated or gridded surfaces. The equivalent to the mapped polygon is the fully enclosed geological unit, using a triangulated mesh. For the purpose of property or fluid modelling these volumes can be separated further into an array of cells, often referred to as voxels (volumetric elements). These 3D grids are the equivalent to 2D grids used to express properties of single surfaces.

Geomodelling generally involves the following steps:[3]

  1. Preliminary analysis of geological context of the domain of study.
  2. Interpretation of available data and observations as point sets or polygonal lines (e.g. "fault sticks" corresponding to faults on a vertical seismic section).
  3. Construction of a structural model describing the main rock boundaries (horizons, unconformities, intrusions, faults)[4]
  4. Definition of a three-dimensional mesh honoring the structural model to support volumetric representation of heterogeneity (see Geostatistics) and solving the Partial Differential Equations which govern physical processes in the subsurface (e.g. seismic wave propagation, fluid transport in porous media).

Geologic modelling components

[edit]

Structural framework

[edit]

Incorporating the spatial positions of the major formation boundaries, including the effects of faulting, folding, and erosion (unconformities). The major stratigraphic divisions are further subdivided into layers of cells with differing geometries with relation to the bounding surfaces (parallel to top, parallel to base, proportional). Maximum cell dimensions are dictated by the minimum sizes of the features to be resolved (everyday example: On a digital map of a city, the location of a city park might be adequately resolved by one big green pixel, but to define the locations of the basketball court, the baseball field, and the pool, much smaller pixels – higher resolution – need to be used).

Rock type

[edit]

Each cell in the model is assigned a rock type. In a coastal clastic environment, these might be beach sand, high water energy marine upper shoreface sand, intermediate water energy marine lower shoreface sand, and deeper low energy marine silt and shale. The distribution of these rock types within the model is controlled by several methods, including map boundary polygons, rock type probability maps, or statistically emplaced based on sufficiently closely spaced well data.

Reservoir quality

[edit]

Reservoir quality parameters almost always include porosity and permeability, but may include measures of clay content, cementation factors, and other factors that affect the storage and deliverability of fluids contained in the pores of those rocks. Geostatistical techniques are most often used to populate the cells with porosity and permeability values that are appropriate for the rock type of each cell.

Fluid saturation

[edit]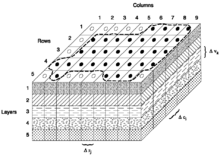
A 3D finite difference grid used in MODFLOW for simulating groundwater flow in an aquifer.

Most rock is completely saturated with groundwater. Sometimes, under the right conditions, some of the pore space in the rock is occupied by other liquids or gases. In the energy industry, oil and natural gas are the fluids most commonly being modelled. The preferred methods for calculating hydrocarbon saturations in a geologic model incorporate an estimate of pore throat size, the densities of the fluids, and the height of the cell above the water contact, since these factors exert the strongest influence on capillary action, which ultimately controls fluid saturations.

Geostatistics

[edit]

An important part of geologic modelling is related to geostatistics. In order to represent the observed data, often not on regular grids, we have to use certain interpolation techniques. The most widely used technique is kriging which uses the spatial correlation among data and intends to construct the interpolation via semi-variograms. To reproduce more realistic spatial variability and help assess spatial uncertainty between data, geostatistical simulation based on variograms, training images, or parametric geological objects is often used, e.g.[5]

Mineral Deposits

[edit]

Geologists involved in mining and mineral exploration use geologic modelling to determine the geometry and placement of mineral deposits in the subsurface of the earth. Geologic models help define the volume and concentration of minerals, to which economic constraints are applied to determine the economic value of the mineralization. Mineral deposits that are deemed to be economic may be developed into a mine.

Technology

[edit]

Geomodelling and CAD share a lot of common technologies. Software is usually implemented using object-oriented programming technologies in C++, Java or C# on one or multiple computer platforms. The graphical user interface generally consists of one or several 3D and 2D graphics windows to visualize spatial data, interpretations and modelling output. Such visualization is generally achieved by exploiting graphics hardware. User interaction is mostly performed through mouse and keyboard, although 3D pointing devices and immersive environments may be used in some specific cases. GIS (Geographic Information System) is also a widely used tool to manipulate geological data.

Geometric objects are represented with parametric curves and surfaces or discrete models such as polygonal meshes.[4][6]

Gravity Highs

Research in Geomodelling

[edit]

Problems pertaining to Geomodelling cover:[7][8]

  • Defining an appropriate Ontology to describe geological objects at various scales of interest,
  • Integrating diverse types of observations into 3D geomodels: geological mapping data, borehole data and interpretations, seismic images and interpretations, potential field data, well test data, etc.,
  • Better accounting for geological processes during model building,
  • Characterizing uncertainty about the geomodels to help assess risk. Therefore, Geomodelling has a close connection to Geostatistics and Inverse problem theory,
  • Applying of the recent developed Multiple Point Geostatistical Simulations (MPS) for integrating different data sources,[9]
  • Automated geometry optimization and topology conservation[10]

History

[edit]

In the 70's, geomodelling mainly consisted of automatic 2D cartographic techniques such as contouring, implemented as FORTRAN routines communicating directly with plotting hardware. The advent of workstations with 3D graphics capabilities during the 80's gave birth to a new generation of geomodelling software with graphical user interface which became mature during the 90's.[11][12][13]

Since its inception, geomodelling has been mainly motivated and supported by oil and gas industry.

Geologic modelling software

[edit]

Software developers have built several packages for geologic modelling purposes. Such software can display, edit, digitise and automatically calculate the parameters required by engineers, geologists and surveyors. Current software is mainly developed and commercialized by oil and gas or mining industry software vendors:

Geologic modelling and visualisation
Groundwater modelling
  • ZOOMQ3D

Moreover, industry Consortia or companies are specifically working at improving standardization and interoperability of earth science databases and geomodelling software:

  • Standardization: GeoSciML by the Commission for the Management and Application of Geoscience Information, of the International Union of Geological Sciences.
  • Standardization: RESQML(tm) by Energistics
  • Interoperability: OpenSpirit, by TIBCO(r)

See also

[edit]

References

[edit]

Footnotes

[edit]
  1. ^ Mallet, J. L. (2008). Numerical Earth Models. European Association of Geoscientists and Engineers (EAGE Publications bv). ISBN 978-90-73781-63-4. Archived from the original on 2016-03-04. Retrieved 2013-08-20.
  2. ^ Fanchi, John R. (August 2002). Shared Earth Modeling : Methodologies for Integrated Reservoir Simulations. Gulf Professional Publishing (Elsevier imprint). pp. xi–306. ISBN 978-0-7506-7522-2.
  3. ^ Chen, Shang-Ying; Hsieh, Bieng-Zih; Hsu, Kuo-Chin; Chang, Yi-Fei; Liu, Jia-Wei; Fan, Kai-Chun; Chiang, Li-Wei; Han, Yin-Lung (January 2021). "Well spacing of the doublet at the Huangtsuishan geothermal site, Taiwan". Geothermics. 89: 101968. Bibcode:2021Geoth..8901968C. doi:10.1016/j.geothermics.2020.101968. S2CID 224972986.
  4. ^ a b Caumon, G., Collon-Drouaillet, P., Le Carlier de Veslud, C., Sausse, J. and Viseur, S. (2009), Surface-based 3D modeling of geological structures, Mathematical Geosciences, 41(9):927–945
  5. ^ Cardenas, IC (2023). "A two-dimensional approach to quantify stratigraphic uncertainty from borehole data using non-homogeneous random fields". Engineering Geology. 314: 107001. Bibcode:2023EngGe.31407001C. doi:10.1016/j.enggeo.2023.107001. S2CID 255634245.
  6. ^ Mallet, J.-L., Geomodeling, Applied Geostatistics Series. Oxford University Press. ISBN 978-0-19-514460-4
  7. ^ Caumon, G., Towards stochastic time-varying geological modeling (2010), Mathematical Geosciences, 42(5):(555-569)
  8. ^ Perrin, M., Zhu, B., Rainaud, J.F. and Schneider, S. (2005), Knowledge-driven applications for geological modeling, "Journal of Petroleum Science and Engineering", 47(1–2):89–104
  9. ^ Tahmasebi, P., Hezarkhani, A., Sahimi, M., 2012, Multiple-point geostatistical modeling based on the cross-correlation functions, Computational Geosciences, 16(3):779-79742
  10. ^ M.R. Alvers, H.J. Götze, B. Lahmeyer, C. Plonka and S. Schmidt, 2013, Advances in 3D Potential Field Modeling EarthDoc, 75th EAGE Conference & Exhibition incorporating SPE EUROPEC 2013
  11. ^ Dynamic Graphics History Archived 2011-07-25 at the Wayback Machine
  12. ^ Origin of the Gocad software
  13. ^ J. L. Mallet, P. Jacquemin, and N. Cheimanoff (1989). GOCAD project: Geometric modeling of complex geological surfaces, SEG Expanded Abstracts 8, 126, doi:10.1190/1.1889515
[edit]
Retrieved from "https://en.wikipedia.org/w/index.php?title=Geologic_modelling&oldid=1251679817"