Convergent series

"Convergent Series" redirects here. For the short story collection, see Convergent Series (short story collection).

In mathematics, a series is the sum of the terms of a sequence of numbers.

Given a sequence $\left \{ a_1,\ a_2,\ a_3,\dots \right \}$, the nth partial sum $S_n$ is the sum of the first n terms of the sequence, that is,

$S_n = \sum_{k=1}^n a_k.$

A series is convergent if the sequence of its partial sums $\left \{ S_1,\ S_2,\ S_3,\dots \right \}$ converges. In more formal language, a series converges if there exists a limit $\ell$ such that for any arbitrarily small positive number $\varepsilon > 0$, there is a large integer $N$ such that for all $n \ge \ N$,

$\left | S_n - \ell \right \vert \le \ \varepsilon.$

A series that is not convergent is said to be divergent.

Examples of convergent and divergent series

• The reciprocals of the positive integers produce a divergent series (harmonic series):

  ${1 \over 1}+{1 \over 2}+{1 \over 3}+{1 \over 4}+{1 \over 5}+{1 \over 6}+\cdots \rightarrow \infty.$

• Alternating the signs of the reciprocals of positive integers produces a convergent series:

  ${1\over 1} -{1\over 2} + {1\over 3} - {1\over 4} + {1\over 5} \cdots = \ln(2)$

• Alternating the signs of the reciprocals of positive odd integers produces a convergent series (the Leibniz formula for pi):

  ${1 \over 1}-{1 \over 3}+{1 \over 5}-{1 \over 7}+{1 \over 9}-{1 \over 11}+\cdots = {\pi \over 4}.$

• The reciprocals of prime numbers produce a divergent series (so the set of primes is "large"):

  ${1 \over 2}+{1 \over 3}+{1 \over 5}+{1 \over 7}+{1 \over 11}+{1 \over 13}+\cdots \rightarrow \infty.$

• The reciprocals of triangular numbers produce a convergent series:

  ${1 \over 1}+{1 \over 3}+{1 \over 6}+{1 \over 10}+{1 \over 15}+{1 \over 21}+\cdots = 2.$

• The reciprocals of factorials produce a convergent series (see e):

  $\frac{1}{1} + \frac{1}{1} + \frac{1}{2} + \frac{1}{6} + \frac{1}{24} + \frac{1}{120} + \cdots = e.$

• The reciprocals of square numbers produce a convergent series (the Basel problem):

  ${1 \over 1}+{1 \over 4}+{1 \over 9}+{1 \over 16}+{1 \over 25}+{1 \over 36}+\cdots = {\pi^2 \over 6}.$

• The reciprocals of powers of 2 produce a convergent series (so the set of powers of 2 is "small"):

  ${1 \over 1}+{1 \over 2}+{1 \over 4}+{1 \over 8}+{1 \over 16}+{1 \over 32}+\cdots = 2.$

• Alternating the signs of reciprocals of powers of 2 also produces a convergent series:

  ${1 \over 1}-{1 \over 2}+{1 \over 4}-{1 \over 8}+{1 \over 16}-{1 \over 32}+\cdots = {2\over3}.$

• The reciprocals of Fibonacci numbers produce a convergent series (see ψ):

  $\frac{1}{1} + \frac{1}{1} + \frac{1}{2} + \frac{1}{3} + \frac{1}{5} + \frac{1}{8} + \cdots = \psi.$

Convergence tests

Main article: Convergence tests

There are a number of methods of determining whether a series converges or diverges.

If the blue series, $\Sigma b_n$, can be proven to converge, then the smaller series, $\Sigma a_n$ must converge. By contraposition, if the red series, $\Sigma a_n$ is proven to diverge, then $\Sigma b_n$ must also diverge.

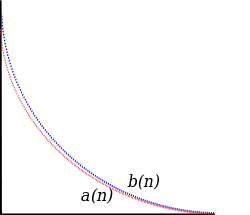
Comparison test. The terms of the sequence $\left \{ a_n \right \}$ are compared to those of another sequence $\left \{ b_n \right \}$. If,

for all n, $0 \le \ a_n \le \ b_n$, and $\sum_{n=1}^\infty b_n$ converges, then so does $\sum_{n=1}^\infty a_n.$

However, if,

for all n, $0 \le \ a_n \le \ b_n$, and $\sum_{n=1}^\infty a_n$ diverges, then so does $\sum_{n=1}^\infty b_n.$

Ratio test. Assume that for all n, $a_n > 0$. Suppose that there exists $r$ such that

$\lim_{n \to \infty} \frac{a_{n+1}}{a_n} = r.$

If r < 1, then the series converges. If r > 1, then the series diverges. If r = 1, the ratio test is inconclusive, and the series may converge or diverge.

Root test or nth root test. Suppose that the terms of the sequence in question are non-negative. Define r as follows:

$r = \limsup_{n\rightarrow\infty}\sqrt[n]{|a_n|},$

where "lim sup" denotes the limit superior (possibly ∞; if the limit exists it is the same value).

If r < 1, then the series converges. If r > 1, then the series diverges. If r = 1, the root test is inconclusive, and the series may converge or diverge.

The ratio test and the root test are both based on comparison with a geometric series, and as such they work in similar situations. In fact, if the ratio test works (meaning that the limit exists and is not equal to 1) then so does the root test; the converse, however, is not true. The root test is therefore more generally applicable, but as a practical matter the limit is often difficult to compute for commonly seen types of series.

Integral test. The series can be compared to an integral to establish convergence or divergence. Let $f(n) = a_n$ be a positive and monotone decreasing function. If

$\int_{1}^{\infty} f(x)\, dx = \lim_{t \to \infty} \int_{1}^{t} f(x)\, dx < \infty,$

then the series converges. But if the integral diverges, then the series does so as well.

Limit comparison test. If $\left \{ a_n \right \}, \left \{ b_n \right \} > 0$, and the limit $\lim_{n \to \infty} \frac{a_n}{b_n}$ exists and is not zero, then $\sum_{n=1}^\infty a_n$ converges if and only if $\sum_{n=1}^\infty b_n$ converges.

Alternating series test. Also known as the Leibniz criterion, the alternating series test states that for an alternating series of the form $\sum_{n=1}^\infty a_n (-1)^n$, if $\left \{ a_n \right \}$ is monotone decreasing, and has a limit of 0 at infinity, then the series converges.

Cauchy condensation test. If $\left \{ a_n \right \}$ is a positive monotone decreasing sequence, then $\sum_{n=1}^\infty a_n$ converges if and only if $\sum_{k=1}^\infty 2^k a_{2^{k}}$ converges.

Dirichlet's test

Abel's test

Raabe's test

Conditional and absolute convergence

Illustration of the absolute convergence of the power series of Exp[z] around 0 evaluated at z = Exp[ⁱ⁄₃]. The length of the line is finite.

Illustration of the conditional convergence of the power series of log(z+1) around 0 evaluated at z = exp((π−¹⁄₃)i). The length of the line is infinite.

For any sequence $\left \{ a_1,\ a_2,\ a_3,\dots \right \}$, $a_n \le \ \left | a_n \right \vert$ for all n. Therefore,

$\sum_{n=1}^\infty a_n \le \ \sum_{n=1}^\infty \left | a_n \right \vert.$

This means that if $\sum_{n=1}^\infty \left | a_n \right \vert$ converges, then $\sum_{n=1}^\infty a_n$ also converges (but not vice-versa).

If the series $\sum_{n=1}^\infty \left | a_n \right \vert$ converges, then the series $\sum_{n=1}^\infty a_n$ is absolutely convergent. An absolutely convergent sequence is one in which the length of the line created by joining together all of the increments to the partial sum is finitely long. The power series of the exponential function is absolutely convergent everywhere.

If the series $\sum_{n=1}^\infty a_n$ converges but the series $\sum_{n=1}^\infty \left | a_n \right \vert$ diverges, then the series $\sum_{n=1}^\infty a_n$ is conditionally convergent. The path formed by connecting the partial sums of a conditionally convergent series is infinitely long. The power series of the logarithm is conditionally convergent.

The Riemann series theorem states that if a series converges conditionally, it is possible to rearrange the terms of the series in such a way that the series converges to any value, or even diverges.

Uniform convergence

Main article: uniform convergence.

Let $\left \{ f_1,\ f_2,\ f_3,\dots \right \}$ be a sequence of functions. The series $\sum_{n=1}^\infty f_n$ is said to converge uniformly to f if the sequence $\{s_n\}$ of partial sums defined by

$s_n(x) = \sum_{k=1}^n f_k (x)$

converges uniformly to f.

There is an analogue of the comparison test for infinite series of functions called the Weierstrass M-test.

Cauchy convergence criterion

The Cauchy convergence criterion states that a series

$\sum_{n=1}^\infty a_n$

converges if and only if the sequence of partial sums is a Cauchy sequence. This means that for every $\varepsilon > 0,$ there is a positive integer $N$ such that for all $n \geq m \geq N$ we have

$\left| \sum_{k=m}^n a_k \right| < \varepsilon,$

which is equivalent to

$\lim_{n \to \infty \atop m\to \infty} \sum_{k=n}^{n+m} a_k = 0.$

See also

• Convergent sequence
• Normal convergence
• List of mathematical series
• Divergent series

External links

• Hazewinkel, Michiel, ed. (2001), "Series", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4 
• Weisstein, Eric (2005). Riemann Series Theorem. Retrieved May 16, 2005.