SHA-2
| Secure Hash Algorithms | |
|---|---|
| Concepts | |
| hash functions, SHA, DSA | |
| Main standards | |
| SHA-0, SHA-1, SHA-2, SHA-3 | |
| General | |
|---|---|
| Designers | National Security Agency |
| First published | 2001 |
| Series | (SHA-0), SHA-1, SHA-2, SHA-3 |
| Certification | FIPS PUB 180-4, CRYPTREC, NESSIE |
| Detail | |
| Digest sizes | 224, 256, 384, or 512 bits |
| Structure | Merkle–Damgård construction with Davies–Meyer compression function |
| Rounds | 64 or 80 |
| Best public cryptanalysis | |
| A 2011 attack breaks preimage resistance for 57 out of 80 rounds of SHA-512, and 52 out of 64 rounds for SHA-256.[1]
Pseudo-collision attack against up to 46 rounds of SHA-256.[2] SHA-256 and SHA-512 are prone to length extension attacks. By guessing the hidden part of the state, length extension attacks on SHA-224 and SHA-384 succeed with probability 2−(256−224) = 2−32 > 2−224 and 2−(512−384) = 2−128 > 2−384 respectively. | |
SHA-2 (Secure Hash Algorithm 2) is a set of cryptographic hash functions designed by the United States National Security Agency (NSA) and first published in 2001.[3][4] They are built using the Merkle–Damgård construction, from a one-way compression function itself built using the Davies–Meyer structure from a specialized block cipher.
SHA-2 includes significant changes from its predecessor, SHA-1. The SHA-2 family consists of six hash functions with digests (hash values) that are 224, 256, 384 or 512 bits:[5] SHA-224, SHA-256, SHA-384, SHA-512, SHA-512/224, SHA-512/256. SHA-256 and SHA-512 are novel hash functions computed with eight 32-bit and 64-bit words, respectively. They use different shift amounts and additive constants, but their structures are otherwise virtually identical, differing only in the number of rounds. SHA-224 and SHA-384 are truncated versions of SHA-256 and SHA-512 respectively, computed with different initial values. SHA-512/224 and SHA-512/256 are also truncated versions of SHA-512, but the initial values are generated using the method described in Federal Information Processing Standards (FIPS) PUB 180-4.
SHA-2 was first published by the National Institute of Standards and Technology (NIST) as a U.S. federal standard. The SHA-2 family of algorithms are patented in the U.S.[6] The United States has released the patent under a royalty-free license.[5]
As of 2011, the best public attacks break preimage resistance for 52 out of 64 rounds of SHA-256 or 57 out of 80 rounds of SHA-512, and collision resistance for 46 out of 64 rounds of SHA-256.[1][2]
Hash standard[edit]
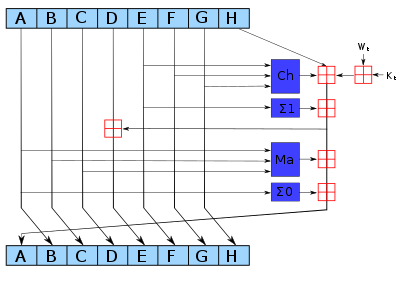
The bitwise rotation uses different constants for SHA-512. The given numbers are for SHA-256.
The red is addition modulo 232 for SHA-256, or 264 for SHA-512.
With the publication of FIPS PUB 180-2, NIST added three additional hash functions in the SHA family. The algorithms are collectively known as SHA-2, named after their digest lengths (in bits): SHA-256, SHA-384, and SHA-512.
The algorithms were first published in 2001 in the draft FIPS PUB 180-2, at which time public review and comments were accepted. In August 2002, FIPS PUB 180-2 became the new Secure Hash Standard, replacing FIPS PUB 180-1, which was released in April 1995. The updated standard included the original SHA-1 algorithm, with updated technical notation consistent with that describing the inner workings of the SHA-2 family.[4]
In February 2004, a change notice was published for FIPS PUB 180-2, specifying an additional variant, SHA-224, defined to match the key length of two-key Triple DES.[7] In October 2008, the standard was updated in FIPS PUB 180-3, including SHA-224 from the change notice, but otherwise making no fundamental changes to the standard. The primary motivation for updating the standard was relocating security information about the hash algorithms and recommendations for their use to Special Publications 800-107 and 800-57.[8][9][10] Detailed test data and example message digests were also removed from the standard, and provided as separate documents.[11]
In January 2011, NIST published SP800-131A, which specified a move from the then-current minimum of 80-bit security (provided by SHA-1) allowable for federal government use until the end of 2013, to 112-bit security (provided by SHA-2) being both the minimum requirement (starting in 2014) and the recommended security level (starting from the publication date in 2011).[12]
In March 2012, the standard was updated in FIPS PUB 180-4, adding the hash functions SHA-512/224 and SHA-512/256, and describing a method for generating initial values for truncated versions of SHA-512. Additionally, a restriction on padding the input data prior to hash calculation was removed, allowing hash data to be calculated simultaneously with content generation, such as a real-time video or audio feed. Padding the final data block must still occur prior to hash output.[13]
In July 2012, NIST revised SP800-57, which provides guidance for cryptographic key management. The publication disallowed creation of digital signatures with a hash security lower than 112 bits after 2013. The previous revision from 2007 specified the cutoff to be the end of 2010.[10] In August 2012, NIST revised SP800-107 in the same manner.[9]
The NIST hash function competition selected a new hash function, SHA-3, in 2012.[14] The SHA-3 algorithm is not derived from SHA-2.
Applications[edit]
The SHA-2 hash function is implemented in some widely used security applications and protocols, including TLS and SSL, PGP, SSH, S/MIME, and IPsec. The inherent computational demand of SHA-2 algorithms has driven the proposal of more efficient solutions, such as those based on application-specific integrated circuits (ASICs) hardware accelerators.[15]
SHA-256 is used for authenticating Debian software packages[16] and in the DKIM message signing standard; SHA-512 is part of a system to authenticate archival video from the International Criminal Tribunal of the Rwandan genocide.[17] SHA-256 and SHA-512 are proposed for use in DNSSEC.[18] Unix and Linux vendors are moving to using 256- and 512-bit SHA-2 for secure password hashing.[19]
Several cryptocurrencies, including Bitcoin, use SHA-256 for verifying transactions and calculating proof of work[20] or proof of stake.[21] The rise of ASIC SHA-2 accelerator chips has led to the use of scrypt-based proof-of-work schemes.
SHA-1 and SHA-2 are the Secure Hash Algorithms required by law for use in certain U.S. Government applications, including use within other cryptographic algorithms and protocols, for the protection of sensitive unclassified information. FIPS PUB 180-1 also encouraged adoption and use of SHA-1 by private and commercial organizations. SHA-1 is being retired for most government uses; the U.S. National Institute of Standards and Technology says, "Federal agencies should stop using SHA-1 for...applications that require collision resistance as soon as practical, and must use the SHA-2 family of hash functions for these applications after 2010" (emphasis in original).[22] NIST's directive that U.S. government agencies ought to, but not explicitly must, stop uses of SHA-1 after 2010[23] was hoped to accelerate migration away from SHA-1.
The SHA-2 functions were not quickly adopted initially, despite better security than SHA-1. Reasons might include lack of support for SHA-2 on systems running Windows XP SP2 or older[24] and a lack of perceived urgency since SHA-1 collisions had not yet been found. The Google Chrome team announced a plan to make their web browser gradually stop honoring SHA-1-dependent TLS certificates over a period from late 2014 and early 2015.[25][26][27] Similarly, Microsoft announced[28] that Internet Explorer and Edge would stop honoring public SHA-1-signed TLS certificates from February 2017. Mozilla disabled SHA-1 in early January 2016, but had to re-enable it temporarily via a Firefox update, after problems with web-based user interfaces of some router models and security appliances.[29]
Cryptanalysis and validation[edit]
For a hash function for which L is the number of bits in the message digest, finding a message that corresponds to a given message digest can always be done using a brute force search in 2L evaluations. This is called a preimage attack and may or may not be practical depending on L and the particular computing environment. The second criterion, finding two different messages that produce the same message digest, known as a collision, requires on average only 2L/2 evaluations using a birthday attack.
Some of the applications that use cryptographic hashes, such as password storage, are only minimally affected by a collision attack. Constructing a password that works for a given account requires a preimage attack, as well as access to the hash of the original password (typically in the shadow file) which may or may not be trivial. Reversing password encryption (e.g., to obtain a password to try against a user's account elsewhere) is not made possible by the attacks. (However, even a secure password hash cannot prevent brute-force attacks on weak passwords.)
In the case of document signing, an attacker could not simply fake a signature from an existing document—the attacker would have to produce a pair of documents, one innocuous and one damaging, and get the private key holder to sign the innocuous document. There are practical circumstances in which this is possible; until the end of 2008, it was possible to create forged SSL certificates using an MD5 collision which would be accepted by widely used web browsers.[30]
Increased interest in cryptographic hash analysis during the SHA-3 competition produced several new attacks on the SHA-2 family, the best of which are given in the table below. Only the collision attacks are of practical complexity; none of the attacks extend to the full round hash function.
At FSE 2012, researchers at Sony gave a presentation suggesting pseudo-collision attacks could be extended to 52 rounds on SHA-256 and 57 rounds on SHA-512 by building upon the biclique pseudo-preimage attack.[31]
| Published in | Year | Attack method | Attack | Variant | Rounds | Complexity |
|---|---|---|---|---|---|---|
| New Collision Attacks Against Up To 24-step SHA-2[32][33] | 2008 | Differential | Collision | SHA-256 | 24/64 | 215.5 |
| SHA-512 | 24/80 | 222.5 | ||||
| Preimages for step-reduced SHA-2[34] | 2009 | Meet-in-the-middle | Preimage | SHA-256 | 42/64 | 2251.7 |
| 43/64 | 2254.9 | |||||
| SHA-512 | 42/80 | 2502.3 | ||||
| 46/80 | 2511.5 | |||||
| Advanced meet-in-the-middle preimage attacks[35] | 2010 | Meet-in-the-middle | Preimage | SHA-256 | 42/64 | 2248.4 |
| SHA-512 | 42/80 | 2494.6 | ||||
| Higher-Order Differential Attack on Reduced SHA-256[2] | 2011 | Differential | Pseudo-collision | SHA-256 | 46/64 | 2178 |
| 33/64 | 246 | |||||
| Bicliques for Preimages: Attacks on Skein-512 and the SHA-2 family[1] | 2011 | Biclique | Preimage | SHA-256 | 45/64 | 2255.5 |
| SHA-512 | 50/80 | 2511.5 | ||||
| Pseudo-preimage | SHA-256 | 52/64 | 2255 | |||
| SHA-512 | 57/80 | 2511 | ||||
| Improving Local Collisions: New Attacks on Reduced SHA-256[36] | 2013 | Differential | Collision | SHA-256 | 31/64 | 265.5 |
| Pseudo-collision | SHA-256 | 38/64 | 237 | |||
| Branching Heuristics in Differential Collision Search with Applications to SHA-512[37] | 2014 | Heuristic differential | Pseudo-collision | SHA-512 | 38/80 | 240.5 |
| Analysis of SHA-512/224 and SHA-512/256[38] | 2016 | Differential | Collision | SHA-256 | 28/64 | practical |
| SHA-512 | 27/80 | practical | ||||
| Pseudo-collision | SHA-512 | 39/80 | practical | |||
| New Records in Collision Attacks on SHA-2[39] | 2023 | Differential | Collision | SHA-256 | 31/64 | 249.8 |
| SHA-512 | 31/80 | 2115.6 | ||||
| Pseudo-collision | SHA-256 | 39/64 | practical |
Official validation[edit]
Implementations of all FIPS-approved security functions can be officially validated through the CMVP program, jointly run by the National Institute of Standards and Technology (NIST) and the Communications Security Establishment (CSE). For informal verification, a package to generate a high number of test vectors is made available for download on the NIST site; the resulting verification, however, does not replace the formal CMVP validation, which is required by law[citation needed] for certain applications.
As of December 2013[update], there are over 1300 validated implementations of SHA-256 and over 900 of SHA-512, with only 5 of them being capable of handling messages with a length in bits not a multiple of eight while supporting both variants.[40]
Test vectors[edit]
Hash values of an empty string (i.e., a zero-length input text).
SHA224("") 0x d14a028c2a3a2bc9476102bb288234c415a2b01f828ea62ac5b3e42f SHA256("") 0x e3b0c44298fc1c149afbf4c8996fb92427ae41e4649b934ca495991b7852b855 SHA384("") 0x 38b060a751ac96384cd9327eb1b1e36a21fdb71114be07434c0cc7bf63f6e1da274edebfe76f65fbd51ad2f14898b95b SHA512("") 0x cf83e1357eefb8bdf1542850d66d8007d620e4050b5715dc83f4a921d36ce9ce47d0d13c5d85f2b0ff8318d2877eec2f63b931bd47417a81a538327af927da3e SHA512/224("") 0x 6ed0dd02806fa89e25de060c19d3ac86cabb87d6a0ddd05c333b84f4 SHA512/256("") 0x c672b8d1ef56ed28ab87c3622c5114069bdd3ad7b8f9737498d0c01ecef0967a
Even a small change in the message will (with overwhelming probability) result in a different hash, due to the avalanche effect. For example, adding a period to the end of the following sentence changes approximately half (111 out of 224) of the bits in the hash, equivalent to picking a new hash at random:
SHA224("The quick brown fox jumps over the lazy dog") 0x 730e109bd7a8a32b1cb9d9a09aa2325d2430587ddbc0c38bad911525 SHA224("The quick brown fox jumps over the lazy dog.") 0x 619cba8e8e05826e9b8c519c0a5c68f4fb653e8a3d8aa04bb2c8cd4c
Pseudocode[edit]
Pseudocode for the SHA-256 algorithm follows. Note the great increase in mixing between bits of the w[16..63] words compared to SHA-1.
Note 1: All variables are 32 bit unsigned integers and addition is calculated modulo 232 Note 2: For each round, there is one round constant k[i] and one entry in the message schedule array w[i], 0 ≤ i ≤ 63 Note 3: The compression function uses 8 working variables, a through h Note 4: Big-endian convention is used when expressing the constants in this pseudocode, and when parsing message block data from bytes to words, for example, the first word of the input message "abc" after padding is 0x61626380 Initialize hash values: (first 32 bits of the fractional parts of the square roots of the first 8 primes 2..19): h0 := 0x6a09e667 h1 := 0xbb67ae85 h2 := 0x3c6ef372 h3 := 0xa54ff53a h4 := 0x510e527f h5 := 0x9b05688c h6 := 0x1f83d9ab h7 := 0x5be0cd19 Initialize array of round constants: (first 32 bits of the fractional parts of the cube roots of the first 64 primes 2..311): k[0..63] := 0x428a2f98, 0x71374491, 0xb5c0fbcf, 0xe9b5dba5, 0x3956c25b, 0x59f111f1, 0x923f82a4, 0xab1c5ed5, 0xd807aa98, 0x12835b01, 0x243185be, 0x550c7dc3, 0x72be5d74, 0x80deb1fe, 0x9bdc06a7, 0xc19bf174, 0xe49b69c1, 0xefbe4786, 0x0fc19dc6, 0x240ca1cc, 0x2de92c6f, 0x4a7484aa, 0x5cb0a9dc, 0x76f988da, 0x983e5152, 0xa831c66d, 0xb00327c8, 0xbf597fc7, 0xc6e00bf3, 0xd5a79147, 0x06ca6351, 0x14292967, 0x27b70a85, 0x2e1b2138, 0x4d2c6dfc, 0x53380d13, 0x650a7354, 0x766a0abb, 0x81c2c92e, 0x92722c85, 0xa2bfe8a1, 0xa81a664b, 0xc24b8b70, 0xc76c51a3, 0xd192e819, 0xd6990624, 0xf40e3585, 0x106aa070, 0x19a4c116, 0x1e376c08, 0x2748774c, 0x34b0bcb5, 0x391c0cb3, 0x4ed8aa4a, 0x5b9cca4f, 0x682e6ff3, 0x748f82ee, 0x78a5636f, 0x84c87814, 0x8cc70208, 0x90befffa, 0xa4506ceb, 0xbef9a3f7, 0xc67178f2 Pre-processing (Padding): begin with the original message of length L bits append a single '1' bit append K '0' bits, where K is the minimum number >= 0 such that (L + 1 + K + 64) is a multiple of 512 append L as a 64-bit big-endian integer, making the total post-processed length a multiple of 512 bits such that the bits in the message are: <original message of length L> 1 <K zeros> <L as 64 bit integer> , (the number of bits will be a multiple of 512) Process the message in successive 512-bit chunks: break message into 512-bit chunks for each chunk create a 64-entry message schedule array w[0..63] of 32-bit words (The initial values in w[0..63] don't matter, so many implementations zero them here) copy chunk into first 16 words w[0..15] of the message schedule array Extend the first 16 words into the remaining 48 words w[16..63] of the message schedule array: for i from 16 to 63 s0 := (w[i-15] rightrotate 7) xor (w[i-15] rightrotate 18) xor (w[i-15] rightshift 3) s1 := (w[i-2] rightrotate 17) xor (w[i-2] rightrotate 19) xor (w[i-2] rightshift 10) w[i] := w[i-16] + s0 + w[i-7] + s1 Initialize working variables to current hash value: a := h0 b := h1 c := h2 d := h3 e := h4 f := h5 g := h6 h := h7 Compression function main loop: for i from 0 to 63 S1 := (e rightrotate 6) xor (e rightrotate 11) xor (e rightrotate 25) ch := (e and f) xor ((not e) and g) temp1 := h + S1 + ch + k[i] + w[i] S0 := (a rightrotate 2) xor (a rightrotate 13) xor (a rightrotate 22) maj := (a and b) xor (a and c) xor (b and c) temp2 := S0 + maj h := g g := f f := e e := d + temp1 d := c c := b b := a a := temp1 + temp2 Add the compressed chunk to the current hash value: h0 := h0 + a h1 := h1 + b h2 := h2 + c h3 := h3 + d h4 := h4 + e h5 := h5 + f h6 := h6 + g h7 := h7 + h Produce the final hash value (big-endian): digest := hash := h0 append h1 append h2 append h3 append h4 append h5 append h6 append h7
The computation of the ch and maj values can be optimized the same way as described for SHA-1.
SHA-224 is identical to SHA-256, except that:
- the initial hash values
h0throughh7are different, and - the output is constructed by omitting
h7.
SHA-224 initial hash values (in big endian): (The second 32 bits of the fractional parts of the square roots of the 9th through 16th primes 23..53) h[0..7] := 0xc1059ed8, 0x367cd507, 0x3070dd17, 0xf70e5939, 0xffc00b31, 0x68581511, 0x64f98fa7, 0xbefa4fa4
SHA-512 is identical in structure to SHA-256, but:
- the message is broken into 1024-bit chunks,
- the initial hash values and round constants are extended to 64 bits,
- there are 80 rounds instead of 64,
- the message schedule array w has 80 64-bit words instead of 64 32-bit words,
- to extend the message schedule array w, the loop is from 16 to 79 instead of from 16 to 63,
- the round constants are based on the first 80 primes 2..409,
- the word size used for calculations is 64 bits long,
- the appended length of the message (before pre-processing), in bits, is a 128-bit big-endian integer, and
- the shift and rotate amounts used are different.
SHA-512 initial hash values (in big-endian): h[0..7] := 0x6a09e667f3bcc908, 0xbb67ae8584caa73b, 0x3c6ef372fe94f82b, 0xa54ff53a5f1d36f1, 0x510e527fade682d1, 0x9b05688c2b3e6c1f, 0x1f83d9abfb41bd6b, 0x5be0cd19137e2179 SHA-512 round constants: k[0..79] := 0x428a2f98d728ae22, 0x7137449123ef65cd, 0xb5c0fbcfec4d3b2f, 0xe9b5dba58189dbbc, 0x3956c25bf348b538, 0x59f111f1b605d019, 0x923f82a4af194f9b, 0xab1c5ed5da6d8118, 0xd807aa98a3030242, 0x12835b0145706fbe, 0x243185be4ee4b28c, 0x550c7dc3d5ffb4e2, 0x72be5d74f27b896f, 0x80deb1fe3b1696b1, 0x9bdc06a725c71235, 0xc19bf174cf692694, 0xe49b69c19ef14ad2, 0xefbe4786384f25e3, 0x0fc19dc68b8cd5b5, 0x240ca1cc77ac9c65, 0x2de92c6f592b0275, 0x4a7484aa6ea6e483, 0x5cb0a9dcbd41fbd4, 0x76f988da831153b5, 0x983e5152ee66dfab, 0xa831c66d2db43210, 0xb00327c898fb213f, 0xbf597fc7beef0ee4, 0xc6e00bf33da88fc2, 0xd5a79147930aa725, 0x06ca6351e003826f, 0x142929670a0e6e70, 0x27b70a8546d22ffc, 0x2e1b21385c26c926, 0x4d2c6dfc5ac42aed, 0x53380d139d95b3df, 0x650a73548baf63de, 0x766a0abb3c77b2a8, 0x81c2c92e47edaee6, 0x92722c851482353b, 0xa2bfe8a14cf10364, 0xa81a664bbc423001, 0xc24b8b70d0f89791, 0xc76c51a30654be30, 0xd192e819d6ef5218, 0xd69906245565a910, 0xf40e35855771202a, 0x106aa07032bbd1b8, 0x19a4c116b8d2d0c8, 0x1e376c085141ab53, 0x2748774cdf8eeb99, 0x34b0bcb5e19b48a8, 0x391c0cb3c5c95a63, 0x4ed8aa4ae3418acb, 0x5b9cca4f7763e373, 0x682e6ff3d6b2b8a3, 0x748f82ee5defb2fc, 0x78a5636f43172f60, 0x84c87814a1f0ab72, 0x8cc702081a6439ec, 0x90befffa23631e28, 0xa4506cebde82bde9, 0xbef9a3f7b2c67915, 0xc67178f2e372532b, 0xca273eceea26619c, 0xd186b8c721c0c207, 0xeada7dd6cde0eb1e, 0xf57d4f7fee6ed178, 0x06f067aa72176fba, 0x0a637dc5a2c898a6, 0x113f9804bef90dae, 0x1b710b35131c471b, 0x28db77f523047d84, 0x32caab7b40c72493, 0x3c9ebe0a15c9bebc, 0x431d67c49c100d4c, 0x4cc5d4becb3e42b6, 0x597f299cfc657e2a, 0x5fcb6fab3ad6faec, 0x6c44198c4a475817 SHA-512 Sum & Sigma: S0 := (a rightrotate 28) xor (a rightrotate 34) xor (a rightrotate 39) S1 := (e rightrotate 14) xor (e rightrotate 18) xor (e rightrotate 41) s0 := (w[i-15] rightrotate 1) xor (w[i-15] rightrotate 8) xor (w[i-15] rightshift 7) s1 := (w[i-2] rightrotate 19) xor (w[i-2] rightrotate 61) xor (w[i-2] rightshift 6)
SHA-384 is identical to SHA-512, except that:
- the initial hash values
h0throughh7are different (taken from the 9th through 16th primes), and - the output is constructed by omitting
h6andh7.
SHA-384 initial hash values (in big-endian):
h[0..7] := 0xcbbb9d5dc1059ed8, 0x629a292a367cd507, 0x9159015a3070dd17, 0x152fecd8f70e5939,
0x67332667ffc00b31, 0x8eb44a8768581511, 0xdb0c2e0d64f98fa7, 0x47b5481dbefa4fa4
SHA-512/t is identical to SHA-512 except that:
- the initial hash values
h0throughh7are given by the SHA-512/t IV generation function, - the output is constructed by truncating the concatenation of
h0throughh7at t bits, - t equal to 384 is not allowed, instead SHA-384 should be used as specified, and
- t values 224 and 256 are especially mentioned as approved.
The SHA-512/t IV generation function evaluates a modified SHA-512 on the ASCII string "SHA-512/t", substituted with the decimal representation of t. The modified SHA-512 is the same as SHA-512 except its initial values h0 through h7 have each been XORed with the hexadecimal constant 0xa5a5a5a5a5a5a5a5.
Sample C implementation for SHA-2 family of hash functions can be found in RFC 6234.
Comparison of SHA functions[edit]
In the table below, internal state means the "internal hash sum" after each compression of a data block.
| Algorithm and variant | Output size (bits) |
Internal state size (bits) |
Block size (bits) |
Rounds | Operations | Security against collision attacks (bits) |
Security against length extension attacks (bits) |
Performance on Skylake (median cpb)[41] | First published | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Long messages | 8 bytes | ||||||||||
| MD5 (as reference) | 128 | 128 (4 × 32) |
512 | 4 (16 operations in each round) |
And, Xor, Or, Rot, Add (mod 232) | ≤ 18 (collisions found)[42] |
0 | 4.99 | 55.00 | 1992 | |
| SHA-0 | 160 | 160 (5 × 32) |
512 | 80 | And, Xor, Or, Rot, Add (mod 232) | < 34 (collisions found) |
0 | ≈ SHA-1 | ≈ SHA-1 | 1993 | |
| SHA-1 | < 63 (collisions found)[43] |
3.47 | 52.00 | 1995 | |||||||
| SHA-2 | SHA-224 SHA-256 |
224 256 |
256 (8 × 32) |
512 | 64 | And, Xor, Or, Rot, Shr, Add (mod 232) |
112 128 |
32 0 |
7.62 7.63 |
84.50 85.25 |
2004 2001 |
| SHA-384 | 384 | 512 (8 × 64) |
1024 | 80 | And, Xor, Or, Rot, Shr, Add (mod 264) |
192 | 128 | 5.12 | 135.75 | 2001 | |
| SHA-512 | 512 | 256 | 0[44] | 5.06 | 135.50 | 2001 | |||||
| SHA-512/224 SHA-512/256 |
224 256 |
112 128 |
288 256 |
≈ SHA-384 | ≈ SHA-384 | 2012 | |||||
| SHA-3 | SHA3-224 SHA3-256 SHA3-384 SHA3-512 |
224 256 384 512 |
1600 (5 × 5 × 64) |
1152 1088 832 576 |
24[45] | And, Xor, Rot, Not | 112 128 192 256 |
448 512 768 1024 |
8.12 8.59 11.06 15.88 |
154.25 155.50 164.00 164.00 |
2015 |
| SHAKE128 SHAKE256 |
d (arbitrary) d (arbitrary) |
1344 1088 |
min(d/2, 128) min(d/2, 256) |
256 512 |
7.08 8.59 |
155.25 155.50 | |||||
In the bitwise operations column, "Rot" stands for rotate no carry, and "Shr" stands for right logical shift. All of these algorithms employ modular addition in some fashion except for SHA-3.
More detailed performance measurements on modern processor architectures are given in the table below.
| CPU architecture | Frequency | Algorithm | Word size (bits) | Cycles/byte x86 | MiB/s x86 | Cycles/byte x86-64 | MiB/s x86-64 |
|---|---|---|---|---|---|---|---|
| Intel Ivy Bridge | 3.5 GHz | SHA-256 | 32 | 16.80 | 199 | 13.05 | 256 |
| SHA-512 | 64 | 43.66 | 76 | 8.48 | 394 | ||
| AMD Piledriver APU | 3.8 GHz | SHA-256 | 32 | 22.87 | 158 | 18.47 | 196 |
| SHA-512 | 64 | 88.36 | 41 | 12.43 | 292 |
The performance numbers labeled 'x86' were running using 32-bit code on 64-bit processors, whereas the 'x86-64' numbers are native 64-bit code. While SHA-256 is designed for 32-bit calculations, it does benefit from code optimized for 64-bit processors on the x86 architecture. 32-bit implementations of SHA-512 are significantly slower than their 64-bit counterparts. Variants of both algorithms with different output sizes will perform similarly, since the message expansion and compression functions are identical, and only the initial hash values and output sizes are different. The best implementations of MD5 and SHA-1 perform between 4.5 and 6 cycles per byte on modern processors.
Testing was performed by the University of Illinois at Chicago on their hydra8 system running an Intel Xeon E3-1275 V2 at a clock speed of 3.5 GHz, and on their hydra9 system running an AMD A10-5800K APU at a clock speed of 3.8 GHz.[46] The referenced cycles per byte speeds above are the median performance of an algorithm digesting a 4,096 byte message using the SUPERCOP cryptographic benchmarking software.[47] The MiB/s performance is extrapolated from the CPU clockspeed on a single core; real-world performance will vary due to a variety of factors.
Implementations[edit]
Below is a list of cryptography libraries that support SHA-2:
- Botan
- Bouncy Castle
- Cryptlib
- Crypto++
- Libgcrypt
- Mbed TLS[48][49]
- libsodium
- Nettle
- LibreSSL
- OpenSSL
- GnuTLS
- wolfSSL
Hardware acceleration is provided by the following processor extensions:
- Intel SHA extensions: Available on some Intel and AMD x86 processors.
- VIA PadLock
- ARMv8 Cryptography Extensions[50]
- IBM z/Architecture: Available since 2005 as part of the Message-Security-Assist Extensions 1 (SHA-256) and 2 (SHA-512)[51]
- IBM Power ISA since v.2.07
See also[edit]
- Comparison of cryptographic hash functions
- Comparison of cryptography libraries
- Hash function security summary
- Hashcash
- HMAC
- International Association for Cryptologic Research (IACR)
- Trusted timestamping
References[edit]
- ^ a b c Dmitry Khovratovich, Christian Rechberger & Alexandra Savelieva (2011). "Bicliques for Preimages: Attacks on Skein-512 and the SHA-2 family" (PDF). IACR Cryptology ePrint Archive. 2011 (286).
- ^ a b c Mario Lamberger & Florian Mendel (2011). "Higher-Order Differential Attack on Reduced SHA-256" (PDF). IACR Cryptology ePrint Archive. 2011 (37).
- ^ Penard, Wouter; van Werkhoven, Tim. "On the Secure Hash Algorithm family" (PDF). staff.science.uu.nl. Archived from the original (PDF) on 2016-03-30.
- ^ a b Federal Register Notice 02-21599, Announcing Approval of FIPS Publication 180-2
- ^ a b "IPR Details: The United States of America as represented by the National Security Agency's general license statement". IETF Datatracker. 858. Retrieved 2008-02-17.
- ^ US 6829355, Lilly, Glenn M., "Device for and method of one-way cryptographic hashing", published 2004-12-07, assigned to National Security Agency
- ^ "FIPS 180-2 with Change Notice 1" (PDF). csrc.nist.gov.
- ^ Federal Register Notice E8-24743, Announcing Approval of FIPS Publication 180-3
- ^ a b Dang, Quynh (2012-08-24). Recommendation for Applications Using Approved Hash Algorithms (Report). National Institute of Standards and Technology.
- ^ a b Barker, Elaine; Barker, William; Burr, William; Polk, W.; Smid, Miles (2012-07-10). Recommendation for Key Management, Part 1: General (Revision 3) (Report). National Institute of Standards and Technology.
- ^ "NIST.gov – Computer Security Division – Computer Security Resource Center". 29 December 2016.
- ^ Barker, Elaine; Roginsky, Allen (2011-01-13). Transitions: Recommendation for Transitioning the Use of Cryptographic Algorithms and Key Lengths (Report). National Institute of Standards and Technology.
- ^ Federal Register Notice 2012-5400, Announcing Approval of FIPS Publication 180-4
- ^ "NIST Selects Winner of Secure Hash Algorithm (SHA-3) Competition". NIST. 2 October 2012. Retrieved 24 February 2015.
- ^ Lucas Daudt Franck; Gabriel Augusto Ginja; João Paulo Carmo; Jose A. Afonso; Maximiliam Luppe (2024). "Custom ASIC Design for SHA-256 Using Open-Source Tools". Computers. 13 (1): 9. doi:10.3390/computers13010009.
- ^ "Verifying authenticity of Debian images". Retrieved 2024-02-19.
- ^ Markoff, John (2009-01-27). "A Tool to Verify Digital Records, Even as Technology Shifts". The New York Times. ISSN 0362-4331. Retrieved 2023-08-27.
- ^ RFC 5702,RFC-Editor.org
- ^ "Unix crypt with SHA-256/512". akkadia.org. Retrieved 2023-08-27.
- ^ Bitcoin, Surplus. "Bitcoin Does Not Waste Energy". Surplus Bitcoin. Archived from the original on 2022-05-28. Retrieved 2020-04-20.
- ^ "What Is SHA-256 And How Is It Related to Bitcoin? - Mycryptopedia". Mycryptopedia. 2017-09-21. Retrieved 2018-09-17.
- ^ Computer Security Division, Information Technology Laboratory (2017-01-04). "NIST Policy on Hash Functions – Hash Functions | CSRC | CSRC". CSRC | NIST. Retrieved 2023-08-27.
- ^ "Secure Hashing". NIST. Archived from the original on 2011-06-25. Retrieved 2010-11-25.
- ^ "Overview of Windows XP Service Pack 3" (PDF). Microsoft Corporation. Archived from the original (PDF) on May 30, 2008.
- ^ "Gradually Sunsetting SHA-1". Chromium Blog. Retrieved 2023-08-27.
- ^ Eric Mill. "SHAAAAAAAAAAAAA". SHAAAAAAAAAAAAA.com.
- ^ "The unofficial Chrome SHA1 deprecation FAQ". Filippo Valsorda. 2015-04-08. Retrieved 2023-08-27.
- ^ "An update to our SHA-1 deprecation roadmap – Microsoft Edge Dev BlogMicrosoft Edge Dev Blog". blogs.windows.com. 29 April 2016. Retrieved 2016-11-28.
- ^ online, heise (2016-01-08). "Firefox: Mozilla schaltet SHA-1 ab … und direkt wieder an". Security (in German). Retrieved 2023-08-27.
- ^ Alexander Sotirov, Marc Stevens, Jacob Appelbaum, Arjen Lenstra, David Molnar, Dag Arne Osvik, Benne de Weger, MD5 considered harmful today: Creating a rogue CA certificate, accessed March 29, 2009.
- ^ Ji Li, Takanori Isobe and Kyoji Shibutani, Sony China Research Laboratory and Sony Corporation, Converting Meet-in-the-Middle Preimage Attack into Pseudo Collision Attack: Application to SHA-2
- ^ Sanadhya, Somitra Kumar; Sarkar, Palash (2008), New collision attacks against up to 24-step SHA-2, Lecture Notes in Computer Science, vol. 5365, Springer-Verlag, pp. 91–103, doi:10.1007/978-3-540-89754-5_8, ISBN 978-3-540-89753-8
- ^ Sanadhya, Somitra Kumar; Sarkar, Palash (2009). "A combinatorial analysis of recent attacks on step reduced SHA-2 family". Cryptography and Communications. doi:10.1007/s12095-009-0011-5.
- ^ Kazumaro Aoki; Jian Guo; Krystian Matusiewicz; Yu Sasaki & Lei Wang (2009). "Preimages for Step-Reduced SHA-2". Advances in Cryptology – ASIACRYPT 2009. Lecture Notes in Computer Science. Vol. 5912. Springer Berlin Heidelberg. pp. 578–597. doi:10.1007/978-3-642-10366-7_34. ISBN 978-3-642-10366-7. ISSN 0302-9743.
- ^ Jian Guo; San Ling; Christian Rechberger & Huaxiong Wang (2010). "Advanced Meet-in-the-Middle Preimage Attacks: First Results on Full Tiger, and Improved Results on MD4 and SHA-2". Advances in Cryptology - ASIACRYPT 2010 (PDF). Lecture Notes in Computer Science. Vol. 6477. Springer Berlin Heidelberg. pp. 56–75. doi:10.1007/978-3-642-17373-8_4. ISBN 978-3-642-17373-8. ISSN 0302-9743.
- ^ Florian Mendel; Tomislav Nad; Martin Schläffer (2013). "Improving Local Collisions: New Attacks on Reduced SHA-256". Advances in Cryptology – EUROCRYPT 2013. Lecture Notes in Computer Science. Vol. 7881. Springer Berlin Heidelberg. pp. 262–278. doi:10.1007/978-3-642-38348-9_16. ISBN 978-3-642-38348-9. ISSN 0302-9743.
- ^ Maria Eichlseder and Florian Mendel and Martin Schläffer (2014). "Branching Heuristics in Differential Collision Search with Applications to SHA-512" (PDF). IACR Cryptology ePrint Archive. 2014 (302).
- ^ Christoph Dobraunig; Maria Eichlseder & Florian Mendel (2016). "Analysis of SHA-512/224 and SHA-512/256" (PDF). International Association for Cryptologic Research.
- ^ Li, Yingxin; Liu, Fukang; Wang, Gaoli (2024). "New Records in Collision Attacks on SHA-2". Cryptology ePrint Archive. Retrieved 2024-03-02.
- ^ "SHS Validation List". NIST. 2017-06-16. Archived from the original on 2017-06-17.
- ^ "Measurements table". bench.cr.yp.to.
- ^ Tao, Xie; Liu, Fanbao; Feng, Dengguo (2013). Fast Collision Attack on MD5 (PDF). Cryptology ePrint Archive (Technical report). IACR.
- ^ Stevens, Marc; Bursztein, Elie; Karpman, Pierre; Albertini, Ange; Markov, Yarik. The first collision for full SHA-1 (PDF) (Technical report). Google Research.
- Marc Stevens; Elie Bursztein; Pierre Karpman; Ange Albertini; Yarik Markov; Alex Petit Bianco; Clement Baisse (February 23, 2017). "Announcing the first SHA1 collision". Google Security Blog.
- ^ Without truncation, the full internal state of the hash function is known, regardless of collision resistance. If the output is truncated, the removed part of the state must be searched for and found before the hash function can be resumed, allowing the attack to proceed.
- ^ "The Keccak sponge function family". Retrieved 2016-01-27.
- ^ SUPERCOP Benchmarks Measurements of hash functions, indexed by machine
- ^ "SUPERCOP". Retrieved 24 February 2015.
- ^ Supported SSL / TLS ciphersuites
- ^ Mbed TLS Changelog, 7 July 2007
- ^ "ARM Cortex-A53 MPCore Processor Technical Reference Manual Cryptography Extension".
- ^ IBM z/Architecture Principles of Operation, publication number SA22-7832. See KIMD and KLMD instructions in Chapter 7.
Further reading[edit]
- Henri Gilbert, Helena Handschuh: Security Analysis of SHA-256 and Sisters. Selected Areas in Cryptography 2003: pp175–193
- "Proposed Revision of Federal Information Processing Standard (FIPS) 180, Secure Hash Standard". Federal Register. 59 (131): 35317–35318. 1994-07-11. Retrieved 2007-04-26.
External links[edit]
- Descriptions of SHA-256, SHA-384, and SHA-512 from NIST
- SHA-2 Checker – SHAChecker to check one's SSL compatibility for SHA-2
- SHA-256 Calculator – SHA-256 Calculator
- SHA-256 Hash Generator – SHA256 Generator – Also serves other critical secure hash algorithms
- Specifications for a Secure Hash Standard (SHS) – Draft for proposed SHS (SHA-0)
- Secure Hash Standard (SHS) – Proposed SHS (SHA-0)
- CSRC Cryptographic Toolkit – Official NIST site for the Secure Hash Standard
- FIPS PUB 180-4: Secure Hash Standard (SHS) (PDF, 834 KB) – Current version of the Secure Hash Standard (SHA-1, SHA-224, SHA-256, SHA-384, and SHA-512), August 2015
- Test vectors for SHA-256/384/512 from the NESSIE project
- Test vectors for SHA-1, SHA-2 from NIST site
- NIST Cryptographic Hash Project – SHA-3 competition
- RFC 3874: "A 224-bit One-way Hash Function: SHA-224"
- RFC 6234: "US Secure Hash Algorithms (SHA and SHA-based HMAC and HKDF)"; contains sample C implementation
- SHA-256 algorithm demonstration





