Benford's law

For the tongue-in-cheek "law" about controversy, see Benford's law of controversy.

A logarithmic scale bar. Picking a random x position on this number line, roughly 30% of the time the first digit of the number will be 1 (the widest band of each power of ten).

Benford's law, also called the first-digit law, states that in lists of numbers from many real-life sources of data, the leading digit is distributed in a specific, non-uniform way. According to this law, the first digit is 1 almost one third of the time, and larger digits occur as the leading digit with lower and lower frequency, to the point where 9 as a first digit occurs less than one time in twenty. The basis for this "law" is that the values of real-world measurements are often distributed logarithmically, thus the logarithm of this set of measurements is generally distributed uniformly.

This counter-intuitive result has been found to apply to a wide variety of data sets, including electricity bills, street addresses, stock prices, population numbers, death rates, lengths of rivers, physical and mathematical constants, and processes described by power laws (which are very common in nature). The result holds regardless of the base in which the numbers are expressed, although the exact proportions change.

It is named after physicist Frank Benford, who stated it in 1938, although it had been previously stated by Simon Newcomb in 1881. Although many "proofs" of this law have been put forth (starting with Newcomb himself), none were mathematically rigorous until Theodore P. Hill's in 1995.

Mathematical statement

Benford's distribution

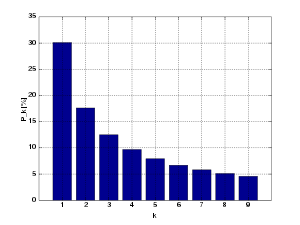
More precisely, Benford's law states that the leading digit d (d ∈ {1, …, b − 1} ) in base b (b ≥ 2) occurs with probability P(d)=log_b(d + 1) − log_bd = log_b((d + 1)/d). This quantity is exactly the space between d and d + 1 in a log scale.

In base 10, the leading digits have the following distribution by Benford's law, where d is the leading digit and p the probability:

d	p
1	30.1%
2	17.6%
3	12.5%
4	9.7%
5	7.9%
6	6.7%
7	5.8%
8	5.1%
9	4.6%

Explanations

Benford's law has been explained from a number of points of view.

Breadth of distributions on logarithmic scale

A broad probability distribution on a log scale

A narrow probability distribution on a log scale

Above are two probability distributions, plotted on a log scale. In each case, the total area in red is the relative probability that the first digit is 1, and the total area in blue is the relative probability that the first digit is 8.

For the left distribution, the ratio of the areas of red and blue appears approximately equal to the ratio of the widths of each red and blue bar. The ratio of the widths is universal and given precisely by Benford's law. Therefore the numbers drawn from this distribution will approximately follow Benford's law.

On the other hand, for the right distribution, the ratio of the areas of red and blue is very different from the ratio of the widths of each red and blue bar. (The widths have the same universal ratio as in the left distribution.) Rather, the relative areas of red and blue are determined more by the height of the bars than the widths. The heights, unlike the widths, do not satisfy the universal relationship of Benford's law; instead, they are determined entirely by the shape of the distribution in question. Accordingly, the first digits in this distribution do not satisfy Benford's law at all.

More generally, distributions that cover many orders of magnitude rather smoothly (e.g. income distributions, or populations of towns and cities) are likely to satisfy Benford's law to a very good approximation, like the left distribution. On the other hand, a distribution that covers only one or two orders of magnitude, or less (e.g. heights of human adults, or IQ scores) is unlikely to satisfy Benford's law well, like the right distribution.

Outcomes of exponential growth processes

The precise form of Benford's law can be explained if one assumes that the logarithms of the numbers are uniformly distributed; this means that a number is for instance just as likely to be between 100 and 1000 (logarithm between 2 and 3) as it is between 10,000 and 100,000 (logarithm between 4 and 5). For many sets of numbers, especially ones that grow exponentially such as incomes and stock prices, this is a reasonable assumption.

A simple example may help clarify how this works. To say that a quantity is "growing exponentially" is just another way of saying that its doubling time is constant. If the quantity takes a year to double, then after one more year, it has doubled again. Thus it will be four times its original value at the end of the second year, eight times its original value at the end of the third year, and so on. Suppose we start the timer when a quantity that is doubling every year has reached the value of 100. Its value will have a leading digit of 1 for the entire first year. During the second year, its value will have a leading digit of 2 for a little over seven months, and 3 for the remaining five. During the third year, the leading digit will pass through 4, 5, 6, and 7, spending less and less time with each succeeding digit. Fairly early in the fourth year, the leading digits will pass through 8 and 9. Then the quantity's value will have reached 1000, and the process starts again. From this example, it's easy to see that if you sampled the quantity's value at random times throughout those years, you're more likely to have measured it when the value of its leading digit was 1, and successively less likely to have measured it when the value was moving through increasingly higher leading digits.

This example makes it plausible that data tables that involve measurements of exponentially growing quantities will agree with Benford's Law. But the Law also appears to hold for many cases where an exponential growth pattern is not obvious.

Frequency of first significant digit of physical constants plotted against Benford's Law.

Scale invariance

The law can alternatively be explained by the fact that, if it is indeed true that the first digits have a particular distribution, it must be independent of the measuring units used. For example, this means that if one converts from e.g. feet to yards (multiplication by a constant), the distribution must be unchanged — it is scale invariant, and the only distribution that fits this is one whose logarithm is uniformly distributed.

For example, the first (non-zero) digit of the lengths or distances of objects should have the same distribution whether the unit of measurement is feet, yards, or anything else. But there are three feet in a yard, so the probability that the first digit of a length in yards is 1 must be the same as the probability that the first digit of a length in feet starts 3, 4, or 5. Applying this to all possible measurement scales gives a logarithmic distribution, and combined with the fact that log₁₀(1) = 0 and log₁₀(10) = 1 gives Benford's law. That is, if there is a distribution of first digits, it must apply to a set of data regardless of what measuring units are used, and the only distribution of first digits that fits that is the Benford Law.

For each positive integer n, this graph shows the probability that a random integer between 1 and n starts with each of the nine possible digits. For any particular value of n, the probabilities do not precisely satisfy Benford's law; however, looking at a variety of different values of n and averaging the probabilities for each, the resulting probabilities do exactly satisfy Benford's law.

Multiple probability distributions

Note that for numbers drawn from many distributions, for example IQ scores, human heights or other variables following normal distributions, the law is not valid. However, if one "mixes" numbers from those distributions, for example by taking numbers from newspaper articles, Benford's law reappears. This can be proven mathematically: if one repeatedly "randomly" chooses a probability distribution and then randomly chooses a number according to that distribution, the resulting list of numbers will obey Benford's law.

Applications and limitations

In 1972, Hal Varian suggested that the law could be used to detect possible fraud in lists of socio-economic data submitted in support of public planning decisions. Based on the plausible assumption that people who make up figures tend to distribute their digits fairly uniformly, a simple comparison of first-digit frequency distribution from the data with the expected distribution according to Benford's law ought to show up any anomalous results. Following this idea, Nigrini showed that Benford's law could be used as an indicator of accounting and expenses fraud.

Limitations

Care must be taken with these applications, however. A set of real-life data may not obey the law, depending on the extent to which the distribution of numbers it contains are skewed by the category of data.

For instance, one might expect a list of numbers representing 'populations of UK villages beginning with 'A' or 'small insurance claims' to obey Benford's law. But if it turns out that the definition of a 'village' is 'settlement with population between 300 and 999', or that the definition of a 'small insurance claim' is 'claim between $50 and $100', then Benford's law would not apply because certain numbers have been excluded by the definition.

History

The discovery of this fact goes back to 1881, when the American astronomer Simon Newcomb noticed that in logarithm books (used at that time to perform calculations), the earlier pages (which contained numbers that started with 1) were much more worn than the other pages. It has been argued that any book that is used from the beginning would show more wear and tear on the earlier pages, but also that Newcomb would have been referring to dirt on the pages themselves (rather than the edges) where people ran their fingers down the lists of digits to find the closest number to the one they required.

However, logarithm books did contain more than one list, with both logarithms and antilogarithms present, and sometimes many other tables as well, including exponentials, roots, sines, cosines, tangents, secants, cosecants etc., thus, this story may be apocryphal. However, Newcomb's published result is the first known instance of this observation and includes a distribution on the second digit, as well. Newcomb proposed a law that the probability of a single number being the first digit of a number (let such a first digit be N) was equal to log(N+1)-log(N).

The phenomenon was rediscovered in 1938 by the physicist Frank Benford, who checked it on a wide variety of data sets and was credited for it. In 1996, Ted Hill proved the result about mixed distributions mentioned above.

Generalization to digits beyond the first

It is possible to extend the law to digits beyond the first. In particular, the probability of encountering a number starting with the string of digits n is given by:

$\log _{10}\left(n+1\right)-\log _{10}\left(n\right)=\log _{10}\left(1+{\frac {1}{n}}\right).$

(For example, the probability that a number starts with the digits 3,1,4 is log₁₀(1 + 1/314).) This result can be used to find the probability that a particular digit occurs at a given position within a number. For instance, the probability that a "2" is encountered as the second digit is

$\log _{10}\left(1+{\frac {1}{12}}\right)+\log _{10}\left(1+{\frac {1}{22}}\right)+\cdots +\log _{10}\left(1+{\frac {1}{92}}\right)\approx 0.109.$

The distribution of the nth digit, as n increases, rapidly approaches a uniform distribution with 10% for each of the ten digits.

In practice, applications of Benford's law routinely use more than the first digit.

See also

• Forensic accounting
• Auditing

Other references

• Sehity; et al. (2005). "Price developments after a nominal shock: Benford's Law and psychological pricing after the euro introduction". International Journal of Research in Marketing. 22: 471–480. doi:10.1016/j.ijresmar.2005.09.002. {{cite journal}}: Explicit use of et al. in: |author= (help)
• Wendy Cho and Brian Gaines (2007). "Breaking the (Benford) Law: statistical fraud detection in campaign finance". The American Statistician. 61 (3): 218–223. doi:10.1198/000313007X223496. {{cite journal}}: Unknown parameter |month= ignored (help)
• L.V.Furlan (1948). "Die Harmoniegesetz der Statistik: Eune Untersuchung uber die metrische Interdependenz der soziale Erscheinungen". Reviewed in Journal of the American Statistical Association. 43 (242): 325–328. {{cite journal}}: Unknown parameter |month= ignored (help)

External links

• Benford's Law and Zipf's Law at cut-the-knot
• Following Benford's Law, or Looking Out for No. 1
• I've Got Your Number by Mark Nigrini
• Video showing Benford's Law applied to Web Data (incl. Minnesota Lakes, US Census Data and Digg Statistics)
• A further five numbers: number 1 and Benford's law by Simon Singh
• Looking out for number one by Jon Walthoe, Robert Hunt and Mike Pearson, plus Magazine, September 1999
• Weisstein, Eric W. "Benford's Law". MathWorld.
• Benford's Law at MathPages
• Mystery of Benford's Law solved by DSP
• Benford's Law from Ratios of Random Numbers by Fiona Maclachlan, Wolfram Demonstrations Project.
• Ted Hill's personal website, in particular his CV, lists his many publications about Benford's law, along with free links to most of them.
• Entropy Principle in Direct Derivation of Benford's Law on the arXiv. Authors: Oded Kafri