Double group

The character tables of the binary tetrahedral, octahedral and icosahedral groups following Frobenius (1899)

In applied mathematics, double groups are groups composed of rotations and related transformations. More specifically, a double group is a central extension of a finite subgroup of the group of three-dimensional rotations by the two-element cyclic group. These include the binary polyhedral groups. They are employed in the field of physical chemistry.

G. Frobenius derived and listed in 1899 the character tables of the finite subgroups of SU(2), the double cover of the rotation group SO(3). In 1875, F. Klein had already classified these finite "binary" subgroups into the cyclic groups, the binary dihedral groups, the binary tetrahedral group, the binary octahedral group and the binary icosahedral group. Alternative derivations of the character tables were given by I. Schur and H. E. Jordan in 1907; further branching rules and tensor product formulas were also determined.

In a landmark 1929 article on splitting of atoms in crystals, the physicist H. Bethe coined the term "double group" (Doppelgruppe), a concept that allowed double-valued or spinor representations of finite subgroups of the rotation group to be regarded as ordinary linear representations of their double covers. In particular, Bethe applied his theory to relativistic quantum mechanics and crystallographic point groups, where a natural physical restriction to 32 point groups occurs. Subsequently, the non-crystallographic icosahedral case has also been investigated more extensively, resulting most recently in groundbreaking advances on carbon 60 and fullerenes in the 1980s and 90s, for which R. Curl, H. Kroto and R. Smalley were jointly awarded a Nobel Prize in Chemistry in 1996. In 1982–1984, there was another breakthrough involving the icocahedral group, this time through materials scientist Dan Shechtman's remarkable work on quasicrystals, for which he was awarded a Nobel Prize in Chemistry in 2011.

In physical chemistry, double groups are used in the treatment of the magnetochemistry of complexes of metal ions that have a single unpaired electron in the d-shell or f-shell. Instances when a double group is commonly used include 6-coordinate complexes of copper(II), titanium(III) and cerium(III).

In these double groups rotation by 360° is treated as a symmetry operation, R, separate from the identity operation, E; the double group is formed by combining the symmetry operations the group {E,R} with the symmetry operations of a point group such as D₄ or O_h.

Definition and theory

Let Γ be a finite subgroup of SO(3), the three-dimensional rotation group. There is a natural homomorphism f of SU(2) onto SO(3) which has kernel {±I}. This double cover can be realised using the adjoint action of SU(2) on the Lie algebra of traceless 2-by-2 skew-adjoint matrices or using the action by conjugation of unit quaternions. The double group Γ' is defined as f^–1 (Γ). By construction {±I} is a central subgroup of Γ' and the quotient is isomorphic to Γ. Thus Γ' is a central extension of the group Γ by {±1}, the cyclic group of order 2. Ordinary representations of Γ' are just mappings of Γ into the general linear group that are homomorphisms up to a sign; equivalently, they are projective representations of Γ with a factor system or Schur multiplier in {±1}. Two projective representations of Γ are closed under the tensor product operation, with their corresponding factor systems in {±1} multiplying. The central extensions of Γ by {±1} also have a natural product.

The finite subgroups of SU(2) and SO(3) were determined in 1876 by Felix Klein in an article in Mathematische Annalen, later incorporated in his celebrated 1884 "Lectures on the Icosahedron": for SU(2), the subgroups correspond to the cyclic groups, the binary dihedral groups, the binary tetrahedral group, the binary octahedral group, and the binary icosahedral group; and for SO(3), they correspond to the cyclic groups, the dihedral groups, the tetrahedral group, the octahedral group and the icosahedral group. The correspondence can be found in numerous text books, and goes back to the classification of platonic solids. From Klein's classifications of binary subgroups, it follows that, if Γ a finite subgroup of SO(3), then, up to equivalence, there are exactly two central extensions of Γ by {±1}: the one obtained by lifting the double cover Γ' = f^–1 (Γ); and the trivial extension Γ x {±1}.

The character tables of the finite subgroups of SU(2) and SO(3) were determined and tabulated by F. G. Frobenius in 1898, with alternative derivations by I. Schur and H. E. Jordan in 1907 independently. Branching rules and tensor product formulas were also determined. For each binary subgroup, i.e. finite subgroup of SU(2), the irreducible representations of Γ are labelled by extended Dynkin diagrams of type A, D and E; the rules for tensoring with the two-dimensional vector representation are given graphically by an undirected graph. By Schur's lemma, irreducible representations of Γ x {±1} are just irreducible representations of Γ multiplied by either the trivial or the sign character of {±1}. Likewise, irreducible representations of Γ' which send –1 to I are just ordinary representations of Γ; while those which send –1 to –I are genuinely double-valued or spinor representations.

Example. For the double icosahedral group, if $\varphi$ is the golden ratio ${1 \over 2}(1+{\sqrt {5}})$ with inverse ${\tilde {\varphi }}={1 \over 2}(-1+{\sqrt {5}})$, the character table is given below: spinor characters are denoted by asterisks. The character table of the icosahedral group is also given.

Character table: double icosahedral group

$I_{h}^{\prime }$	1	12C2[5]	12C3[5]	1C4[2]	12C5[10]	12C6[10]	20C7[3]	20C8[6]	30C9[4]
$\chi _{1}$	1	1	1	1	1	1	1	1	1
$\chi _{3}$	3	$\varphi$	$-{\tilde {\varphi }}$	3	$-{\tilde {\varphi }}$	$\varphi$	0	0	–1
$\chi _{3^{\prime }}$	3	$-{\tilde {\varphi }}$	$\varphi$	3	$\varphi$	$-{\tilde {\varphi }}$	0	0	–1
$\chi _{4}$	4	–1	–1	4	–1	–1	1	1	0
$\chi _{5}$	5	0	0	5	0	0	–1	–1	0
$\chi _{2}^{*}$	2	$-\varphi$	${\tilde {\varphi }}$	–2	$-{\tilde {\varphi }}$	$\varphi$	–1	1	0
$\chi _{2^{\prime }}^{*}$	2	${\tilde {\varphi }}$	$-\varphi$	–2	$\varphi$	$-{\tilde {\varphi }}$	–1	1	0
$\chi _{4}^{*}$	4	–1	–1	-4	–1	–1	1	0	–1
$\chi _{6}^{*}$	6	1	1	–6	–1	–1	0	0	0

Character table: icosahedral group

$I_{h}$	1	20C2[3]	15C3[2]	12C4[5]	12C5[5]
$\chi _{1}$	1	1	1	1	1
$\chi _{3}$	3	0	–1	$\varphi$	$-{\tilde {\varphi }}$
$\chi _{3^{\prime }}$	3	0	–1	$-{\tilde {\varphi }}$	$\varphi$
$\chi _{4}$	4	1	0	–1	–1
$\chi _{5}$	5	–1	1	0	0

The tensor product rules for tensoring with the two-dimensional representation are encoded diagrammatically below:

The numbering has at the top $\chi _{3^{\prime }}$ and then below, from left to right, $\chi _{2^{\prime }}^{*}$, $\chi _{4}$, $\chi _{6}^{*}$, $\chi _{5}$, $\chi _{4}^{*}$, $\chi _{3}$, $\chi _{2}^{*}$, and $\chi _{1}$. Thus, on labelling the vertices by irreducible characters, the result of multiplying $\chi _{2}^{*}$ by a given irreducible character equals the sum of all irreducible characters labelled by an adjacent vertex.

The representation theory of SU(2) goes back to the nineteenth century and the theory of invariants of binary forms, with the figures of Alfred Clebsch and Paul Gordan prominent. The irreducible representations of SU(2) are indexed by non-negative half integers j. If V is the two-dimensional vector representation, then V_j = S^2j V, the 2jth symmetric power of V, a (2j + 1)-dimensional vector space. Letting G be the compact group SU(2), the group G acts irreducibly on each V_j and satisfies the Clebsch-Gordan rules:

$V_{i}\otimes V_{j}\cong V_{|i-j|}\oplus V_{|i-j|+1}\oplus \cdots \oplus V_{i+j-1}\oplus V_{i+j}.$

In particular $V_{j}\otimes V_{1 \over 2}\cong V_{j-{1 \over 2}}\oplus V_{j+{1 \over 2}}$ for j > 0, and $V_{0}\otimes V_{1 \over 2}\cong V_{1 \over 2}.$ By definition, the matrix representing g in V_j is just S^2j ( g ). Since every g is conjugate to a diagonal matrix with diagonal entries $\zeta$ and $\zeta ^{-1}$ (the order being immaterial), in this case S^2j ( g ) has diagonal entries $\zeta ^{2j}$, $\zeta ^{2j-1}$, ... ,$\zeta ^{-2j+1}$, $\zeta ^{-2j}$. Setting $\pi _{j}(g)=S^{2j}(g),$ this yields the character formula

$\chi _{j}(g):={\rm {Tr}}\,\pi _{j}(g)=\sum _{k=-2j}^{2j}\zeta ^{k}={\zeta ^{2j+1}-\zeta ^{-2j-1} \over \zeta -\zeta ^{-1}}.$

Substituting $\zeta =e^{i\theta }$, it follows that, if g has diagonal entries $e^{\pm i\theta },$ then

$\chi _{j}(g)={\sin(2j+1)\theta \over \sin \theta }.$

The representation theory of SU(2), including that of SO(3), can be developed in many different ways:

• using the complexification G_c = SL(2,C) and the double coset decomposition G_c = B · w · B ∐ B, where B denotes upper triangular matrices and $w={\begin{pmatrix}0&1\\-1&0\end{pmatrix}}$;
• using the infinitesimal action of the Lie algebras of SU(2) and SL(2,C) where they appear as raising and lowering operators E, F, H of angular momentum in quantum mechanics: here E = ${\begin{pmatrix}0&1\\0&0\end{pmatrix}}$, F = E* and H = [E,F] so that [H,E] = 2E and [H,F] = –2F;
• using integration of class functions over SU(2), identifying the unit quaternions with 3-sphere and Haar measure as the volume form: this reduces to integration over the diagonal matrices, i.e. the circle group T.

The properties of matrix coefficients or representative functions of the compact group SU(2) (and SO(3)) are well documented as part of the theory of special functions: the Casimir operator C = H² + 2 EF + 2 FE commutes with the Lie algebras and groups. The operator ¼ C can be identified with the Laplacian Δ, so that on a matrix coefficient φ of V_j, Δφ =(j² + j)φ.

The representative functions A have two multiplicative structures: pointwise multiplication and convolution with respect to Haar measure μ. In turn μ defines a non-degenerate symmetric form μ(a ⋅ b); and ε, evaluation at 1, likewise ε(a $\star$ b). The antipode S is an antiautomorphism for both structures, given by Sa(g) = a(g⁻¹⁾, with the compatibility condition $\phi (a\cdot b)=\varepsilon (S(a)\star b)$. This is equivalent to the usual Hopf algebra structure. For a finite group Γ, such as a finite subgroup of SU(2), the finite-dimensional group algebra C[Γ] and function algebra C^Γ have entirely analogous roles.

From the Clebsch-Gordan rules, the convolution algebra A is isomorphic to a direct sum of n x n matrices, with n = 2j + 1 and j ≥ 0. The matrix coefficients for each irreducible representation V_j form a set of matrix units. This direct sum decomposition is the Peter-Weyl theorem. The corresponding result for C[Γ] is Maschke's theorem.

Background

In magnetochemistry, the need for a double group arises in a very particular circumstance, namely, in the treatment of the magnetic properties of complexes of a metal ion in whose electronic structure there is a single unpaired electron (or its equivalent, a single vacancy) in a metal ion's d- or f- shell. This occurs, for example, with the elements copper, silver and gold in the +2 oxidation state, where there is a single vacancy in the d-electron shell, with titanium(III) which has a single electron in the 3d shell and with cerium(III) which has a single electron in the 4f shell.

In group theory, the character $\chi$, for rotation, by an angle α, of a wavefunction for half-integer angular momentum is given by

$\chi ^{J}(\alpha )={\frac {\sin[J+1/2]\alpha }{\sin(1/2)\alpha }}$

where angular momentum is the vector sum of spin and orbital momentum, $J=L+S$. This formula applies with angular momentum in general.

In atoms with a single unpaired electron the character for a rotation through an angle of $2\pi +\alpha$ is equal to $-\chi ^{J}(\alpha )$. The change of sign cannot be true for an identity operation in any point group. Therefore, a double group, in which rotation by $2\pi$ is classified as being distinct from the identity operation, is used. A character table for the double group D'₄ is as follows. The new operation is labelled R in this example. The character table for the point group D₄ is shown for comparison.

Character table: double group D'₄

D'4			C4	C43	C2	2C'2	2C''2
	E	R	C4R	C43R	C2R	2C'2R	2C''2R
A'1	1	1	1	1	1	1	1
A'2	1	1	1	1	1	-1	-1
B'1	1	1	-1	-1	1	1	-1
B'2	1	1	-1	-1	1	-1	1
E'1	2	-2	0	0	-2	0	0
E'2	2	-2	√2	-√2	0	0	0
E'3	2	-2	-√2	√2	0	0	0

Character table: point group D₄

D4	E	2 C4	C2	2 C2'	2 C2
A1	1	1	1	1	1 +
A2	1	1	1	−1	−1
B1	1	−1	1	1	−1
B2	1	−1	1	−1	1
E	2	0	−2	0	0

In the table for the double group, the symmetry operations such as C₄ and C₄R belong to the same class but the header is shown, for convenience, in two rows, rather than C₄, C₄R in a single row .

Character tables for the double groups T', O', T_d', D_3h', C_6v', D₆', D_2d', C_4v', D₄', C_3v', D₃', C_2v', D₂' and R(3)' are given in Koster et al. (1963), Salthouse & Ware (1972) and Cornwell (1984).

Applications

Sub-structure at the center of an octahedral complex

Structure of a square-planar complex ion such as [AgF₄]^2-

An atom or ion (red) held in a C₆₀ fullerene cage

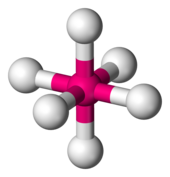
The need for a double group occurs, for example, in the treatment of magnetic properties of 6-coordinate complexes of copper(II). The electronic configuration of the central Cu²⁺ ion can be written as [Ar]3d⁹. It can be said that there is a single vacancy, or hole, in the copper 3d-electron shell, which can contain up to 10 electrons. The ion [Cu(H₂O)₆]²⁺ is a typical example of a compound with this characteristic.

(1) Six-coordinate complexes of the Cu(II) ion, with the generic formula [CuL₆]²⁺, are subject to the Jahn-Teller effect so that the symmetry is reduced from octahedral (point group O_h) to tetragonal (point group D_4h). Since d orbitals are centrosymmetric the related atomic term symbols can be classified in the subgroup D₄ .

(2) To a first approximation spin-orbit coupling can be ignored and the magnetic moment is then predicted to be 1.73 Bohr magnetons, the so-called spin-only value. However, for a more accurate prediction spin-orbit coupling must be taken into consideration. This means that the relevant quantum number is J, where J = L + S.

(3) When J is half-integer, the character for a rotation by an angle of α + 2π radians is equal to minus the character for rotation by an angle α. This cannot be true for an identity in a point group. Consequently, a group must be used in which rotations by α + 2π are classed as symmetry operations distinct from rotations by an angle α. This group is known as the double group, D₄'.

With species such as the square-planar complex of the silver(II) ion [AgF₄]^2- the relevant double group is also D₄'; deviations from the spin-only value are greater as the magnitude of spin-orbit coupling is greater for silver(II) than for copper(II).

A double group is also used for some compounds of titanium in the +3 oxidation state. Compounds of titanium(III) have a single electron in the 3d shell. The magnetic moments of octahedral complexes with the generic formula [TiL₆]ⁿ⁺ have been found to lie in the range 1.63 - 1.81 B.M. at room temperature. The double group O' is used to classify their electronic states.

The cerium(III) ion, Ce³⁺, has a single electron in the 4f shell. The magnetic properties of octahedral complexes of this ion are treated using the double group O'.

When a cerium(III) ion is encapsulated in a C₆₀ cage, the formula of the endohedral fullerene is written as {Ce³⁺@C₆₀^3-}.

Free radicals

Double groups may be used in connection with free radicals. This has been illustrated for the species CH₃F⁺ and CH₃BF₂⁺ which both contain a single unpaired electron.

See also

• McKay graph
• ADE classification
• Molecular symmetry
• Point group
• Space group

Further reading

• Lipson, R.H. "Spin-orbit coupling and double groups". (web site)
• Earnshaw, Alan (1968). Introduction to Magnetochemistry. Academic Press.
• Figgis, B.N.; Lewis, J. (1960). "The Magnetochemistry of Complex Compounds". In Lewis. J. and Wilkins. R.G. (ed.). Modern Coordination Chemistry. New York: Wiley.
• Orchard, A.F. (2003). Magnetochemistry. Oxford Chemistry Primers. Oxford University Press. ISBN 0-19-879278-6.
• Vulfson, Sergey G.; Arshinova, Rose P. (1998). Molecular Magnetochemistry. Taylor & Francis. ISBN 90-5699-535-9.