Truncation (geometry)

In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex.
Uniform truncation
In general any polyhedron (or polytope) can also be truncated with a degree of freedom how deep the cut is, as shown in Conway polyhedron notation truncation operation.
A special kind of truncation, usually implied, is a uniform truncation, a truncation operator applied to a regular polyhedron (or regular polytope) which creates a resulting uniform polyhedron (uniform polytope) with equal edge lengths. There are no degrees of freedom, and it represents a fixed geometric, just like the regular polyhedra.
More abstractly any uniform polytope defined by a Coxeter-Dynkin diagram with a single ring, can be also uniformly truncated, although it is not a geometric operation, but requires adjusted proportions to reach uniformity. For example Kepler's truncated icosidodecahedron represents a uniform truncation of the icosidodecahedron. It isn't a geometric truncation, which would produce rectangular faces, but a topological truncation that has been adjusted to fit the uniformity requirement.
Truncation of polygons
A truncated n-sided polygon will have 2n sides (edges). A regular polygon uniformly truncated will become another regular polygon: t{n} is {2n}.
Star polygons can also be truncated. A truncated pentagram {5/2} will look like a pentagon, but is actually a double-covered (degenerate) decagon with two sets of overlapping vertices and edges.
Truncation in regular polyhedra and tilings
When the term applies to truncating platonic solids or regular tilings, usually "uniform truncation" is implied, which means to truncate until the original faces become regular polygons with double the sides.
This sequence shows an example of the truncation of a cube, using four steps of a continuous truncating process between a full cube and a rectified cube. The final polyhedron is a cuboctahedron.
The middle image is the uniform truncated cube. It is represented by an extended Schläfli symbol t0,1{p,q,...}.
Other truncations
In quasiregular polyhedra, a truncation is a more qualitative term where some other adjustments are made to adjust truncated faces to become regular. These are sometimes called rhombitruncations.
For example, the truncated cuboctahedron is not really a truncation since the cut vertices of the cuboctahedron would form rectangular faces rather than squares, so a wider operation is needed to adjust the polyhedron to fit desired squares.
In the quasiregular duals, an alternate truncation operation only truncates alternate vertices. (This operation can also apply to any zonohedron which have even-sided faces.)
The dual operation to truncation is the construction of a Kleetope.
Uniform polyhedron and tiling examples
This table shows the truncation progression between the regular forms, with the rectified forms (full truncation) in the center. Comparable faces are colored red and yellow to show the continuum in the sequences.
Prismatic polyhedron examples
| Family | Original | Truncation | Rectification (And dual) |
|---|---|---|---|
| [2,p] |  Hexagonal hosohedron (As spherical tiling) {2,p} |
Hexagonal prism t{2,p} |
 Hexagonal dihedron (As spherical tiling) {p,2} |
rhombitruncated examples
These forms start with a rectified regular form which is truncated. The vertices are order-4, and a true geometric truncation would create rectangular faces. The uniform rhombitruction requires adjustment to create square faces.
| Original | Rectification | Rhombitruncation |
|---|---|---|
 |
 |
 Truncated octahedron |

|
 Cuboctahedron |
 Truncated cuboctahedron |

|
 Icosidodecahedron |
 Truncated icosidodecahedron |

|
 Trihexagonal tiling |
 Truncated trihexagonal tiling or great rhombitrihexagonal tiling |

|
 Triheptagonal tiling |
 Truncated triheptagonal tiling or great rhombitriheptagonal tiling |

|
 Trioctagonal tiling |
 Truncated trioctagonal tiling or great rhombitrioctagonal tiling |

|
 Square tiling |
 Truncated square tiling |

|
 Tetrapentagonal tiling |
 Truncated tetrapentagonal tiling |

|
 Order-4 pentagonal tiling |
 Order-4 truncated pentagonal tiling |
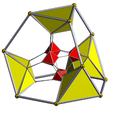
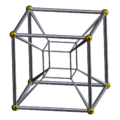
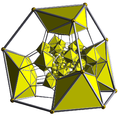
Truncation in polychora and honeycomb tessellation
A regular polychoron or tessellation {p,q,r}, truncated becomes a uniform polychoron or tessellation with 2 cells: truncated {p,q}, and {q,r} cells are created on the truncated section.
See: uniform polychoron and convex uniform honeycomb.
See also
- uniform polyhedron
- uniform polychoron
- Bitruncation (geometry)
- Rectification (geometry)
- Alternation (geometry)
- Conway polyhedron notation
References
- Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8 (pp.145-154 Chapter 8: Truncation)
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
External links
- Weisstein, Eric W. "Truncation". MathWorld.
- Olshevsky, George. "Truncation". Glossary for Hyperspace. Archived from the original on 4 February 2007.
- Polyhedra Names, truncation