Talk:Cantor set

Intro defines Cantor set incorrectly (intro is wrong)

A Cantor set is a compact perfect set with empty interior. A dynamically defined Cantor set is a Cantor set that may be defined by a family of contacting map (see for example the book by Palis-Takens [1], page 53). One may call "The Cantor set" the set defined by "removing the middle third".

Cantor himself defined his set as a perfect set that is nowhere dense. He constructs the thing in several ways. I don't think he even mentions the bit about "removing the middle third" except maybe half way through the paper, as an example, and then, only in passing. At least that's how I remember it going.

I don't mind that the majority of the article is devoted to a simple example that is pounded to death; but the intro should at least give the correct definition, and note that the "middle third" construction is just an example. linas 05:03, 26 July 2005 (UTC)

Could you give a link to a reference, cause I can't find anything about his original definition online. Well.. if you ever revisit this site.. Fresheneesz 22:04, 3 March 2006 (UTC)

?? The reference to Cantor's paper is given in "historical references" at the bottom of the article. You can get the book on amazon for about $8 or so, and most university libraries will have it. It is a rather mind-opening read, espcially if all that you know about the Cantor set comes from the crappy descriptions given in pop-lit books on fractals (which is all I knew when I embarked on this journey). I'm guessing most books on topology will also discuss it; I don't think they do the "middle third" contruction either. linas 22:53, 3 March 2006 (UTC)

Hmm, maybe I'll look it up at the library here. But I kinda doubt I have enough background on the subject. Why don't you correct this page? Fresheneesz 20:23, 5 March 2006 (UTC)

I don't think they do the "middle third" contruction either. Actually, all the books of topology I know do just that. In fact, all sources I know use the term "Cantor set" to denote the "middle third" construction. —Tobias Bergemann 08:31, 6 March 2006 (UTC)

Julian F. Fleron from a Note in Mathematics Magazine, Vol. 67, No 2 (Apr 1994) [stable URL: http://wwww.jstor.org/stable/2690689 ] writes that his first reference to the Cantor ternary set is in a footnote to the statement that “perfect sets need not be everywhere dense” on page 575 of his original paper [referenced below]. She quotes him describing it as: The set of real numbers of the form $$ x= \frac{c-1}{3} + \dots + \frac{c_v}{3^v} + \dots $$ where $c_v$ is $0$ or $2$ for each integer $v$. Zimri2 (talk) 02:40, 17 September 2017 (UTC)

The introductory paragraph and the closing "historical remarks" have virtually identical sentences. Someone with time on their hands might want to tidy up the redundancy. 116.197.236.12 03:22, 17 September 2007 (UTC)

Missing the Significance?

It doesn't seem the article hits on the significance of his discovery in being that the axiom "The sum is larger than any part" is incorrect, but as he demonstrates they can be shown to be equal. The underlying work, Cantor working in base three, used only those base three numbers for his set that did not feature the numeral one. So, base three decimal expansions of for example 0.02202 and 0.202 would be included, while 0.22221 and 0.11201 would be excluded from his set. Taking all these base three numbers, Cantor ingeniuosly directly compared the numbers in his set 'one ot one' to EVERY number on the number line in base 2. So, from above 0.02202 in base 3 becomes in base 2 0.01101, and 0.202 becomes 0.101. So there is a 'one to one' partner for every single decimal expansion in base two from his base three set, even though he removed nearly all the numbers. So he demonstrated a part can be equal to the whole, and demonstrated some unrecognized at that time property of infinity. — Preceding unsigned comment added by 63.139.216.34 (talk) 15:56, 18 October 2011 (UTC)

The thing about it is

The thing about the Cantor set in mathematics is that the term is used much more often to denote any topological space homeomorphic to the basic middle-thirds example than that example itself. So even though this article mistakenly pretends that the term properly refers to the middle thirds example and that everything else is some kind of special use of the term, things are just the other way around to mathematicians.

Yes, most topology textbooks describe the middle thirds construction as the introduction to the Cantor set. But then they define "a Cantor set" as any topological space that's topologically equivalent to it. Then comes the beautiful characterization of it as any topological space that is compact, totally disconnected, dense-in-itself, and metrizable.

It's also kind of amazing that a set that's totally disconnected is also dense-in-itself (every point is a limit point), since the two properties seem almost contradictory.Daqu (talk) 23:38, 27 September 2014 (UTC)

Note: Wikipedia has two articles, namely Cantor set and Cantor space. Should they be merged to reduce the confusion? – Tobias Bergemann (talk) 08:15, 24 July 2015 (UTC)set"

homeomorphic

Before, I claimed that the Cantor set is homeomorphic to the p-adic integers; now I'm not so sure and I played it safe and replaced "p-adic" by "2-adic". Does anybody know if the 3-adic's are homeomorphic to our Cantor set? --AxelBoldt

Yes. Every nonempty totally-disconnected perfect compact metric space is homeomorphic to the Cantor set. --Zundark, 2001 Nov 30

Nice linking

I just thought it was cool to note that in this statement:

The Cantor set can be characterized by these properties: every nonempty totally-disconnected perfect compact metric space is homeomorphic to the Cantor set.

Despite the massive number of adjectives, (nearly) every one of them had already been linked somewhere above. This is good cross-referencing.

Deco 01:07, 27 Nov 2003 (UTC)

Removed textual picture

  0                         1/3                       2/3                         1
  =================================================================================
  ===========================                           ===========================
  =========         =========                           =========         =========
  ===   ===         ===   ===                           ===   ===         ===   ===
  = =   = =         = =   = =                           = =   = =         = =   = =

Gadykozma 07:02, 15 Jul 2004 (UTC)

Image Problem

The image in the page (Cantor_set_in_seven_iterations.png) prints solid black from my (Linux) system, although it displays properly. Has anyone else encountered this? Would there be an objection to the image being modified so that the transparent bits are white? Sasha 17:56, 18 April 2006 (UTC)

The trigonometric-series origins of Cantor's set theory

Mr. 4 numbers, I didn't understand your addition. Did he have in mind a CONCRETE example of a series diverging on the cantor set (as is implied by the word "particular")? I find it hard to believe, such series were found much later. Maybe you are confusing this with the problem of uniqueness (see set of uniqueness)? What's your reference for this information? Gadykozma 10:55, 29 Jul 2004 (UTC)

Since you didn't respond, I'm erasing this. Gadykozma 07:26, 3 Aug 2004 (UTC)

I've restored the comment that you erased, but I've weakened it a bit so that it says only as much as is known to everyone who's read a bit about the history of Cantor's theory. For all I know it may be right, but it's been a long time since I've read anything specific. Michael Hardy 16:03, 3 Aug 2004 (UTC)

I edited it again, because

• The Cantor set is not "extremely abstract". A strongly inaccessible cardinal is abstract. A functor on sheaf categories is abstract. The Cantor set is a simple, well defined set, for which it is normally easy to check if a specific point is in or not.
• "particular" implies that he had a specific series in mind, which I seriously doubt.
• I still doubt that he was interested in Fourier series. As a kind of compromise I changed it to "trignometric series" which is ambiguous, it can refer to either Fourier series or uniqueness problems. But it still links to Fourier series, I didn't change it to link to set of uniqueness or something. I would still like if somebody could check this point in a history book. Or maybe just to unlink it until we are sure?

Michael, are you OK with this? Gadykozma 07:03, 4 Aug 2004 (UTC)

For now, yes. Maybe I'll add some things later if I look up specifics that I haven't read about for a long time. Michael Hardy 15:02, 16 Aug 2004 (UTC)

I changed "named after" to "invented by", since that information is not otherwise given until the end of the article. "named after its inventor" might even be better, but with "German mathematician" it gets wordy. --anon

How about "discovered" rather than "invented"? Gadykozma 21:36, 24 Sep 2004 (UTC)

Notes on Rewrite, May 2005

Just logging what I have done here. There were a few problems with the page, which I started fixing and then got carried away. The overall structure is unchanged, but paras have been rewritten for clarity, completeness and/or correctness. Summary:

• Prose was "you do this", "if you add up" and the like. I hope my rewrite is more encyclopædic
• Uncountability: this section went straight into discussion of ternary characterisation of C - I added a preliminary statement as to why you would want to do this.
• Characterisation of set in ternary: made links between ternary construction and existing material on numerals, including illustrative examples.
• Mapping from C to [0,1]: it wasn't explicit that this function is well-defined and onto. It now is. I also note that it is not 1-1.
• For nowhere dense, the property proven doesn't quite align with the definition in nowhere dense - fixed.
• Totally disconnected doesn't follow from nowhere dense in general. (TD is a property of a top space in itself, whereas nowhere dense requires a superset space.)
• added a note that the "middle 80%" version works nicely with decimals

These changes will obviously need some third-party input, or mass-reversion, or whatever. IMHO now, today, this minute, I have probably improved it, but I may think differently on re-reading it. Andrew Kepert 08:40, 4 May 2005 (UTC)

Null set

the page on null set says the cantor set is a null set. This should be notied if true. Fresheneesz 22:02, 3 March 2006 (UTC)

The middle-third construction gives a set with measure zero; any set with measure zero is a null set. However, other constructions, e.g. the Smith-Volterra-Cantor set, is not a null set; you can build Cantor sets with any measure. For example, if you remove the rationals from the reals, you get a set that is is homeomorphic to the Cantor set but has measure one. linas 22:59, 3 March 2006 (UTC)

The Cantor set is compact, the set of all irrationals is not compact. So they cannot be homeomorphic. -- Leocat 20:07, 1 November 2006 (UTC)

Irrational numbers in the Cantor set

The article stated that "the remaining points [in the Cantor set] are all numbers of the form k/3ⁿ such that n is a positive integer and k/3ⁿ does not lie in any middle third (in other words, k/3ⁿ is in the Cantor set if and only if it is an endpoint of some interval for the nth iteration)." These points, clearly, are all rational numbers--but while Q is countable, the Cantor set is uncountable. So there are (uncountably many) numbers in the Cantor set that are not in Q--and thus not of the form k/3^n. (Unfortunately, I don't know of a way to construct one of these points.) I have removed this claim.

Dzhim 18:18, 28 March 2006 (UTC)

Its also incorrect to say that the "intervals shrink to points" -- they don't, they remain intervals. linas 00:39, 29 March 2006 (UTC)

To answer my own question: 1/4 = 0.020202...₃ is in the Cantor set, but clearly it's not an endpoint of any interval in any (finite) iteration. (1/4 is rational, of course, but it's easy to see how an irrational number could be similarly constructed: for example, 0.220200200020000...₃.) This example of 1/4 was mentioned in an earlier version of this article, but it was muddled and misstated (at least one version said "1/3" instead of "1/4"). Similarly, the Cantor set's inclusion of 7/10 is mentioned briefly, later in the article. Since it's somewhat surprising that the Cantor set includes points besides those endpoints (and a common misconception that it doesn't), I think it's important that we mention it more explicitly and explain how these "extra" points made it into the Cantor set. --Dzhim 18:56, 30 March 2006 (UTC)

I agree with your last statements, although I am not sure how to best explain it. Your words are slightly misleading: explain how these "extra" points made it into...: on the contrary, they were never removed; the construction did not remove them. Furthermore, there are uncountably many of these interior points, whereas the boundry points are countable.

I think the whole topic can be incredibly confusing if the reader has no background in topology. One can, for example, have finer topologies on the real numbers, and these other topologies are "worse" and have weirder weirdneses. This is why the standard topology is popular. This article would probably benefit from a review of general topology, because merely applying "naive intuition" to the Cantor set can lead one into trouble. linas 20:05, 30 March 2006 (UTC)

Hi, everybody, I'd like you to consider what exactly are ternary representations of the Cantor set points. Let C_n denote the n-th approximation of the Cantor set.

• Initially, we have an interval C₀=[0,1], that is numbers beginning whith zero: 0.... plus the ending one: 1.
• In the first step we delete the (1/3,2/3) interval, so we remove all numbers with digit 1 at the first fraction place, that is numbers 0.1... — except 0.1=1/3 itself. So C₁ contains all numbers but those with 1 at 1-st place — except 0.1 which belongs to C₁.
• In the second step we remove numbers, which have digit 1 at 2-nd fraction place, except 0.01 (1/9) and 0.21 (7/9), which are right ends of two sub-intervals. So C₂ contains all numbers which do not have a 1 digit on first two fraction places, plus {0.01, 0.1, 0.21}, which end with a 1 at one of those places.
• And so on...

Finally the Cantor set C_∞ contains all numbers, which do not have digit 1 in their ternary representation or have exactly one 1 digit, and it is their last non-zero digit. One might describe the possible ternary representations with a string regular expression like this:

0(dot)[02]* | 0(dot)[02]*10* | 1(dot)0*

First part describes all strings wih no 1's, the next one allows finite strings ending with 1 (after which only zeros are accepted), the last part describes the biggest, rightmost point of the set.

Now it is obvious, that Cantor set in uncountable, because its subset is same cardinality as the [0,1] interval. To proove it replace digit 2 with 1 in the first part of regular expression above, and you get all infinite binary strings, which gives an injection of the interval into the Cantor set.

It also becomes obvious, that some irrational numbers belong to the set. Those are of course all numbers given with infinite, non-periodic ternary representations, built solely with digits 0 and 2. It's not so obvious, however, how to express any of those numbers in other systems, eg. binary, decimal, or with an algebraic expression.

CiaPan 19:29, 21 April 2006 (UTC)

Is it possible to say that all irrational numbers in the Cantor set are transcendent? I have this intuitive idea that algebraic irrational numbers represented in any basis should look like a random sequence of digits, and Cantor set elements in base 3 would lack number 1. Albmont 19:37, 23 March 2007 (UTC)

The Cantor set contains no intervals

I deleted ths section, as the proof was inadequate. But I think the point is worth making, so I used it to introduce the paragraph showing that the Cantor set is non-empty, without giving a complete proof. (One could give a proof without any measure theory by showing that if I is an interval of non-zero length then it must contain an end point of one of the intervals removed in the construction. But this seemed a bit fiddly to put right at the start.)

• Well, the Cantor set clearly contais 1 and 0. !!!

References

Corrected the reference to Cantor's original paper in Acta Mathematica. Canter 21:23, 16 October 2006 (UTC)

This link is obsolete

"http://swiki.hfbk-hamburg.de:8888/MusicTechnology/799" Should this be removed or updated? Azotlichid, 18 November 2006

Fractals with continous curves?

In the article: "The Cantor set is the prototype of a fractal." Am I right in thinking that most examples (Mandelbrot, etc.) of fractals are continous and that a Cantor set isn't? This would be a useful consideration to anyone studying fractals. JWhiteheadcc 11:31, 12 November 2007 (UTC)

Method to generate arbitary sets

Using the idea of an arbitary base with one value disallowed for all digits, it is possible to just create an infinite number of sets.

Examples in base-10 (decimal), disallowing 1: 0.023495967029=in the set 0.2121=not in the set 1/9th=0.11111...=not in the set 1/8th=0.125=in the set Note that 'the set' is to be taken in context as being the set I just defined.

In general, for a base-n set, there are a finite number of sets possible to construct this way. For decimal, I believe there is 9+9*8+8*7*6+7*6*5*4+6*5*4*3*2 possible solutions. It might be something else but I'm too tired to double check this. Please verify. If instead of a recursion, each cycle uses a different disallowed digit, then there's an infinite number of decimal sets.

I'm wondering if any of this would be useful to add to the encyclopedia. JWhiteheadcc 11:46, 12 November 2007 (UTC)

Looking at the sets generated by removing different digits or different groups of digits is a nice idea for some recreational research. I can think of several interesting questions that would be fun to think about. But I don't think it needs to be in the article, since these various constructions have not yet proven to be of general interest in the areas of mathematics where Cantor sets are commonly studied. — Carl (CBM · talk) 13:18, 12 November 2007 (UTC)

The number of solutions is factorial according to my calculations. Technically they are just numerical representations of Cantor Sets. The base-3 set is just the most famous. It would probably be redundant though, to add them, since the general idea is the same. —Preceding unsigned comment added by JWhiteheadcc (talk • contribs) 20:59, 12 November 2007 (UTC)

What's In The Cantor Set?

This section mentions the Cantor Set is finite. I'd say it's COUNTABLY finite. Wondering whether to edit this section to add that detail. Might be TMI. :-) Martin Packer (talk) 14:55, 10 December 2007 (UTC)

It's not finite and it's not countably infinite; it's uncountably infinite. Michael Hardy (talk) 16:22, 10 December 2007 (UTC)

Where do you find anything like that in that section? I don't see anything that says the Cantor set is finite; I'd have corrected it if I had. And: "countably finite" is a redundancy. There is a difference between countably infinite and uncountably infinite, but all finite sets are countable. Michael Hardy (talk) 16:28, 10 December 2007 (UTC)

Oh crap! That's what comes of typing tired... I meant INfinite and Countably INfinite. I do think Countably Infinite is justifiable and a useful thing to say. So I stand (gently) corrected - in my typo's. But should we edit to add the word "Countably"? Martin Packer (talk) 19:50, 10 December 2007 (UTC)

The Cantor set is not countably infinite. It has the same cardinality as the set of real numbers. — Carl (CBM · talk) 20:28, 10 December 2007 (UTC)

If you think it's countably infinite, you haven't read the article carefully enough. Michael Hardy (talk) 20:55, 10 December 2007 (UTC)

Variations of the Cantor Set

It's been a while since I have thought about this, but I am pretty sure if you take out less than 1/3 of each segment, you end up with a set of nonzero measure. It's a simple geometric series; I don't have time now to go through it but maybe I will add that some other time if no one else is interested. Uranographer (talk) 01:06, 8 March 2008 (UTC)

• Well, let's try it with fraction 1/4. Let's define our set as "The set of numbers from interval [0,1] whose base-4 representation does not contain the digit 1. So let's first remove numbers which contain the digit 1 at the first position. This removes 1/4 of the full interval and leaves 3 subintervals (for the first digit being 0, 2, or 3). Now let's remove numbers which contain the digit 1 at the second position. Again, this removes one quarter of each subinterval, and so on. When we look at the progression of measures of the partially constructed sets, we get 3/4, (3/4)^2, (3/4)^3 and so on; the limit of this sequence is 0. Finally, the finished set is a subset of each partial set, so it has measure 0. - Mike Rosoft (talk) 21:16, 23 October 2017 (UTC)
• It is not necessary to always take the middle interval, either. For example, take the set of numbers whose base-3 representation does not contain the digit 0. It can be seen that this set still has measure 0 (though the construction is not as symmetric as the original Cantor set). - Mike Rosoft (talk) 21:16, 23 October 2017 (UTC)

"What's in the Cantor Set?" sum equation is wrong

The equation for the series sum is given incorrectly as (1/3)*(1-2/3) = 1 ... (1/3)*(1-2/3)=1/9 which is not the sum of the gaps. The series sum equation should be (1/3)/(1-2/3) = 1. I have no idea how to show that via math markup, I noodled around but kept getting parsing errors. Thanks! - goatasaur (talk) 16:04, 25 April 2008 (UTC)

Rough fix, markup looks a little weird but at least the equation is right. -- goatasaur (talk) 08:57, 27 April 2008 (UTC)

I was wrong, the equation reads 1/3 * 1/(1/3) which is equal to one. Oops. -- goatasaur (talk) 15:55, 28 April 2008 (UTC)

Layman question

Are 0 and 1 in this set? 118.90.35.242 (talk) 19:42, 12 October 2008 (UTC)

Yes. — Carl (CBM · talk) 19:54, 12 October 2008 (UTC)

• We could easily define the set to exclude the endpoints of each interval (like 0, 1, 1/3, 2/3, ...) By doing this, we would get not "a set of numbers on closed interval [0,1] which have a base-3 representation not containing the digit 1" (the original Cantor set), but rather "a set of numbers on open interval (0,1) which do not have a base-3 representation containing the digit 1". (I am not sure why does the original definition use the convention that the endpoints of intervals are included rather than excluded; in any case, all endpoints are rational numbers, so by excluding them we get a set that differs from the original by countably many members; so the restricted set is still uncountable and has measure zero.)
  • I am going to answer myself: the reason why the endpoints are included rather than excluded are probably its topological properties, so that the resulting set is closed and perfect. - Mike Rosoft (talk) 06:57, 28 October 2017 (UTC)

Self-similarity

The relation currently given here is true for pretty much any set of points on the real line. What is needed here is that $f_{L}(C)\cong f_{R}(C)\cong C=f_{L}(C)\cup f_{R}(C)$

Which crucially states that the union of the left and right transformations is precisely the Cantor set.81.134.83.6 (talk) 16:18, 28 February 2018 (UTC)

I feel a little out of my depth, but I believe the following equation in the Self-similarity section is wrong. $f_{L}(C)=f_{R}(C)=C$ should be $f_{L}(C)\cup f_{R}(C)=C$. SamIAmNot (talk) 20:09, 14 October 2008 (UTC)

You're raising a good point. You're right that $f_{L}(C)\cup f_{R}(C)=C$ but I think that what was actually intended was something like $f_{L}(C)\cong f_{R}(C)\cong C$. I would change it but I'm not sure what's the best way to explain the strong sense in which the sets are homeomorphic. — Carl (CBM · talk) 23:59, 14 October 2008 (UTC)

Irrational numbers

obviously the cantor set will contain irrational numbers, but it seems only the end points are left. can some1 gimme an example? cuz i dunno how 2 prove there is one —Preceding unsigned comment added by Cheat notes (talk • contribs) 12:24, 14 January 2009 (UTC) oh btw, how is it nowhere dense? it's dense in itself isnt it? i mean since its perf every point in it is a limit point, so cantor set S is dense in S... —Preceding unsigned comment added by Cheat notes (talk • contribs) 12:30, 14 January 2009 (UTC)

Nowhere dense means not dense in any open set. Every set is dense in itself. — Carl (CBM · talk) 03:27, 4 March 2009 (UTC)

• Cantor set is the set of numbers on [0,1] whose base-3 expansion does not contain the digit 1. For example, it contains the following number in base-3: 0.202002000200002... - Mike Rosoft (talk) 07:03, 28 October 2017 (UTC)

Practical applications

I would love to see a section in this article which discusses applications if there are any. See the article on eigenvalues and eigenvectors for a really good example of what I'm talking about. I know this is an important topic without applications, I just think it makes math more accessible to us left-brainers. 4.249.3.9 (talk) 21:30, 2 July 2009 (UTC)

Unsatisfactory proof

In the paragraph "Cardinality" it is stated:

1/3 = 0.13 = 0.022222...3 (This alternative recurring representation of a number with a terminating numeral occurs in any positional system.)

Let's for simplicity work in decimal system; Similar of the above statement in decimal system would be: 1 = 0.99999999...

Now the problem: what does 0.9999999... mean? In mathematics we can not work with an object unless we define it first. If we define 0.999999.. to be the limit of 0.9+0.09+0.009+... (which is equal to 1) then 0.999999.. is 1 by definition, but then we are not allowed to do the (arbitrary) manipulation with the digits as is done in the presented proof

To clarify, this is because by this definition "0.99999..." is just a different way to write 1, as is the word "one" and the digits in "0.999999..." are NOT digits in the mathematical sense anymore, but just like letters in a word

We can not just say that "0.999999.." is the real number that when written in decimal system has has a zero, a point and infinitely many nines. This is NOT a valid (rigorous) definition of a number. If we say it has (for example) one million nines, then it will be ok. But we don't know what it means to write "infinitely many" nines. For this purpose they invented the infinitesimal calculus a few centuries ago so we can do these things right. Then again, as i said, if we take the limit of a sequence, it wont work in this case.

I sincerely suspect this proof to be fundamentally invalid and can't be made valid with minor corrections or additions though i can be wrong for this.

Now that i think of it i even doubt that there is a bijection between the cantor set and the interval [0,1] (and so both cardinalities are equal). It both goes against my intuition and lacks a (valid) proof (at least i know of no such proof).

—Preceding unsigned comment added by 213.240.234.31 (talk) 15:28, 11 December 2009 (UTC)

I have read the above post several times to try to work out what the problem is, so that I can help to clarify the issue. However, it is very unclear, and I am not really sure what the misunderstanding is. The crux of the matter appears to be "we are not allowed to do the (arbitrary) manipulation with the digits as is done in the presented proof". What is arbitrary about it? Why are we not allowed to do it? Then we are told that "0.999999.." "is NOT a valid (rigorous) definition of a number". Why not? It means the number which is the limit of the geometric series 0.9 + 0.09 + 0.009 + ..., as the same post had previously stated: there is nothing invalid about that. JamesBWatson (talk) 10:39, 23 December 2009 (UTC)

I duscussed about 2 possible ways to define the 0.99999... and explained what are the (different) problems in both cases:

a) if we define it to be the limit of 0.9 + 0.09... then this is just 1. Then we effectively define 0.9999... := 1. As i said the digits then bear no meaning. We could as well define 0.777777... := 1. That does not give us the liberty to do with the digits 777.. anything. I hope this time i managed to explain what i had in mind. What other example to give. Lets say you define o := 1 (where "o" is the letter and not the digit zero) then we take the liberty to treat the letter "o" as the digit "0" just because there is a visual resemblance. And then we get to 1 = 0.

b) the second way to define it is "the real number which when written in decimal system has a zero, a point and infinitely many nines." Now this is not valid because it is simply impossible to write infinitely many nines. Now you may say that this (infinite) writting is not actual physical writting but only imagenary. Ok but then we don't know what will be result of that imagenary procedure. In particular we cant know that it will be the number 1. Now it may seem intuitive, but i still say this is mathematics and a proposition is considered to be true only after a rigorous proof. And i dont see how we can apply any formal thinking about an informally described imaginary procedure, let alone to prove that it will result in something partiular.—Preceding unsigned comment added by 87.121.84.214 (talk) 20:04, 26 December 2009 (UTC)

• The answer is that the options a and b are equivalent by definition; that is, the number 0.999..., i.e. the number with a nine at every decimal position after the decimal point, is by definition equal to the infinite sum 0.9+0.09+0.009+... And the infinite sum is the limit of the sequence of partial sums: 0.9, 0.99, 0.999...; and the limit happens to be equal to 1. (For the same reason, the number 0.111... is equal to 1/9.) See 0.999.... - Mike Rosoft (talk) 20:45, 23 October 2017 (UTC)

is it appropriate to add that it's a perfect subset of R, uncountable, it is a zero set ?

zero set proof is pretty simple but some others would have to be shown as corollaries. i'm new at adding things to math articles that require computation symbols, how would go about adding them ?Grmike (talk) 03:24, 7 February 2010 (UTC)grmike

Proof regarding cardinality & the AC

The current proof in the article that $|C|=\aleph$ uses the axiom of choice (by saying that $f$ maps C onto $[0,1]\Rightarrow |C|\geq \aleph$). I'm pretty sure that it is not necessary. For example, a bijection between C and the set of infinite binary sequences could be constructed by
$f(x):=(.\alpha _{1}\alpha _{2}\alpha _{3}\dots )_{2}$
where $\alpha _{n}=1$ whenever $x$ is to the right of the interval that was removed (in the n^th step of the construction of C) from the interval $x$ is in.

I personally feel that the AC should be avoided whenever possible. What do you guys think?Dlivnat (talk) 20:34, 4 March 2010 (UTC)

I agree with you that a proof without AC, where it can be avoided, is more elegant than one with it.

I'm not sure what proof you're referring to, though, because $\aleph$ by itself doesn't have any standard meaning. $\aleph _{0}$ does have a meaning: It is the cardinality of the integers (or equivalently, of the positive integers). It is known that the cardinality of the Cantor set C is $|C|=2^{\aleph _{0}}$. :Put another way, |C| = |${\mathcal {P}}$(ℤ)|, the cardinality of the power set of the integers, or equivalently of the power set of the positive integers.

The best way to prove this is to just show that the Cantor set is in one-to-one correspondence with a countable sequence of binary choices. (The Cantor set is in fact not only in bijective correspondence with such a sequence, but it is even topologically equivalent to the countable direct product of the discrete space of two points.)But it is unknown, and some would say unknowable, where the cardinal number $c=2^{\aleph _{0}}$ fits into the sequence of cardinal numbers. (It must be $\aleph _{\psi }$ for some ordinal $\psi$ that must satisfy 1 <= ψ <= |C| and $\psi \neq \omega$. (Where $\omega$ is the least infinite ordinal, i.e., that of the natural numbers; and where the cardinal |C| is represented by the least ordinal having its cardinality.) So it is even possible that $\psi =2^{\aleph _{0}}$, or in other words that $2^{\aleph _{0}}=\aleph _{2^{\aleph _{0}}}$.Daqu (talk) 19:14, 24 September 2014 (UTC)

Reference Unnecessary?

In the proof that the Cantor Set is uncountable, it says that:

To see this, we show that there is a function f from the Cantor set C to the closed interval [0,1] that is surjective (i.e. f maps from C onto [0,1]) so that the cardinality of C is no less than that of [0,1]. Since C is a subset of [0,1], its cardinality is also no greater, so the two cardinalities must in fact be equal, by the Cantor–Bernstein–Schroeder theorem.

However, I don't see why it is necessary to bring up the Cantor-Bernstein-Schroeder theorem. If the Cantor Set's cardinality is greater than or equal to the cardinality of [0,1] and also less than or equal to it, then it follows that they are equal. If the theorem isn't directly related here, then maybe it should be removed or the reference should be moved somewhere else. — Preceding unsigned comment added by 68.49.92.23 (talk) 22:35, 10 July 2012 (UTC)

The Cantor-Bernstein-Schroeder theorem is the simplest way to take the mathematical meaning of the statements that $\gamma \leq \delta$ and $\delta \leq \gamma$ and to conclude that $\gamma =\delta$ (for cardinals $\gamma$ and $\delta$). Of course, once this theorem is proved, it doesn't need to be proved again.Daqu (talk) 19:21, 24 September 2014 (UTC)

Explicit formula

Firstly, I'm just a boy interested in maths, so bear with me if i am wrong. But:

I think the first explicit formula of the set is wrong. I think that instead of $\lim _{m\to \infty }$, there should be a $\bigcap _{m=1}^{\infty }.$

If you agree, I think someone should change it! Otherwise, please correct me. — Preceding unsigned comment added by 188.183.128.99 (talk) 20:04, 25 May 2013 (UTC)

You are not wrong, but $\lim _{n}$ is acceptable because the sequence of sets is monotone, so it is convergent in some sense: if one associates to each set A_n in the sequence the function f_n equal to 1 on the set A_n and to 0 outside, then f_n(x) converges for every real x to a value f(x) equal to 1 on the "limit set" and 0 outside. Bdmy (talk) 22:50, 25 May 2013 (UTC)

Well, I was wrong. The sequence of sets in the article is not monotone, and the formula is really wrong. Bdmy (talk) 23:23, 25 May 2013 (UTC)

Massively false statement

The section Topological and analytical properties contains this statment:

"One can see that Γ is totally disconnected and perfect - thus it is homeomorphic to the Cantor set."

This is very false.

For example, a countable disjoint union of Cantor sets is also totally disconnected and perfect, but not compact.

Another example is 2^(2N). (I.e., the cartesian product of continuum-many copies of the set {0,1} with its discrete topology.) This space is even compact, as well as totally disconnected and perfect — but not homeomorphic to the Cantor set.

Even though I know why the space in question is homeomorphic to the Cantor set, the sentence quoted does not explain it.Daqu (talk) 02:49, 7 September 2014 (UTC)

Statement makes no sense

The section Construction and formula of the ternary set contains this passage (with the formula omitted):

"Let us note that this description of the Cantor set does not characterize the complement of the Cantor set exactly, since the sets given by the formula [here an explicit formula is given] are not disjoint."

This is nonsense, since the formula given is an explicit formula for the complement of the Cantor set. Thus it characterizes the complement of the Cantor set exactly.

If someone wants to describe the complement as the disjoint union of open intervals, that is fine. But the statement is nonsense.Daqu (talk) 03:07, 7 September 2014 (UTC)

Confusing statements

The last paragraph in the section Topological and analytical properties contains this passage:

"For any integer q ≥ 2, the topology on the group G=Z_q^ω (the countable direct sum) is discrete. Although the Pontrjagin dual Γ is also Z_q^ω, the topology of Γ is compact. "

But since the notation Z_q is used for more than one thing in mathematics, the meaning of Z_q here needs to be specified.

It seems that the intention is not the finite cyclic group Z/qZ, because in that case the countable direct sum of copies of this group is only countable, but its Pontrjagin dual is uncountable.

If on the other hand, the meaning of Z_q is the q-adic integers (the only other meaning of Z_q that I am familiar with), then this statement seems wrong, also — and in any case, "q-adic integers" makes sense only if q is a prime number — which is clearly is not specified to be.

Also: What does it *mean* where it states:

"the Pontrjagin dual Γ is also Z_q^ω "

??? Whatever the intended meaning of Z_q^ω, it is a topological group and for that reason it is unclear what the meaning of "is" is.Daqu (talk) 16:42, 1 March 2016 (UTC)

Interesting extension of the Cantor set

Recall that the Cantor set is the set of numbers from interval from 0 to 1 whose base-3 representation does not contain the digit 1. Let's extend it to a set of numbers which contain finitely many digits 1. Start with the Cantor set; note that the set omits the central interval representing numbers which contain the digit 1 at the first position. Let's now allow this interval, as long as the number does not contain any more digits 1; this replaces the omitted interval with a scaled down Cantor set. Now we have three intervals (for numbers with digit 0, 1, or 2 at position 1), each omitting the central subinterval (digit 1 at position 2), which we replace with a scaled down copy of the Cantor set (no more digits 1). Now we have nine intervals (all possible digits at positions 1 and 2), each with an omitted central subinterval which we replace with a scaled sown copy of the Cantor set, etc.

What we get is:

• At layer 0 the Cantor set. (The set of numbers which does not contain the digit 1.)
• At layer 1 one scaled down copy of the Cantor set. (The set of numbers whose last appearance of the digit 1 is at position 1.)
• At layer 2 three copies of the Cantor set. (The set of numbers whose last appearance of the digit 1 is at position 2.)
• At layer 3 nine copies. (Last digit 1 at position 3.)
• At layer 4 ...

So altogether at each layer there are finitely many sets of measure zero, so each layer has itself measure zero. And a union of countably many layers of measure zero still has measure zero. We have now gotten an uncountable, dense subset of interval from 0 to 1 of measure zero.

(Does this set have a name? What are its topological properties?) - Mike Rosoft (talk) 20:56, 24 October 2017 (UTC)

Suggestions for "Properties" section

The section with all the properties of the Cantor set would be a lot more readable, if each property were listed before its proof rather than after its proof. --345Kai (talk) 19:33, 2 May 2018 (UTC)

Omission

There should be a section here, noting that some deny the existence of the Cantor set altogether. — Preceding unsigned comment added by 2A00:23C0:FCF6:4801:C43C:4F7C:53E0:BB3 (talk) 07:15, 4 June 2018 (UTC)

The article mentions six steps. It is much easier to illustrate six steps than it is to illustrate an infinite number of steps.

The Cantor cubes only show about six stages, six being a finite number. — Preceding unsigned comment added by 2A00:23C0:FCF6:4801:C43C:4F7C:53E0:BB3 (talk) 07:07, 5 June 2018 (UTC)

repeating fraction with a repetend that uses only

I. The sentence in question:

>In arithmetical terms, the Cantor set consists of all real numbers of the unit interval that are expressible as a ternary fraction using only the digits 0 and 2.

You’re trying to say we don’t NEED the digit 1 to express the full set. But the way it's written is poorly conceived and ambiguous. Yes, the numbers CAN all be expressed with 0s and 2s, but they’re not ONLY expressible with 0s and 2s. An infinite amount can ALSO be expressed using the digit 1. Using whimsical notation to express the set with only 0s and 2s is a choice, not a limit of the set, and it’s certainly not an “arithmetical term.”

The following is just as true, ambiguous, and whimsical:

>In arithmetical terms, the set of 3 digit numbers that alternate between 1 and 3 (131, 313) consists of all integers that are expressible as a quaternary sum using only each digit to the power of itself.

As it stands, the sentence only serves to call attention to its own awkwardness and should be rewritten for clarity.

II. From your comment below:

" Its ternary contains only 0s and 2s, but neither the 0 nor the 2 is the repetend. "

This is irrelevant. The point is that the repeating part can only consist of 0s and 2s, but that the non repeating part can also consist of 1s. It has nothing to do with whether the period is equal to or greater than 1.

2604:2000:81CF:2B00:A1AD:998B:217B:9B39 (talk) 13:01, 21 January 2019 (UTC) >>>

No, you are not right.
All finite or infinite representations consisting only of 0s and 2s belong to the Cantor set. These are more than those with repetends 0 or 2. E.g. $1/4=2\cdot 3^{-2}+2\cdot 3^{-4}+2\cdot 3^{-6}+\cdots =0{,}{\overline {02}}_{3}$ belongs to the Cantor set. Its ternary contains only 0s and 2s, but neither the 0 nor the 2 is the repetend.
Note: With repeating groups you only get rational numbers, and you know those are countable. But the Cantor set is uncountable, so there are uncountably many non-repeating ternaries consisting only of 0s and 2s. --Nomen4Omen (talk) 19:59, 20 January 2019 (UTC)

Please explain the mapping to binary sequences

Is it?

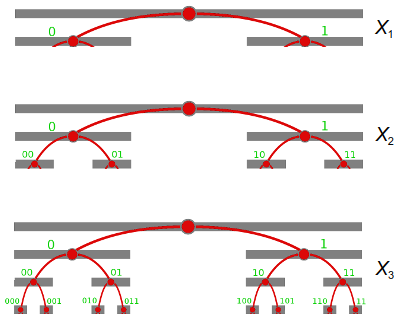
X1 = {0, 1}; X2 = {0, 00, 01, 1, 10, 11}; X3 = {0, 00, 000, 001, 01, 010, 011, ..., 111}; Xk = ...;

In usual applications the set X_k is the domain of a set of identifiers (or indexes), and k is finite.

There are an intuitive recursive construction rule (illustrated) for each new X_k after X₁

X_k  = P_k U X_k-1

where P_k is the set of all of 2^k numbers expressed as fixed-length (k) bit strings. Example:

X₂  = P₂ U X₁  = {00, 01, 10, 11} U {0, 1}.

The number of elements, |X_k|, after |X₁|=2, is the recurrence

|X_k| = |X_k-1| + 2^k.  

Examples of |X_k| for k ranging from 2 to 8:

|X₂| = 2+4=6;   |X₃| = 6+8=14;   |X₄| = 14+16=30;   ...; |X₈| = 254+256=510.

PS: by induction we see that |X_k| = 2^k+1-2.

Krauss (talk) 11:04, 17 March 2019 (UTC)

Please add hierarchical tree of the Cantor set

The Cantor Set is not only a mathematical abstraction to demonstrate "the infinite", but also a classical model and perhaps the simplest fractal with a complete and consensual documentation. As real-world Cantor Set (a linear Cantor dust produced by light) see e.g. ref1 or ref2.

Because of finite size of the real-world fractal structures, the correct model is the finite Cantor set.

And perhaps the most didactic and most used abstraction, it is not the Cantor set! The ref1 named it "hierarchical tree of the Cantor set". The tree T_k use the constructor C_k in a different way... Instead of intersection the hierarchy is an union: $T_{k}=\bigcup _{m=1}^{k}C_{m}$. We can show also that $|T_{k}|=|T_{k-1}|+2^{k}=2^{k+1}-2$.

All concepts, the finite Cantor set and the hierarchical tree of the finite Cantor set are encyclopedic. It is important to introduce it in the article. Krauss (talk) 16:55, 24 March 2019 (UTC)

Unclear paragraph

The next-to-last paragraph in the section Topological and analytical properties reads as follows:

"For any integer q ≥ 2, the topology on the group G=Zq^ω (the countable direct sum) is discrete. Although the Pontrjagin dual Γ is also Zq^ω, the topology of Γ is compact. One can see that Γ is totally disconnected and perfect - thus it is homeomorphic to the Cantor set. It is easiest to write out the homeomorphism explicitly in the case q=2. (See Rudin 1962 p 40.)"

Can we assume that Z_q denotes the group of integers modulo q ???

If so, why are we concerned with the "countable direct sum" of this group with itself???

That is not the Cantor set (the direct sum is only countable), so: What is the connection?

Or perhaps Z_q instead denotes the q-adic integers???

Clarification is needed here.47.44.96.195 (talk) 15:14, 28 October 2020 (UTC)