5-cell

Regular 5-cell
(pentachoron)
(4-simplex)
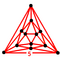
Regular 5-cell; (pentachoron); (4-simplex)
	Schlegel diagram; (vertices and edges)
Type	Convex regular 4-polytope
Schläfli symbol	{3,3,3}
Coxeter diagram
Cells	5 {3,3}
Faces	10 {3}
Edges	10
Vertices	5
Vertex figure	; (tetrahedron)
Petrie polygon	pentagon
Coxeter group	A4, [3,3,3]
Dual	Self-dual
Properties	convex, isogonal, isotoxal, isohedral
Uniform index	1

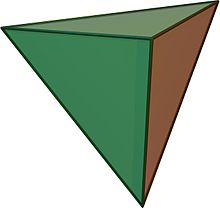
In geometry, the 5-cell is a four-dimensional object bounded by 5 tetrahedral cells. It is also known as a C₅, pentachoron,^[1] pentatope, pentahedroid,^[2] or tetrahedral pyramid. It is the 4-simplex (Coxeter's $\alpha _{4}$ polytope^[3]), the simplest possible convex regular 4-polytope (four-dimensional analogue of a Platonic solid), and is analogous to the tetrahedron in three dimensions and the triangle in two dimensions. The pentachoron is a four dimensional pyramid with a tetrahedral base.

The regular 5-cell is bounded by 5 regular tetrahedra, and is one of the six regular convex 4-polytopes, represented by the Schläfli symbol {3,3,3}.

The 5-cell is a solution to the problem: Make 10 equilateral triangles, all of the same size, using 10 matchsticks, where each side of every triangle is exactly one matchstick. No solution exists in three dimensions.

The convex hull of the 5-cell and its dual (assuming that they are congruent) is the disphenoidal 30-cell, dual of the bitruncated 5-cell.

Alternative names

Pentachoron
4-simplex
Pentatope
Pentahedroid (Henry Parker Manning)
Pen (Jonathan Bowers: for pentachoron)^[4]
Hyperpyramid, tetrahedral pyramid

Geometry

The 5-cell is self-dual, and its vertex figure is a tetrahedron. Its maximal intersection with 3-dimensional space is the triangular prism. Its dihedral angle is cos⁻¹(⁠1/4⁠), or approximately 75.52°.

As a configuration

This configuration matrix represents the 5-cell. The rows and columns correspond to vertices, edges, faces, and cells. The diagonal numbers say how many of each element occur in the whole 5-cell. The nondiagonal numbers say how many of the column's element occur in or at the row's element. This self-dual polytope's matrix is identical to its 180 degree rotation.^[5]

${\begin{bmatrix}{\begin{matrix}5&4&6&4\\2&10&3&3\\3&3&10&2\\4&6&4&5\end{matrix}}\end{bmatrix}}$

Construction

The 5-cell can be constructed from a tetrahedron by adding a 5th vertex such that it is equidistant from all the other vertices of the tetrahedron. (The 5-cell is a 4-dimensional pyramid with a tetrahedral base and four tetrahedral sides.)

The simplest set of coordinates is: (2,0,0,0), (0,2,0,0), (0,0,2,0), (0,0,0,2), (φ,φ,φ,φ), with edge length 2√2, where φ is the golden ratio.^[6]

The Cartesian coordinates of the vertices of an origin-centered regular 5-cell having edge length 2 are:

\left({\frac {1}{\sqrt {10}}},\ {\frac {1}{\sqrt {6}}},\ {\frac {1}{\sqrt {3}}},\ \pm 1\right)

\left({\frac {1}{\sqrt {10}}},\ {\frac {1}{\sqrt {6}}},\ {\frac {-2}{\sqrt {3}}},\ 0\right)

\left({\frac {1}{\sqrt {10}}},\ -{\sqrt {\frac {3}{2}}},\ 0,\ 0\right)

\left(-2{\sqrt {\frac {2}{5}}},\ 0,\ 0,\ 0\right)

Another set of origin-centered coordinates in 4-space can be seen as a hyperpyramid with a regular tetrahedral base in 3-space, with edge length 2√2:

\left(1,1,1,{\frac {-1}{\sqrt {5}}}\right)

\left(1,-1,-1,{\frac {-1}{\sqrt {5}}}\right)

\left(-1,1,-1,{\frac {-1}{\sqrt {5}}}\right)

\left(-1,-1,1,{\frac {-1}{\sqrt {5}}}\right)

\left(0,0,0,{\frac {4}{\sqrt {5}}}\right)

The vertices of a 4-simplex (with edge √2) can be more simply constructed on a hyperplane in 5-space, as (distinct) permutations of (0,0,0,0,1) or (0,1,1,1,1); in these positions it is a facet of, respectively, the 5-orthoplex or the rectified penteract.

Boerdijk–Coxeter helix

A 5-cell can be constructed as a Boerdijk–Coxeter helix of five chained tetrahedra, folded into a 4-dimensional ring. The 10 triangle faces can be seen in a 2D net within a triangular tiling, with 6 triangles around every vertex, although folding into 4-dimensions causes edges to coincide. The purple edges represent the Petrie polygon of the 5-cell.

Projections

The A₄ Coxeter plane projects the 5-cell into a regular pentagon and pentagram.

orthographic projections
A_k Coxeter plane	A₄	A₃	A₂
Graph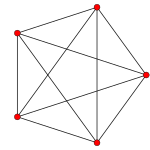
Dihedral symmetry	[5]	[4]	[3]

Projections to 3 dimensions
Stereographic projection wireframe (edge projected onto a 3-sphere)	A 3D projection of a 5-cell performing a simple rotation
The vertex-first projection of the 5-cell into 3 dimensions has a tetrahedral projection envelope. The closest vertex of the 5-cell projects to the center of the tetrahedron, as shown here in red. The farthest cell projects onto the tetrahedral envelope itself, while the other 4 cells project onto the 4 flattened tetrahedral regions surrounding the central vertex.	The edge-first projection of the 5-cell into 3 dimensions has a triangular dipyramidal envelope. The closest edge (shown here in red) projects to the axis of the dipyramid, with the three cells surrounding it projecting to 3 tetrahedral volumes arranged around this axis at 120 degrees to each other. The remaining 2 cells project to the two halves of the dipyramid and are on the far side of the pentatope.
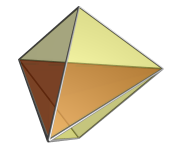The face-first projection of the 5-cell into 3 dimensions also has a triangular dipyramidal envelope. The nearest face is shown here in red. The two cells that meet at this face project to the two halves of the dipyramid. The remaining three cells are on the far side of the pentatope from the 4D viewpoint, and are culled from the image for clarity. They are arranged around the central axis of the dipyramid, just as in the edge-first projection.	The cell-first projection of the 5-cell into 3 dimensions has a tetrahedral envelope. The nearest cell projects onto the entire envelope, and, from the 4D viewpoint, obscures the other 4 cells; hence, they are not rendered here.

Irregular 5-cell

There are many lower symmetry forms, including these found in uniform polytope vertex figures:

Symmetry	[3,3,3] Order 120	[3,3,1] Order 24	[3,2,1] Order 12	[3,1,1] Order 6	[5,2]⁺ Order 10
Name	Regular 5-cell	Tetrahedral pyramid	Triangular-pyramidal pyramid		Pentagonal hyperdisphenoid
Schläfli	{3,3,3}	{3,3} ∨ ( )	{3} ∨ { }
Example Vertex figure	5-simplex	Truncated 5-simplex	Bitruncated 5-simplex	Cantitruncated 5-simplex	Omnitruncated 4-simplex honeycomb

The tetrahedral pyramid is a special case of a 5-cell, a polyhedral pyramid, constructed as a regular tetrahedron base in a 3-space hyperplane, and an apex point above the hyperplane. The four sides of the pyramid are made of tetrahedron cells.

Many uniform 5-polytopes have tetrahedral pyramid vertex figures:

Symmetry [3,3,1], order 24
Name Coxeter	{ }×{3,3,3}	{ }×{4,3,3}	{ }×{5,3,3}	t{3,3,3,3}	t{4,3,3,3}	t{3,4,3,3}
Schlegel diagram

Other uniform 5-polytopes have irregular 5-cell vertex figures. The symmetry of a vertex figure of a uniform polytope is represented by removing the ringed nodes of the Coxeter diagram.

Symmetry	[3,2,1], order 12		[3,1,1], order 6		[2⁺,4,1], order 8	[2,1,1], order 4
Schlegel diagram
Name Coxeter	t₁₂α₅	t₁₂γ₅	t₀₁₂α₅	t₀₁₂γ₅	t₁₂₃α₅	t₁₂₃γ₅

Symmetry	[2,1,1], order 2			[2⁺,1,1], order 2	[ ]⁺, order 1
Schlegel diagram
Name Coxeter	t₀₁₂₃α₅	t₀₁₂₃γ₅	t₀₁₂₃β₅	t₀₁₂₃₄α₅	t₀₁₂₃₄γ₅

Compound

The compound of two 5-cells in dual configurations can be seen in this A5 Coxeter plane projection, with a red and blue 5-cell vertices and edges. This compound has [[3,3,3]] symmetry, order 240. The intersection of these two 5-cells is a uniform bitruncated 5-cell. = ∩ .

This compound can be seen as the 4D analogue of the 2D hexagram {6⁄2} and the 3D compound of two tetrahedra.

Related polytopes and honeycombs

The pentachoron (5-cell) is the simplest of 9 uniform polychora constructed from the [3,3,3] Coxeter group.

Schläfli	{3,3,3}	t{3,3,3}	r{3,3,3}	rr{3,3,3}	2t{3,3,3}	tr{3,3,3}	t_0,3{3,3,3}	t_0,1,3{3,3,3}	t_0,1,2,3{3,3,3}
Coxeter
Schlegel

1_k2 figures in n dimensions
Space	Finite						Euclidean	Hyperbolic
n	3	4	5	6	7	8	9	10
Coxeter group	E₃=A₂A₁	E₄=A₄	E₅=D₅	E₆	E₇	E₈	E₉ = ${\tilde {E}}_{8}$ = E₈⁺	E₁₀ = ${\bar {T}}_{8}$ = E₈⁺⁺
Coxeter diagram
Symmetry (order)	[3^−1,2,1]	[3^0,2,1]	[3^1,2,1]	[[3^2,2,1]]	[3^3,2,1]	[3^4,2,1]	[3^5,2,1]	[3^6,2,1]
Order	12	120	1,920	103,680	2,903,040	696,729,600	∞
Graph							-	-
Name	1_−1,2	1₀₂	1₁₂	1₂₂	1₃₂	1₄₂	1₅₂	1₆₂

2_k1 figures in n dimensions
Space	Finite						Euclidean	Hyperbolic
n	3	4	5	6	7	8	9	10
Coxeter group	E₃=A₂A₁	E₄=A₄	E₅=D₅	E₆	E₇	E₈	E₉ = ${\tilde {E}}_{8}$ = E₈⁺	E₁₀ = ${\bar {T}}_{8}$ = E₈⁺⁺
Coxeter diagram
Symmetry	[3^−1,2,1]	[3^0,2,1]	[[3^1,2,1]]	[3^2,2,1]	[3^3,2,1]	[3^4,2,1]	[3^5,2,1]	[3^6,2,1]
Order	12	120	384	51,840	2,903,040	696,729,600	∞
Graph							-	-
Name	2_−1,1	2₀₁	2₁₁	2₂₁	2₃₁	2₄₁	2₅₁	2₆₁

It is in the sequence of regular polychora: the tesseract {4,3,3}, 120-cell {5,3,3}, of Euclidean 4-space, and hexagonal tiling honeycomb {6,3,3} of hyperbolic space. All of these have a tetrahedral vertex figure.

{p,3,3} polytopes
Space	S³			H³
Form	Finite			Paracompact	Noncompact
Name	{3,3,3}	{4,3,3}	{5,3,3}	{6,3,3}	{7,3,3}	{8,3,3}	...{∞,3,3}
Image
Cells {p,3}	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}

It is one of three regular 4-polytopes with tetrahedral cells, along with the 16-cell {3,3,5}, 600-cell {3,3,5}. The order-6 tetrahedral honeycomb {3,3,6} of hyperbolic space also has tetrahedral cells.

{3,3,p} polytopes
Space	S³			H³
Form	Finite			Paracompact	Noncompact
Name	{3,3,3}	{3,3,4}	{3,3,5}	{3,3,6}	{3,3,7}	{3,3,8}	... {3,3,∞}
Image
Vertex figure	{3,3}	{3,4}	{3,5}	{3,6}	{3,7}	{3,8}	{3,∞}

{3,p,3} polytopes
Space	S³		H³
Form	Finite		Compact	Paracompact	Noncompact
{3,p,3}	{3,3,3}	{3,4,3}	{3,5,3}	{3,6,3}	{3,7,3}	{3,8,3}	... {3,∞,3}
Image
Cells	{3,3}	{3,4}	{3,5}	{3,6}	{3,7}	{3,8}	{3,∞}
Vertex figure	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}

{p,3,p} regular honeycombs
Space	S³	Euclidean E³	H³
Form	Finite	Affine	Compact	Paracompact	Noncompact
Name	{3,3,3}	{4,3,4}	{5,3,5}	{6,3,6}	{7,3,7}	{8,3,8}	...{∞,3,∞}
Image
Cells	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}
Vertex figure	{3,3}	{3,4}	{3,5}	{3,6}	{3,7}	{3,8}	{3,∞}

Citations

^ N.W. Johnson: Geometries and Transformations, (2018) ISBN 978-1-107-10340-5 Chapter 11: Finite Symmetry Groups, 11.5 Spherical Coxeter groups, p.249
^ Matila Ghyka, The geometry of Art and Life (1977), p.68
^ Coxeter 1973, p. 120, §7.2. see illustration Fig 7.2A.
^ Category 1: Regular Polychora
^ Coxeter 1973, p. 12, §1.8. Configurations.
^ Coxeter 1991, p. 30, §4.2. The Crystallographic regular polytopes.

References

T. Gosset: On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900
H.S.M. Coxeter:
- Coxeter, H.S.M. (1973). Regular Polytopes (3rd ed.). New York: Dover.
  - p. 120, §7.2. see illustration Fig 7.2A
  - p. 296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
- Coxeter, H.S.M. (1991), Regular Complex Polytopes (2nd ed.), Cambridge: Cambridge University Press
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
  - (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
  - (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
  - (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26. pp. 409: Hemicubes: 1_n1)
Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. (1966)

External links

Weisstein, Eric W. "Pentatope". MathWorld.
Olshevsky, George. "Pentachoron". Glossary for Hyperspace. Archived from the original on 4 February 2007.
- 1. Convex uniform polychora based on the pentachoron - Model 1, George Olshevsky.
Klitzing, Richard. "4D uniform polytopes (polychora) x3o3o3o - pen".
Der 5-Zeller (5-cell) Marco Möller's Regular polytopes in R⁴ (German)
Jonathan Bowers, Regular polychora
Java3D Applets
pyrochoron

v t e Fundamental convex regular and uniform polytopes in dimensions 2–10
Family	A_n	B_n	I₂(p) / D_n	E₆ / E₇ / E₈ / F₄ / G₂	H_n
Regular polygon	Triangle	Square	p-gon	Hexagon	Pentagon
Uniform polyhedron	Tetrahedron	Octahedron • Cube	Demicube		Dodecahedron • Icosahedron
Uniform polychoron	Pentachoron	16-cell • Tesseract	Demitesseract	24-cell	120-cell • 600-cell
Uniform 5-polytope	5-simplex	5-orthoplex • 5-cube	5-demicube
Uniform 6-polytope	6-simplex	6-orthoplex • 6-cube	6-demicube	1₂₂ • 2₂₁
Uniform 7-polytope	7-simplex	7-orthoplex • 7-cube	7-demicube	1₃₂ • 2₃₁ • 3₂₁
Uniform 8-polytope	8-simplex	8-orthoplex • 8-cube	8-demicube	1₄₂ • 2₄₁ • 4₂₁
Uniform 9-polytope	9-simplex	9-orthoplex • 9-cube	9-demicube
Uniform 10-polytope	10-simplex	10-orthoplex • 10-cube	10-demicube
Uniform n-polytope	n-simplex	n-orthoplex • n-cube	n-demicube	1_k2 • 2_k1 • k₂₁	n-pentagonal polytope
Topics: Polytope families • Regular polytope • List of regular polytopes and compounds

[1] N.W. Johnson: Geometries and Transformations, (2018) ISBN 978-1-107-10340-5 Chapter 11: Finite Symmetry Groups, 11.5 Spherical Coxeter groups, p.249

[2] Matila Ghyka, The geometry of Art and Life (1977), p.68

[FOOTNOTECoxeter1973120§7.2._see_illustration_Fig_7.2<small>A</small>-3] Coxeter 1973, p. 120, §7.2. see illustration Fig 7.2A.

[4] Category 1: Regular Polychora

[FOOTNOTECoxeter197312§1.8._Configurations-5] Coxeter 1973, p. 12, §1.8. Configurations.

[FOOTNOTECoxeter199130§4.2._The_Crystallographic_regular_polytopes-6] Coxeter 1991, p. 30, §4.2. The Crystallographic regular polytopes.

[1]

[2]

[3]

[4]

[5]

[6]