5-simplex

5-simplex Hexateron (hix)
Type	uniform 5-polytope
Schläfli symbol	{34}
Coxeter diagram
4-faces	6	6 {3,3,3}
Cells	15	15 {3,3}
Faces	20	20 {3}
Edges	15
Vertices	6
Vertex figure	5-cell
Coxeter group	A5, [34], order 720
Dual	self-dual
Base point	(0,0,0,0,0,1)
Circumradius	0.645497
Properties	convex, isogonal regular, self-dual

In five-dimensional geometry, a 5-simplex is a self-dual regular 5-polytope. It has six vertices, 15 edges, 20 triangle faces, 15 tetrahedral cells, and 6 5-cell facets. It has a dihedral angle of cos⁻¹(⁠1/5⁠), or approximately 78.46°.

The 5-simplex is a solution to the problem: Make 20 equilateral triangles using 15 matchsticks, where each side of every triangle is exactly one matchstick.

Alternate names

It can also be called a hexateron, or hexa-5-tope, as a 6-facetted polytope in 5-dimensions. The name hexateron is derived from hexa- for having six facets and teron (with ter- being a corruption of tetra-) for having four-dimensional facets.

By Jonathan Bowers, a hexateron is given the acronym hix.

As a configuration

The elements of the regular polytopes can be expressed in a configuration matrix. Rows and columns reference vertices, edges, faces, and cells, with diagonal element their counts (f-vectors). The nondiagonal elements represent the number of row elements are incident to the column element. The configurations for dual polytopes can be seen by rotating the matrix elements by 180 degrees.

${\begin{bmatrix}{\begin{matrix}6&5&10&10&5\\2&15&4&6&4\\3&3&20&3&3\\4&6&4&15&2\\5&10&10&5&6\end{matrix}}\end{bmatrix}}$

Regular hexateron cartesian coordinates

The hexateron can be constructed from a 5-cell by adding a 6th vertex such that it is equidistant from all the other vertices of the 5-cell.

The Cartesian coordinates for the vertices of an origin-centered regular hexateron having edge length 2 are:

${\begin{aligned}&\left({\tfrac {1}{\sqrt {15}}},\ {\tfrac {1}{\sqrt {10}}},\ {\tfrac {1}{\sqrt {6}}},\ {\tfrac {1}{\sqrt {3}}},\ \pm 1\right)\\[5pt]&\left({\tfrac {1}{\sqrt {15}}},\ {\tfrac {1}{\sqrt {10}}},\ {\tfrac {1}{\sqrt {6}}},\ -{\tfrac {2}{\sqrt {3}}},\ 0\right)\\[5pt]&\left({\tfrac {1}{\sqrt {15}}},\ {\tfrac {1}{\sqrt {10}}},\ -{\tfrac {\sqrt {3}}{\sqrt {2}}},\ 0,\ 0\right)\\[5pt]&\left({\tfrac {1}{\sqrt {15}}},\ -{\tfrac {2{\sqrt {2}}}{\sqrt {5}}},\ 0,\ 0,\ 0\right)\\[5pt]&\left(-{\tfrac {\sqrt {5}}{\sqrt {3}}},\ 0,\ 0,\ 0,\ 0\right)\end{aligned}}$

The vertices of the 5-simplex can be more simply positioned on a hyperplane in 6-space as permutations of (0,0,0,0,0,1) or (0,1,1,1,1,1). These construction can be seen as facets of the 6-orthoplex or rectified 6-cube respectively.

Projected images

orthographic projections

Ak Coxeter plane	A5	A4
Graph
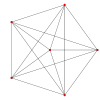
Dihedral symmetry	[6]	[5]
Ak Coxeter plane	A3	A2
Graph
Dihedral symmetry	[4]	[3]

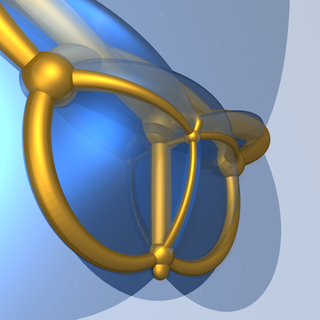Stereographic projection 4D to 3D of Schlegel diagram 5D to 4D of hexateron.

Lower symmetry forms

A lower symmetry form is a 5-cell pyramid ( )v{3,3,3}, with [3,3,3] symmetry order 120, constructed as a 5-cell base in a 4-space hyperplane, and an apex point above the hyperplane. The five sides of the pyramid are made of 5-cell cells. These are seen as vertex figures of truncated regular 6-polytopes, like a truncated 6-cube.

Another form is { }v{3,3}, with [2,3,3] symmetry order 48, the joining of an orthogonal digon and a tetrahedron, orthogonally offset, with all pairs of vertices connected between. Another form is {3}v{3}, with [3,2,3] symmetry order 36, and extended symmetry [[3,2,3]], order 72. It represents joining of 2 orthogonal triangles, orthogonally offset, with all pairs of vertices connected between.

These are seen in the vertex figures of bitruncated and tritruncated regular 6-polytopes, like a bitruncated 6-cube and a tritruncated 6-simplex. The edge labels here represent the types of face along that direction, and thus represent different edge lengths.

Vertex figures for truncated 6-simplexes

( )v{3,3,3}		{ }v{3,3}		{3}v{3}
truncated 6-simplex	truncated 6-cube	bitruncated 6-simplex	bitruncated 6-cube	tritruncated 6-simplex

Compound

The compound of two 5-simplexes in dual configurations can be seen in this A6 Coxeter plane projection, with a red and blue 5-simplex vertices and edges. This compound has [[3,3,3,3]] symmetry, order 1440. The intersection of these two 5-simplexes is a uniform birectified 5-simplex. = ∩ .

Related uniform 5-polytopes

It is first in a dimensional series of uniform polytopes and honeycombs, expressed by Coxeter as 1_3k series. A degenerate 4-dimensional case exists as 3-sphere tiling, a tetrahedral dihedron.

1_3k dimensional figures

Space	Finite				Euclidean	Hyperbolic
n	4	5	6	7	8	9
Coxeter group	A3A1	A5	D6	E7	${\tilde {E}}_{7}$=E7+	${\bar {T}}_{8}$=E7++
Coxeter diagram
Symmetry	[3−1,3,1]	[30,3,1]	[31,3,1]	[32,3,1]	[[33,3,1]]	[34,3,1]
Order	48	720	23,040	2,903,040	∞
Graph					-	-
Name	13,-1	130	131	132	133	134

It is first in a dimensional series of uniform polytopes and honeycombs, expressed by Coxeter as 3_k1 series. A degenerate 4-dimensional case exists as 3-sphere tiling, a tetrahedral hosohedron.

3_k1 dimensional figures

Space	Finite				Euclidean	Hyperbolic
n	4	5	6	7	8	9
Coxeter group	A3A1	A5	D6	E7	${\tilde {E}}_{7}$=E7+	${\bar {T}}_{8}$=E7++
Coxeter diagram
Symmetry	[3−1,3,1]	[30,3,1]	[[31,3,1]] = [4,3,3,3,3]	[32,3,1]	[33,3,1]	[34,3,1]
Order	48	720	46,080	2,903,040	∞
Graph					-	-
Name	31,-1	310	311	321	331	341

The 5-simplex, as 2₂₀ polytope is first in dimensional series 2_2k.

2_2k figures of n dimensions

Space	Finite			Euclidean	Hyperbolic
n	4	5	6	7	8
Coxeter group	A2A2	A5	E6	${\tilde {E}}_{6}$=E6+	E6++
Coxeter diagram
Graph				∞	∞
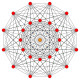
Name	22,-1	220	221	222	223

The regular 5-simplex is one of 19 uniform polytera based on the [3,3,3,3] Coxeter group, all shown here in A₅ Coxeter plane orthographic projections. (Vertices are colored by projection overlap order, red, orange, yellow, green, cyan, blue, purple having progressively more vertices)

References

• T. Gosset: On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900
• H.S.M. Coxeter:
  • Coxeter, Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8, p.296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
  • H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973, p.296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
  • Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
    • (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
    • (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
    • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
• John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26. pp. 409: Hemicubes: 1_n1)
• Norman Johnson Uniform Polytopes, Manuscript (1991)
  • N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. (1966)
• Klitzing, Richard. "5D uniform polytopes (polytera) x3o3o3o3o - hix".

External links

• Olshevsky, George. "Simplex". Glossary for Hyperspace. Archived from the original on 4 February 2007.
• Polytopes of Various Dimensions, Jonathan Bowers
• Multi-dimensional Glossary