Gauss's law

In physics (specifically electromagnetism), Gauss's law, also known as Gauss's flux theorem, (or sometimes simply called Gauss's theorem) is one of Maxwell's equations. It relates the distribution of electric charge to the resulting electric field.
Definition[edit]
In its integral form, it states that the flux of the electric field out of an arbitrary closed surface is proportional to the electric charge enclosed by the surface, irrespective of how that charge is distributed. Even though the law alone is insufficient to determine the electric field across a surface enclosing any charge distribution, this may be possible in cases where symmetry mandates uniformity of the field. Where no such symmetry exists, Gauss's law can be used in its differential form, which states that the divergence of the electric field is proportional to the local density of charge.
The law was first[1] formulated by Joseph-Louis Lagrange in 1773,[2] followed by Carl Friedrich Gauss in 1835,[3] both in the context of the attraction of ellipsoids. It is one of Maxwell's equations, which forms the basis of classical electrodynamics.[note 1] Gauss's law can be used to derive Coulomb's law,[4] and vice versa.
| Articles about |
| Electromagnetism |
|---|
 |
Qualitative description[edit]
In words, Gauss's law states:
- The net electric flux through any hypothetical closed surface is equal to 1/ε0 times the net electric charge enclosed within that closed surface. The closed surface is also referred to as Gaussian surface.[5]
Gauss's law has a close mathematical similarity with a number of laws in other areas of physics, such as Gauss's law for magnetism and Gauss's law for gravity. In fact, any inverse-square law can be formulated in a way similar to Gauss's law: for example, Gauss's law itself is essentially equivalent to the Coulomb's law, and Gauss's law for gravity is essentially equivalent to the Newton's law of gravity, both of which are inverse-square laws.
The law can be expressed mathematically using vector calculus in integral form and differential form; both are equivalent since they are related by the divergence theorem, also called Gauss's theorem. Each of these forms in turn can also be expressed two ways: In terms of a relation between the electric field E and the total electric charge, or in terms of the electric displacement field D and the free electric charge.[6]
Equation involving the E field[edit]
Gauss's law can be stated using either the electric field E or the electric displacement field D. This section shows some of the forms with E; the form with D is below, as are other forms with E.
Integral form[edit]


Gauss's law may be expressed as:[6]
where ΦE is the electric flux through a closed surface S enclosing any volume V, Q is the total charge enclosed within V, and ε0 is the electric constant. The electric flux ΦE is defined as a surface integral of the electric field:
where E is the electric field, dA is a vector representing an infinitesimal element of area of the surface,[note 2] and · represents the dot product of two vectors.
In a curved spacetime, the flux of an electromagnetic field through a closed surface is expressed as
where is the speed of light; denotes the time components of the electromagnetic tensor; is the determinant of metric tensor; is an orthonormal element of the two-dimensional surface surrounding the charge ; indices and do not match each other.[8]
Since the flux is defined as an integral of the electric field, this expression of Gauss's law is called the integral form.
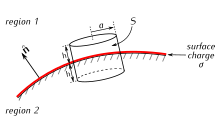
In problems involving conductors set at known potentials, the potential away from them is obtained by solving Laplace's equation, either analytically or numerically. The electric field is then calculated as the potential's negative gradient. Gauss's law makes it possible to find the distribution of electric charge: The charge in any given region of the conductor can be deduced by integrating the electric field to find the flux through a small box whose sides are perpendicular to the conductor's surface and by noting that the electric field is perpendicular to the surface, and zero inside the conductor.
The reverse problem, when the electric charge distribution is known and the electric field must be computed, is much more difficult. The total flux through a given surface gives little information about the electric field, and can go in and out of the surface in arbitrarily complicated patterns.
An exception is if there is some symmetry in the problem, which mandates that the electric field passes through the surface in a uniform way. Then, if the total flux is known, the field itself can be deduced at every point. Common examples of symmetries which lend themselves to Gauss's law include: cylindrical symmetry, planar symmetry, and spherical symmetry. See the article Gaussian surface for examples where these symmetries are exploited to compute electric fields.
Differential form[edit]
By the divergence theorem, Gauss's law can alternatively be written in the differential form:
where ∇ · E is the divergence of the electric field, ε0 is the vacuum permittivity, is the relative permittivity, and ρ is the volume charge density (charge per unit volume).
Equivalence of integral and differential forms[edit]
The integral and differential forms are mathematically equivalent, by the divergence theorem. Here is the argument more specifically.
The integral form of Gauss' law is:
for any closed surface S containing charge Q. By the divergence theorem, this equation is equivalent to:
for any volume V containing charge Q. By the relation between charge and charge density, this equation is equivalent to:
Equation involving the D field[edit]
Free, bound, and total charge[edit]
The electric charge that arises in the simplest textbook situations would be classified as "free charge"—for example, the charge which is transferred in static electricity, or the charge on a capacitor plate. In contrast, "bound charge" arises only in the context of dielectric (polarizable) materials. (All materials are polarizable to some extent.) When such materials are placed in an external electric field, the electrons remain bound to their respective atoms, but shift a microscopic distance in response to the field, so that they're more on one side of the atom than the other. All these microscopic displacements add up to give a macroscopic net charge distribution, and this constitutes the "bound charge".
Although microscopically all charge is fundamentally the same, there are often practical reasons for wanting to treat bound charge differently from free charge. The result is that the more fundamental Gauss's law, in terms of E (above), is sometimes put into the equivalent form below, which is in terms of D and the free charge only.
Integral form[edit]
This formulation of Gauss's law states the total charge form:
where ΦD is the D-field flux through a surface S which encloses a volume V, and Qfree is the free charge contained in V. The flux ΦD is defined analogously to the flux ΦE of the electric field E through S:
Differential form[edit]
The differential form of Gauss's law, involving free charge only, states:
where ∇ · D is the divergence of the electric displacement field, and ρfree is the free electric charge density.
Equivalence of total and free charge statements[edit]
In this proof, we will show that the equation
We introduce the polarization density P, which has the following relation to E and D:
Equation for linear materials[edit]
In homogeneous, isotropic, nondispersive, linear materials, there is a simple relationship between E and D:
where ε is the permittivity of the material. For the case of vacuum (aka free space), ε = ε0. Under these circumstances, Gauss's law modifies to
for the integral form, and
for the differential form.
Relation to Coulomb's law[edit]
This article duplicates the scope of other articles, specifically Coulomb's_law#Relation_to_Gauss's_law. |
Deriving Gauss's law from Coulomb's law[edit]
Strictly speaking, Gauss's law cannot be derived from Coulomb's law alone, since Coulomb's law gives the electric field due to an individual, electrostatic point charge only. However, Gauss's law can be proven from Coulomb's law if it is assumed, in addition, that the electric field obeys the superposition principle. The superposition principle states that the resulting field is the vector sum of fields generated by each particle (or the integral, if the charges are distributed smoothly in space).
Coulomb's law states that the electric field due to a stationary point charge is:
- er is the radial unit vector,
- r is the radius, |r|,
- ε0 is the electric constant,
- q is the charge of the particle, which is assumed to be located at the origin.
Using the expression from Coulomb's law, we get the total field at r by using an integral to sum the field at r due to the infinitesimal charge at each other point s in space, to give
Using the "shifting property" of the Dirac delta function, we arrive at
Since Coulomb's law only applies to stationary charges, there is no reason to expect Gauss's law to hold for moving charges based on this derivation alone. In fact, Gauss's law does hold for moving charges, and, in this respect, Gauss's law is more general than Coulomb's law.
Let be a bounded open set, and
It is true for all that .
Consider now a compact set having a piecewise smooth boundary such that . It follows that and so, for the divergence theorem:
But because ,
Therefore the flux through a closed surface generated by some charge density outside (the surface) is null.
Now consider , and as the sphere centered in having as radius (it exists because is an open set).
Let and be the electric field created inside and outside the sphere respectively. Then,
- , and
The last equality follows by observing that , and the argument above.
The RHS is the electric flux generated by a charged sphere, and so:
Where the last equality follows by the mean value theorem for integrals. Using the squeeze theorem and the continuity of , one arrives at:
Deriving Coulomb's law from Gauss's law[edit]
Strictly speaking, Coulomb's law cannot be derived from Gauss's law alone, since Gauss's law does not give any information regarding the curl of E (see Helmholtz decomposition and Faraday's law). However, Coulomb's law can be proven from Gauss's law if it is assumed, in addition, that the electric field from a point charge is spherically symmetric (this assumption, like Coulomb's law itself, is exactly true if the charge is stationary, and approximately true if the charge is in motion).
Taking S in the integral form of Gauss' law to be a spherical surface of radius r, centered at the point charge Q, we have
By the assumption of spherical symmetry, the integrand is a constant which can be taken out of the integral. The result is
See also[edit]
Notes[edit]
- ^ The other three of Maxwell's equations are: Gauss's law for magnetism, Faraday's law of induction, and Ampère's law with Maxwell's correction
- ^ More specifically, the infinitesimal area is thought of as planar and with area dN. The vector dR is normal to this area element and has magnitude dA.[7]
Citations[edit]
- ^ Duhem, Pierre (1891). "4". Leçons sur l'électricité et le magnétisme [Lessons on electricity and magnetism] (in French). Vol. 1. Paris Gauthier-Villars. pp. 22–23. OCLC 1048238688. OL 23310906M. Shows that Lagrange has priority over Gauss. Others after Gauss discovered "Gauss's Law", too.
- ^ Lagrange, Joseph-Louis (1869) [1776]. Serret, Joseph-Alfred; Darboux, Jean-Gaston (eds.). "Sur l'attraction des sphéroïdes elliptiques" [On the attraction of elliptical spheroids]. Œuvres de Lagrange: Mémoires extraits des recueils de l'Académie royale des sciences et belles-lettres de Berlin (in French). Gauthier-Villars: 619.
- ^ Gauss, Carl Friedrich (1877). "Theoria attractionis corporum sphaeroidicorum ellipticorum homogeneorum methodo nova tractata" [The theory of the attraction of homogeneous spheroidal elliptic bodies treated by a new method]. In Schering, Ernst Christian Julius; Brendel, Martin (eds.). Carl Friedrich Gauss Werke [Works of Carl Friedrich Gauss] (in Latin and German). Vol. 5 (2nd ed.). Gedruckt in der Dieterichschen Universitätsdruckerei (W.F. Kaestner). pp. 2–22. Gauss mentions Newton's Principia proposition XCI regarding finding the force exerted by a sphere on a point anywhere along an axis passing through the sphere.
- ^ Halliday, David; Resnick, Robert (1970). Fundamentals of Physics. John Wiley & Sons. pp. 452–453.
- ^ Serway, Raymond A. (1996). Physics for Scientists and Engineers with Modern Physics (4th ed.). p. 687.
- ^ a b Grant, I. S.; Phillips, W. R. (2008). Electromagnetism. Manchester Physics (2nd ed.). John Wiley & Sons. ISBN 978-0-471-92712-9.
- ^ Matthews, Paul (1998). Vector Calculus. Springer. ISBN 3-540-76180-2.
- ^ Fedosin, Sergey G. (2019). "On the Covariant Representation of Integral Equations of the Electromagnetic Field". Progress in Electromagnetics Research C. 96: 109–122. arXiv:1911.11138. Bibcode:2019arXiv191111138F. doi:10.2528/PIERC19062902. S2CID 208095922.
- ^ See, for example, Griffiths, David J. (2013). Introduction to Electrodynamics (4th ed.). Prentice Hall. p. 50.
References[edit]
- Gauss, Carl Friedrich (1867). Werke Band 5. Digital version
- Jackson, John David (1998). Classical Electrodynamics (3rd ed.). New York: Wiley. ISBN 0-471-30932-X. David J. Griffiths (6th ed.)
External links[edit]
 Media related to Gauss' Law at Wikimedia Commons
Media related to Gauss' Law at Wikimedia Commons- MIT Video Lecture Series (30 x 50 minute lectures)- Electricity and Magnetism Taught by Professor Walter Lewin.
- section on Gauss's law in an online textbook Archived 2010-05-27 at the Wayback Machine
- MISN-0-132 Gauss's Law for Spherical Symmetry (PDF file) by Peter Signell for Project PHYSNET.
- MISN-0-133 Gauss's Law Applied to Cylindrical and Planar Charge Distributions (PDF file) by Peter Signell for Project PHYSNET.


































































