Bifurcation theory
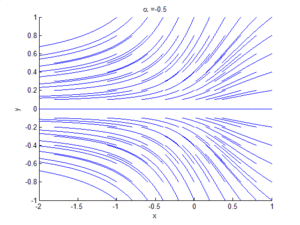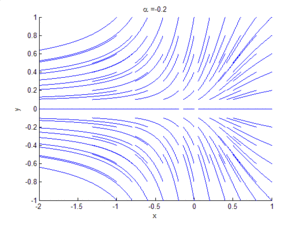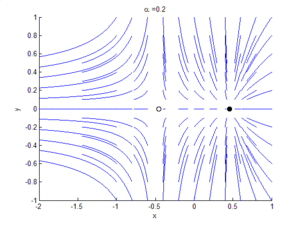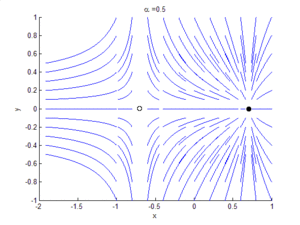
Bifurcation theory is the mathematical study of changes in the qualitative or topological structure of a given family of curves, such as the integral curves of a family of vector fields, and the solutions of a family of differential equations. Most commonly applied to the mathematical study of dynamical systems, a bifurcation occurs when a small smooth change made to the parameter values (the bifurcation parameters) of a system causes a sudden 'qualitative' or topological change in its behavior.[1] Bifurcations occur in both continuous systems (described by ordinary, delay or partial differential equations) and discrete systems (described by maps).
The name "bifurcation" was first introduced by Henri Poincaré in 1885 in the first paper in mathematics showing such a behavior.[2]
Bifurcation types[edit]
It is useful to divide bifurcations into two principal classes:
- Local bifurcations, which can be analysed entirely through changes in the local stability properties of equilibria, periodic orbits or other invariant sets as parameters cross through critical thresholds; and
- Global bifurcations, which often occur when larger invariant sets of the system 'collide' with each other, or with equilibria of the system. They cannot be detected purely by a stability analysis of the equilibria (fixed points).
Local bifurcations[edit]

A local bifurcation occurs when a parameter change causes the stability of an equilibrium (or fixed point) to change. In continuous systems, this corresponds to the real part of an eigenvalue of an equilibrium passing through zero. In discrete systems (described by maps), this corresponds to a fixed point having a Floquet multiplier with modulus equal to one. In both cases, the equilibrium is non-hyperbolic at the bifurcation point. The topological changes in the phase portrait of the system can be confined to arbitrarily small neighbourhoods of the bifurcating fixed points by moving the bifurcation parameter close to the bifurcation point (hence 'local').
More technically, consider the continuous dynamical system described by the ordinary differential equation (ODE)
For discrete dynamical systems, consider the system
Examples of local bifurcations include:
- Saddle-node (fold) bifurcation
- Transcritical bifurcation
- Pitchfork bifurcation
- Period-doubling (flip) bifurcation
- Hopf bifurcation
- Neimark–Sacker (secondary Hopf) bifurcation
Global bifurcations[edit]

Global bifurcations occur when 'larger' invariant sets, such as periodic orbits, collide with equilibria. This causes changes in the topology of the trajectories in the phase space which cannot be confined to a small neighbourhood, as is the case with local bifurcations. In fact, the changes in topology extend out to an arbitrarily large distance (hence 'global').
Examples of global bifurcations include:
- Homoclinic bifurcation in which a limit cycle collides with a saddle point.[3] Homoclinic bifurcations can occur supercritically or subcritically. The variant above is the "small" or "type I" homoclinic bifurcation. In 2D there is also the "big" or "type II" homoclinic bifurcation in which the homoclinic orbit "traps" the other ends of the unstable and stable manifolds of the saddle. In three or more dimensions, higher codimension bifurcations can occur, producing complicated, possibly chaotic dynamics.
- Heteroclinic bifurcation in which a limit cycle collides with two or more saddle points; they involve a heteroclinic cycle.[4] Heteroclinic bifurcations are of two types: resonance bifurcations and transverse bifurcations. Both types of bifurcation will result in the change of stability of the heteroclinic cycle. At a resonance bifurcation, the stability of the cycle changes when an algebraic condition on the eigenvalues of the equilibria in the cycle is satisfied. This is usually accompanied by the birth or death of a periodic orbit. A transverse bifurcation of a heteroclinic cycle is caused when the real part of a transverse eigenvalue of one of the equilibria in the cycle passes through zero. This will also cause a change in stability of the heteroclinic cycle.
- Infinite-period bifurcation in which a stable node and saddle point simultaneously occur on a limit cycle.[5] As the limit of a parameter approaches a certain critical value, the speed of the oscillation slows down and the period approaches infinity. The infinite-period bifurcation occurs at this critical value. Beyond the critical value, the two fixed points emerge continuously from each other on the limit cycle to disrupt the oscillation and form two saddle points.
- Blue sky catastrophe in which a limit cycle collides with a nonhyperbolic cycle.
Global bifurcations can also involve more complicated sets such as chaotic attractors (e.g. crises).
- Examples of bifurcations
-
A Hopf bifurcation occurs in the system and , when , around the origin. A homoclinic bifurcation occurs around .
-
A detailed view of the homoclinic bifurcation.
-
As increases from zero, a stable limit cycle emerges out of the origin via Hopf bifurcation. Here we plot the limit cycle parametrically, up to order . The exact computation is explained on the Hopf bifurcation page.
Codimension of a bifurcation[edit]
The codimension of a bifurcation is the number of parameters which must be varied for the bifurcation to occur. This corresponds to the codimension of the parameter set for which the bifurcation occurs within the full space of parameters. Saddle-node bifurcations and Hopf bifurcations are the only generic local bifurcations which are really codimension-one (the others all having higher codimension). However, transcritical and pitchfork bifurcations are also often thought of as codimension-one, because the normal forms can be written with only one parameter.
An example of a well-studied codimension-two bifurcation is the Bogdanov–Takens bifurcation.
Applications in semiclassical and quantum physics[edit]
Bifurcation theory has been applied to connect quantum systems to the dynamics of their classical analogues in atomic systems,[6][7][8] molecular systems,[9] and resonant tunneling diodes.[10] Bifurcation theory has also been applied to the study of laser dynamics[11] and a number of theoretical examples which are difficult to access experimentally such as the kicked top[12] and coupled quantum wells.[13] The dominant reason for the link between quantum systems and bifurcations in the classical equations of motion is that at bifurcations, the signature of classical orbits becomes large, as Martin Gutzwiller points out in his classic[14] work on quantum chaos.[15] Many kinds of bifurcations have been studied with regard to links between classical and quantum dynamics including saddle node bifurcations, Hopf bifurcations, umbilic bifurcations, period doubling bifurcations, reconnection bifurcations, tangent bifurcations, and cusp bifurcations.
See also[edit]
- Bifurcation diagram
- Bifurcation memory
- Catastrophe theory
- Feigenbaum constants
- Geomagnetic reversal
- Phase portrait
- Tennis racket theorem
Notes[edit]
- ^ Blanchard, P.; Devaney, R. L.; Hall, G. R. (2006). Differential Equations. London: Thompson. pp. 96–111. ISBN 978-0-495-01265-8.
- ^ Henri Poincaré. "L'Équilibre d'une masse fluide animée d'un mouvement de rotation". Acta Mathematica, vol.7, pp. 259-380, Sept 1885.
- ^ Strogatz, Steven H. (1994). Nonlinear Dynamics and Chaos. Addison-Wesley. p. 262. ISBN 0-201-54344-3.
- ^ Luo, Dingjun (1997). Bifurcation Theory and Methods of Dynamical Systems. World Scientific. p. 26. ISBN 981-02-2094-4.
- ^ James P. Keener, "Infinite Period Bifurcation and Global Bifurcation Branches", SIAM Journal on Applied Mathematics, Vol. 41, No. 1 (August, 1981), pp. 127–144.
- ^ Gao, J.; Delos, J. B. (1997). "Quantum manifestations of bifurcations of closed orbits in the photoabsorption spectra of atoms in electric fields". Phys. Rev. A. 56 (1): 356–364. Bibcode:1997PhRvA..56..356G. doi:10.1103/PhysRevA.56.356. S2CID 120255640.
- ^ Peters, A. D.; Jaffé, C.; Delos, J. B. (1994). "Quantum Manifestations of Bifurcations of Classical Orbits: An Exactly Solvable Model". Phys. Rev. Lett. 73 (21): 2825–2828. Bibcode:1994PhRvL..73.2825P. doi:10.1103/PhysRevLett.73.2825. PMID 10057205. S2CID 1641622.
- ^ Courtney, Michael; Jiao, Hong; Spellmeyer, Neal; Kleppner, Daniel; Gao, J.; Delos, J. B.; et al. (1995). "Closed Orbit Bifurcations in Continuum Stark Spectra". Phys. Rev. Lett. 74 (9): 1538–1541. Bibcode:1995PhRvL..74.1538C. doi:10.1103/PhysRevLett.74.1538. PMID 10059054. S2CID 21573702.
- ^ Founargiotakis, M.; Farantos, S. C.; Skokos, Ch.; Contopoulos, G. (1997). "Bifurcation diagrams of periodic orbits for unbound molecular systems: FH2". Chemical Physics Letters. 277 (5–6): 456–464. Bibcode:1997CPL...277..456F. doi:10.1016/S0009-2614(97)00931-7.
- ^ Monteiro, T. S. & Saraga, D. S. (2001). "Quantum Wells in Tilted Fields:Semiclassical Amplitudes and Phase Coherence Times". Foundations of Physics. 31 (2): 355–370. Bibcode:2001FoPh...31..355M. doi:10.1023/A:1017546721313. S2CID 120968155.
- ^ Wieczorek, S.; Krauskopf, B.; Simpson, T. B. & Lenstra, D. (2005). "The dynamical complexity of optically injected semiconductor lasers". Physics Reports. 416 (1–2): 1–128. Bibcode:2005PhR...416....1W. doi:10.1016/j.physrep.2005.06.003.
- ^ Stamatiou, G. & Ghikas, D. P. K. (2007). "Quantum entanglement dependence on bifurcations and scars in non-autonomous systems. The case of quantum kicked top". Physics Letters A. 368 (3–4): 206–214. arXiv:quant-ph/0702172. Bibcode:2007PhLA..368..206S. doi:10.1016/j.physleta.2007.04.003. S2CID 15562617.
- ^ Galan, J.; Freire, E. (1999). "Chaos in a Mean Field Model of Coupled Quantum Wells; Bifurcations of Periodic Orbits in a Symmetric Hamiltonian System". Reports on Mathematical Physics. 44 (1–2): 87–94. Bibcode:1999RpMP...44...87G. doi:10.1016/S0034-4877(99)80148-7.
- ^ Kleppner, D.; Delos, J. B. (2001). "Beyond quantum mechanics: Insights from the work of Martin Gutzwiller". Foundations of Physics. 31 (4): 593–612. Bibcode:2001FoPh...31..593K. doi:10.1023/A:1017512925106. S2CID 116944147.
- ^ Gutzwiller, Martin C. (1990). Chaos in Classical and Quantum Mechanics. New York: Springer-Verlag. ISBN 978-0-387-97173-5.
References[edit]
- Afrajmovich, V. S.; Arnold, V. I.; et al. (1994). Bifurcation Theory and Catastrophe Theory. Springer. ISBN 978-3-540-65379-0.
- Guardia, M.; Martinez-Seara, M.; Teixeira, M. A. (2011). Generic bifurcations of low codimension of planar Filippov Systems. "Journal of differential equations", Febrer 2011, vol. 250, núm. 4, pp. 1967–2023. DOI:10.1016/j.jde.2010.11.016
- Wiggins, Stephen (1988). Global bifurcations and Chaos: Analytical Methods. New York: Springer. ISBN 978-0-387-96775-2.
External links[edit]
- Nonlinear dynamics
- Bifurcations and Two Dimensional Flows by Elmer G. Wiens
- Introduction to Bifurcation theory by John David Crawford















