Icositetragon
| Regular icositetragon | |
|---|---|
 A regular icositetragon | |
| Type | Regular polygon |
| Edges and vertices | 24 |
| Schläfli symbol | {24}, t{12}, tt{6}, ttt{3} |
| Coxeter–Dynkin diagrams | |
| Symmetry group | Dihedral (D24), order 2×24 |
| Internal angle (degrees) | 165° |
| Properties | Convex, cyclic, equilateral, isogonal, isotoxal |
| Dual polygon | Self |
In geometry, an icositetragon (or icosikaitetragon) or 24-gon is a twenty-four-sided polygon. The sum of any icositetragon's interior angles is 3960 degrees.
Regular icositetragon
[edit]The regular icositetragon is represented by Schläfli symbol {24} and can also be constructed as a truncated dodecagon, t{12}, or a twice-truncated hexagon, tt{6}, or thrice-truncated triangle, ttt{3}.
One interior angle in a regular icositetragon is 165°, meaning that one exterior angle would be 15°.
The area of a regular icositetragon is: (with t = edge length)
The icositetragon appeared in Archimedes' polygon approximation of pi, along with the hexagon (6-gon), dodecagon (12-gon), tetracontaoctagon (48-gon), and enneacontahexagon (96-gon).
Construction
[edit]As 24 = 23 × 3, a regular icositetragon is constructible using an angle trisector.[1] As a truncated dodecagon, it can be constructed by an edge-bisection of a regular dodecagon.
Symmetry
[edit]
The regular icositetragon has Dih24 symmetry, order 48. There are 7 subgroup dihedral symmetries: (Dih12, Dih6, Dih3), and (Dih8, Dih4, Dih2 Dih1), and 8 cyclic group symmetries: (Z24, Z12, Z6, Z3), and (Z8, Z4, Z2, Z1).
These 16 symmetries can be seen in 22 distinct symmetries on the icositetragon. John Conway labels these by a letter and group order.[2] The full symmetry of the regular form is r48 and no symmetry is labeled a1. The dihedral symmetries are divided depending on whether they pass through vertices (d for diagonal) or edges (p for perpendiculars), and i when reflection lines path through both edges and vertices. Cyclic symmetries in the middle column are labeled as g for their central gyration orders.
Each subgroup symmetry allows one or more degrees of freedom for irregular forms. Only the g24 subgroup has no degrees of freedom but can be seen as directed edges.
Dissection
[edit] regular |
 Isotoxal |
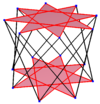
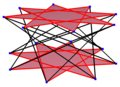
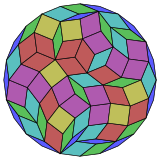
Coxeter states that every zonogon (a 2m-gon whose opposite sides are parallel and of equal length) can be dissected into m(m-1)/2 parallelograms.[3] In particular this is true for regular polygons with evenly many sides, in which case the parallelograms are all rhombi. For the regular icositetragon, m=12, and it can be divided into 66: 6 squares and 5 sets of 12 rhombs. This decomposition is based on a Petrie polygon projection of a 12-cube.
 12-cube |

|

|

|
|
Related polygons
[edit]
A regular triangle, octagon, and icositetragon can completely fill a plane vertex.
An icositetragram is a 24-sided star polygon. There are 3 regular forms given by Schläfli symbols: {24/5}, {24/7}, and {24/11}. There are also 7 regular star figures using the same vertex arrangement: 2{12}, 3{8}, 4{6}, 6{4}, 8{3}, 3{8/3}, and 2{12/5}.
| Icositetragrams as star polygons and star figures | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Form | Convex polygon | Compounds | Star polygon | Compound | |||||||
| Image |  {24/1}={24} |
 {24/2}=2{12} |
 {24/3}=3{8} |
 {24/4}=4{6} |
 {24/5} |
 {24/6}=6{4} | |||||
| Interior angle | 165° | 150° | 135° | 120° | 105° | 90° | |||||
| Form | Star polygon | Compounds | Star polygon | Compound | |||||||
| Image |  {24/7} |
 {24/8}=8{3} |
 {24/9}=3{8/3} |
 {24/10}=2{12/5} |
 {24/11} |
 {24/12}=12{2} | |||||
| Interior angle | 75° | 60° | 45° | 30° | 15° | 0° | |||||
There are also isogonal icositetragrams constructed as deeper truncations of the regular dodecagon {12} and dodecagram {12/5}. These also generate two quasitruncations: t{12/11}={24/11}, and t{12/7}={24/7}. [4]
| Isogonal truncations of regular dodecagon and dodecagram | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Quasiregular | Isogonal | Quasiregular | |||||||||
 t{12}={24} |

|

|

|

|

|
 t{12/11}={24/11} | |||||
 t{12/5}={24/5} |

|

|

|

|

|
 t{12/7}={24/7} | |||||
Skew icositetragon
[edit]A skew icositetragon is a skew polygon with 24 vertices and edges but not existing on the same plane. The interior of such an icositetragon is not generally defined. A skew zig-zag icositetragon has vertices alternating between two parallel planes.
A regular skew icositetragon is vertex-transitive with equal edge lengths. In 3-dimensions it will be a zig-zag skew icositetragon and can be seen in the vertices and side edges of a dodecagonal antiprism with the same D12d, [2+,24] symmetry, order 48. The dodecagrammic antiprism, s{2,24/5} and dodecagrammic crossed-antiprism, s{2,24/7} also have regular skew dodecagons.
Petrie polygons
[edit]The regular icositetragon is the Petrie polygon for many higher-dimensional polytopes, seen as orthogonal projections in Coxeter planes, including:
| 2F4 | ||
|---|---|---|
 Bitruncated 24-cell |
 Runcinated 24-cell |
 Omnitruncated 24-cell |
| E8 | ||
|---|---|---|
 421 |
 241 |
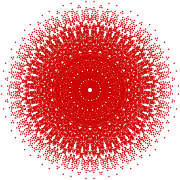 142 |
References
[edit]- ^ Constructible Polygon
- ^ John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things, ISBN 978-1-56881-220-5 (Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon pp. 275-278)
- ^ Coxeter, Mathematical recreations and Essays, Thirteenth edition, p.141
- ^ The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History, (1994), Metamorphoses of polygons, Branko Grünbaum