Topological space
In mathematics, a topological space is, roughly speaking, a geometrical space in which closeness is defined but cannot necessarily be measured by a numeric distance. More specifically, a topological space is a set whose elements are called points, along with an additional structure called a topology, which can be defined as a set of neighbourhoods for each point that satisfy some axioms formalizing the concept of closeness. There are several equivalent definitions of a topology, the most commonly used of which is the definition through open sets, which is easier than the others to manipulate.
A topological space is the most general type of a mathematical space that allows for the definition of limits, continuity, and connectedness.[1][2] Common types of topological spaces include Euclidean spaces, metric spaces and manifolds.
Although very general, the concept of topological spaces is fundamental, and used in virtually every branch of modern mathematics. The study of topological spaces in their own right is called point-set topology or general topology.
History[edit]
Around 1735, Leonhard Euler discovered the formula relating the number of vertices (V), edges (E) and faces (F) of a convex polyhedron, and hence of a planar graph. The study and generalization of this formula, specifically by Cauchy (1789–1857) and L'Huilier (1750–1840), boosted the study of topology. In 1827, Carl Friedrich Gauss published General investigations of curved surfaces, which in section 3 defines the curved surface in a similar manner to the modern topological understanding: "A curved surface is said to possess continuous curvature at one of its points A, if the direction of all the straight lines drawn from A to points of the surface at an infinitesimal distance from A are deflected infinitesimally from one and the same plane passing through A."[3]
Yet, "until Riemann's work in the early 1850s, surfaces were always dealt with from a local point of view (as parametric surfaces) and topological issues were never considered".[4] " Möbius and Jordan seem to be the first to realize that the main problem about the topology of (compact) surfaces is to find invariants (preferably numerical) to decide the equivalence of surfaces, that is, to decide whether two surfaces are homeomorphic or not."[4]
The subject is clearly defined by Felix Klein in his "Erlangen Program" (1872): the geometry invariants of arbitrary continuous transformation, a kind of geometry. The term "topology" was introduced by Johann Benedict Listing in 1847, although he had used the term in correspondence some years earlier instead of previously used "Analysis situs". The foundation of this science, for a space of any dimension, was created by Henri Poincaré. His first article on this topic appeared in 1894.[5] In the 1930s, James Waddell Alexander II and Hassler Whitney first expressed the idea that a surface is a topological space that is locally like a Euclidean plane.
Topological spaces were first defined by Felix Hausdorff in 1914 in his seminal "Principles of Set Theory". Metric spaces had been defined earlier in 1906 by Maurice Fréchet, though it was Hausdorff who popularised the term "metric space" (German: metrischer Raum).[6][7]
Definitions[edit]
The utility of the concept of a topology is shown by the fact that there are several equivalent definitions of this mathematical structure. Thus one chooses the axiomatization suited for the application. The most commonly used is that in terms of open sets, but perhaps more intuitive is that in terms of neighbourhoods and so this is given first.
Definition via neighbourhoods[edit]
This axiomatization is due to Felix Hausdorff. Let be a (possibly empty) set. The elements of are usually called points, though they can be any mathematical object. Let be a function assigning to each (point) in a non-empty collection of subsets of The elements of will be called neighbourhoods of with respect to (or, simply, neighbourhoods of ). The function is called a neighbourhood topology if the axioms below[8] are satisfied; and then with is called a topological space.
- If is a neighbourhood of (i.e., ), then In other words, each point of the set belongs to every one of its neighbourhoods with respect to .
- If is a subset of and includes a neighbourhood of then is a neighbourhood of I.e., every superset of a neighbourhood of a point is again a neighbourhood of
- The intersection of two neighbourhoods of is a neighbourhood of
- Any neighbourhood of includes a neighbourhood of such that is a neighbourhood of each point of
The first three axioms for neighbourhoods have a clear meaning. The fourth axiom has a very important use in the structure of the theory, that of linking together the neighbourhoods of different points of
A standard example of such a system of neighbourhoods is for the real line where a subset of is defined to be a neighbourhood of a real number if it includes an open interval containing
Given such a structure, a subset of is defined to be open if is a neighbourhood of all points in The open sets then satisfy the axioms given below in the next definition of a topological space. Conversely, when given the open sets of a topological space, the neighbourhoods satisfying the above axioms can be recovered by defining to be a neighbourhood of if includes an open set such that [9]
Definition via open sets [edit]
A topology on a set X may be defined as a collection of subsets of X, called open sets and satisfying the following axioms:[10]
- The empty set and itself belong to
- Any arbitrary (finite or infinite) union of members of belongs to
- The intersection of any finite number of members of belongs to
As this definition of a topology is the most commonly used, the set of the open sets is commonly called a topology on
A subset is said to be closed in if its complement is an open set.
Examples of topologies[edit]
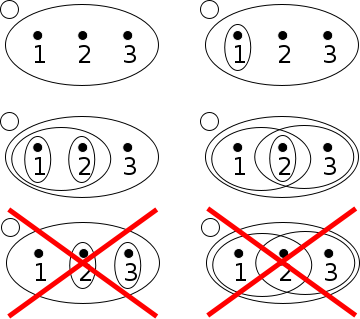
- Given the trivial or indiscrete topology on is the family consisting of only the two subsets of required by the axioms forms a topology on
- Given the family of six subsets of forms another topology of
- Given the discrete topology on is the power set of which is the family consisting of all possible subsets of In this case the topological space is called a discrete space.
- Given the set of integers, the family of all finite subsets of the integers plus itself is not a topology, because (for example) the union of all finite sets not containing zero is not finite and therefore not a member of the family of finite sets. The union of all finite sets not containing zero is also not all of and so it cannot be in
Definition via closed sets[edit]
Using de Morgan's laws, the above axioms defining open sets become axioms defining closed sets:
- The empty set and are closed.
- The intersection of any collection of closed sets is also closed.
- The union of any finite number of closed sets is also closed.
Using these axioms, another way to define a topological space is as a set together with a collection of closed subsets of Thus the sets in the topology are the closed sets, and their complements in are the open sets.
Other definitions[edit]
There are many other equivalent ways to define a topological space: in other words the concepts of neighbourhood, or that of open or closed sets can be reconstructed from other starting points and satisfy the correct axioms.
Another way to define a topological space is by using the Kuratowski closure axioms, which define the closed sets as the fixed points of an operator on the power set of
A net is a generalisation of the concept of sequence. A topology is completely determined if for every net in the set of its accumulation points is specified.
Comparison of topologies[edit]
Many topologies can be defined on a set to form a topological space. When every open set of a topology is also open for a topology one says that is finer than and is coarser than A proof that relies only on the existence of certain open sets will also hold for any finer topology, and similarly a proof that relies only on certain sets not being open applies to any coarser topology. The terms larger and smaller are sometimes used in place of finer and coarser, respectively. The terms stronger and weaker are also used in the literature, but with little agreement on the meaning, so one should always be sure of an author's convention when reading.
The collection of all topologies on a given fixed set forms a complete lattice: if is a collection of topologies on then the meet of is the intersection of and the join of is the meet of the collection of all topologies on that contain every member of
Continuous functions[edit]
A function between topological spaces is called continuous if for every and every neighbourhood of there is a neighbourhood of such that This relates easily to the usual definition in analysis. Equivalently, is continuous if the inverse image of every open set is open.[11] This is an attempt to capture the intuition that there are no "jumps" or "separations" in the function. A homeomorphism is a bijection that is continuous and whose inverse is also continuous. Two spaces are called homeomorphic if there exists a homeomorphism between them. From the standpoint of topology, homeomorphic spaces are essentially identical.[12]
In category theory, one of the fundamental categories is Top, which denotes the category of topological spaces whose objects are topological spaces and whose morphisms are continuous functions. The attempt to classify the objects of this category (up to homeomorphism) by invariants has motivated areas of research, such as homotopy theory, homology theory, and K-theory.
Examples of topological spaces[edit]
A given set may have many different topologies. If a set is given a different topology, it is viewed as a different topological space. Any set can be given the discrete topology in which every subset is open. The only convergent sequences or nets in this topology are those that are eventually constant. Also, any set can be given the trivial topology (also called the indiscrete topology), in which only the empty set and the whole space are open. Every sequence and net in this topology converges to every point of the space. This example shows that in general topological spaces, limits of sequences need not be unique. However, often topological spaces must be Hausdorff spaces where limit points are unique.
Metric spaces[edit]
Metric spaces embody a metric, a precise notion of distance between points.
Every metric space can be given a metric topology, in which the basic open sets are open balls defined by the metric. This is the standard topology on any normed vector space. On a finite-dimensional vector space this topology is the same for all norms.
There are many ways of defining a topology on the set of real numbers. The standard topology on is generated by the open intervals. The set of all open intervals forms a base or basis for the topology, meaning that every open set is a union of some collection of sets from the base. In particular, this means that a set is open if there exists an open interval of non zero radius about every point in the set. More generally, the Euclidean spaces can be given a topology. In the usual topology on the basic open sets are the open balls. Similarly, the set of complex numbers, and have a standard topology in which the basic open sets are open balls.
Other spaces[edit]
If is a filter on a set then is a topology on
Many sets of linear operators in functional analysis are endowed with topologies that are defined by specifying when a particular sequence of functions converges to the zero function.
Any local field has a topology native to it, and this can be extended to vector spaces over that field.
Every manifold has a natural topology since it is locally Euclidean. Similarly, every simplex and every simplicial complex inherits a natural topology from .
The Zariski topology is defined algebraically on the spectrum of a ring or an algebraic variety. On or the closed sets of the Zariski topology are the solution sets of systems of polynomial equations.
A linear graph has a natural topology that generalizes many of the geometric aspects of graphs with vertices and edges.
The Sierpiński space is the simplest non-discrete topological space. It has important relations to the theory of computation and semantics.
There exist numerous topologies on any given finite set. Such spaces are called finite topological spaces. Finite spaces are sometimes used to provide examples or counterexamples to conjectures about topological spaces in general.
Any set can be given the cofinite topology in which the open sets are the empty set and the sets whose complement is finite. This is the smallest T1 topology on any infinite set.[13]
Any set can be given the cocountable topology, in which a set is defined as open if it is either empty or its complement is countable. When the set is uncountable, this topology serves as a counterexample in many situations.
The real line can also be given the lower limit topology. Here, the basic open sets are the half open intervals This topology on is strictly finer than the Euclidean topology defined above; a sequence converges to a point in this topology if and only if it converges from above in the Euclidean topology. This example shows that a set may have many distinct topologies defined on it.
If is an ordinal number, then the set may be endowed with the order topology generated by the intervals and where and are elements of
Outer space of a free group consists of the so-called "marked metric graph structures" of volume 1 on [14]
Topological constructions[edit]
Every subset of a topological space can be given the subspace topology in which the open sets are the intersections of the open sets of the larger space with the subset. For any indexed family of topological spaces, the product can be given the product topology, which is generated by the inverse images of open sets of the factors under the projection mappings. For example, in finite products, a basis for the product topology consists of all products of open sets. For infinite products, there is the additional requirement that in a basic open set, all but finitely many of its projections are the entire space.
A quotient space is defined as follows: if is a topological space and is a set, and if is a surjective function, then the quotient topology on is the collection of subsets of that have open inverse images under In other words, the quotient topology is the finest topology on for which is continuous. A common example of a quotient topology is when an equivalence relation is defined on the topological space The map is then the natural projection onto the set of equivalence classes.
The Vietoris topology on the set of all non-empty subsets of a topological space named for Leopold Vietoris, is generated by the following basis: for every -tuple of open sets in we construct a basis set consisting of all subsets of the union of the that have non-empty intersections with each
The Fell topology on the set of all non-empty closed subsets of a locally compact Polish space is a variant of the Vietoris topology, and is named after mathematician James Fell. It is generated by the following basis: for every -tuple of open sets in and for every compact set the set of all subsets of that are disjoint from and have nonempty intersections with each is a member of the basis.
Classification of topological spaces[edit]
Topological spaces can be broadly classified, up to homeomorphism, by their topological properties. A topological property is a property of spaces that is invariant under homeomorphisms. To prove that two spaces are not homeomorphic it is sufficient to find a topological property not shared by them. Examples of such properties include connectedness, compactness, and various separation axioms. For algebraic invariants see algebraic topology.
Topological spaces with algebraic structure[edit]
For any algebraic objects we can introduce the discrete topology, under which the algebraic operations are continuous functions. For any such structure that is not finite, we often have a natural topology compatible with the algebraic operations, in the sense that the algebraic operations are still continuous. This leads to concepts such as topological groups, topological vector spaces, topological rings and local fields.
Topological spaces with order structure[edit]
- Spectral: A space is spectral if and only if it is the prime spectrum of a ring (Hochster theorem).
- Specialization preorder: In a space the specialization preorder (or canonical preorder) is defined by if and only if where denotes an operator satisfying the Kuratowski closure axioms.
See also[edit]
- Complete Heyting algebra – The system of all open sets of a given topological space ordered by inclusion is a complete Heyting algebra.
- Compact space – Type of mathematical space
- Convergence space – Generalization of the notion of convergence that is found in general topology
- Exterior space
- Hausdorff space – Type of topological space
- Hilbert space – Type of topological vector space
- Hemicontinuity
- Linear subspace – In mathematics, vector subspace
- Quasitopological space – a set X equipped with a function that associates to every compact Hausdorff space K a collection of maps K→C satisfying certain natural conditions
- Relatively compact subspace – subset of a topological space whose closure is compact
- Space (mathematics) – Mathematical set with some added structure
Citations[edit]
- ^ Schubert 1968, p. 13
- ^ Sutherland, W. A. (1975). Introduction to metric and topological spaces. Oxford [England]: Clarendon Press. ISBN 0-19-853155-9. OCLC 1679102.
- ^ Gauss 1827.
- ^ a b Gallier & Xu 2013.
- ^ J. Stillwell, Mathematics and its history
- ^ "metric space". Oxford English Dictionary (Online ed.). Oxford University Press. (Subscription or participating institution membership required.)
- ^
Hausdorff, Felix (1914) [1914]. "Punktmengen in allgemeinen Räumen". Grundzüge der Mengenlehre. Göschens Lehrbücherei/Gruppe I: Reine und Angewandte Mathematik Serie (in German). Leipzig: Von Veit (published 2011). p. 211. ISBN 9783110989854. Retrieved 20 August 2022.
Unter einem m e t r i s c h e n R a u m e verstehen wir eine Menge E, [...].
- ^ Brown 2006, section 2.1.
- ^ Brown 2006, section 2.2.
- ^ Armstrong 1983, definition 2.1.
- ^ Armstrong 1983, theorem 2.6.
- ^ Munkres, James R (2015). Topology. Pearson. pp. 317–319. ISBN 978-93-325-4953-1.
- ^ Anderson, B. A.; Stewart, D. G. (1969). "-complements of topologies". Proceedings of the American Mathematical Society. 23: 77–81. doi:10.2307/2037491. JSTOR 2037491. MR 0244927.
- ^ Culler, Marc; Vogtmann, Karen (1986). "Moduli of graphs and automorphisms of free groups" (PDF). Inventiones Mathematicae. 84 (1): 91–119. Bibcode:1986InMat..84...91C. doi:10.1007/BF01388734. S2CID 122869546.
Bibliography[edit]
- Armstrong, M. A. (1983) [1979]. Basic Topology. Undergraduate Texts in Mathematics. Springer. ISBN 0-387-90839-0.
- Bredon, Glen E., Topology and Geometry (Graduate Texts in Mathematics), Springer; 1st edition (October 17, 1997). ISBN 0-387-97926-3.
- Bourbaki, Nicolas; Elements of Mathematics: General Topology, Addison-Wesley (1966).
- Brown, Ronald (2006). Topology and Groupoids. Booksurge. ISBN 1-4196-2722-8. (3rd edition of differently titled books)
- Čech, Eduard; Point Sets, Academic Press (1969).
- Fulton, William, Algebraic Topology, (Graduate Texts in Mathematics), Springer; 1st edition (September 5, 1997). ISBN 0-387-94327-7.
- Gallier, Jean; Xu, Dianna (2013). A Guide to the Classification Theorem for Compact Surfaces. Springer.
- Gauss, Carl Friedrich (1827). General investigations of curved surfaces.
- Lipschutz, Seymour; Schaum's Outline of General Topology, McGraw-Hill; 1st edition (June 1, 1968). ISBN 0-07-037988-2.
- Munkres, James; Topology, Prentice Hall; 2nd edition (December 28, 1999). ISBN 0-13-181629-2.
- Runde, Volker; A Taste of Topology (Universitext), Springer; 1st edition (July 6, 2005). ISBN 0-387-25790-X.
- Schubert, Horst (1968), Topology, Macdonald Technical & Scientific, ISBN 0-356-02077-0
- Steen, Lynn A. and Seebach, J. Arthur Jr.; Counterexamples in Topology, Holt, Rinehart and Winston (1970). ISBN 0-03-079485-4.
- Vaidyanathaswamy, R. (1960). Set Topology. Chelsea Publishing Co. ISBN 0486404560.
- Willard, Stephen (2004). General Topology. Dover Publications. ISBN 0-486-43479-6.
External links[edit]
- "Topological space", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
















































































