Radiation pressure
Radiation pressure (also known as light pressure) is mechanical pressure exerted upon a surface due to the exchange of momentum between the object and the electromagnetic field. This includes the momentum of light or electromagnetic radiation of any wavelength that is absorbed, reflected, or otherwise emitted (e.g. black-body radiation) by matter on any scale (from macroscopic objects to dust particles to gas molecules).[1][2][3] The associated force is called the radiation pressure force, or sometimes just the force of light.
The forces generated by radiation pressure are generally too small to be noticed under everyday circumstances; however, they are important in some physical processes and technologies. This particularly includes objects in outer space, where it is usually the main force acting on objects besides gravity, and where the net effect of a tiny force may have a large cumulative effect over long periods of time. For example, had the effects of the Sun's radiation pressure on the spacecraft of the Viking program been ignored, the spacecraft would have missed Mars orbit by about 15,000 km (9,300 mi).[4] Radiation pressure from starlight is crucial in a number of astrophysical processes as well. The significance of radiation pressure increases rapidly at extremely high temperatures and can sometimes dwarf the usual gas pressure, for instance, in stellar interiors and thermonuclear weapons. Furthermore, large lasers operating in space have been suggested as a means of propelling sail craft in beam-powered propulsion.
Radiation pressure forces are the bedrock of laser technology and the branches of science that rely heavily on lasers and other optical technologies. That includes, but is not limited to, biomicroscopy (where light is used to irradiate and observe microbes, cells, and molecules), quantum optics, and optomechanics (where light is used to probe and control objects like atoms, qubits and macroscopic quantum objects). Direct applications of the radiation pressure force in these fields are, for example, laser cooling (the subject of the 1997 Nobel Prize in Physics),[5] quantum control of macroscopic objects and atoms (2012 Nobel Prize in Physics),[6] interferometry (2017 Nobel Prize in Physics)[7] and optical tweezers (2018 Nobel Prize in Physics).[8]
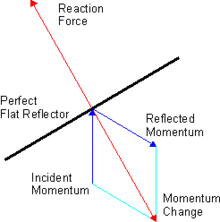
Radiation pressure can equally well be accounted for by considering the momentum of a classical electromagnetic field or in terms of the momenta of photons, particles of light. The interaction of electromagnetic waves or photons with matter may involve an exchange of momentum. Due to the law of conservation of momentum, any change in the total momentum of the waves or photons must involve an equal and opposite change in the momentum of the matter it interacted with (Newton's third law of motion), as is illustrated in the accompanying figure for the case of light being perfectly reflected by a surface. This transfer of momentum is the general explanation for what we term radiation pressure.
Discovery
[edit]
Johannes Kepler put forward the concept of radiation pressure in 1619 to explain the observation that a tail of a comet always points away from the Sun.[9]
The assertion that light, as electromagnetic radiation, has the property of momentum and thus exerts a pressure upon any surface that is exposed to it was published by James Clerk Maxwell in 1862, and proven experimentally by Russian physicist Pyotr Lebedev in 1900[10] and by Ernest Fox Nichols and Gordon Ferrie Hull in 1901.[11] The pressure is very small, but can be detected by allowing the radiation to fall upon a delicately poised vane of reflective metal in a Nichols radiometer (this should not be confused with the Crookes radiometer, whose characteristic motion is not caused by radiation pressure but by air flow caused by temperature differentials.)
Theory
[edit]Radiation pressure can be viewed as a consequence of the conservation of momentum given the momentum attributed to electromagnetic radiation. That momentum can be equally well calculated on the basis of electromagnetic theory or from the combined momenta of a stream of photons, giving identical results as is shown below.
Radiation pressure from momentum of an electromagnetic wave
[edit]According to Maxwell's theory of electromagnetism, an electromagnetic wave carries momentum. Momentum will be transferred to any surface it strikes that absorbs or reflects the radiation.
Consider the momentum transferred to a perfectly absorbing (black) surface. The energy flux (irradiance) of a plane wave is calculated using the Poynting vector , which is the cross product of the electric field vector E and the magnetic field's auxiliary field vector (or magnetizing field) H. The magnitude, denoted by S, divided by the speed of light is the density of the linear momentum per unit area (pressure) of the electromagnetic field. So, dimensionally, the Poynting vector is S = power/area = rate of doing work/area = ΔF/Δt Δx/area, which is the speed of light, c = Δx / Δt, times pressure, ΔF / area. That pressure is experienced as radiation pressure on the surface: where is pressure (usually in pascals), is the incident irradiance (usually in W/m2) and is the speed of light in vacuum. Here, 1/c ≈ 3.34 N/GW.
If the surface is planar at an angle α to the incident wave, the intensity across the surface will be geometrically reduced by the cosine of that angle and the component of the radiation force against the surface will also be reduced by the cosine of α, resulting in a pressure:
The momentum from the incident wave is in the same direction of that wave. But only the component of that momentum normal to the surface contributes to the pressure on the surface, as given above. The component of that force tangent to the surface is not called pressure.[12]
Radiation pressure from reflection
[edit]The above treatment for an incident wave accounts for the radiation pressure experienced by a black (totally absorbing) body. If the wave is specularly reflected, then the recoil due to the reflected wave will further contribute to the radiation pressure. In the case of a perfect reflector, this pressure will be identical to the pressure caused by the incident wave:
thus doubling the net radiation pressure on the surface:
For a partially reflective surface, the second term must be multiplied by the reflectivity (also known as reflection coefficient of intensity), so that the increase is less than double. For a diffusely reflective surface, the details of the reflection and geometry must be taken into account, again resulting in an increased net radiation pressure of less than double.
Radiation pressure by emission
[edit]Just as a wave reflected from a body contributes to the net radiation pressure experienced, a body that emits radiation of its own (rather than reflected) obtains a radiation pressure again given by the irradiance of that emission in the direction normal to the surface Ie:
The emission can be from black-body radiation or any other radiative mechanism. Since all materials emit black-body radiation (unless they are totally reflective or at absolute zero), this source for radiation pressure is ubiquitous but usually tiny. However, because black-body radiation increases rapidly with temperature (as the fourth power of temperature, given by the Stefan–Boltzmann law), radiation pressure due to the temperature of a very hot object (or due to incoming black-body radiation from similarly hot surroundings) can become significant. This is important in stellar interiors.
Radiation pressure in terms of photons
[edit]Electromagnetic radiation can be viewed in terms of particles rather than waves; these particles are known as photons. Photons do not have a rest-mass; however, photons are never at rest (they move at the speed of light) and acquire a momentum nonetheless which is given by: where p is momentum, h is the Planck constant, λ is wavelength, and c is speed of light in vacuum. And Ep is the energy of a single photon given by:
The radiation pressure again can be seen as the transfer of each photon's momentum to the opaque surface, plus the momentum due to a (possible) recoil photon for a (partially) reflecting surface. Since an incident wave of irradiance If over an area A has a power of IfA, this implies a flux of If/Ep photons per second per unit area striking the surface. Combining this with the above expression for the momentum of a single photon, results in the same relationships between irradiance and radiation pressure described above using classical electromagnetics. And again, reflected or otherwise emitted photons will contribute to the net radiation pressure identically.
Compression in a uniform radiation field
[edit]In general, the pressure of electromagnetic waves can be obtained from the vanishing of the trace of the electromagnetic stress tensor: since this trace equals 3P − u, we get where u is the radiation energy per unit volume.
This can also be shown in the specific case of the pressure exerted on surfaces of a body in thermal equilibrium with its surroundings, at a temperature T: the body will be surrounded by a uniform radiation field described by the Planck black-body radiation law and will experience a compressive pressure due to that impinging radiation, its reflection, and its own black-body emission. From that it can be shown that the resulting pressure is equal to one third of the total radiant energy per unit volume in the surrounding space.[13][14][15][16]
By using Stefan–Boltzmann law, this can be expressed as where is the Stefan–Boltzmann constant.
Solar radiation pressure
[edit]Solar radiation pressure is due to the Sun's radiation at closer distances, thus especially within the Solar System. (The radiation pressure of sunlight on Earth is very small: it is equivalent to that exerted by the weight of about a milligram on an area of 1 square metre, or 10 μN/m2.)[citation needed] While it acts on all objects, its net effect is generally greater on smaller bodies, since they have a larger ratio of surface area to mass. All spacecraft experience such a pressure, except when they are behind the shadow of a larger orbiting body.
Solar radiation pressure on objects near the Earth may be calculated using the Sun's irradiance at 1 AU, known as the solar constant, or GSC, whose value is set at 1361 W/m2 as of 2011.[17]
All stars have a spectral energy distribution that depends on their surface temperature. The distribution is approximately that of black-body radiation. This distribution must be taken into account when calculating the radiation pressure or identifying reflector materials for optimizing a solar sail, for instance.
Momentary or hours long solar pressures can indeed escalate due to release of solar flares and coronal mass ejections, but effects remain essentially immeasureable in relation to Earth's orbit. However these pressures persist over eons, such that cumulatively having produced a measureable movement on the Earth-Moon system's orbit.
Pressures of absorption and reflection
[edit]Solar radiation pressure at the Earth's distance from the Sun, may be calculated by dividing the solar constant GSC (above) by the speed of light c. For an absorbing sheet facing the Sun, this is simply:[18]
This result is in pascals, equivalent to N/m2 (newtons per square meter). For a sheet at an angle α to the Sun, the effective area A of a sheet is reduced by a geometrical factor resulting in a force in the direction of the sunlight of:
To find the component of this force normal to the surface, another cosine factor must be applied resulting in a pressure P on the surface of:
Note, however, that in order to account for the net effect of solar radiation on a spacecraft for instance, one would need to consider the total force (in the direction away from the Sun) given by the preceding equation, rather than just the component normal to the surface that we identify as "pressure".
The solar constant is defined for the Sun's radiation at the distance to the Earth, also known as one astronomical unit (au). Consequently, at a distance of R astronomical units (R thus being dimensionless), applying the inverse-square law, we would find:
Finally, considering not an absorbing but a perfectly reflecting surface, the pressure is doubled due to the reflected wave, resulting in:
Note that unlike the case of an absorbing material, the resulting force on a reflecting body is given exactly by this pressure acting normal to the surface, with the tangential forces from the incident and reflecting waves canceling each other. In practice, materials are neither totally reflecting nor totally absorbing, so the resulting force will be a weighted average of the forces calculated using these formulas.
| Distance from Sun | Radiation pressure in μPa (μN/m2) |
|---|---|
| 0.20 au | 227 |
| 0.39 au (Mercury) | 59.7 |
| 0.72 au (Venus) | 17.5 |
| 1.00 au (Earth) | 9.08 |
| 1.52 au (Mars) | 3.93 |
| 3.00 au (typical asteroid) | 1.01 |
| 5.20 au (Jupiter) | 0.34 |
Radiation pressure perturbations
[edit]Solar radiation pressure is a source of orbital perturbations. It significantly affects the orbits and trajectories of small bodies including all spacecraft.
Solar radiation pressure affects bodies throughout much of the Solar System. Small bodies are more affected than large ones because of their lower mass relative to their surface area. Spacecraft are affected along with natural bodies (comets, asteroids, dust grains, gas molecules).
The radiation pressure results in forces and torques on the bodies that can change their translational and rotational motions. Translational changes affect the orbits of the bodies. Rotational rates may increase or decrease. Loosely aggregated bodies may break apart under high rotation rates. Dust grains can either leave the Solar System or spiral into the Sun.[19]
A whole body is typically composed of numerous surfaces that have different orientations on the body. The facets may be flat or curved. They will have different areas. They may have optical properties differing from other aspects.
At any particular time, some facets are exposed to the Sun, and some are in shadow. Each surface exposed to the Sun is reflecting, absorbing, and emitting radiation. Facets in shadow are emitting radiation. The summation of pressures across all of the facets defines the net force and torque on the body. These can be calculated using the equations in the preceding sections.[12][18]
The Yarkovsky effect affects the translation of a small body. It results from a face leaving solar exposure being at a higher temperature than a face approaching solar exposure. The radiation emitted from the warmer face is more intense than that of the opposite face, resulting in a net force on the body that affects its motion.[20]
The YORP effect is a collection of effects expanding upon the earlier concept of the Yarkovsky effect, but of a similar nature. It affects the spin properties of bodies.[citation needed]
The Poynting–Robertson effect applies to grain-size particles. From the perspective of a grain of dust circling the Sun, the Sun's radiation appears to be coming from a slightly forward direction (aberration of light). Therefore, the absorption of this radiation leads to a force with a component against the direction of movement. (The angle of aberration is tiny, since the radiation is moving at the speed of light, while the dust grain is moving many orders of magnitude slower than that.) The result is a gradual spiral of dust grains into the Sun. Over long periods of time, this effect cleans out much of the dust in the Solar System.
While rather small in comparison to other forces, the radiation pressure force is inexorable. Over long periods of time, the net effect of the force is substantial. Such feeble pressures can produce marked effects upon minute particles like gas ions and electrons, and are essential in the theory of electron emission from the Sun, of cometary material, and so on.
Because the ratio of surface area to volume (and thus mass) increases with decreasing particle size, dusty (micrometre-size) particles are susceptible to radiation pressure even in the outer Solar System. For example, the evolution of the outer rings of Saturn is significantly influenced by radiation pressure.
As a consequence of light pressure, Einstein[21] in 1909 predicted the existence of "radiation friction", which would oppose the movement of matter. He wrote: "radiation will exert pressure on both sides of the plate. The forces of pressure exerted on the two sides are equal if the plate is at rest. However, if it is in motion, more radiation will be reflected on the surface that is ahead during the motion (front surface) than on the back surface. The backward acting force of pressure exerted on the front surface is thus larger than the force of pressure acting on the back. Hence, as the resultant of the two forces, there remains a force that counteracts the motion of the plate and that increases with the velocity of the plate. We will call this resultant 'radiation friction' in brief."
Solar sails
[edit]Solar sailing, an experimental method of spacecraft propulsion, uses radiation pressure from the Sun as a motive force. The idea of interplanetary travel by light was mentioned by Jules Verne in his 1865 novel From the Earth to the Moon.
A sail reflects about 90% of the incident radiation. The 10% that is absorbed is radiated away from both surfaces, with the proportion emitted from the unlit surface depending on the thermal conductivity of the sail. A sail has curvature, surface irregularities, and other minor factors that affect its performance.
The Japan Aerospace Exploration Agency (JAXA) has successfully unfurled a solar sail in space, which has already succeeded in propelling its payload with the IKAROS project.
Cosmic effects of radiation pressure
[edit]Radiation pressure has had a major effect on the development of the cosmos, from the birth of the universe to ongoing formation of stars and shaping of clouds of dust and gasses on a wide range of scales.[22]
Early universe
[edit]The photon epoch is a phase when the energy of the universe was dominated by photons, between 10 seconds and 380,000 years after the Big Bang.[23]
Galaxy formation and evolution
[edit]
The process of galaxy formation and evolution began early in the history of the cosmos. Observations of the early universe strongly suggest that objects grew from bottom-up (i.e., smaller objects merging to form larger ones). As stars are thereby formed and become sources of electromagnetic radiation, radiation pressure from the stars becomes a factor in the dynamics of remaining circumstellar material.[24]
Clouds of dust and gases
[edit]The gravitational compression of clouds of dust and gases is strongly influenced by radiation pressure, especially when the condensations lead to star births. The larger young stars forming within the compressed clouds emit intense levels of radiation that shift the clouds, causing either dispersion or condensations in nearby regions, which influences birth rates in those nearby regions.
Clusters of stars
[edit]Stars predominantly form in regions of large clouds of dust and gases, giving rise to star clusters. Radiation pressure from the member stars eventually disperses the clouds, which can have a profound effect on the evolution of the cluster.
Many open clusters are inherently unstable, with a small enough mass that the escape velocity of the system is lower than the average velocity of the constituent stars. These clusters will rapidly disperse within a few million years. In many cases, the stripping away of the gas from which the cluster formed by the radiation pressure of the hot young stars reduces the cluster mass enough to allow rapid dispersal.

Star formation
[edit]Star formation is the process by which dense regions within molecular clouds in interstellar space collapse to form stars. As a branch of astronomy, star formation includes the study of the interstellar medium and giant molecular clouds (GMC) as precursors to the star formation process, and the study of protostars and young stellar objects as its immediate products. Star formation theory, as well as accounting for the formation of a single star, must also account for the statistics of binary stars and the initial mass function.
Stellar planetary systems
[edit]Planetary systems are generally believed to form as part of the same process that results in star formation. A protoplanetary disk forms by gravitational collapse of a molecular cloud, called a solar nebula, and then evolves into a planetary system by collisions and gravitational capture. Radiation pressure can clear a region in the immediate vicinity of the star. As the formation process continues, radiation pressure continues to play a role in affecting the distribution of matter. In particular, dust and grains can spiral into the star or escape the stellar system under the action of radiation pressure.

Stellar interiors
[edit]In stellar interiors the temperatures are very high. Stellar models predict a temperature of 15 MK in the center of the Sun, and at the cores of supergiant stars the temperature may exceed 1 GK. As the radiation pressure scales as the fourth power of the temperature, it becomes important at these high temperatures. In the Sun, radiation pressure is still quite small when compared to the gas pressure. In the heaviest non-degenerate stars, radiation pressure is the dominant pressure component.[25]
Comets
[edit]Solar radiation pressure strongly affects comet tails. Solar heating causes gases to be released from the comet nucleus, which also carry away dust grains. Radiation pressure and solar wind then drive the dust and gases away from the Sun's direction. The gases form a generally straight tail, while slower moving dust particles create a broader, curving tail.
Laser applications of radiation pressure
[edit]Optical tweezers
[edit]Lasers can be used as a source of monochromatic light with wavelength . With a set of lenses, one can focus the laser beam to a point that is in diameter (or ).
The radiation pressure of a P = 30 mW laser with λ = 1064 nm can therefore be computed as follows.
Area:
force:
pressure:
This is used to trap or levitate particles in optical tweezers.
Light–matter interactions
[edit]
The reflection of a laser pulse from the surface of an elastic solid can give rise to various types of elastic waves that propagate inside the solid or liquid. In other words, the light can excite and/or amplify motion of, and in, materials. This is the subject of study in the field of optomechanics. The weakest waves are generally those that are generated by the radiation pressure acting during the reflection of the light. Such light-pressure-induced elastic waves have for example observed inside an ultrahigh-reflectivity dielectric mirror.[26] These waves are the most basic fingerprint of a light-solid matter interaction on the macroscopic scale.[27] In the field of cavity optomechanics, light is trapped and resonantly enhanced in optical cavities, for example between mirrors. This serves the purpose of gravely enhancing the power of the light, and the radiation pressure it can exert on objects and materials. Optical control (that is, manipulation of the motion) of a plethora of objects has been realized: from kilometers long beams (such as in the LIGO interferometer)[28] to clouds of atoms,[29] and from micro-engineered trampolines[30] to superfluids.[31][32]
Opposite to exciting or amplifying motion, light can also damp the motion of objects. Laser cooling is a method of cooling materials very close to absolute zero by converting some of material's motional energy into light. Kinetic energy and thermal energy of the material are synonyms here, because they represent the energy associated with Brownian motion of the material. Atoms traveling towards a laser light source perceive a doppler effect tuned to the absorption frequency of the target element. The radiation pressure on the atom slows movement in a particular direction until the Doppler effect moves out of the frequency range of the element, causing an overall cooling effect.[34]
An other active research area of laser–matter interaction is the radiation pressure acceleration of ions or protons from thin–foil targets.[35] High ion energy beams can be generated for medical applications (for example in ion beam therapy[36]) by the radiation pressure of short laser pulses on ultra-thin foils.
See also
[edit]References
[edit]- ^ Stellar Atmospheres, D. Mihalas (1978), Second edition, W. H. Freeman & Co.
- ^ Eddington, A. S., & Eddington, A. S. (1988). The internal constitution of the stars. Cambridge University Press.
- ^ Chandrasekhar, S. (2013). Radiative transfer. Courier Corporation.
- ^ Eugene Hecht, "Optics", 4th edition, p. 57.
- ^ Cohen-Tannoudji, Claude N. (1998-07-01). "Nobel Lecture: Manipulating atoms with photons". Reviews of Modern Physics. 70 (3): 707–719. Bibcode:1998RvMP...70..707C. doi:10.1103/RevModPhys.70.707. ISSN 0034-6861.
- ^ Wineland, David J. (2013-07-12). "Nobel Lecture: Superposition, entanglement, and raising Schrödinger's cat". Reviews of Modern Physics. 85 (3): 1103–1114. Bibcode:2013RvMP...85.1103W. doi:10.1103/RevModPhys.85.1103. ISSN 0034-6861.
- ^ Weiss, Rainer (2018-12-18). "Nobel Lecture: LIGO and the discovery of gravitational waves I". Reviews of Modern Physics. 90 (4): 040501. Bibcode:2018RvMP...90d0501W. doi:10.1103/RevModPhys.90.040501.
- ^ Schirber, Michael (2018-10-04). "Nobel Prize—Lasers as Tools". Physics. 11: 100. Bibcode:2018PhyOJ..11..100S. doi:10.1103/physics.11.100. S2CID 125788399.
- ^ Johannes Kepler (1619). De Cometis Libelli Tres.
- ^ P. Lebedew, 1901, "Untersuchungen über die Druckkräfte des Lichtes", Annalen der Physik, 1901 Series 4 6, 433-458.
- ^ Nichols, E. F & Hull, G. F. (1903) The Pressure due to Radiation, The Astrophysical Journal, Vol.17 No.5, p.315-351
- ^ a b Wright, Jerome L. (1992), Space Sailing, Gordon and Breach Science Publishers
- ^ Shankar R. Principles of Quantum Mechanics (PDF) (2nd ed.).
- ^ Carroll, Bradley W; Dale A. Ostlie. An Introduction to Modern Astrophysics (2nd ed.).
- ^ Jackson, John David (1999). Classical Electrodynamics.
- ^ Kardar, Mehran. "Statistical Physics of Particles".
- ^ Kopp, G.; Lean, J. L. (2011). "A new, lower value of total solar irradiance: Evidence and climate significance". Geophysical Research Letters. 38 (1): n/a. Bibcode:2011GeoRL..38.1706K. doi:10.1029/2010GL045777.
- ^ a b Georgevic, R. M. (1973) "The Solar Radiation Pressure Forces and Torques Model", The Journal of the Astronautical Sciences, Vol. 27, No. 1, Jan–Feb. First known publication describing how solar radiation pressure creates forces and torques that affect spacecraft.
- ^ Center, NASA's Goddard Space Flight. "Dust models paint alien's view of the solar system (w/ Video)". phys.org. Retrieved 2022-03-01.
- ^ Vokrouhlicky, David; Bottke, William F. (2012-05-02). "Yarkovsky and YORP effects". Scholarpedia. 7 (5): 10599. arXiv:1502.01249. Bibcode:2012SchpJ...710599B. doi:10.4249/scholarpedia.10599. ISSN 1941-6016.
- ^ Einstein, A. (1989). On the development of our views concerning the nature and constitution of radiation. Translated in: The Collected Papers of Albert Einstein. Vol. 2. Princeton, New Jersey: Princeton University Press. p. 391.
- ^ Karel Velan, A. (1992), "The Birth of the First Generation of Stars", The Multi-Universe Cosmos, Springer US, pp. 267–278, doi:10.1007/978-1-4684-6030-8_22, ISBN 9781468460322
- ^ The early universe. Unruh, W. G., Semenoff, G. W., North Atlantic Treaty Organization. Scientific Affairs Division. Dordrecht: D. Reidel. 1988. ISBN 9027726191. OCLC 16684785.
{{cite book}}: CS1 maint: others (link) - ^ Longair, Malcolm S., 1941– (2008). Galaxy formation. Springer. ISBN 9783540734772. OCLC 212409895.
{{cite book}}: CS1 maint: multiple names: authors list (link) CS1 maint: numeric names: authors list (link) - ^ Dale A. Ostlie and Bradley W. Carroll, An Introduction to Modern Astrophysics (2nd edition), page 341, Pearson, San Francisco, 2007
- ^ Požar, T.; Možina, J. (2013). "Measurement of Elastic Waves Induced by the Reflection of Light". Physical Review Letters. 111 (18): 185501. Bibcode:2013PhRvL.111r5501P. doi:10.1103/Physrevlett.111.185501. PMID 24237537.
- ^ Požar, T.; Laloš, J.; Babnik, A.; Petkovšek, R.; Bethune-Waddell, M.; Chau, K. J.; Lukasievicz, G. V. B.; Astrath, N. G. C. (2018). "Isolated detection of elastic waves driven by the momentum of light". Nature Communications. 9 (1): 3340. Bibcode:2018NatCo...9.3340P. doi:10.1038/s41467-018-05706-3. PMC 6105914. PMID 30131489.
- ^ Johnston, Hamish (10 Dec 2019). "Quantum squeezing boosts performance of LIGO and Virgo gravitational-wave detectors". PhysicsWorld.
- ^ Schreppler, Sydney; Spethmann, Nicolas; Brahms, Nathan; Botter, Thierry; Barrios, Maryrose; Stamper-Kurn, Dan M. (2014-06-27). "Optically measuring force near the standard quantum limit". Science. 344 (6191): 1486–1489. arXiv:1312.4896. Bibcode:2014Sci...344.1486S. doi:10.1126/science.1249850. ISSN 0036-8075. PMID 24970079. S2CID 206554506.
- ^ Kleckner, Dustin; Marshall, William; de Dood, Michiel J. A.; Dinyari, Khodadad Nima; Pors, Bart-Jan; Irvine, William T. M.; Bouwmeester, Dirk (2006-05-02). "High Finesse Opto-Mechanical Cavity with a Movable Thirty-Micron-Size Mirror". Physical Review Letters. 96 (17): 173901. Bibcode:2006PhRvL..96q3901K. doi:10.1103/PhysRevLett.96.173901. hdl:1887/65506. PMID 16712296. S2CID 1801710.
- ^ Harris, G. I.; McAuslan, D. L.; Sheridan, E.; Sachkou, Y.; Baker, C.; Bowen, W. P. (2016). "Laser cooling and control of excitations in superfluid helium". Nature Physics. 12 (8): 788–793. arXiv:1506.04542. Bibcode:2016NatPh..12..788H. doi:10.1038/nphys3714. ISSN 1745-2481. S2CID 118135792.
- ^ Kashkanova, A. D.; Shkarin, A. B.; Brown, C. D.; Flowers-Jacobs, N. E.; Childress, L.; Hoch, S. W.; Hohmann, L.; Ott, K.; Reichel, J.; Harris, J. G. E. (2017). "Superfluid Brillouin optomechanics". Nature Physics. 13 (1): 74–79. arXiv:1602.05640. Bibcode:2017NatPh..13...74K. doi:10.1038/nphys3900. ISSN 1745-2481. S2CID 10880961.
- ^ Yu, Wenyan; Jiang, Wei C.; Lin, Qiang; Lu, Tao (2016-07-27). "Cavity optomechanical spring sensing of single molecules". Nature Communications. 7 (1): 12311. arXiv:1504.03727. Bibcode:2016NatCo...712311Y. doi:10.1038/ncomms12311. ISSN 2041-1723. PMC 4974467. PMID 27460277.
- ^ Aspelmeyer, Markus; Kippenberg, Tobias J.; Marquardt, Florian (2014-12-30). "Cavity optomechanics". Reviews of Modern Physics. 86 (4): 1391–1452. arXiv:1303.0733. Bibcode:2014RvMP...86.1391A. doi:10.1103/RevModPhys.86.1391. S2CID 119252645.
- ^ Meinhold, Tim Arniko; Kumar, Naveen (December 2021). "Radiation pressure acceleration of protons from structured thin-foil targets". Journal of Plasma Physics. 87 (6): 905870607. arXiv:2111.14087. Bibcode:2021JPlPh..87f9007M. doi:10.1017/S0022377821001070. ISSN 0022-3778. S2CID 244636880.
- ^ Malka, Victor; Fritzler, Sven; Lefebvre, Erik; d'Humières, Emmanuel; Ferrand, Régis; Grillon, Georges; Albaret, Claude; Meyroneinc, Samuel; Chambaret, Jean-Paul; Antonetti, Andre; Hulin, Danièle (2004-05-27). "Practicability of protontherapy using compact laser systems". Medical Physics. 31 (6): 1587–1592. Bibcode:2004MedPh..31.1587M. doi:10.1118/1.1747751. PMID 15259663.
Further reading
[edit]- Demir, Dilek, "A table-top demonstration of radiation pressure", 2011, Diplomathesis, E-Theses univie
























