Stericated 7-simplexes
 7-simplex |
 Stericated 7-simplex |
 Bistericated 7-simplex |
 Steritruncated 7-simplex |
 Bisteritruncated 7-simplex |
 Stericantellated 7-simplex |
 Bistericantellated 7-simplex |
 Stericantitruncated 7-simplex |
 Bistericantitruncated 7-simplex |
 Steriruncinated 7-simplex |
 Steriruncitruncated 7-simplex |
 Steriruncicantellated 7-simplex |
 Bisteriruncitruncated 7-simplex |
 Steriruncicantitruncated 7-simplex |
 Bisteriruncicantitruncated 7-simplex |
In seven-dimensional geometry, a stericated 7-simplex is a convex uniform 7-polytope with 4th order truncations (sterication) of the regular 7-simplex.
There are 14 unique sterication for the 7-simplex with permutations of truncations, cantellations, and runcinations.
Stericated 7-simplex
[edit]| Stericated 7-simplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t0,4{3,3,3,3,3,3} |
| Coxeter-Dynkin diagrams | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 2240 |
| Vertices | 280 |
| Vertex figure | |
| Coxeter group | A7, [36], order 40320 |
| Properties | convex |
Alternate names
[edit]- Small cellated octaexon (acronym: sco) (Jonathan Bowers)[1]
Coordinates
[edit]The vertices of the stericated 7-simplex can be most simply positioned in 8-space as permutations of (0,0,0,1,1,1,1,2). This construction is based on facets of the stericated 8-orthoplex.
Images
[edit]| Ak Coxeter plane | A7 | A6 | A5 |
|---|---|---|---|
| Graph | 
|
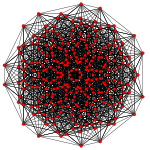
|

|
| Dihedral symmetry | [8] | [7] | [6] |
| Ak Coxeter plane | A4 | A3 | A2 |
| Graph | 
|

|

|
| Dihedral symmetry | [5] | [4] | [3] |
Bistericated 7-simplex
[edit]| bistericated 7-simplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t1,5{3,3,3,3,3,3} |
| Coxeter-Dynkin diagrams | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 3360 |
| Vertices | 420 |
| Vertex figure | |
| Coxeter group | A7×2, [[36]], order 80320 |
| Properties | convex |
Alternate names
[edit]- Small bicellated hexadecaexon (acronym: sabach) (Jonathan Bowers)[2]
Coordinates
[edit]The vertices of the bistericated 7-simplex can be most simply positioned in 8-space as permutations of (0,0,1,1,1,1,2,2). This construction is based on facets of the bistericated 8-orthoplex.
Images
[edit]| Ak Coxeter plane | A7 | A6 | A5 |
|---|---|---|---|
| Graph | 
|
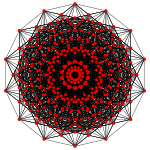
|

|
| Dihedral symmetry | [8] | [[7]] | [6] |
| Ak Coxeter plane | A4 | A3 | A2 |
| Graph | 
|

|

|
| Dihedral symmetry | [[5]] | [4] | [[3]] |
Steritruncated 7-simplex
[edit]| steritruncated 7-simplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t0,1,4{3,3,3,3,3,3} |
| Coxeter-Dynkin diagrams | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 7280 |
| Vertices | 1120 |
| Vertex figure | |
| Coxeter group | A7, [36], order 40320 |
| Properties | convex |
Alternate names
[edit]- Cellitruncated octaexon (acronym: cato) (Jonathan Bowers)[3]
Coordinates
[edit]The vertices of the steritruncated 7-simplex can be most simply positioned in 8-space as permutations of (0,0,0,1,1,1,2,3). This construction is based on facets of the steritruncated 8-orthoplex.
Images
[edit]| Ak Coxeter plane | A7 | A6 | A5 |
|---|---|---|---|
| Graph | 
|

|

|
| Dihedral symmetry | [8] | [7] | [6] |
| Ak Coxeter plane | A4 | A3 | A2 |
| Graph | 
|

|

|
| Dihedral symmetry | [5] | [4] | [3] |
Bisteritruncated 7-simplex
[edit]| bisteritruncated 7-simplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t1,2,5{3,3,3,3,3,3} |
| Coxeter-Dynkin diagrams | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 9240 |
| Vertices | 1680 |
| Vertex figure | |
| Coxeter group | A7, [36], order 40320 |
| Properties | convex |
Alternate names
[edit]- Bicellitruncated octaexon (acronym: bacto) (Jonathan Bowers)[4]
Coordinates
[edit]The vertices of the bisteritruncated 7-simplex can be most simply positioned in 8-space as permutations of (0,0,1,1,1,2,3,3). This construction is based on facets of the bisteritruncated 8-orthoplex.
Images
[edit]| Ak Coxeter plane | A7 | A6 | A5 |
|---|---|---|---|
| Graph | 
|

|
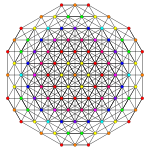
|
| Dihedral symmetry | [8] | [7] | [6] |
| Ak Coxeter plane | A4 | A3 | A2 |
| Graph | 
|

|

|
| Dihedral symmetry | [5] | [4] | [3] |
Stericantellated 7-simplex
[edit]| Stericantellated 7-simplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t0,2,4{3,3,3,3,3,3} |
| Coxeter-Dynkin diagrams | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 10080 |
| Vertices | 1680 |
| Vertex figure | |
| Coxeter group | A7, [36], order 40320 |
| Properties | convex |
Alternate names
[edit]- Cellirhombated octaexon (acronym: caro) (Jonathan Bowers)[5]
Coordinates
[edit]The vertices of the stericantellated 7-simplex can be most simply positioned in 8-space as permutations of (0,0,0,1,1,2,2,3). This construction is based on facets of the stericantellated 8-orthoplex.
Images
[edit]| Ak Coxeter plane | A7 | A6 | A5 |
|---|---|---|---|
| Graph | 
|

|

|
| Dihedral symmetry | [8] | [7] | [6] |
| Ak Coxeter plane | A4 | A3 | A2 |
| Graph | 
|

|

|
| Dihedral symmetry | [5] | [4] | [3] |
Bistericantellated 7-simplex
[edit]| Bistericantellated 7-simplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t1,3,5{3,3,3,3,3,3} |
| Coxeter-Dynkin diagrams | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 15120 |
| Vertices | 2520 |
| Vertex figure | |
| Coxeter group | A7×2, [[36]], order 80320 |
| Properties | convex |
Alternate names
[edit]- Bicellirhombihexadecaexon (acronym: bacroh) (Jonathan Bowers)[6]
Coordinates
[edit]The vertices of the bistericantellated 7-simplex can be most simply positioned in 8-space as permutations of (0,0,1,1,2,2,3,3). This construction is based on facets of the stericantellated 8-orthoplex.
Images
[edit]| Ak Coxeter plane | A7 | A6 | A5 |
|---|---|---|---|
| Graph | 
|

|

|
| Dihedral symmetry | [8] | [7] | [6] |
| Ak Coxeter plane | A4 | A3 | A2 |
| Graph | 
|

|

|
| Dihedral symmetry | [5] | [4] | [3] |
Stericantitruncated 7-simplex
[edit]| stericantitruncated 7-simplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t0,1,2,4{3,3,3,3,3,3} |
| Coxeter-Dynkin diagrams | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 16800 |
| Vertices | 3360 |
| Vertex figure | |
| Coxeter group | A7, [36], order 40320 |
| Properties | convex |
Alternate names
[edit]- Celligreatorhombated octaexon (acronym: cagro) (Jonathan Bowers)[7]
Coordinates
[edit]The vertices of the stericantitruncated 7-simplex can be most simply positioned in 8-space as permutations of (0,0,0,1,1,2,3,4). This construction is based on facets of the stericantitruncated 8-orthoplex.
Images
[edit]| Ak Coxeter plane | A7 | A6 | A5 |
|---|---|---|---|
| Graph | 
|

|

|
| Dihedral symmetry | [8] | [7] | [6] |
| Ak Coxeter plane | A4 | A3 | A2 |
| Graph | 
|

|

|
| Dihedral symmetry | [5] | [4] | [3] |
Bistericantitruncated 7-simplex
[edit]| bistericantitruncated 7-simplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t1,2,3,5{3,3,3,3,3,3} |
| Coxeter-Dynkin diagrams | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 22680 |
| Vertices | 5040 |
| Vertex figure | |
| Coxeter group | A7, [36], order 40320 |
| Properties | convex |
Alternate names
[edit]- Bicelligreatorhombated octaexon (acronym: bacogro) (Jonathan Bowers)[8]
Coordinates
[edit]The vertices of the bistericantitruncated 7-simplex can be most simply positioned in 8-space as permutations of (0,0,1,1,2,3,4,4). This construction is based on facets of the bistericantitruncated 8-orthoplex.
Images
[edit]| Ak Coxeter plane | A7 | A6 | A5 |
|---|---|---|---|
| Graph | 
|

|

|
| Dihedral symmetry | [8] | [7] | [6] |
| Ak Coxeter plane | A4 | A3 | A2 |
| Graph | 
|

|

|
| Dihedral symmetry | [5] | [4] | [3] |
Steriruncinated 7-simplex
[edit]| Steriruncinated 7-simplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t0,3,4{3,3,3,3,3,3} |
| Coxeter-Dynkin diagrams | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 5040 |
| Vertices | 1120 |
| Vertex figure | |
| Coxeter group | A7, [36], order 40320 |
| Properties | convex |
Alternate names
[edit]- Celliprismated octaexon (acronym: cepo) (Jonathan Bowers)[9]
Coordinates
[edit]The vertices of the steriruncinated 7-simplex can be most simply positioned in 8-space as permutations of (0,0,0,1,2,2,2,3). This construction is based on facets of the steriruncinated 8-orthoplex.
Images
[edit]| Ak Coxeter plane | A7 | A6 | A5 |
|---|---|---|---|
| Graph | 
|

|

|
| Dihedral symmetry | [8] | [7] | [6] |
| Ak Coxeter plane | A4 | A3 | A2 |
| Graph | 
|

|

|
| Dihedral symmetry | [5] | [4] | [3] |
Steriruncitruncated 7-simplex
[edit]| steriruncitruncated 7-simplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t0,1,3,4{3,3,3,3,3,3} |
| Coxeter-Dynkin diagrams | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 13440 |
| Vertices | 3360 |
| Vertex figure | |
| Coxeter group | A7, [36], order 40320 |
| Properties | convex |
Alternate names
[edit]- Celliprismatotruncated octaexon (acronym: capto) (Jonathan Bowers)[10]
Coordinates
[edit]The vertices of the steriruncitruncated 7-simplex can be most simply positioned in 8-space as permutations of (0,0,0,1,2,2,3,4). This construction is based on facets of the steriruncitruncated 8-orthoplex.
Images
[edit]| Ak Coxeter plane | A7 | A6 | A5 |
|---|---|---|---|
| Graph | 
|

|

|
| Dihedral symmetry | [8] | [7] | [6] |
| Ak Coxeter plane | A4 | A3 | A2 |
| Graph | 
|

|

|
| Dihedral symmetry | [5] | [4] | [3] |
Steriruncicantellated 7-simplex
[edit]| steriruncicantellated 7-simplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t0,2,3,4{3,3,3,3,3,3} |
| Coxeter-Dynkin diagrams | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 13440 |
| Vertices | 3360 |
| Vertex figure | |
| Coxeter group | A7, [36], order 40320 |
| Properties | convex |
Alternate names
[edit]- Celliprismatorhombated octaexon (acronym: capro) (Jonathan Bowers)[11]
Coordinates
[edit]The vertices of the steriruncicantellated 7-simplex can be most simply positioned in 8-space as permutations of (0,0,0,1,2,3,3,4). This construction is based on facets of the steriruncicantellated 8-orthoplex.
Images
[edit]| Ak Coxeter plane | A7 | A6 | A5 |
|---|---|---|---|
| Graph | 
|

|

|
| Dihedral symmetry | [8] | [7] | [6] |
| Ak Coxeter plane | A4 | A3 | A2 |
| Graph | 
|

|

|
| Dihedral symmetry | [5] | [4] | [3] |
Bisteriruncitruncated 7-simplex
[edit]| bisteriruncitruncated 7-simplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t1,2,4,5{3,3,3,3,3,3} |
| Coxeter-Dynkin diagrams | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 20160 |
| Vertices | 5040 |
| Vertex figure | |
| Coxeter group | A7×2, [[36]], order 80320 |
| Properties | convex |
Alternate names
[edit]- Bicelliprismatotruncated hexadecaexon (acronym: bicpath) (Jonathan Bowers)[12]
Coordinates
[edit]The vertices of the bisteriruncitruncated 7-simplex can be most simply positioned in 8-space as permutations of (0,0,1,2,2,3,4,4). This construction is based on facets of the bisteriruncitruncated 8-orthoplex.
Images
[edit]| Ak Coxeter plane | A7 | A6 | A5 |
|---|---|---|---|
| Graph | 
|

|

|
| Dihedral symmetry | [8] | [[7]] | [6] |
| Ak Coxeter plane | A4 | A3 | A2 |
| Graph | 
|

|

|
| Dihedral symmetry | [[5]] | [4] | [[3]] |
Steriruncicantitruncated 7-simplex
[edit]| steriruncicantitruncated 7-simplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t0,1,2,3,4{3,3,3,3,3,3} |
| Coxeter-Dynkin diagrams | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 23520 |
| Vertices | 6720 |
| Vertex figure | |
| Coxeter group | A7, [36], order 40320 |
| Properties | convex |
Alternate names
[edit]- Great cellated octaexon (acronym: gecco) (Jonathan Bowers)[13]
Coordinates
[edit]The vertices of the steriruncicantitruncated 7-simplex can be most simply positioned in 8-space as permutations of (0,0,0,1,2,3,4,5). This construction is based on facets of the steriruncicantitruncated 8-orthoplex.
Images
[edit]| Ak Coxeter plane | A7 | A6 | A5 |
|---|---|---|---|
| Graph | 
|

|

|
| Dihedral symmetry | [8] | [7] | [6] |
| Ak Coxeter plane | A4 | A3 | A2 |
| Graph | 
|

|

|
| Dihedral symmetry | [5] | [4] | [3] |
Bisteriruncicantitruncated 7-simplex
[edit]| bisteriruncicantitruncated 7-simplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t1,2,3,4,5{3,3,3,3,3,3} |
| Coxeter-Dynkin diagrams | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 35280 |
| Vertices | 10080 |
| Vertex figure | |
| Coxeter group | A7×2, [[36]], order 80320 |
| Properties | convex |
Alternate names
[edit]- Great bicellated hexadecaexon (gabach) (Jonathan Bowers) [14]
Coordinates
[edit]The vertices of the bisteriruncicantitruncated 7-simplex can be most simply positioned in 8-space as permutations of (0,0,1,2,3,4,5,5). This construction is based on facets of the bisteriruncicantitruncated 8-orthoplex.
Images
[edit]| Ak Coxeter plane | A7 | A6 | A5 |
|---|---|---|---|
| Graph | 
|

|

|
| Dihedral symmetry | [8] | [[7]] | [6] |
| Ak Coxeter plane | A4 | A3 | A2 |
| Graph | 
|

|

|
| Dihedral symmetry | [[5]] | [4] | [[3]] |
Related polytopes
[edit]This polytope is one of 71 uniform 7-polytopes with A7 symmetry.
Notes
[edit]- ^ Klitizing, (x3o3o3o3x3o3o - sco)
- ^ Klitizing, (o3x3o3o3o3x3o - sabach)
- ^ Klitizing, (x3x3o3o3x3o3o - cato)
- ^ Klitizing, (o3x3x3o3o3x3o - bacto)
- ^ Klitizing, (x3o3x3o3x3o3o - caro)
- ^ Klitizing, (o3x3o3x3o3x3o - bacroh)
- ^ Klitizing, (x3x3x3o3x3o3o - cagro)
- ^ Klitizing, (o3x3x3x3o3x3o - bacogro)
- ^ Klitizing, (x3o3o3x3x3o3o - cepo)
- ^ Klitizing, (x3x3x3o3x3o3o - capto)
- ^ Klitizing, (x3o3x3x3x3o3o - capro)
- ^ Klitizing, (o3x3x3o3x3x3o - bicpath)
- ^ Klitizing, (x3x3x3x3x3o3o - gecco)
- ^ Klitizing, (o3x3x3x3x3x3o - gabach)
References
[edit]- H.S.M. Coxeter:
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380–407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D.
- Klitzing, Richard. "7D uniform polytopes (polyexa)". x3o3o3o3x3o3o - sco, o3x3o3o3o3x3o - sabach, x3x3o3o3x3o3o - cato, o3x3x3o3o3x3o - bacto, x3o3x3o3x3o3o - caro, o3x3o3x3o3x3o - bacroh, x3x3x3o3x3o3o - cagro, o3x3x3x3o3x3o - bacogro, x3o3o3x3x3o3o - cepo, x3x3x3o3x3o3o - capto, x3o3x3x3x3o3o - capro, o3x3x3o3x3x3o - bicpath, x3x3x3x3x3o3o - gecco, o3x3x3x3x3x3o - gabach







































































