Talk:Adiabatic process
| This It is of interest to the following WikiProjects: | |||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||
Accuracy Dispute & Changes, 2008-03-26[edit]
I made several changes to the article, and more may be needed. In order of appearance on the page:
1) Paragraph 3 previously stated:
"...A transformation of a thermodynamic system can be considered adiabatic when it is quick enough that no significant heat is transferred between the system and the outside. The adiabatic process can also be called quasi-static..."
The second sentence is confusing or simply incorrect; a quasi-static process is one in which all states can effectively be considered equilibrium states (see quasi-static), which seems to apply better to a case when the gas does come into thermal equilibrium with the outside of the system. Although a quasi-static assumption may be necessary for a reversible process (don't know this for sure), it is certainly not necessary for an adiabatic process (e.g., a rapid, irreversible gas expansion where inertial effects are important). I have removed it to avoid confusion.
2a) In the "Adiabatic Heating and Cooling" section, Paragraph 2 previously stated:
Adiabatic cooling occurs when the pressure of a substance is decreased, such as when it expands into a larger volume. An example of this is when the air is released from a pneumatic tire; the outlet air will be noticeably cooler than the tire.
The phrase "such as when it expands into a larger volume" suggests a gas flowing into a larger volume or reservoir, which is incorrect. The spirit of the sentence is that gas increasing in volume undergoes adiabatic cooling, but this is ambigious in the original wording. I have replaced it with "...the pressure of a substance is decreased as it does work on its surroundings," which is closer to the reality. However, this still doesn't mention a volume increase, which would be nice to have (i.e., an explanation of the fact that a gas increasing in volume and thus decreasing in pressure--or vice versa--does work on its environment, and thus cools).
You failed to note refrigeration and industrial air compression.
Heat becomes a real problem in pneumatic systems, requiring intercoolers on two and three stage machines over about 10 HP. It would be simpler and clearer to note that all gasses (except Bose Einstein condensates at 0 K) contain heat. Compressing the gas increases the temperature. Draw off air and the tank -- and the tool -- both cool down considerably.
You also failed to note precipitation. ALL adiabatic (as compared to isothermal) compressor systems precipitate water, dust, CO, CO2, and other materials from atmospheric air. Linde's Principle states that gas will not liquefy until it reaches the Linde Limit. Pressurize air sufficiently, cool the compressed gasses enough, and the gasses will condense to liquids, one at a time. Pardon me if I defer to release proprietary information.
The primary use for adiabatic technology is refrigeration. Condenser units pressurize refrigerant, run air (or with chilled water systems, water) over the coils, pulling heat from the refrigerated space. Reverse the process (by valving) and we suddenly have the normal home heat pump. —Preceding unsigned comment added by 209.244.31.59 (talk) 20:24, 17 April 2008 (UTC)
2b) I removed the example of air being released from a pneumatic tire in the quote above, as the cooling is partially due to the Joule-Thomson effect, not entirely due to adiabatic expansion. Some cooling due to adiabatic expansion may be observed inside the tire itself (the volume of gas which remains in the tire at any given time is expanding and doing work on the exiting air), but this does not account for the reason air may feel cold as it just begins to exit the tire. Adiabatic expansion may be noticeable as a decrease in the temperature of the tire though how much so depends on the heat capacity and mass of the rubber relative to those of the gas.
A good analogy here is an aerosol can. The can cools in your hand as it is sprayed due to evaporation of the fluid inside (similar to adiabatic expansion), and the stream coming out of the nozzle is cooled by some combination of adiabatic expansion and the Joule-Thomson effect.
It would be nice if someone could find a good "everyday life" example for this section that does not include a dissipative/irreversible process, though... the best I can think of right now is a vacuum pump (when gas is expanded by a piston inside a cylinder), but I don't think many people will be able to relate to this, and it's not immediately apparent that the gas does net work on the piston as is required for adiabatic cooling (it seems to be the other way around at first glance). Perhaps a pneumatic piston motor would work well, where expanding high-pressure gas does work on a piston, and should come out colder than it went in?
3) In the "Ideal Gas" section, Paragraph 1 previously stated:
"The mathematical equation for an ideal fluid undergoing an adiabatic process is"
This entire section is only valid for a reversible (isentropic) process, and does not apply to, say, a mass passing through a throttle (even though this is an adiabatic process). I've updated the section heading, introductory sentence, and the beginning of the second paragraph ("For adiabatic processes, it is also true that") to reflect this. However, more changes may be needed throughout the section, and it would be nice to have an explanation of why this applies only in the reversible case... in short, it's because the work on a gas volume does not equal PdV any more, but some things may be said about inertial or viscous effects, quasi-statics (relating to pressure changes and reversibility, not thermal interactions with the system boundary), etc.
Thanks in advance for any contributions to the article!
Cheers, --Masegado (talk) 20:53, 26 March 2008 (UTC)
Continental and local scale[edit]
can you help me with a continental or global scal in the atmosphere and a local or regional scale
Continental or Global scale would be the Hadley cell and a local or regional scale would be sea and land breezes.
Hope this helps!
Perhaps articles like Joule-Thomson effect should be considered as relevant to the topic. --Saperaud 08:04, 22 December 2005 (UTC)
Edit, 2006/01/30[edit]
I edited the section on adiabatic heating/cooling. The "coolness" felt when pursing one's lips and blowing on one's own skin is due almost entirely to enhanced convective heat transfer; the actual air temperature drop is so small (due to the tiny pressure drop involved) that if one blows on a thermometer in this manner, there will be a negligible temperature change.
I instead offered the different example of deflating a tire, where the pressure drop is on the order of several hundred KPa (several dosen psi); I have seen frost form on valve stems because of this.
Also added the more extreme heating example of a motorized air compressor operating at higher pressures than a bicycle pump.
Joe Frickin Friday 17:54, 30 January 2006 (UTC)
Very similar effect occurs when looking at a Methonol Cannon, you can observe this phenomenon very easily
added 2006-01-04[edit]
in 'Derivation of formula' section equation (3) there is dE = something - shouldn't it be dU ?
Symbol for the ratio of specific heats[edit]
I fully realize that the Greek letter gamma () is used by physicists and others as the symbol representing the ratio of specific heat at constant pressure to the specific heat at constant volume. However, I would like to point out that thousands of engineers worldwide use a lowercase k to represent that ratio. I strongly believe that this article should mention that fact. mbeychok 00:10, 1 March 2006 (UTC)
Adiabat?[edit]
So, what exactly is an adiabat shit? The article doesn't make this clear. Jonabbey 04:31, 7 June 2006 (UTC)
- I belive it is a line on a graph that indicates 0 heat flow along that line, like an isotherm is a line denoting constant temperature.
- Correct. An adiabat is a curve on the pV graph where Q=0. An adiabatic process is one that follows one of these curves. An adibat is always steeper than an isotherm. 75.5.254.164 00:51, 11 December 2006 (UTC)
- No, an adiabat is a curve with constant entropy (i.e. its an "isentrope"). Q (or δQ) is not a state function, so there are many curves through the same point that could be adiabatic, but only one that is isentropic. PAR 02:58, 11 December 2006 (UTC)
Derivation of TV^gamma-1[edit]
The derivation of TV^gamma-1 is a lot longer than the one in my physics text book (Young & Friedman 11th ed.) and doesn't explain what Cv is. I'd fix this myself, but my mathML sucks. 75.5.254.164 00:51, 11 December 2006 (UTC)
We are doing a project on the adiabatic process and we need a lot of help. Can anyone help us? 63.172.1.2 13:42, 28 February 2007 (UTC)Paco and Taco
Something seems wrong to me: Equation (1) states that dU = - δW, whereas first equation below equation (4) states that δW = - p dV = α p dV + α V dp = dU, i.e. δW = dU. Giving that the end of the derivation is correct, there should be a confusion between the physical definition of work (work done by the system) and the chemical one (work done on the system). Equation (1) is valid for physical work definition. Question: is equation (2) valid for physical work or chemical work ? Parey (talk) 08:07, 25 January 2008 (UTC)
Adiabatic Internal combustion Engine[edit]
Fountain Powerboats of Washington NC claims to have created an adiabatic internal combustion engine based upon a marinized Chevrolet engine. Though the project has not proven publicly it is really an adiabatic cycle engine it has demonstrated extreme power production. Anyone care to propose how this would work?
Jsmithnc 20:25, 13 August 2007 (UTC)
- Sounds exciting to buy shares, before gets noticed. 84.227.255.16 (talk) 09:05, 16 September 2014 (UTC)
Discrete Formula[edit]
It looks like something is wrong with the final form of the discrete formula derived - if you just plug in the ideal gas law for t2 and t1 and cancel things, you get alpha=-1 always. This can't be right - alpha depends on the degrees of freedom for the particular molecules (ndof/2), and could take on many values. —The preceding unsigned comment was added by 67.161.105.146 (talk) 07:15, August 21, 2007 (UTC)
No heat being transferred is necessary but not sufficient[edit]
E.g. if an isolated system undergoes a rapid change leading to entropy production, then that is not an adiabatic change. At least not in theoretical physics (I'm not sure about engineering or chemistry, they often teach physics in a flawed way) :)
In practice, it may well be the case that systems undergoing a rapid change are closer to the ideal adiabatic process than systems that change slowly, because in practice the heat transfer issue may be more important than entropy production. But one always has to explain things from the fundamentals and then explain how it is (approximately)realized in real world phenomena.
This article also fails to mention the Adiabatic theorem of quantum mechanics, which is absolutely fundamental to this topic. Count Iblis (talk) 17:58, 30 April 2008 (UTC)
plot[edit]
the P-V diagram is useless without labels. both axes and isolines should be labeled, right now it just looks like modern art. 141.211.231.47 (talk) 00:18, 8 November 2008 (UTC)
I believe that the figure is incorrect, as it shows "work done" as the region between the adiabatic expansion line and the x-axis. Work done should be the region between the adiabat line to the final state.24.121.241.18 (talk) 08:32, 17 April 2009 (UTC)
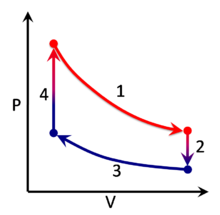
- Each thermodynamic cycle can be split into separated to multiple thermodynamic processes, with an adiabatic process being just one of several types of thermodynamic processes.siNkarma86—Expert Sectioneer of Wikipedia
86 = 19+9+14 + karma = 19+9+14 + talk 22:48, 16 September 2011 (UTC)
Adiabatic process in liquid (for instance, water)[edit]
The article describes case of ideal gas; there is no information about real gases or liquids. Consider the following problem, for instance:
Temperature of water in ocean is 12oC, and temperature coefficient of expansion is equal to 9.2*10-5 K-1. Some water moves from the surface to the bottom (1km under surface) quickly (thus, it doesn't exchange heat with other water). Find the approximate change of its temperature. Wikiwide (talk) 23:46, 13 April 2009 (UTC)
Here's the deal. I give you the solution to the problem: Here it is:
http://www.physicsforums.com/showthread.php?t=304987
(the reply by me (Count Iblis), of course :) )
Then you are going to make sure you understand it and then you are going to write a paragraph in this wiki article about this thermodynamic derivation. Count Iblis (talk) 00:13, 14 April 2009 (UTC)
Possible Plagiarism[edit]
While reading the article I've seen a few lines that look eerily familiar. At the same time some of the derivations are literally straight out of a textbook. I'll be the first to admit that a derivation is a derivation so I highly doubt that those are clear indicators, but the article really does read like it may have been copied out of one or many textbooks.
At the moment I cannot substantiate this claim, but I think it warrants some research. If in fact the article is copied word for word we should be careful not to delete the page wholesale but salvage the bits of it that are legitimate, namely the derivations and equations which, as far as I know, cannot be copy-written.
DacodaNelson (talk) 03:08, 16 April 2011 (UTC)
- "If in fact the article is copied word for word we should be careful not to delete the page wholesale but salvage the bits of it that are legitimate, namely the derivations and equations which, as far as I know, cannot be copy-written." When will the world realize that there are only so many ways to say something concisely? We will reach a point where certain small points are off-limits to a free encyclopedia simply because copy-written material has all but exhausted every way of making a point that doesn't waste the reader's time.siNkarma86—Expert Sectioneer of Wikipedia
86 = 19+9+14 + karma = 19+9+14 + talk 22:04, 16 September 2011 (UTC)
- I agree with the sentiment but I'm confident the remixers will win. Some will even go on to found billion-dollar companies. 84.227.255.16 (talk) 08:53, 16 September 2014 (UTC)
Just wrong[edit]
An adiabatic process must involve both no heat transfer with the surroundings (adiathermal) AND it must be reversible. See "Concepts in Thermal Physics" by Blundell and Blundell. — Preceding unsigned comment added by 92.21.105.198 (talk) 21:28, 4 December 2011 (UTC)
- I agree that some textbooks define it that way, but many don't. In theoretical physics, one would rather not define adiabatic to be also (potentially) an irreversible process (because that would bring it in conflict with another notion of "adiabatic" used in physics). But in engineering it is common to use "adiabatic" also for irreversible processes. I think in the book by Reif a comment is made about this, and Reif prefers not to use the word "adiabatic" at all to avoid confusion. Count Iblis (talk) 22:29, 4 December 2011 (UTC)
Relation to adiabatic theorem[edit]
Could someone explain the relation to adiabatic theorem. One says that family of differential equations $L(x',x,t,p)=0$ parametrized by parameter $p$ satisfies adiabatic theorem, if denoting solutions of $L(x',x,t,p)=0$ by $x(t,p)$, one has $x(t,p(t))$ are close to the solutions of $L(x',x,t,p(t))=0$, if dependence of $p(t)$ is "slow" (derivative is small). I know, that Hamiltonian dynamics satisfies adiabatic theorem, but relation to heat transfer eludes me. Slava Matveev. 194.94.96.194 (talk) 14:00, 10 December 2012 (UTC)
When is adiabatic not adiabatic?[edit]
.... when it's contained in this article.
- Adiabatic heating also occurs in the Earth's atmosphere when an air mass descends, for example, in a katabatic wind or Foehn or chinook wind flowing downhill over a mountain range. When a parcel of air descends, the pressure on the parcel increases. Due to this increase in pressure, the parcel's volume decreases and its temperature increases, thus increasing the internal energy.
If the internal energy (which can only be kinetic, i.e. heat) increases the process cannot be adiabatic. Increasing pressure doesn't affect the kinetic energy of the molecules. That violates the first law of thermodynamics. This article is as muddled as Lapse rate is as far as the description of adiabatic processes goes. Rambler24 (talk) 23:02, 2 March 2013 (UTC)
- Increasing the pressure DOES increase the kinetic energy of the molecules. Compressing a given amount of gas adiabatically increases its temperature. For a fixed amount of gas undergoing a reversible (i.e. slow) process, and for an adiabatic process, so that . You do work on a gas and subtract none by thermal means, its internal energy increases. Increasing the pressure by compression increases the kinetic energy of the particles. Intuitively, if you have piston that is compressing the gas, the particles are bouncing off the piston wall, which is moving towards them, so their energy after the collision is increased. If the process is done very slowly, then yes, the amount of energy added per collision becomes very small, but it takes a longer time, (so more collisions) to accomplish a given volume decrease. So the product of the two stays the same, its the amount of work done during that volume decrease, and that's the increase in internal energy (i.e. kinetic energy of the particles). PAR (talk) 05:38, 3 March 2013 (UTC)
Here are 2 flaws in the article's wording and why PAR's response doesn't answer Rambler's objection: 1) "Adiabatic heating occurs when the pressure of a gas is increased from work DONE ON IT by its surroundings, e.g. a piston compressing a gas contained within an adiabatic cylinder." If this process is adiabatic, the compression occurs without hitting any of the gas in the cylinder. The gas is the system, the piston is part of the environment, and you only move the piston when there's a thin disk of evacuated volume next to the piston. The gas's pressure increases not because its molecules are sped up, but because they are confined to less volume. The article's wording implies to some readers that the gas itself is being moved by the compression, but it's the gas's BOUNDARIES that are moved. We don't have to fudge anything or bring up differentials and round them to 0.
2) The part that says "the parcel's volume decreases and its temperature increases, thus increasing the internal energy" and the part below that says "as the volume increases, the temperature falls and internal energy decreases" are technically correct for the real gases described, but they imply that the internal energy change is a result of the adiabatic change in system volume. The change in internal energy happens only due to the interactions that AREN'T adiabatic, the ones that we fudge over to call the process adiabatic. A change in internal energy directly contradicts the process being adiabatic. An ideal gas in the pure adiabatic process would have no change in internal energy. 173.25.54.191 (talk) 23:38, 27 March 2013 (UTC)
- Rambler24 has written If the internal energy increases the process cannot be adiabatic. I ask that he explain where that comes from, or why he believes it to be correct.
- I believe it to be incorrect. I can offer the following explanation of my belief. Imagine a gas in an insulated cylinder, underneath a movable piston. Mechanical work is done on the piston in order to reduce the volume of the gas and increase its pressure and temperature. Unless heat begins to flow into the walls of the cylinder and piston, no transfer of heat occurs so the process is adiabatic (and reversible). However, the temperature of the gas has increased significantly so its internal energy has increased too. In fact, the increase in internal energy exactly matches the mechanical work done on the gas (and on the piston). Dolphin (t) 23:54, 27 March 2013 (UTC)
Dolphin, an increase in temperature doesn't have to equal an increase in internal energy. You can add heat to a system, increasing its internal energy, without changing its temperature, if it's allowed to expand. Likewise, you can increase a system's temperature by adiabatically compressing it (imagine a really diffuse gas that would be easier to compress without hitting the gas), without adding any internal energy to the gas's molecules. A volume's temperature is a function of not just average kinetic energies of its molecules, but also of the total number of molecules and the total volume. Adding heat to a system by definition increases its internal energy. 173.25.54.191 (talk) 00:14, 28 March 2013 (UTC)
- I"m afraid that the article as it stands, as well as PAR and Dolphin51 are all quite correct. "Adiabatic" means that no heat is being transfered in or out of a sytsem, not that no work is being done on or by the system. In an adiabatic process, the system is quite free to do work, or have work done upon it. It's simply insulated from HEAT transfers, but NOT from "heating up" or "cooling off" (changing temperature). It is only forbidden to change temp as a result of HEAT going in or out directly. Temperature of the system can go up, down, or stay constant. The same is true of the internal energy of the system, which now is simply driven by the PV work done by (or to) the sytsem.
I do not know where Ramber24 and the IP (perhaps they are the same?) got the odd idea that "adiabatic" had something to do with no PV work.
Finally, I don't know how we started to treat the odd idea of a "Maxwell's demonic" spontaneous compression, where we confine a gas to a smaller volume merely by waiting until it exerts no piston pressure, then quickly move the piston in, so we get the compression free with no PV work. You can let a gas expand that way, and an ideal gas indeed does not change temperature. But you can't compress a gas that way unless you're Maxwell's demon. Good luck with that, as you'd be able to do all kinds of entropy-decreasing things. In the real world, the problem of figuring out where the gas molecules are located, so you can figure out when to move the piston without moving it against the force of impacts (thus doing PV work), would defeat you. BTW, even if you managed this (defeating the second law) the first law would ensure that you got nothing directly for it, and the gas temperature (ideal gas) would no more change in such a "spontaneous contraction" than it does in a sponteous isothermal expansion. After all, where would the energy come from, to change the temperature of the gas? You did no work on it. You didn't heat it. Its internal energy must therefore stay the same as always. SBHarris 02:40, 28 March 2013 (UTC)
We got the maxwell's demon part from me not understanding that even though I would say in conversation that compressing a gas 'heats' it, that is formally wrong. Not realizing that, then to make sense of adiabatic processes involving no heat transfer, I had to imagine a way to increase the system's pressure without giving it any energy. On top of that I thought the temperature would go up in a volume if its molecules maintained their energies but were concentrated into a smaller volume, using the colloquial notion that my cozy room would feel colder if the air was rarer but the molecules still had the same average kinetic energy. Bam, there you have it. I cringe at how epically wrong I was on this page and am glad to be corrected. 173.25.54.191 (talk) 04:27, 28 March 2013 (UTC)
Needs a correction....[edit]
Three-fourths down this thread it is stated "Substituting γ=(α+2)/α" that seems incorrect. Should it not be "Substituting γ=(α+1)/α" ? If so, the following derivation may need updating. — Preceding unsigned comment added by 76.242.181.95 (talk) 17:01, 12 May 2013 (UTC)
Variable of differentiation[edit]
Pondhockey (talk) 04:14, 18 April 2014 (UTC) It seems to be a tradition within thermodynamics to omit the variable of differentiation (differentiation with respect to what?) A link to an explanation would be very helpful to outsiders (such as myself) who have no clue what dU = ... even means.
- You can understand it by assuming all the quantities are functions of t and dividing all the differentials by dt.
- An alternate way to understand it is by realizing that dU, dp, dV, dS and dT are differential 1-forms. (The article is not much fun for beginners, but it is the true answer.) They are defined on a 2-dimensional submanifold M of R5 (with coordinates U, p, V, S, T), where M is defined by the equations U=U(V,S), p=-(∂U/∂V)(V,S), T=(∂U/∂S)(V,S). But actually any two of the 5 variables can be taken as independent coordinates. The equation S=S(U,V) is probably more natural and fundamental. See Sackur-Tetrode equation for the case of a monatomic ideal gas (treat m and N as constants.).
- An equation such as dU = p dV - S dT can be understood as an equation for 1-forms on M. Or it can be understood by dividing by dt, as mentioned in the first paragraph. Then you get dU/dt = p(t)dV/dt - S(t)dT/dt
- Heat and work, Q and W, can be understood as functions of t, but not as functions on the manifold M. (They are not state functions.) We may assign Q(0) and W(0) arbitrarily, and then Q(t) and W(t) are the amount of heat and work that flow into the body between time t=0 and time t. They satisfy dU/dt = dQ/dt + dW/dt and dS/dt ≥ (1/T(t))dQ/dt.
178.38.77.196 (talk) 23:13, 13 March 2015 (UTC)
Adiabatic vs adiathermal[edit]
Is this process adiabatic or adiathermal? Which term is more suited?--188.26.22.131 (talk) 10:33, 19 May 2014 (UTC)
- The two terms describe very different and mutually exclusive systems. Which term is more suited depends on what kind of system is being described. VQuakr (talk) 18:11, 10 June 2014 (UTC)
- With respect, I think an adiathermal wall is just the same thing as an adiabatic wall, at least in macroscopic thermodynamics. They both pass energy as work but not as heat, and do not pass matter.
- I would be interested in VQuakr's reasons for his apparently differing view when talking of a process as distinct from a wall. Perhaps he is thinking of the near inversion of meaning that is described in the article in the section Usage of the word adiabatic, referring to a special usage in quantum statistical mechanics?
- By my observation, the term adiabatic is much more common in physics today that the term adiathermal. In the nineteenth century adiathermal was very often used to describe a wall, but very rarely so today. I do not recall talk of adiathermal processes.Chjoaygame (talk) 23:26, 10 June 2014 (UTC)
Equation derivation[edit]
How is the equation of the adiabatic pV^gamma derived? From what starting point? Is it necessary to involve Mayer's relation in the derivation?--188.26.22.131 (talk) 12:58, 11 July 2014 (UTC)
question about "derivative"[edit]
Can someone note what the derivative, in equation 3, is with respect to? — Preceding unsigned comment added by Pondhockey (talk • contribs) 21:37, 14 August 2014 (UTC)
- It is customary to start a new section at the bottom of the page, as here, for a question like this. If the first character in a line of edit is a blank, then the line is put into a box.
- As it happens, the question is not clearly asked. It would need to be made more precise to get an answer.Chjoaygame (talk) 06:15, 15 August 2014 (UTC)
- I think you mean the derivative that occurs between eqn (3) and eqn (4).
- It is an differential, the d operator, a so-called "exterior derivative". The result has the same general content as a gradient (in this context, where d is applied to a scalar), but it is formally defined as a point-dependent covector (i.e. a 1-form). See differential form, but you only need the 1-forms. Differential forms give a rigorous and precise meaning to such terms as dU, dV, etc -- they are not infinitesimals (motivational fictions) but linear transformation and functions (real objects).
- To answer your original question: the derivative is not taken with respect to any one numerical variable, but with respect to a variable point in the state space, which in this case is 2-dimensional, and can be parametrized by (P,V) but also by (P,T), (V,T), or other pairs acting as the independent variables. dU, dV, dP, etc all make sense here (in fact df for any function) and have the relationship specified in (4). 84.227.255.16 (talk) 08:48, 16 September 2014 (UTC)
The current discussion of the adiabatic theorem is quite confusing.[edit]
The current discussion of the adiabatic theorem is quite confusing. It focusses on a specific consequence of adiabaticity rather than on the differences in the definition. In quantum theory adiabatic means that the quantum number of one degree of freedom (usually the electronic state) does not change as the another degree of freedom is changed (usually the nuclear positions.) The current discussion of a compression is not really a useful comparison as it requires invocation of the interactions of unbound particles, which is not the context in which the concept of adiabaticty is usually considered. A better connection between the use of adiabatic between the two fields would be to look at the flow of energy. In essence the adiabatic concept in quantum theory tells us that energy does not flow from one type of degree of freedom to another. So nuclear motion is decoupled from electronic motion. Looking at the definition of adiabatic rather than at the consequences of adiabaticity makes the relationship much more clear. I don't have time to change the discussion, but I wish someone would as it is confusing, misleading, and misrepresentative of adiabaticity in quantum theory. 130.68.23.205 (talk) 16:04, 24 October 2014 (UTC)
- As you may see, I have moved the above comment to the bottom of the page as is customary here. The writer of the above comment is evidently an expert in quantum theory. He tells us that he doesn't have time to change the article. It would be more comfortable if he would very kindly think up a suitable user name and register it and use it instead of just an IP address.
- The term adiabatic originated in the mid-nineteenth century in classical thermodynamics where its meaning is clear and simple. For lack of vocabulary inventiveness, quantum theorists have appropriated the word to refer to a particular kind of perturbation of a system treated quantum mechanically. The appropriated meaning is loosely and slipperily derivable from the original meaning, but in some respects seems almost opposite to it.
- The original meaning in classical thermodynamics does not consider particles, either implicitly or explicitly, but the quantum mechanical meaning is essentially to do with particles.
- There are two articles, Adiabatic theorem, for quantum theorists, and Adiabatic process, for thermodynamicists, in which the words are used radically differently. The present article 'Adiabatic process' explicitly points out that there are two meanings, depending on context. The article 'Adiabatic theorem' assumes that the original meaning has been entirely obliterated and should not be mentioned.
- The above comment is concerned that the example of the present article to show the difference in meaning is unsuitable to make clear what the above comment regards as the usual meaning in quantum theory. That is probably so, but at least it does make some slight sense for quantum theory. A problem is that the example he refers to in quantum theory could not make sense at all for the thermodynamic meaning.Chjoaygame (talk) 17:48, 24 October 2014 (UTC)Chjoaygame (talk) 20:12, 24 October 2014 (UTC)
- Chjoaygame, am I correct in interpreting your comments as being opposed to additional examples because they do not sufficiently tie in to the original thermodynamic definition of the term to be included in this particular article? Would you (and other editors) be alright if I included a link to the Adiabatic theorem page from within this section so that readers at least have more direct access to such quantum-specific examples without having to redundantly include them here? JCMPC (talk) 14:59, 16 September 2016 (UTC)
- Thank you for this. I have made an edit which may do the job?Chjoaygame (talk) 05:06, 17 September 2016 (UTC)
- Pointing the interested reader from this article to the quantum article is an excellent idea. However I have replaced the mention at the end of the lead by a hatnote at the beginning of the article, so that a reader who is interested in the quantum term will be redirected immediately.
- And I have also added a similar hatnote to the article Adiabatic theorem pointing to this article, so that a reader of that article who is interested in the thermodynamic term will also be redirected immediately. Dirac66 (talk) 22:49, 30 October 2016 (UTC)
latest edit by User:Zedshort[edit]
Editor Zedshort's latest edit to this article on the adiabatic process contains errors in physics. He is making it up off the top of his head as he goes along. Still, I think it can often be better not to reward such editing by trying repeatedly to revise it.Chjoaygame (talk) 22:06, 3 November 2014 (UTC)
Editor Zedshort continues his activity. He is not citing reliable sources; indeed he is not citing any sources. Rather, he is continuing to make it up off the top of his head. Moreover, he has not corrected his errors of physics. Still perhaps better not to reward him by revising his edits? Chjoaygame (talk) 04:18, 5 November 2014 (UTC)
Characterization of isochoric[edit]
The other extreme kind of work is isochoric work (dV = 0), for which energy is added as work solely through friction or viscous dissipation within the system.
In the isochoric case, couldn't there be other entropy-producing mechanisms, such as electrical resistance, etc. ? Also, the phrasing gives the impression that "isochoric" requires entropy production. Actually, you could do nothing at all, and it would still be isochoric.
The other extreme kind of work in an adiabatic process is work that flows only into entropy production (through friction or viscous dissipation, etc) but leaves the volume unchanged (an isochoric process).
Besides leaving the list of mechanisms open, this puts the emphasis on the entropy production and fixed volume rather than the terminology.
I also noticed this sentence:
Hence, the expression "isochoric work", is used to describe irreversible work.
Again, this gives the impression that isochoric is a synonym for irreversible, or that an irreversible process is necessarily isochoric. If this is the case, then the article isochoric is misleading: there it states that isochoric means there is no change in volume.
Or perhaps the total work input breaks up into "reversible" and "irreversible" parts, the latter also being called "isochoric work"? I saw this in Kittel and Kroemer. This actually makes sense. Of course the descriptors don't attach to individual energy blobs, but as a summary number about the part of the work you can recover when you move the state variables reversibly back to their original positions, it's well-defined. Does the given citation support this?
If this is the case, how about:
Hence, the expression "isochoric work", is used to describe the portion of the work done on the system that cannot be recovered ("irreversible work"), even in situations where dV≠0 (the process is not "isochoric" in the sense of unchanging volume.
Or another alternative:
Any work done on the system during an adiabatic, isochoric process is unrecoverable, as there are no places left (meaning system variables besides entropy and temperature) where the work energy can go to be stored.
But this is shorter:
Hence, the expression "isochoric work", has come to be used to describe the portion of the total work that is lost as "irreversible work".
89.217.4.12 (talk) 12:17, 14 March 2015 (UTC)
Role of supercharger?[edit]
This is why a high compression engine requires fuels specially formulated to not self-ignite (which would cause engine knocking when operated under these conditions of temperature and pressure), or that a supercharger and intercooler to provide a lower temperature at the same pressure would be advantageous.
Does a supercharger really achieve lower temperature at the same pressure? Isn't it just higher pressure at a given (or higher) temperature?
I would think that the cooling is the crucial point. But maybe a supercharger does more than just provide extra compression?
89.217.4.12 (talk) 16:25, 14 March 2015 (UTC)
- I agree that the inter-cooling is the source of the advantage where a lower temperature is concerned. A single-stage supercharger is beneficial because it raises the volumetric efficiency of the engine, but the rise in temperature of the air as it passes through the supercharger reduces the detonation margin. Steadily increasing manifold pressure (MaP) through supercharging will eventually bring about detonation, necessitating a lower compression ratio, higher-octane fuel, inter-cooling or methanol injection. Two-stage supercharging with intermediate cooling can raise the MaP and volumetric efficiency higher than a single-stage supercharger for the same detonation margin; and therefore greater power output and higher thermal efficiency.
- It is conceivable that single-stage supercharging could be employed with the cooling taking place after the supercharger but before the inlet manifold. However, intermediate cooling is attractive because the second stage of the supercharger doesn't have to work with such a high volume of air because the air is more dense following cooling at the end of the first stage.Dolphin (t) 11:42, 16 March 2015 (UTC)
What is the purpose of the section "Derivation of discrete formula" ?[edit]
In this long section, the relation between T and V for adiabatic heating and cooling is derived.
It seems that this derivation repeats much of the same work as was done to find the relation between P and V in a previous section. The new derivation uses the P-V relation, actually twice, and also the ideal gas law, as well as the fact that U is proportional to T, and in the end it seems somewhat circular.
Yet if one simply substitutes the ideal gas law in the P-V relation, the T-V derivation falls out immediately. I included this as a new section.
I don't see what the section entitled "Derivation of discrete formula" contributes. Shouldn't it be deleted?
89.217.4.12 (talk) 17:19, 14 March 2015 (UTC)
reason for edit[edit]
Here I have edited the first sentence of the lead, for the following reason.
The sentence that I overwrote was a near quote from a textbook that was cited, but the quote was misleading. The textbook, like most, was considering heat and work as an introduction to thermodynamics, without matter transfer. In particular, this text had written on its page 28: "In the rest of this chapter we shall confine our attention to systems consisting of specified matter, that is, to control masses. Energy, but not matter, can cross the boundary of such a system; the various mechanisms for this energy transfer are the main topic of this chapter." The sentence that I overwrote did not advise the reader of this presupposition of its definition, which was taken from page 48 of the text, some distance from the proviso of page 28.
The reader of the present Wikipedia article needs immediate and explicit notice that matter transfer is excluded from adiabatic transfer. Etymologically, adiabatic refers to passage without the explicit mention of heat or matter. Such exclusion of matter transfer is also left more or less implicit in most texts.
I did not retain the new citation because it is from a specialized, that is to say, engineering, text. Mostly, one does not put references in the lead, since the lead is largely an editorial summary. There are two references to the sentence that I put in, and they are sufficient, if not superfluous. They are to particularly important or authoritative sources.Chjoaygame (talk) 23:06, 23 October 2015 (UTC)
My putting into the first sentence of words to indicate that an adiabatic process is without matter transfer has been undone by Editor Zedshort. As to factuality, according to László Tisza "(adiabatic partitions inhibit the transfer of heat and mass)".[1]. The undoing edit summary says it was for simplicity. Texts normally precede their definitions of adiabaticity by general preliminary statements that they are referring to processes in closed systems, that is to say, without matter transfer. For Wikipedia to omit this customary preliminary would seem to be over-simplification.
Chjoaygame (talk) 08:45, 25 October 2015 (UTC)
Editor Zedshort has so far not responded to this section of the talk page. I wish to prevent editorial conflict, so I am here asking him please to respond here, unless he is happy to accept my edits without talk.Chjoaygame (talk) 21:37, 26 October 2015 (UTC)
It seems there is no response.Chjoaygame (talk) 23:56, 3 November 2015 (UTC)
reason for second edit[edit]
Here I have made a second edit. The reason is that the sentence that I overwrote uses a special terminology, "control-mass type of analysis", used for example in the particular textbook that was cited for it, but not defined in the present article and not widely standard in thermodynamics. Though it may have great merit, the special term is not needed for the present purpose.Chjoaygame (talk) 23:17, 23 October 2015 (UTC)
edits[edit]
Editor Zedshort has made two edits, here and here.
The first edit does not have an edit summary, no reason being given at that point for its change from
- An adiabatic process is one that occurs without transfer of heat or matter between a thermodynamic system and its surroundings; energy is transferred only as work.
into
- An adiabatic process is one that occurs without transfer of heat between a thermodynamic system and its surroundings. During an adiabatic process, energy is transferred only as work.
The substantial change made in this edit was to delete the usual statement on the adiabatic process, that it occurs in the absence of matter transfer.
The usual textbook account is in a chapter on closed systems, where closed systems are defined as those that do not transfer matter. It is not customary to repeat the definition of a closed system when the adiabatic process is being defined within a chapter on closed systems. It is usually left implicit as too obvious to need repetition. The newly edited version of the lead of present Wikipedia article gives the reader no notice of the key fact that that the adiabatic process is defined for a closed system. The result is that even as seasoned and much respected editor as Editor Dirac66 was able to express the possibility that perhaps it might be questioned whether an adiabatic process can include matter transfer, and asked for an explicit reference or two. So a new reader could be left in reasonable doubt. I provided an explicit reference, with an explicit verbatim quote "(adiabatic partitions inhibit the transfer of heat and mass)", in the body of the article, from Tisza, one of the very most careful and reliable authors on such questions. The explicit reference is given for the first sentence of the Description section of the article: "A process that does not involve the transfer of heat or matter into or out of a system, so that Q = 0, is called an adiabatic process, and such a system is said to be adiabatically isolated."[1] The fact is at least implicit in every definition of the term, and depending on the degree of directness demanded, not far from explicit. Editor Zedshort does not dispute it but seems to think it complicates things to make it explicit, when in his next edit summary, and in a previous edit summary for the same change, he writes "keep it simple".
The second edit has an edit summary that says "no reference provided, not expanded upon in the article, keep it simple". It deletes the last sentence of the first paragraph of the lead
- An adiabatic process is one that occurs without transfer of heat between a thermodynamic system and its surroundings. During an adiabatic process, energy is transferred only as work.[2][3]
The adiabatic process provides a rigorous conceptual basis for the theory used to expound the first law of thermodynamics, and as such it is a key concept in thermodynamics.
- An adiabatic process is one that occurs without transfer of heat between a thermodynamic system and its surroundings. During an adiabatic process, energy is transferred only as work.[2][3]
The article's first reference[2] for the second sentence is the classic source for the deleted sentence, and it is backed up by the article's second reference[3], which is a reliable survey published as a book, by the American Institute of Physics. Often detailed references are not demanded in the lead, but in this case they have been provided. If Editor Zedshort had read the references, and wanted references for the second sentence, he could have moved or repeated those for the first sentence.
- ^ Tisza, L. (1966). Generalized Thermodynamics, M.I.T Press, Cambridge MA: "(adiabatic partitions inhibit the transfer of heat and mass)", p. 48.
- ^ a b Carathéodory, C. (1909). Untersuchungen über die Grundlagen der Thermodynamik, Mathematische Annalen, 67: 355–386, doi:10.1007/BF01450409. A translation may be found here. Also a mostly reliable translation is to be found at Kestin, J. (1976). The Second Law of Thermodynamics, Dowden, Hutchinson & Ross, Stroudsburg PA.
- ^ a b Bailyn, M. (1994). A Survey of Thermodynamics, American Institute of Physics Press, New York, ISBN 0-88318-797-3, p. 21.
It is a reason for the theoretical importance of the adiabatic process that is expressed in the second sentence, the one that was deleted by the edit. It is true that it is not expanded upon in the body of the article. That could be remedied, if it should be thought in need of remedy, by a little commentary in the body of the article (now supplied), based on the first two references of the article, which are fully adequate for it. It does not improve the article instead to remove from the lead a statement of that important reason.Chjoaygame (talk) 00:30, 14 November 2015 (UTC)Chjoaygame (talk) 07:11, 14 November 2015 (UTC)
No response from Editor Zedshort!Chjoaygame (talk) 06:43, 20 November 2015 (UTC)
adiabatic walls do not allow transfer of matter[edit]
Editor Appleuseryu has edited here to say that adiabatic transfer can include matter transfer.
Because she seems new, I am not right now undoing his edit. But it needs to be undone. It is pretty routine to get just his edit. It has been discussed carefully in these talk pages. Most texts consider adiabatic processes within the context of closed (no matter transfer) systems. Adiabatic transfer usually crops up deep into those sections, out of sight of the introductory covering words 'closed system' and people can then forget that such is the context. They then jump to the conclusion that matter transfer is allowed. The texts are usually so sure of the context that they don't actually spell it out again for their treatment of adiabatic processes. For explicit words that say it, one can read <Tisza, L. (1966). Generalized Thermodynamics, M.I.T Press, Cambridge MA: "(adiabatic partitions inhibit the transfer of heat and mass)", p. 48.> and <Münster, A. (1970), Classical Thermodynamics, translated by E.S. Halberstadt, Wiley–Interscience, London, ISBN 0-471-62430-6, p. 48: "mass is an adiabatically inhibited variable."> These two are in the more reliable end of the reliable source spectrum.
To get past this, Editor Appleuseryu would need a strong case in reliable sources. I think that is not possible.
The best outcome is if Editor Appleuseryu undoes his own edit.Chjoaygame (talk) 17:01, 6 April 2016 (UTC)
- In short, I was wrong.
- I was thinking about the 'counter-example' of pomping airs into a container, which could be done adiabatically. However, it was incorrect of me to think of the system as the gas that is originally inside the bottle; one should also take consideration of the gas that is to be added.
- Appleuseryu (talk) 12:16, 8 April 2016 (UTC)
- Thank you for this comment. And thank you for your undo. Perhaps we can say that the entire system (the room and its contents) is adiabatically isolated (door shut tight, no windows) from the overall surroundings (the rest of the building and the surroundings), while its parts (the container, the rest of the room, the pump, and us) are not adiabatically isolated from each other? The process is transfer of air from the room into the container. It also includes work done on the pump which we may consider to come from the electric power mains, or from our mighty arms. One can set up the process in a diversity of ways.Chjoaygame (talk) 13:42, 8 April 2016 (UTC)
A remark on a terminological aspect: there is no such thing as matter transfer which would be improper naming, thus Wikipedia has an article called mass transfer. Heat and energy also belong to matter, there are no heat and energy outside the material world. We should use a consistent scientific language in scientific articles.--5.2.200.163 (talk) 12:31, 9 March 2017 (UTC)
ipa?[edit]
81.11.233.161 (talk) 22:08, 24 July 2016 (UTC)
Need a video[edit]
Need a video that can explain me the adiabatic process Nabeen369 (talk) 14:17, 22 November 2016 (UTC)
Error?[edit]
The following comment was posted by 49.199.220.64 about the section Adiabatic process#Example of adiabatic compression:
This has an error. The 10:1 compression ratio is the swept volume of the cylinder V1 -> V2, it is only effective to regard this as a reasonably true compression ratio in a near static laboratory model or extremely low speed engine, as the higher mean piston speed, the lower the effective fill of that cylinder i.e. 1/2 V1 = 1/2 V2. It leads onto this comment that is erronious: "That is a final temperature of 753 K, or 479 °C, or 896 °F, well above the ignition point of many fuels. This is why a high-compression engine requires fuels specially formulated to not self-ignite (which would cause engine knocking when operated under these conditions of temperature and pressure)," I think the maximum TRUE compression ratio can not exceed in a final air temperature of ~180 to 220*C - depending on the fuel or fuel blend low, medium and high octane number fuels, such as unleaded 82 octane or high octane fuels such as alcohol or alcohol / water / high octane petrol / blends. Hence the error with regarding 10:1 compression, as distinct from the compression ratio as a fact, in a high speed petrol engine.
(Please direct comments about this to the IP, not me.) --JBL (talk) 13:03, 2 December 2017 (UTC)
Need Example: Fire piston[edit]
This is a practical example where a rapid decrease in volume results in a rapid increase in both temperature and pressure. Not sure how the increases are partitioned (between temperature and pressure) but it sets things on fire. Whether the example goes here, or in fire piston with a reference back here is what I don't know.
Riventree (talk) 19:45, 22 June 2019 (UTC)
- I suggest you add Fire piston to Adiabatic process#See also. Dolphin (t) 00:51, 23 June 2019 (UTC)
Set theory and the adiabatic process / adiabatic evolution/decay/filtering[edit]
These is the theory of the entropic sets; you use mathematical filters in order to express the decay of each set to a more decayed one. There are issues because: 1. not all subsets decay at the same pace, 2. at periodical orders of hyperset / grouping magnitude we have a reaction as a whole.
We have to express the adiabatic decay of a region of a pretopological space; which occurs under specific conditions (it doesn't happen at any condition).
Sets which are able to decay, using filter-logic (mathematical logic using rules of mathematical filters), are extremely important in order to understand complex systems which aren't static.
Humanity has been lazy on the topic, but few links exist.
make page: Filter logic Which means: sets which evolve via the application of logical operations based on the rules of some ±mathematical filters (different per case).
After we write that; we then can write the adiabatic evolution of some sets, as a sub-case. We cannot start from Z (the conclusion) if we don't write A (the basics). — Preceding unsigned comment added by 2A02:587:4112:2F00:4005:4380:AB99:AB8C (talk) 20:51, 19 July 2019 (UTC)
- Artificial neural networks are useful to be used in order to describe the points of a set; but we should start simple. If you immediately add everything it doesn't work. Gradually you add components to the theory; iff are useful. — Preceding unsigned comment added by 2A02:587:4112:2F00:4005:4380:AB99:AB8C (talk) 20:59, 19 July 2019 (UTC)
P-V plot size[edit]
I was trying to improve the P-V plot in the article, but I think I messed up the size somehow and it seems terribly out of proportion now. Halp? [Above edit 26 July 2019 by PlasmaPerfi as per edit history.] — Preceding unsigned comment added by PlasmaPerfi (talk • contribs)
- This seems to refer to the section Graphing adiabats. You did not specify an image size so the system used the default which seems to be enormous. I have now arbitrarily added 400 px (pixel) which appears much more reasonable. Dirac66 (talk) 21:23, 26 July 2019 (UTC)
- The "image" link is deprecated, so when the image size change the behavior was unexpected. Use "file" instead. Not your fault, PlasmaPerfi; thanks for updating the image on Commons! VQuakr (talk) 21:25, 26 July 2019 (UTC)
Too academic[edit]
This article is very academic. Some practical examples would help readers understand the process. FreeFlow99 (talk) 14:57, 20 June 2020 (UTC)
"Various applications of the adiabatic assumption" needs work[edit]
- these seem to be a list of thermodynamic facts for situations which are a mix of adiabatic and non-adiabatic processes.
- the first and last bullets are examples that are non-adiabatic, so not really applications of the adiabatic assumption.
- terms are used before being defined - e.g. isochoric in the second bullet.
- overall the section reads like it was transcribed from a different context.
Impossible process?[edit]
"Energy can enter or leave a thermodynamic system enclosed by walls that prevent mass transfer only as heat or work. Therefore, a quantity of work in such a system can be related almost directly to an equivalent quantity of heat in a cycle of two limbs. The first limb is an isochoric adiabatic work process increasing the system's internal energy; the second, an isochoric and workless heat transfer returning the system to its original state."
So the first process is: 1. isochoric, meaning no pV work done on the system, and 2. adiabatic, meaning no heat transfer into the system. Considering the system is also stated to be closed, how can it's internal energy possibly increase with a process like this? Erjio (talk) 22:56, 22 September 2023 (UTC)
- C-Class vital articles
- Wikipedia level-5 vital articles
- Wikipedia vital articles in Physical sciences
- C-Class level-5 vital articles
- Wikipedia level-5 vital articles in Physical sciences
- C-Class vital articles in Physical sciences
- C-Class physics articles
- Mid-importance physics articles
- C-Class physics articles of Mid-importance
- Etymology Task Force etymologies
- C-Class Weather articles
- Mid-importance Weather articles
- C-Class General meteorology articles
- Mid-importance General meteorology articles
- WikiProject Weather articles









